What is the role of the first “random” layer in the Rosenblatt perceptron
So in the Rosenblatt Perceptron article - what is forgotten and invented by history? in principle, as expected, some lack of awareness about the essence of the Rosenblatt perceptron (someone has more, someone less) has surfaced. But honestly, I thought it would be worse. Therefore, for those who know how and want to listen, I promised to write how it turns out that random connections in the first layer perform such a difficult task of mapping an inseparable (linearly separable) representation of the problem into a separable (linearly separable).
Honestly, I could just refer to the Rosenblatt convergence theorem, but since I don’t like it when I am “sent to Google,” let's understand. But I proceed from the fact that you know from the originals what the Rosenblatt perceptron is (although understanding problems have surfaced, but I still hope that only individuals have it).
Let's start with the materiel.
So, the first thing we need to know is what is the A-matrix of the perceptron and G-matrix of the perceptron. I’ll give you links to Wikipedia, I wrote myself so you can trust (directly from the original):
1. A perceptron A-matrix
2. Perceptron G-matrix , here you need to pay attention to the Relationship between A and G - perceptron matrices
whoever does not master this, please do not read further, close the article and smoke - this article is not for you. Do not rush, not everything at once in life becomes clear, it also took me a couple of years to study the nuances of the perceptron. Read here a little - do experiments.
Next, let's talk about the theory of convergence of the perceptron. They talk a lot about her, but I'm sure 50% have not seen her in the eye.
So, from one of my scientific articles:
I will not naturally consider the evidence (see the original), but what will be important to us next is that the convergence of the perceptron is not mathematically guaranteed (it is not guaranteed it doesn’t mean it will not - with simple input data it will, even if it is violated, we are talking about arbitrary input data) in two cases:
1. If the number of examples in the training set is greater than the number of neurons in the middle layer (A-elements)
2. If the G matrix has determinants equal to zero
According to the first part, everything is simple, we can always set the number of A-elements equal approximately in in the training set.
But the second part is especially interesting in the light of our question. If you have mastered the understanding of what kind of G-matrix it is, then it is clear that it depends on the input data and what kind of connections formedrandomly in the first layer.
And now we get to the question:
The probability of activity of A - elements
Further, I will skip the details a bit and immediately give a drawing:
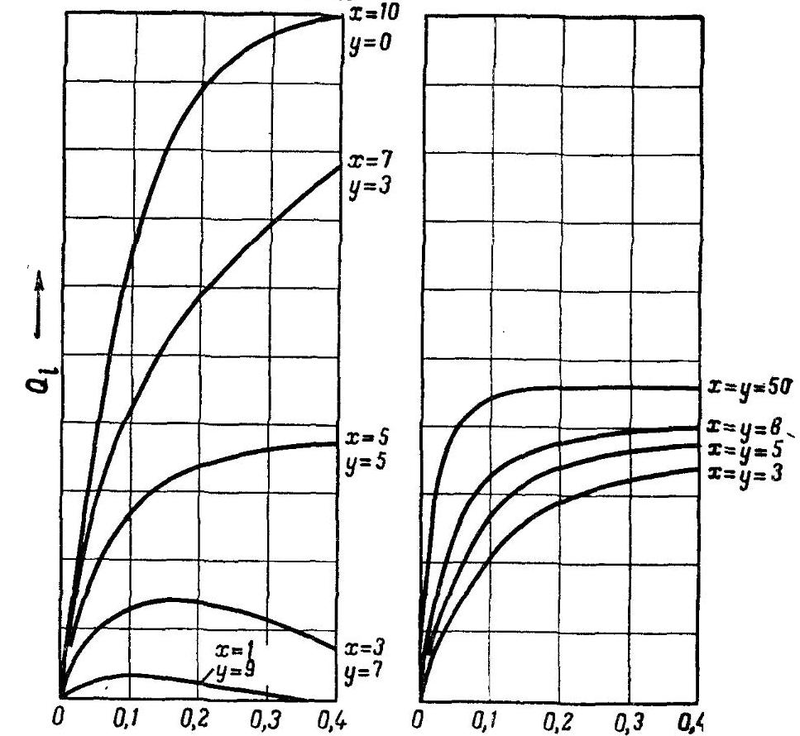
this is the so-called. Q-functions analyzed by Rosenblatt. I will not go into details, but it is important that:
x is the number of exciting bonds in the first layer, suitable for one A-element (weight +1) and y is the number of inhibitory bonds (weight -1). The y-axis in the figure shows the magnitude of this Q-function, which depends on the relative number of illuminated elements on the retina (1 at the input).
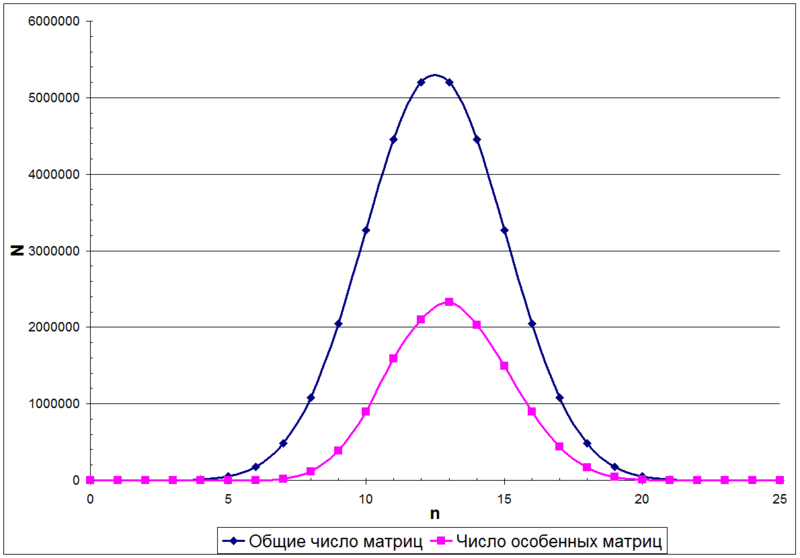
In this case, the number of units in matrix A will be described by a binomial distribution. For example, the following figure shows the distribution of the number of matrices N depending on the number of units n in a 5 × 5 matrix.
Finally, what is the probability that A is special?
And this is what can be seen in the following figure (these are the probabilities of the appearance of non- special matrices depending on their size):
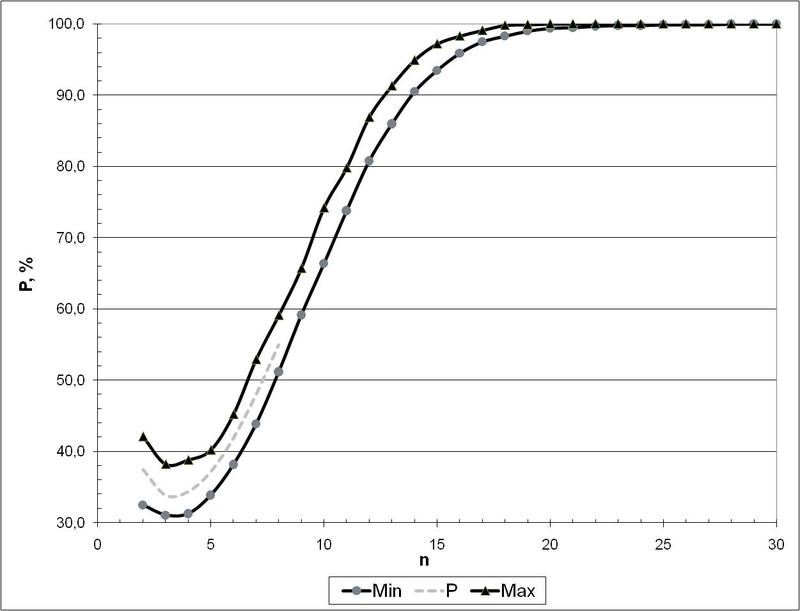
So, from here it can be seen that even with a matrix size of 30 x 30 (i.e. when the number of A-elements is 30 or more), talk about almost 100% confidence that a randomly obtained matrix will not be special. This is the final practical condition under which the Rosenblatt perceptron will form a space that satisfies the compactness hypothesis. In practice, it is more reliable to have a minimum of about 100 A-elements to exclude the case when the G-matrix becomes special.
In conclusion.Now ask yourself: is MLP + BackProp guaranteed, what have I described to you here regarding the Rosenblatt perceptron? I did not find convincing evidence for this anywhere (just do not throw links to the mat. Evidence of convergence of gradient descent - this does not apply to this, I advise my opponents best to write their intelligible article on this subject: “ thoughts from one’s head are welcomed in Habrahabr ” more constructive). But based on the problem of getting into local minima when using BackProp, it seems that not everything is clean and smooth, as with the Rosenblatt perceptron.
upd. that I somewhat overlooked in the presentation, and during the dialogue we clarified here. Thanks to retran and justserega for leading questions.
Summary. Corollaries 1 and 2 say that under certain conditions a solution is impossible. Here I proved that such conditions do not occur at n> 30 (Rosenblatt did not do this). But readers had two questions
1. Well, the A-matrix (and, through it, G) is suitable with high probability. But how does this help move to another space? . Indeed, not very obvious. I explain. The A-matrix is the “other space” - the space of features. The fact that the matrix is not special and this matrix is one dimension larger than the original one is a sign that it can be divided linearly. (this follows from the corollaries and Theorem 3)
2. " Is there evidence that the error correction algorithm in the Rosenblatt perceptron will converge?"Indeed, Theorem No. 3 only says that a solution exists. This already means that this solution exists in the attribute space, that is, after the random first layer has worked. The error correction algorithm trains the second layer, and exists with Rosenblatt Theorem No. 4, in which he proves that the existing possible solutions (Theorem 3, that they even exist) can be achieved precisely by applying the learning algorithm with error correction.
Another important point follows from the fact that the A-matrix depends on the input data on the one hand and, on the other hand, on a random matrix of connections. More precisely, the input matrix is mapped to matrix A through a random operator (randomly formed bonds). If we introduce a measure of randomness, such as the rate of occurrence of subsequences that will be repeated (pseudo-randomness), then it turns out: (1) if it is not random at all, but an operator constructed according to some rules (i.e., joining the first layer), then the probability of getting A significantly increases -special matrix (2) if, after multiplying the input matrix by the pseudo-randomness obtained by us, the A-matrix has not a regular, but a random spread of units (let's call this condition R), then this is exactly what we analyzed in the article above.
Here I will reveal to you my tested thing. According to the idea of a binomial model of randomness when creating connections (this is when an A element is taken and N exciting and M inhibitory connections to S elements are randomly drawn from it) it is enough to fulfill condition R. But to speed up the convergence process, you can get a greater level of chaos in matrix A. How to do this - cryptography just tells us. Here is such a connection with cryptography here is still drawn.
Honestly, I could just refer to the Rosenblatt convergence theorem, but since I don’t like it when I am “sent to Google,” let's understand. But I proceed from the fact that you know from the originals what the Rosenblatt perceptron is (although understanding problems have surfaced, but I still hope that only individuals have it).
Let's start with the materiel.
So, the first thing we need to know is what is the A-matrix of the perceptron and G-matrix of the perceptron. I’ll give you links to Wikipedia, I wrote myself so you can trust (directly from the original):
1. A perceptron A-matrix
2. Perceptron G-matrix , here you need to pay attention to the Relationship between A and G - perceptron matrices
whoever does not master this, please do not read further, close the article and smoke - this article is not for you. Do not rush, not everything at once in life becomes clear, it also took me a couple of years to study the nuances of the perceptron. Read here a little - do experiments.
Next, let's talk about the theory of convergence of the perceptron. They talk a lot about her, but I'm sure 50% have not seen her in the eye.
So, from one of my scientific articles:
: The following theorem proved
'' 'Theorem 3.' The letter elemental perceptron space stimuli W and some classification C (W). Then for the existence of the solution it is necessary and sufficient that there exists some vector u lying in the same orthant as C (W) and some vector x such that Gx = u. ”
as well as two direct corollaries from this theorem:
“Corollary 1.” An elementary perceptron and stimulus space W are given. Then, if G is a singular matrix (whose determinant is zero), then there is some classification C (W) for which there is no solution. ”
“” “Corollary 2.” “If the number of stimuli in the space W is greater than the number A of elements of the elementary perceptron, then there is some classification C (W) for which there is no solution.”
Rosenblatt calls the stimulus space the source data space.
I will not naturally consider the evidence (see the original), but what will be important to us next is that the convergence of the perceptron is not mathematically guaranteed (it is not guaranteed it doesn’t mean it will not - with simple input data it will, even if it is violated, we are talking about arbitrary input data) in two cases:
1. If the number of examples in the training set is greater than the number of neurons in the middle layer (A-elements)
2. If the G matrix has determinants equal to zero
According to the first part, everything is simple, we can always set the number of A-elements equal approximately in in the training set.
But the second part is especially interesting in the light of our question. If you have mastered the understanding of what kind of G-matrix it is, then it is clear that it depends on the input data and what kind of connections formedrandomly in the first layer.
And now we get to the question:
But since the first layer of bonds in the perceptron is randomly selected and not trained, it is often believed that with equal probability the perceptron may work or may not work with linearly inseparable input data, and only linear input data guarantee its perfect operation. In other words, - the perceptron matrix with equal probability can be both special and not special. It will be shown here that such an opinion is erroneous. (hereinafter, quotes from my scientific articles)
The probability of activity of A - elements
From the definition of matrix A we see that it is binary, and takes the value 1 when the corresponding A - element is active. We will be interested in what is the probability of a unit appearing in the matrix and, accordingly, what is the probability of zero.
Further, I will skip the details a bit and immediately give a drawing:

this is the so-called. Q-functions analyzed by Rosenblatt. I will not go into details, but it is important that:
x is the number of exciting bonds in the first layer, suitable for one A-element (weight +1) and y is the number of inhibitory bonds (weight -1). The y-axis in the figure shows the magnitude of this Q-function, which depends on the relative number of illuminated elements on the retina (1 at the input).
The figure shows the dependence of the probability of activity of A - element Qi on the magnitude of the illuminated area of the retina. Note that for models that have only exciting connections (y = 0) with a high number of illuminated S - elements, the value of Qi approaches 1. That is, the probability of activity of A - elements is directly dependent on the number of illuminated S - elements, which is bad affects the recognition of relatively small and large images. As will be shown below, this is due to the high probability that the A - matrix will be special. Therefore, for the stability of pattern recognition of any geometrical dimensions, it is necessary to choose the x: y ratio so that the probability of activity of A - elements as little as possible depends on the number of illuminated S-elements.
... it can be seen that at x = y the value of Qi remains approximately constant in the entire region, with the exception of a very small or very large number of illuminated S - elements. And if you increase the total number of bonds, the region in which Qi remains constant, expands. At a small threshold and equal to x and y, it approaches 0.5, i.e. It is equal to the probable occurrence of activity of A - element on an arbitrary stimulus . Thus, conditions are found under which the appearance of unity and zero in matrix A is equally probable.
In this case, the number of units in matrix A will be described by a binomial distribution. For example, the following figure shows the distribution of the number of matrices N depending on the number of units n in a 5 × 5 matrix.

Finally, what is the probability that A is special?
From the binomial distribution, you can find out how the total number of matrices with a different number of units in the matrix is distributed (the upper curve in the previous figure). But for the number of nonsingular matrices (lower curve in the previous figure), a mathematical formula does not currently exist.
But there is a sequence A055165 [6], which gives the probability of precisely the fact that a matrix of size nxn is not special. But it can be counted only by exhaustive search and this is done before the cases n <= 8. But subsequent values can be obtained by the Monte Carlo method ...
And this is what can be seen in the following figure (these are the probabilities of the appearance of non- special matrices depending on their size):

So, from here it can be seen that even with a matrix size of 30 x 30 (i.e. when the number of A-elements is 30 or more), talk about almost 100% confidence that a randomly obtained matrix will not be special. This is the final practical condition under which the Rosenblatt perceptron will form a space that satisfies the compactness hypothesis. In practice, it is more reliable to have a minimum of about 100 A-elements to exclude the case when the G-matrix becomes special.
In conclusion.Now ask yourself: is MLP + BackProp guaranteed, what have I described to you here regarding the Rosenblatt perceptron? I did not find convincing evidence for this anywhere (just do not throw links to the mat. Evidence of convergence of gradient descent - this does not apply to this, I advise my opponents best to write their intelligible article on this subject: “ thoughts from one’s head are welcomed in Habrahabr ” more constructive). But based on the problem of getting into local minima when using BackProp, it seems that not everything is clean and smooth, as with the Rosenblatt perceptron.
upd. that I somewhat overlooked in the presentation, and during the dialogue we clarified here. Thanks to retran and justserega for leading questions.
Summary. Corollaries 1 and 2 say that under certain conditions a solution is impossible. Here I proved that such conditions do not occur at n> 30 (Rosenblatt did not do this). But readers had two questions
1. Well, the A-matrix (and, through it, G) is suitable with high probability. But how does this help move to another space? . Indeed, not very obvious. I explain. The A-matrix is the “other space” - the space of features. The fact that the matrix is not special and this matrix is one dimension larger than the original one is a sign that it can be divided linearly. (this follows from the corollaries and Theorem 3)
2. " Is there evidence that the error correction algorithm in the Rosenblatt perceptron will converge?"Indeed, Theorem No. 3 only says that a solution exists. This already means that this solution exists in the attribute space, that is, after the random first layer has worked. The error correction algorithm trains the second layer, and exists with Rosenblatt Theorem No. 4, in which he proves that the existing possible solutions (Theorem 3, that they even exist) can be achieved precisely by applying the learning algorithm with error correction.
Another important point follows from the fact that the A-matrix depends on the input data on the one hand and, on the other hand, on a random matrix of connections. More precisely, the input matrix is mapped to matrix A through a random operator (randomly formed bonds). If we introduce a measure of randomness, such as the rate of occurrence of subsequences that will be repeated (pseudo-randomness), then it turns out: (1) if it is not random at all, but an operator constructed according to some rules (i.e., joining the first layer), then the probability of getting A significantly increases -special matrix (2) if, after multiplying the input matrix by the pseudo-randomness obtained by us, the A-matrix has not a regular, but a random spread of units (let's call this condition R), then this is exactly what we analyzed in the article above.
Here I will reveal to you my tested thing. According to the idea of a binomial model of randomness when creating connections (this is when an A element is taken and N exciting and M inhibitory connections to S elements are randomly drawn from it) it is enough to fulfill condition R. But to speed up the convergence process, you can get a greater level of chaos in matrix A. How to do this - cryptography just tells us. Here is such a connection with cryptography here is still drawn.
