When discussing the structure of an atom and a substance, one can often read that a substance at 99.99 ...% consists of emptiness, with different versions of the number of nines. As we shall see, this statement has very tenuous grounds, and attempts to estimate the fraction of voids in a substance can give with equal success any number from 0 to 100%. Consecutive consideration of the issue within the framework of quantum mechanics shows that matter differs quite strongly from emptiness.

What is wrong with 99%?

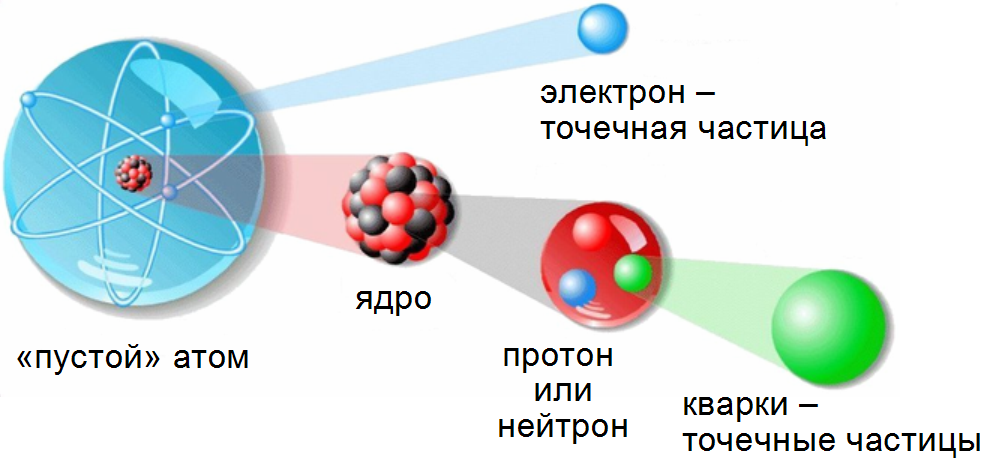
Traditional line of reasoning^(*) looks like this: in an atom having a size of about one angstrom ( ^10–10 meters), electrons rotate around a nucleus, the size of which is 100,000 times smaller (about ^10–15 meters). The size of the electron itself is zero, it is a point particle.^(**) , therefore, the atom turns out to be practically empty: there is only a “non-empty” nucleus in it. To get the fraction of the volume of an atom occupied by the nucleus, it is necessary to cube the ratio of their sizes. We get that the nucleus occupies ^10–15 volumes of an atom, the remaining volume share is 99.99 ...% with 13 nine decimal places - it takes up emptiness.


If the atom is stretched to the size of a football field, the core will be as large as a poppy seed.

What is wrong with this reasoning? Let's continue the same logic, considering not the atom, but its core. We considered the atomic nucleus to be non-empty, but it consists of protons and neutrons, which, in turn, consist of fundamental particles - quarks and gluons^(***) . According to modern concepts, quarks and gluons are alsopoint particles, like an electron. Following the same line of reasoning as in the case of an atom, we find that the nucleus is also a void in which particles of zero size fly. Bottom line: the substance is exactly 100% composed of emptiness. This line of reasoning led us nowhere.

What does quantum mechanics say?

Quantum mechanics tells us that an electron in an atom is not a small ball flying in orbit around a nucleus, but smeared in space in the form of a probabilistic cloud called an orbital. The density of this cloud, or just electron density$$depends on the coordinates $$. This dependence is different for each orbitals, however, there is a general pattern:$$ noticeably different from zero in the region of space with dimensions of the order of angstrom, and exponentially decreases at large distances from the nucleus.


Typical behavior of electron density in an atom for different electron orbitals. Source .

Hence the characteristic size of an atom in one angstrom, used above when comparing the size of an atom and a nucleus. What is the quantitative answer to the question of the fraction of voids in a substance can quantum quantum mechanics give us? For this, it is necessary to estimate the total volume occupied by the electron orbitals of all atoms. And for this, in turn, a clear boundary should be drawn between the atom and the surrounding voidness. But how to do that? Formally, electron density$$, although it tends to zero with distance from the nucleus, it never turns to zero, therefore each atomic orbital fills, if not the whole Universe, then at least the entire volume of the considered piece of matter. In this case, it turns out that there is no void in the substance - at any point there is a nonzero probability to find an electron.

You can define the boundary of the atom as a place where the electron density reaches 1/2 of the maximum. Or 1/15 - such a border will be farther from the core. Or as a surface, inside which 1/2 all the total electron density is contained. You can grab more volume by swiping a surface into which, for example, 9/10 of the entire density falls.


Electron Cloud Density for Orbitals $$in the hydrogen atom (shown in white) and different options for the conditional boundary of the atom.

As you can see, by conducting the atomic boundaries of atoms in different ways, one can get different values ​​of the volume they occupy. Therefore, for the proportion of voids in the substance, you can get any answer from 0 to 100%. For example, in this video, the proportion of voids is estimated at 90%. Why precisely 90, not 80 or 95? Apparently, the author took some kind of "standard" atom size in the region of one angstrom.

Although they are not suitable for accurately determining the boundaries of an atom of a surface of equal electron density, they are convenient when it is necessary to visually depict the structure of matter at the micro level. The shape of these surfaces can be judged on the structure of molecular orbitals and chemical bonds.


An example of a surface (it is green and translucent) on which the electron density in a crystal takes a constant value. Source .


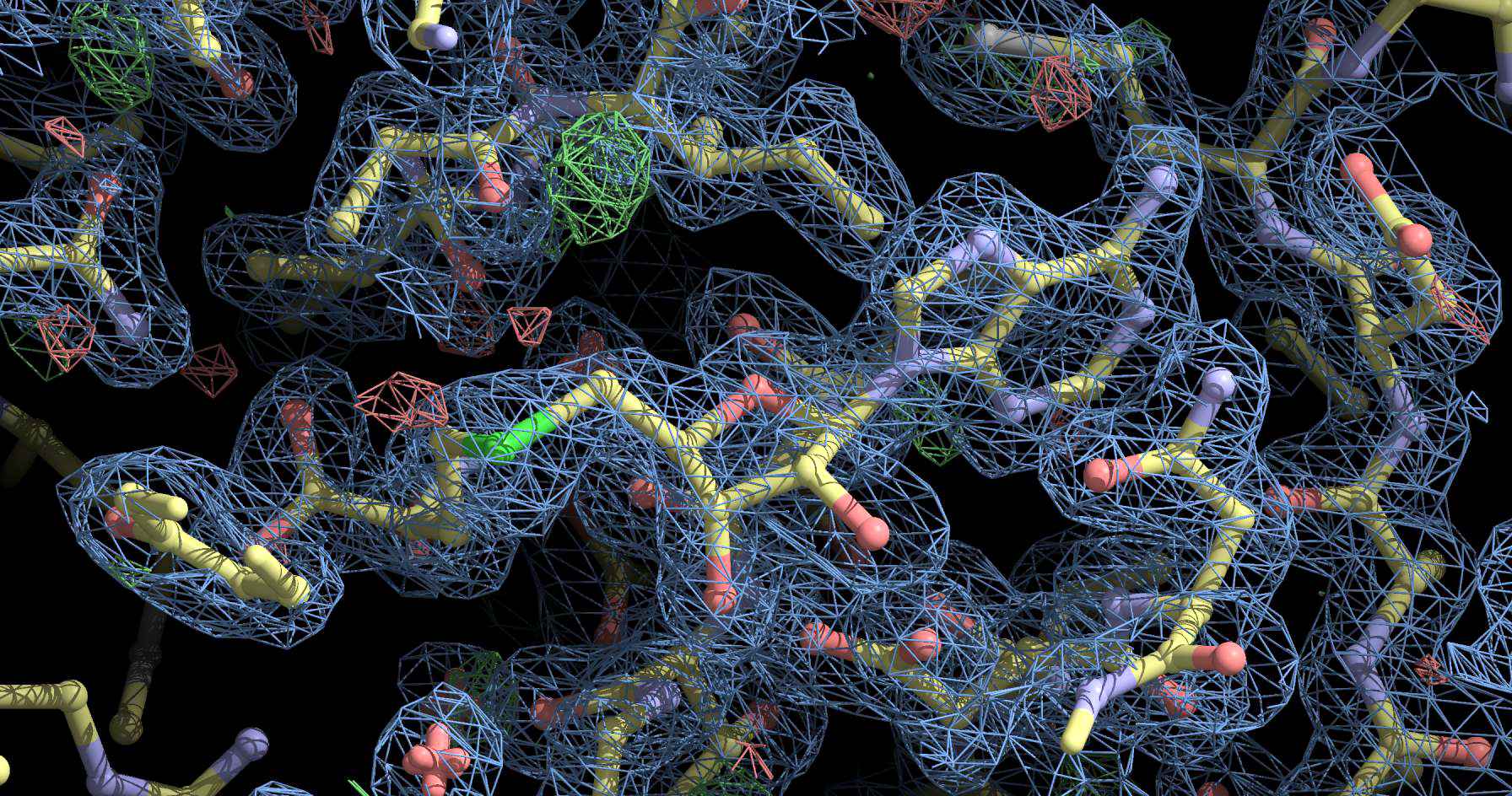
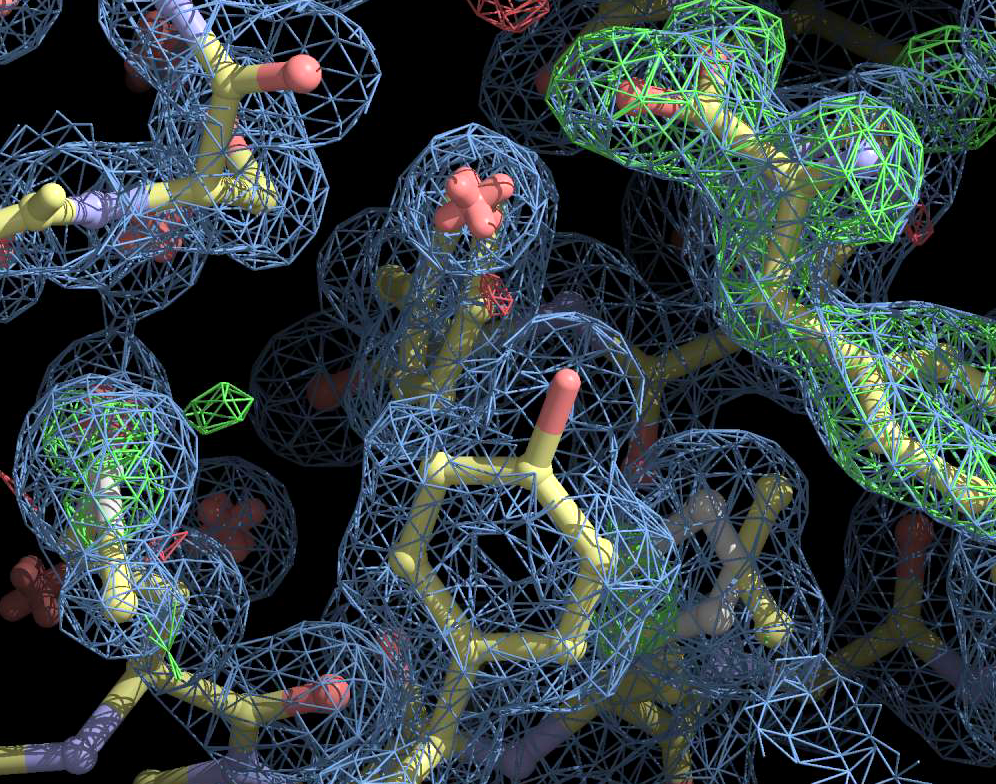
And this is how the surfaces of constant density look like in some proteins. Source .

What does quantum field theory say?

Even if substance cannot be clearly separated from emptiness, is it possible at least to answer the question, what in general, from the point of view of quantum theory, does matter differ from empty space? To answer, we turn to quantum field theory, which studies the systems of many particles and vacuum. In this theory, any state of the system (more precisely, a quantized field) in which there can be 0, 1, 2, etc. particles, characterized by a vector whose length is equal to one.


If there is not a single particle (void) in the system, its state is called vacuum, and the corresponding vector is usually denoted as $$. An atom with one electron on any orbital is the state of a system with one particle, the vector of which can be designated as$$. How different are these two states from each other? There are different ways to describe the "distance" between vectors, the most simple and often used^(****) - calculate the length of the difference of the vectors$$. It can be shown that vectors$$ and $$mutually perpendicular, this is a common situation for essentially different quantum states. It turns out that, from the point of view of quantum field theory, the "distance" between a void and an electron located in the atomic orbital is$$.


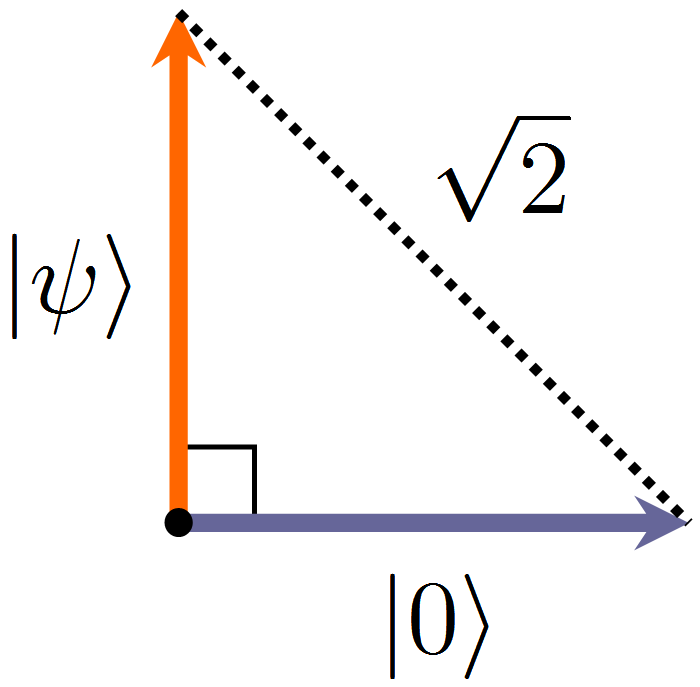
Two mutually perpendicular state vectors - vacuum and one electron in the atomic orbital - and the distance between them.

The resulting answer - that matter is always radically different from emptiness, even if it contains one particle per cubic kilometer - is not very satisfactory, because the distribution of matter in space completely falls out of it. Is it possible to introduce a measure of the difference of a substance from a void, showing how much they differ not as a whole, but locally, at each point$$? Yes, such a measure can be found, and it is nothing more than electron density.$$. Where the electron density falls to extremely small values, the difference between matter and void also becomes insignificant.




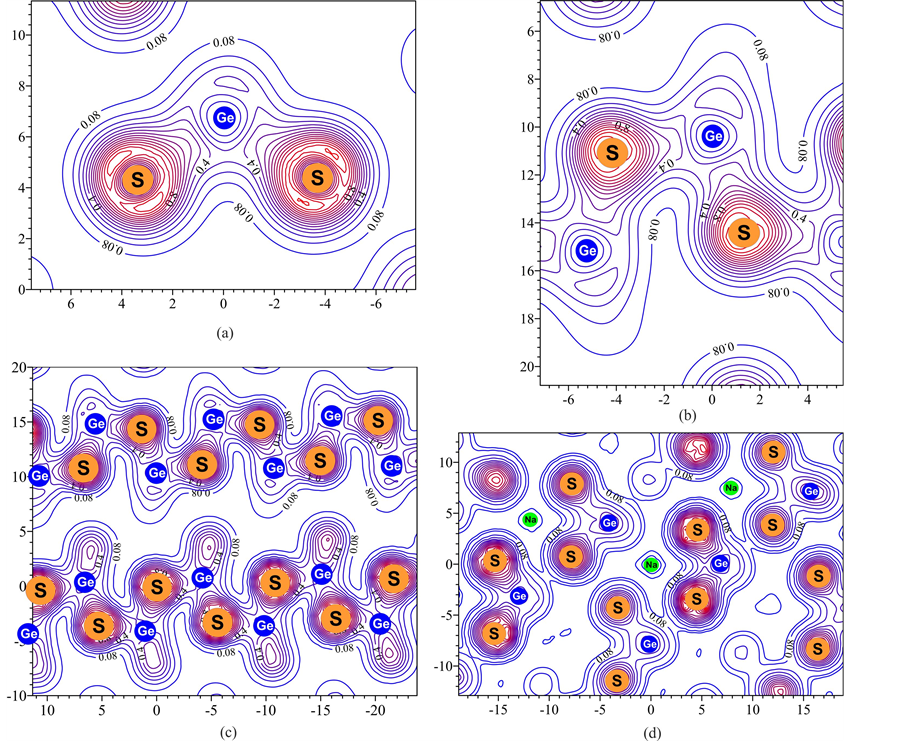
Lines of equal electron densities in a Na ₂ GeS ₃ crystal . The farther from the atomic nuclei, the lower the density, and the closer the void. Source .

So, we see that:

• If you argue in the spirit of “only a nucleus is non-empty in an atom”, then you will have to admit that the substance is exactly 100% empty , because the nucleus is an empty “atom” just made up of other particles.
• In quantum mechanics, the electron shells of atoms are smeared in space, and it is impossible to say exactly where the atom ends and the empty space surrounding it begins. As a result, it is impossible to say exactly what the proportion of voids in a substance is - with the same success, you can take any number from 0 to 100% .
• From the point of view of quantum field theory, matter with even one electron is significantly different from vacuum - these two quantum states are represented by mutually perpendicular vectors, the distance between which is $$.
• However, it is possible, in a sense, to introduce a measure of the difference between a substance and a vacuum not locally, but locally, at every point in space. This measure is electron density.$$. Unfortunately, electron density is a dimensional quantity, it has a dimension of m ^–3 , and therefore does not give us an answer to the question “by how many percent does matter at this point differ from emptiness”. With its help, you can only judge where the substance is more different from the void, and where it is weaker. Near the centers of atoms$$ maximum, there the substance differs from emptiness most strongly, and at large distances from atoms it decreases very quickly, and the difference between matter and emptiness becomes insignificant.

^(*) Here are examples of this kind of reasoning, in which, however, the ratio of the size of an atom and the nucleus is sometimes exaggerated millions of times:
• www.popmech.ru/science/10566-zhiznn-v-pustote-kvantovoe-osoznanie
• www.yaplakal. com / forum7 / topic1503279.html
• pikabu.ru/story/tyi_nichto_561687
• thequestion.ru/questions/10102/atom-sostoit-iz-pustoty-vsyo-materialnoe-sostoit-iz-atomov-kak-materialnoe-mozhet-sostotost iz-pustoty

^(**) At least, experiments at the Large Electron-Positron Collider showed that the electron size does not exceed ^10–19 m. Later, ultra-precise measurements of the electron magnetic moment gave an upper estimate of the electron size equal to 10 ^–20 m. These estimates show that the electron is at least tens of thousands of times smaller than the nucleus.

^(***) Interesting fact: the three quarks that make up the proton give only less than 2% of its mass. The rest of the mass is virtual particles (quarks and gluons), resulting from the interaction of the three original quarks. There are so many of these particles that they form a whole “sea”, and therefore are called “sea” quarks and gluons.

^(****) In the case of two pure quantum states$$ and $$such measures of the distance between them, as the Hilbert-Schmidt metric and the Fubini-Study metric , reduce precisely to the length of the vector$$.