About two-dimensional packaging: offline algorithms
Today, dear Habr, I will tell you a story about combinatorial optimization.
From ancient times (at least from the beginning of the last century), mathematicians wondered how to optimally place a certain amount ofbeer of necessary and useful objects in a backpack. The task of the knapsack and its subtasks was formulated - thousands of them! - which interested computer scientists, cryptographers and even linguists.
The task of packing in containers ( Bin Packing Problem), one of the varieties of which is the problem of two-dimensional packaging (2-Dimensional Bin Packing). Having discarded several variations again, we finally come to two-dimensional packing in a semi-limited strip (2-Dimensional Strip Packing, 2DSP). Feel how much interesting is already behind the scenes? But we have not finished wading through the classification. 2DSP has two input options: when the set of packed objects is known in advance (offline problem) and when the data arrives in batches (online problem).
This article discusses algorithms for solving offline-variant 2DSP. Under the cut, there is a bit of materiel and a lot of pictures with colored squares.
As a special case of the two-dimensional packing problem, 2DSP consists in packing objects of a particular shape into a finite number of containers of a particular shape in such a way that the number of containers used is the smallest or the number or volume of objects (which pack) are the largest. The difference with two-dimensional packaging is that there is only one container, and instead of minimizing the number of containers, we minimize the height of one. We provide maximum packing density if you want.
Since the problem is NP-hard, research focuses mainly on developing approximate solution algorithms. (The genetic algorithm was mentioned on Habré) Approximate algorithms find the optimal solution with a certain accuracy, but do not guarantee optimal packaging for any data set. In this case, the criterion of optimality depends on what you tried to optimize.
I’ll talk about the simplest strategies and what it all applies to in life (except for a backpack with beer).
So, we have a set of n rectangles and a semi-limited container-glass with a fixed width W and infinite height. Each rectangle does not exceed W in width. The task is to put the rectangles in the glass without overlapping and intersecting so that the glass becomes as small as possible. Let's agree that all rectangles should be packed orthogonally, they cannot be rotated.
It can be seen that the problem has an ideal solution in which the height of the packed rectangles is equal to their total area divided by the width of the strip.
For the offline version of 2DSP, the size of all the packed rectangles is immediately known, so they can be sorted, selected according to a specific criterion, grouped or simply bumped into suitable places. Most algorithms are based on this:
Flat algorithms place rectangles strictly close to each other, but this is not the most successful strategy, as it might seem at first glance. Level ones divide the strip into levels equal in height to one of the selected rectangles, and put all the others on a specific level according to a certain criterion. Shelf shelves predetermine several shelves (shelves) at once, and push rectangles along them, this behavior is typical for online-algorithms, and this is a completely different story.
Than to extend to common words, it is better about everything in order.
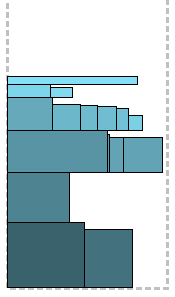
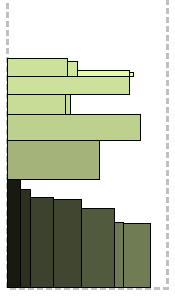
The algorithm, as they say, "in the forehead." Rectangles are sorted by non-increasing height (Decreasing High hints), the highest is located in the lower left corner of the strip, thereby initializing the first level equal in height to it. The remaining rectangles are located from left to right, while there is space at the current level. A rectangle that does not fit on a level is placed on top to form the next level, and so on.
Illustrations for each algorithm will be made for the following two examples: for clarity, in the left, the shape of the rectangles tends to be elongated, in the right - more square.
NFDH Algorithm
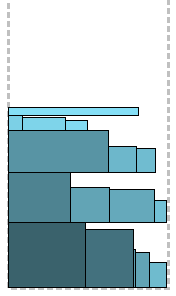
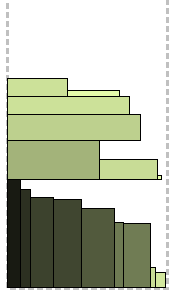
Similar to the previous algorithm, with the difference that for each next rectangle a place is sought not only at the last level, but starting from the lowest. Hence the “first fit” - the rectangle is placed on the first suitable level from below. Intuitively, the packaging will be better. Another significant difference is in performance, since in the worst case, you will have to consider all levels from the bottom up at every step.
FFDH Algorithm

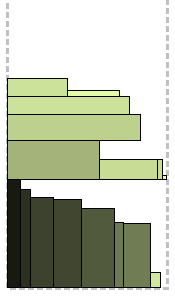
Modification of the previous algorithm. Its essence is that of the levels suitable for packing the next rectangle, not the first, but the best one is chosen. The best level is one where there will be a minimum of space after packing the current rectangle. Simply put, the minimum suitable space is chosen, which contributes to a better filling of the levels.
BFDH Algorithm

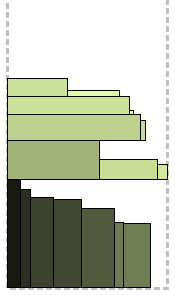
It is worth staying in more detail. Knapsack 0-1 is a special case of the knapsack problem; It is noteworthy that in addition to answering the main question (no, not 42, but the resulting packaging volume) it also gives a solution - a list of items that need to be packaged. The procedure is as follows: rectangles are sorted by non-increasing height; the first rectangle is packed to a new level; for this level there is a solution to the Knapsack 0-1 problem, which gives us a list of rectangles maximized in area. The selected rectangles are packed and retrieved from the unpacked list, the level closes and a new one opens - initialized, as usual, the first (highest) of the remaining ones. Repeat until there are rectangles.
Algorithm KP01
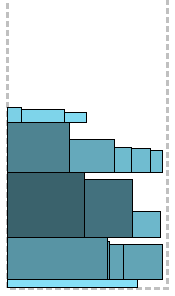

Algorithm designed to improve FFDN on the principle of "divide and conquer." First, rectangles that are wider than half the strip are selected. They will be packed first. Of these, even wider ones are chosen — wider than 2/3 of the strip; they are packed with the FFDH algorithm. Above them, starting at the next level(let's call it level R), the remaining ones are packed, those that are still wider than 1/2, but already 2/3. They are also packaged using FFDH. This separation creates a free region with a width of 1/3 to the right of the just packed, starting at level R and ending with the current top border of the package (that is, it does not extend above the rectangles 1/2 <width <= 2/3). All remaining rectangles, which are narrower than 1/2 stripes, are packed with the same FFDH first of all into the formed region, and if they do not fit, then from the top. It sounds cumbersome in words, the picture should be clearer. And for those who are already tired of my literary exercises - a pseudo-code:
SF Algorithm

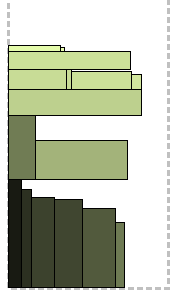
Apparently, this algorithm was imprisoned for a certain nature of the input data, well, any practical situation has a right to exist. Now you will understand everything yourself. Rectangles sorted, as usual, by non-increasing heights are combined in pairs so that the height difference in the pair does not exceed a given fraction, usually 0-10%. Another condition is that their total width fits in the strip. The resulting "super-rectangles" are packed together with the remaining without a pair using NFDH and FFDH, the best solution is selected.
There is a variation of this algorithm when the rectangles are sorted by width and combined vertically, with the same condition for the maximum deviation of the width in the pair by a given number of percent.
Join Algorithm
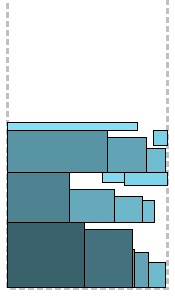
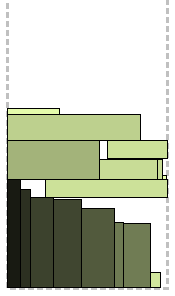
If you are still perplexed about remaining at the space levels, then this algorithm is for you. Rectangles are sorted by non-increasing heights (unexpectedly, yes?) And the BFDH algorithm with some modifications is applied. Each level has a “floor” and a “ceiling”. As long as possible, rectangles are packed on the "floor" from left to right. When the place ends, an attempt is made to pack on the “ceiling” from right to left; if there is no space on the ceiling, then only a new level begins. In the best traditions of BFDH, at every step all levels are viewed - first “floor”, then “ceiling” - for the most suitable place. Packaging, as you can see, is not bad. The method successfully packs the smallest rectangles on the “ceilings”.
FCNR Algorithm
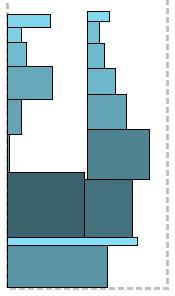
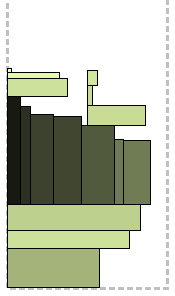
The time has come for “flat” algorithms, without dividing into levels. The Sleator algorithm uses the intuitive principle of packing a backpack: fold the largest items to the bottom and fill them up with small ones. Here is how it looks. From the rectangles, the widest, wider than half of the strip are selected, you guessed it, and randomly stacked on top of each other with alignment to the left. The remaining ones are sorted by non-increasing heights and begin to stack one after another from left to right from above to those already laid. As soon as their total width exceeds half the width of the strip, the remaining ones are scattered on each other either to the left (starting from the left edge of the strip), then to the right (from the middle), according to the principle "where at the moment there is less." As can be seen from the figures, it is more convenient to stack books with this method than boxes.
Sleator Algorithm

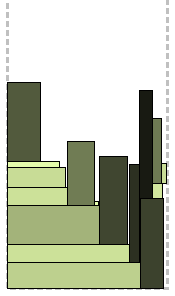
Again a levelless algorithm for which an additional “height map” is introduced:
This is an array by which, as the strip fills, you can track the least filled areas and their width. At the beginning it is filled with zeros. Rectangles are sorted by non-increasing, suddenly, widths. Then, at each step of the algorithm:
1. The position of the lowest region is calculated - the index of the minimum value of the array;
2. The most suitable rectangle is selected - firstly, it fits in this area, and secondly, it fills it as wide as possible;
3. If a suitable rectangle is found, it is placed in this area in one of the ways:
3.1. On the left edge of the area;
3.2 Closer to a higher neighbor, if one of the neighbors is the edge of the strip, then closer to the edge;
3.3 Closer to a less high neighbor, if one of the neighbors is the edge of the strip, then further from the edge. To the values of the array corresponding to the width of the rectangle, its height is added.
4. If there is no suitable rectangle, the area is “filled” by leveling its height to the height of the nearest edge.
Have you already wanted to write a bot playing Tetris using this algorithm?
Burke Algorithm
The result of each algorithm is the level of bandwidth, the less the better. It can be estimated by the ratio of the optimal to it:
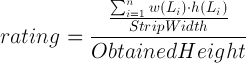
Compare the results obtained for the two given sets of source data:
We see that the Floor Ceiling algorithm won for both datasets. It can be noted that Sleator showed a much better result for the first set, and Join, on the contrary, is more suitable for the second. But all this is nothing more than statistics.
Due to its simple formulation, the task of binary packaging can be pulled to a huge number of practical applications: directly to packing objects or cutting material, distributing funds, planning tasks on clusters, etc. There are few refined problems in life, but, having limited some conditions, you can reduce the situation to a beautiful mathematical model that has a good solution, attainable in polynomial time. And once, as a result of the butterfly effect, the discarded conditions will take a lot of weight and the decision will fly to all Nameless. It is because of such assumptions that the world is imperfect.
Something I was distracted. In the next part I hope to talk about the online version of the task and offshore algorithms. Good luck!
Sources of inspiration:
Nthabiseng Ntene An Algorithmic Approach to the 2D Oriented Strip Packing Problem
David Pisinger Knapsack problem
Survey on two-dimensional packing
Level Algorithms and Shelf Algorithms (carefully, tear-eye design)
Code (Qt):
Algorithms packager.h packager. cpp
Gui window.h window.cpp renderarea.h renderarea.cpp main.cpp
UPD: Online algorithms
From ancient times (at least from the beginning of the last century), mathematicians wondered how to optimally place a certain amount of
The task of packing in containers ( Bin Packing Problem), one of the varieties of which is the problem of two-dimensional packaging (2-Dimensional Bin Packing). Having discarded several variations again, we finally come to two-dimensional packing in a semi-limited strip (2-Dimensional Strip Packing, 2DSP). Feel how much interesting is already behind the scenes? But we have not finished wading through the classification. 2DSP has two input options: when the set of packed objects is known in advance (offline problem) and when the data arrives in batches (online problem).
This article discusses algorithms for solving offline-variant 2DSP. Under the cut, there is a bit of materiel and a lot of pictures with colored squares.
What, in fact, is the problem?
As a special case of the two-dimensional packing problem, 2DSP consists in packing objects of a particular shape into a finite number of containers of a particular shape in such a way that the number of containers used is the smallest or the number or volume of objects (which pack) are the largest. The difference with two-dimensional packaging is that there is only one container, and instead of minimizing the number of containers, we minimize the height of one. We provide maximum packing density if you want.
Since the problem is NP-hard, research focuses mainly on developing approximate solution algorithms. (The genetic algorithm was mentioned on Habré) Approximate algorithms find the optimal solution with a certain accuracy, but do not guarantee optimal packaging for any data set. In this case, the criterion of optimality depends on what you tried to optimize.
I’ll talk about the simplest strategies and what it all applies to in life (except for a backpack with beer).
So, we have a set of n rectangles and a semi-limited container-glass with a fixed width W and infinite height. Each rectangle does not exceed W in width. The task is to put the rectangles in the glass without overlapping and intersecting so that the glass becomes as small as possible. Let's agree that all rectangles should be packed orthogonally, they cannot be rotated.
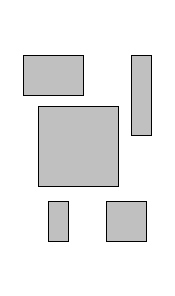 |  | 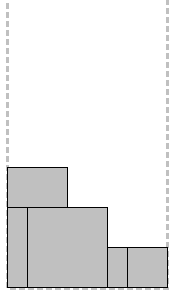 |  |
| Initial data (beginning of XX century, cubism) | Semi-limited lane | Packaging option (worse) | Packaging Option (Better) |
It can be seen that the problem has an ideal solution in which the height of the packed rectangles is equal to their total area divided by the width of the strip.
Zoo Algorithms
For the offline version of 2DSP, the size of all the packed rectangles is immediately known, so they can be sorted, selected according to a specific criterion, grouped or simply bumped into suitable places. Most algorithms are based on this:
- level (level)
- shelf (shelf)
- flat (plane)
Flat algorithms place rectangles strictly close to each other, but this is not the most successful strategy, as it might seem at first glance. Level ones divide the strip into levels equal in height to one of the selected rectangles, and put all the others on a specific level according to a certain criterion. Shelf shelves predetermine several shelves (shelves) at once, and push rectangles along them, this behavior is typical for online-algorithms, and this is a completely different story.
Than to extend to common words, it is better about everything in order.
Next Fit Decreasing High


The algorithm, as they say, "in the forehead." Rectangles are sorted by non-increasing height (Decreasing High hints), the highest is located in the lower left corner of the strip, thereby initializing the first level equal in height to it. The remaining rectangles are located from left to right, while there is space at the current level. A rectangle that does not fit on a level is placed on top to form the next level, and so on.
Illustrations for each algorithm will be made for the following two examples: for clarity, in the left, the shape of the rectangles tends to be elongated, in the right - more square.
NFDH Algorithm
Input: The number of rectangles to be packed n,
the dimensions of the rectangles
{w (Li); h (Li)} and the strip width W.
Output: The height of a packing obtained in the strip.
1: level = 0; h (level) = 0; w (level) = 0; i = 1
2: Sort the rectangles in order of non-increasing height such that h (L1) ≥ h (L2) ≥ ... ≥ h (Ln)
3: Pack rectangle Li left-justifed at the bottom of the strip
4: h (level) = h (Li); w (level) = w (Li)
5: for i = 2..n do
6: if W - w (level) ≥ w (Li) then
7: pack rectangle Li to the right of rectangle Li-1
8: w (level) + = w (Li)
9: else [W - w (level) <w (Li)]
10: create a new level above the previous one and pack rectangle Li on the new level
11: level ++; w (level) = w (Li); h (level) = h (level-1) + h (Li)
12: end if
13: end for
14: print H = h (level)First fit decreasing high


Similar to the previous algorithm, with the difference that for each next rectangle a place is sought not only at the last level, but starting from the lowest. Hence the “first fit” - the rectangle is placed on the first suitable level from below. Intuitively, the packaging will be better. Another significant difference is in performance, since in the worst case, you will have to consider all levels from the bottom up at every step.
FFDH Algorithm
Input: The number of rectangles to be packed n,
the dimensions of the rectangles
{w (Li); h (Li)} and the strip width W.
Output: The height of a packing obtained in the strip.
1: level = 0; h (level) = 0; i = 1; LevelNum = 1
2: Sort the rectangles in order of non-increasing height such that h (L1) ≥ h (L2) ≥ ... ≥ h (Ln)
3: Pack rectangle Li left-justifed at the bottom of the strip; h (level + 1) = h (Li)
4: for i = 2..n do
5: search all levels (from the bottom) for the lowest with sufficient space
6: if such a level exist then
7: pack rectangle Li left justified on that level
8: else [there is insufficient space in all existing levels]
9: LevelNum ++; level = LevelNum; h (level) = h (level-1) + h (Li)
10: pack rectangle Li on the new level
11: end if
12: end for
13: print H = h (level)Best fit decreasing high


Modification of the previous algorithm. Its essence is that of the levels suitable for packing the next rectangle, not the first, but the best one is chosen. The best level is one where there will be a minimum of space after packing the current rectangle. Simply put, the minimum suitable space is chosen, which contributes to a better filling of the levels.
BFDH Algorithm
Input: The number of rectangles to be packed n,
the dimensions of the rectangles
{w (Li); h (Li)} and the strip width W.
Output: The height of a packing obtained in the strip.
1: level = 0; h (level) = 0; i = 1; LevelNum = 1
2: Sort the rectangles in order of non-increasing height such that h (L1) ≥ h (L2) ≥ ... ≥ h (Ln)
3: Pack rectangle Li left-justifed at the bottom of the strip; h (level + 1) = h (Li)
4: for i = 2..n do
5: search all levels for the level with sufficient space and has minimum residual space
6: if such a level exist then
7: pack rectangle Li left justified on that level
8: else [there is insufficient space in all existing levels]
9: create a new level above the top-most level and pack rectangle Li
10: LevelNum ++; level = LevelNum; h (level) = h (level-1) + h (Li)
11: end if
12: end for
13: print H = h (level)Knapsack 0-1


It is worth staying in more detail. Knapsack 0-1 is a special case of the knapsack problem; It is noteworthy that in addition to answering the main question (no, not 42, but the resulting packaging volume) it also gives a solution - a list of items that need to be packaged. The procedure is as follows: rectangles are sorted by non-increasing height; the first rectangle is packed to a new level; for this level there is a solution to the Knapsack 0-1 problem, which gives us a list of rectangles maximized in area. The selected rectangles are packed and retrieved from the unpacked list, the level closes and a new one opens - initialized, as usual, the first (highest) of the remaining ones. Repeat until there are rectangles.
Algorithm KP01
Input: The number of rectangles to be packed n,
the dimensions of the rectangles
{w (Li); h (Li)} and the strip width W.
Output: The height of a packing obtained in the strip.
1: Sort the rectangles in order of non-increasing height such that h (L1) ≥ h (L2) ≥ ... ≥ h (Ln)
2: level = 0
3: while there are unpacked rectangles do
4: pack first unpacked rectangle, Li say
5: h (level) + = h (Li)
6: solve KP01 instance
7: pack selected rectangles
8: level = level + 1
9: end while
10: print H = h (level)Split fit


Algorithm designed to improve FFDN on the principle of "divide and conquer." First, rectangles that are wider than half the strip are selected. They will be packed first. Of these, even wider ones are chosen — wider than 2/3 of the strip; they are packed with the FFDH algorithm. Above them, starting at the next level(let's call it level R), the remaining ones are packed, those that are still wider than 1/2, but already 2/3. They are also packaged using FFDH. This separation creates a free region with a width of 1/3 to the right of the just packed, starting at level R and ending with the current top border of the package (that is, it does not extend above the rectangles 1/2 <width <= 2/3). All remaining rectangles, which are narrower than 1/2 stripes, are packed with the same FFDH first of all into the formed region, and if they do not fit, then from the top. It sounds cumbersome in words, the picture should be clearer. And for those who are already tired of my literary exercises - a pseudo-code:
SF Algorithm
Input: The number of rectangles to be packed n,
the dimensions of the rectangles
{w (Li); h (Li)} and the strip width W.
Output: The height of a packing obtained in the strip.
1: Let m ≥ 1 be the largest integer for which all rectangles in L
have width at most 1 = m
2: Partition the list of rectangles L into two sublists L1 and L2
such that L1 is a list of rectangles of width greater than
1 / (m + 1), while L2 is a list of rectangles of width at most 1 / (m + 1)
3: Pack the L1 rectangles into the strip, using the FFDH algorithm
4: Rearrange the blocks of this packing such that those of width
greater than (m + 1) / (m + 2) are below those of width
at most (m + 1) / (m + 2)
5: Pack rectangles of width at most 1 / (m + 2) into the region R
using FFDH algorithm such that no rectangle overlaps the top
of R and those failing to fit in R are packed above the packing of L1
6: Output the height of the strip, found by adding the height of each levelJoin


Apparently, this algorithm was imprisoned for a certain nature of the input data, well, any practical situation has a right to exist. Now you will understand everything yourself. Rectangles sorted, as usual, by non-increasing heights are combined in pairs so that the height difference in the pair does not exceed a given fraction, usually 0-10%. Another condition is that their total width fits in the strip. The resulting "super-rectangles" are packed together with the remaining without a pair using NFDH and FFDH, the best solution is selected.
There is a variation of this algorithm when the rectangles are sorted by width and combined vertically, with the same condition for the maximum deviation of the width in the pair by a given number of percent.
Join Algorithm
Input: The number of rectangles to be packed n,
the dimensions of the rectangles
{w (Li); h (Li)}, the constant gamma as a
percentage and the strip width W.
Output: The height of a packing obtained in the strip.
1: Sort the rectangles in order of non-increasing height such that h (L1) ≥ h (L2) ≥ ... ≥ h (Ln)
2: j = 1
3: while j + 1 ≤ n do
4: if (h (Lj) - h (Lj + 1)) / h (Lj) * 100 <gamma
and w (Lj) + w (Lj + 1) ≤ W then
5: w (Lj) + = w (Lj + 1)
6: j + = 2
7: else
8: j ++
9: end if
10: end while
11: Execute the NFDH and FFDH algorithms to pack the rectangles
12: From the best solution, construct a feasible packing of the original instance
13: Output the height of the strip, found by adding the height of each levelFloor Ceiling No Rotation


If you are still perplexed about remaining at the space levels, then this algorithm is for you. Rectangles are sorted by non-increasing heights (unexpectedly, yes?) And the BFDH algorithm with some modifications is applied. Each level has a “floor” and a “ceiling”. As long as possible, rectangles are packed on the "floor" from left to right. When the place ends, an attempt is made to pack on the “ceiling” from right to left; if there is no space on the ceiling, then only a new level begins. In the best traditions of BFDH, at every step all levels are viewed - first “floor”, then “ceiling” - for the most suitable place. Packaging, as you can see, is not bad. The method successfully packs the smallest rectangles on the “ceilings”.
FCNR Algorithm
Input: The number of rectangles to be packed n,
the dimensions of the rectangles
{w (Li); h (Li)} and the strip width W.
Output: The height of a packing obtained in the strip.
1: Sort the rectangles in order of non-increasing height such that h (L1) ≥ h (L2) ≥ ... ≥ h (Ln)
2: for i = 1..n do
3: if Li is ceiling feasible then
4: pack Li on ceiling with minimum residual space
5: else [Li is not ceiling feasible]
6: if Li is floor feasible then
7: pack Li on the floor with minimum residual space
8: else [Li is not floor feasible]
9: level ++;
10: end if
11: end if
12: end for
13: Output the height H of the strip, found by adding the height of each levelSleator


The time has come for “flat” algorithms, without dividing into levels. The Sleator algorithm uses the intuitive principle of packing a backpack: fold the largest items to the bottom and fill them up with small ones. Here is how it looks. From the rectangles, the widest, wider than half of the strip are selected, you guessed it, and randomly stacked on top of each other with alignment to the left. The remaining ones are sorted by non-increasing heights and begin to stack one after another from left to right from above to those already laid. As soon as their total width exceeds half the width of the strip, the remaining ones are scattered on each other either to the left (starting from the left edge of the strip), then to the right (from the middle), according to the principle "where at the moment there is less." As can be seen from the figures, it is more convenient to stack books with this method than boxes.
Sleator Algorithm
Input: The number of rectangles to be packed n,
the dimensions of the rectangles
{w (Li); h (Li)} and the strip width W.
Output: The height of a packing obtained in the strip.
1: Partition L into two sublists L1 and L2 consisting of rectangles
of width greater than 1/2 and at most 1/2 respectively.
2: Stack all the rectangles in L1 left justified on top of
one another starting at the bottom of the strip. Compute hstack
3: Packing will continue above Hstack
4: Sort the rectangles in L2 according to non-increasing height
such that h (Li) ≥ h (Li + 1) for i <n
5: Let Htall be the height of the tallest rectangle in list L2.
6: Pack the rectangles, left justified from the left to the right
edge of the strip until there is insufficient space to pack
a rectangle or all of the rectangles have been packed
7: Partition the strip with a vertical line into two equal segments.
There is possibly one rectangle whose interior may be intercepted
by the vertical line.
8: Let Hright and Hleft be the height of the rectangle on the right
(resp. left) half of the strip whose left (resp. right) edge
is adjacent to the vertical line or whose interior is intercepted
by the vertical line
9: while there are unpacked rectangles do
10: Draw horizontal lines of length half across
the rectangles whose height is Hleft and Hright
11: All subsequent packing will either be on the left
or right segment of the strip
12: Select the segment with minimum height and pack
rectangles from the edge of the strip to the
vertical line until all rectangles have been
packed or there is a rectangles which does not fit
13: end while
14: print H = max {Hleft; Hright}Burke


Again a levelless algorithm for which an additional “height map” is introduced:
| | | _ _ ___ | | | | | | _ | _ | | | | | | _ | | | | | | _ _ _ _ _ _ _ _ | | .. | _ | _ | _ | _ _ | _ | _ _ | 0 0 0 0 0 0 0 0 1 0 3 2 3 0 3 3
This is an array by which, as the strip fills, you can track the least filled areas and their width. At the beginning it is filled with zeros. Rectangles are sorted by non-increasing, suddenly, widths. Then, at each step of the algorithm:
1. The position of the lowest region is calculated - the index of the minimum value of the array;
2. The most suitable rectangle is selected - firstly, it fits in this area, and secondly, it fills it as wide as possible;
3. If a suitable rectangle is found, it is placed in this area in one of the ways:
3.1. On the left edge of the area;
3.2 Closer to a higher neighbor, if one of the neighbors is the edge of the strip, then closer to the edge;
3.3 Closer to a less high neighbor, if one of the neighbors is the edge of the strip, then further from the edge. To the values of the array corresponding to the width of the rectangle, its height is added.
4. If there is no suitable rectangle, the area is “filled” by leveling its height to the height of the nearest edge.
Have you already wanted to write a bot playing Tetris using this algorithm?
Burke Algorithm
Input: The number of rectangles to be packed n,
the dimensions of the rectangles
{w (Li); h (Li)} and the strip width W.
Output: The height of a packing obtained in the strip.
1: Sort the rectangles according to non-increasing width such that w (Li) ≥ w (Li + 1) ≥ .. ≥ W (Ln)
2: for each placement policy
(leftmost, tallest neighbor, smallest neighbor) do
3: while Rectangles not packed do
4: find lowest gap
5: if w (Li) ≤ GapWidth then
6: place best fitting rectangle using placement policy
7: raise elements of array to appropriate height
8: else
9: raise gap to height of the lowest neighbor
10: end if
11: end while
12: end for
13: The elements of the array with greatest entry give the total height of the packing
14: Compare total packing heights obtained by each placement policy and return the best solutionWho's better?
The result of each algorithm is the level of bandwidth, the less the better. It can be estimated by the ratio of the optimal to it:
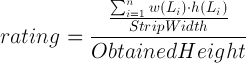
Compare the results obtained for the two given sets of source data:
| Optimal solution | Nfdh | Ffdh | Bfdh | Kp01 | SF | Join | FCNR | Sleator | Bruke | |
|---|---|---|---|---|---|---|---|---|---|---|
| Set 1 | 149 | 0.65 | 0.71 | 0.71 | 0.71 | 0.75 | 0.61 | 0.83 | 0.68 | 0.72 |
| Set 2 | 140 | 0.66 | 0.77 | 0.77 | 0.78 | 0.77 | 0.70 | 0.84 | 0.51 | 0.71 |
We see that the Floor Ceiling algorithm won for both datasets. It can be noted that Sleator showed a much better result for the first set, and Join, on the contrary, is more suitable for the second. But all this is nothing more than statistics.
Epilogue
Due to its simple formulation, the task of binary packaging can be pulled to a huge number of practical applications: directly to packing objects or cutting material, distributing funds, planning tasks on clusters, etc. There are few refined problems in life, but, having limited some conditions, you can reduce the situation to a beautiful mathematical model that has a good solution, attainable in polynomial time. And once, as a result of the butterfly effect, the discarded conditions will take a lot of weight and the decision will fly to all Nameless. It is because of such assumptions that the world is imperfect.
Something I was distracted. In the next part I hope to talk about the online version of the task and offshore algorithms. Good luck!
Sources of inspiration:
Nthabiseng Ntene An Algorithmic Approach to the 2D Oriented Strip Packing Problem
David Pisinger Knapsack problem
Survey on two-dimensional packing
Level Algorithms and Shelf Algorithms (carefully, tear-eye design)
Code (Qt):
Algorithms packager.h packager. cpp
Gui window.h window.cpp renderarea.h renderarea.cpp main.cpp
UPD: Online algorithms
