Classification of documents by the support vector method
It took me three years ago to make a text classifier. In this article I will talk about how it worked and generally some aspects of the implementation and testing of such algorithms.
Classification, according to Wikipedia, is one of the tasks of information retrieval, which consists in assigning a document to one of several categories based on the content of the document.
This is what we will do.
I think there is no need to describe why this is necessary, because the classification of documents has long been used in information retrieval, in the search for plagiarism, and so on.
To train the classifier (if our classifier is trainable) you need some collection of documents. However, as for the tests.
To do this, there are various test collections of texts, which basically can be easily found on the Internet. I used the RCV1 collection (Reuters Corpus Volume 1). This is a collection of Reuters hand-sorted news from August 1996 to August 1997. The collection contains about 810,000 news articles in English. It is constantly used for a variety of research in the field of information retrieval and text processing.
The collection contains hierarchical categories (one document can belong to different categories, for example, to the economy and oil at the same time). Each category has its own code, and these codes are already attributed to the news (about eighty categories in total). For example, four categories are at the head of the hierarchy: CCAT (Corporate / Industrial), ECAT (Economics), GCAT (Government / Social), and MCAT (Markets).
A complete list of categories can be found here.
Now we will deal with a few more important points. Firstly, to train the classifier, it would be nice to also stamp the texts and throw out the stop words.
Such processing is an already established way to reduce the dimension of a task and improve productivity.
Now we abstract from text documents and consider one of the existing classification algorithms.
I will not load details and mathematical calculations here. If they are interesting, then they can be found, for example, on Wikipedia or on Habr .
I will tell you briefly.
Suppose we have many points in an n-dimensional space, and each of the points belongs to only one of the two classes. If we can somehow divide them into two sets by a hyperplane of dimension n-1, then this will immediately solve the problem. This does not always happen, but if the set is linearly separable, then we are lucky:
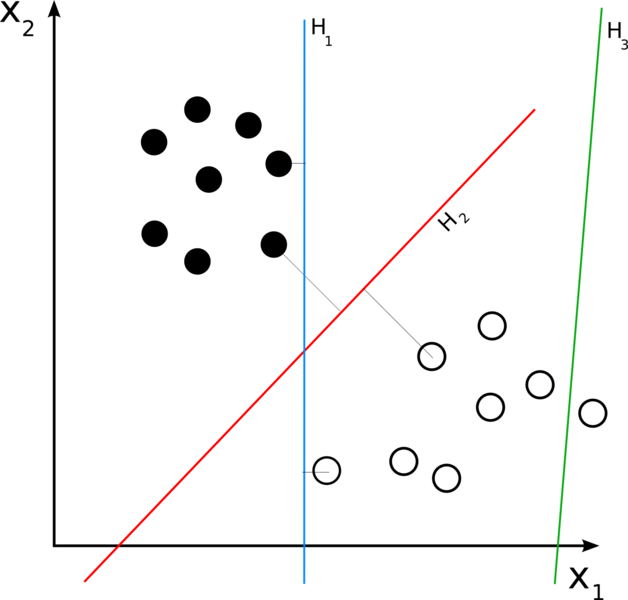
The classifier works the better, the greater the distance from the dividing hyperplane to the nearest point of the set. We need to find just such a hyperplane from all possible. It is called the optimal dividing hyperplane:

A simple idea is used for the search: to construct two parallel hyperplanes between which there are no points of the set and to maximize the distance between them. The points closest to parallel hyperplanes are called support vectors, which gave the name to the method.
But what if the set is not linearly separable? Moreover, most likely this is so. In this case, we simply allow the classifier to divide the sets so that points can appear between the hyperplanes (hence the error of the classifier, which we are trying to minimize). Having found such a hyperplane, classification becomes a matter of technology: you need to look at which side of the hyperplane the vector turned out to be, the class of which must be determined.
Of course, you can implement the algorithm yourself. But if there are good ready-made solutions, this can lead to a waste of a lot of time, and not the fact that your implementation will be better or at least the same.
There is a great implementation of support vector machine called SVM light . It was created at the Technical University of Dortmund and is distributed free of charge (for research purposes only). There are several implementation options (for example, one that can learn from relational databases), but you can take the simplest one that works with text files. Such a classifier consists of two executable files - training and classifying modules.
The training module receives a text file with training data as an input. The file must contain vectors labeled +1 or -1, depending on which of the two classes it belongs to.
It looks like this:
-1 0 0 0 0 0 0 6 0 0 0 6.56 0 0 0 0 0 0 0 45.56 0 0 0 0 0 0.5 0 0 0 0 0 0 0
Also, the module will understand the following entry:
-1 7: 6 11: 6.56 19: 45.56 25: 0.5 (that is, you can list only nonzero values with an index).
The second module receives a text file with data to be classified as input. The format is the same as for training. After classification, a res.txt is created in which the results are recorded.
Now let’s see how svm can be applied to document classification. Where to get the vectors from? How to determine which categories our document belongs to, if there are 80 in total, and svm can only determine whether it belongs to one of two classes?
Presenting a document as a vector is not difficult. First you need to make a collection dictionary - this is a list of all the words that appear in this collection (for the RCV1 collection, it's 47,000 words). The number of words will be the dimension of the vectors. After that, the document is presented in the form of a vector, where the i-th element is a measure of the occurrence of the i-th word of the dictionary in the document. It can be + 1 or -1 depending on whether the word is included in the document or not, or the number of occurrences. Or the "share" of the word in the document. There are many options. As a result, vectors of large dimension are obtained, where most of the elements are zeros.
If we have 80 categories, we need to run the classifier 80 times. More precisely, we should have 80 classifiers for each category, able to determine whether the document falls into this category or not.
To test the classifier, you can use part of the same collection (only then you should not use this part in training) by comparing the results of the classifier with manual results.
To evaluate the work of classifiers, several metrics are used:
Here kw is the number of documents that the classifier incorrectly marked as not belonging to the desired category.
kr - the number of documents that the classifiers correctly noted as related to the desired category.
r - the total number of documents related to the desired category according to the classifier.
n is the total number of documents related to the desired category.
Of these metrics, Precision and Recall are the most important, as they show how much we were mistaken in assigning a category to a document and how generally our classifier randomly works. The closer both metrics are to one, the better.
And a small example. Having compiled the vector, taking as a measure of the word in the document its “share” (the number of occurrences of the word in the document divided by the total number of words in the document), and having trained the classifier for 32000 documents and when classifying 3000, the following results were obtained:
Precision = 0.95
Recall = 0.75
Not bad results, with them the classifier can be used to process new data.
About RCV1:
About RCV1
Here you can find the collection
About SVM:
Wikipedia
A large article
Classification
Classification, according to Wikipedia, is one of the tasks of information retrieval, which consists in assigning a document to one of several categories based on the content of the document.
This is what we will do.
I think there is no need to describe why this is necessary, because the classification of documents has long been used in information retrieval, in the search for plagiarism, and so on.
Collection
To train the classifier (if our classifier is trainable) you need some collection of documents. However, as for the tests.
To do this, there are various test collections of texts, which basically can be easily found on the Internet. I used the RCV1 collection (Reuters Corpus Volume 1). This is a collection of Reuters hand-sorted news from August 1996 to August 1997. The collection contains about 810,000 news articles in English. It is constantly used for a variety of research in the field of information retrieval and text processing.
The collection contains hierarchical categories (one document can belong to different categories, for example, to the economy and oil at the same time). Each category has its own code, and these codes are already attributed to the news (about eighty categories in total). For example, four categories are at the head of the hierarchy: CCAT (Corporate / Industrial), ECAT (Economics), GCAT (Government / Social), and MCAT (Markets).
A complete list of categories can be found here.
Now we will deal with a few more important points. Firstly, to train the classifier, it would be nice to also stamp the texts and throw out the stop words.
- Stemming. When classifying us, it doesn’t matter how the word “oil” is written (“oil”, “oil”, “oil”, “oil”) - we will still understand that this is about oil. Bringing words to the same mind is called stemming. There are ready-made solutions for stamping texts in English, for example , this implementation of the Porter algorithm . This library is written in java at Indiana University and is freely distributed. I didn’t look in Russian, maybe there is something too.
- Stop words. Everything is clear here. The words “and”, “but”, “by”, “from”, “under” and so on, do not affect the classification in any way, since they are found everywhere. In practice, they usually take some of the most popular words in the collection and throw them away (numbers can also be thrown away). You can just take the list from here.
Such processing is an already established way to reduce the dimension of a task and improve productivity.
Support Vector Method
Now we abstract from text documents and consider one of the existing classification algorithms.
I will not load details and mathematical calculations here. If they are interesting, then they can be found, for example, on Wikipedia or on Habr .
I will tell you briefly.
Suppose we have many points in an n-dimensional space, and each of the points belongs to only one of the two classes. If we can somehow divide them into two sets by a hyperplane of dimension n-1, then this will immediately solve the problem. This does not always happen, but if the set is linearly separable, then we are lucky:

The classifier works the better, the greater the distance from the dividing hyperplane to the nearest point of the set. We need to find just such a hyperplane from all possible. It is called the optimal dividing hyperplane:

A simple idea is used for the search: to construct two parallel hyperplanes between which there are no points of the set and to maximize the distance between them. The points closest to parallel hyperplanes are called support vectors, which gave the name to the method.
But what if the set is not linearly separable? Moreover, most likely this is so. In this case, we simply allow the classifier to divide the sets so that points can appear between the hyperplanes (hence the error of the classifier, which we are trying to minimize). Having found such a hyperplane, classification becomes a matter of technology: you need to look at which side of the hyperplane the vector turned out to be, the class of which must be determined.
Ready implementation
Of course, you can implement the algorithm yourself. But if there are good ready-made solutions, this can lead to a waste of a lot of time, and not the fact that your implementation will be better or at least the same.
There is a great implementation of support vector machine called SVM light . It was created at the Technical University of Dortmund and is distributed free of charge (for research purposes only). There are several implementation options (for example, one that can learn from relational databases), but you can take the simplest one that works with text files. Such a classifier consists of two executable files - training and classifying modules.
Training
The training module receives a text file with training data as an input. The file must contain vectors labeled +1 or -1, depending on which of the two classes it belongs to.
It looks like this:
-1 0 0 0 0 0 0 6 0 0 0 6.56 0 0 0 0 0 0 0 45.56 0 0 0 0 0 0.5 0 0 0 0 0 0 0
Also, the module will understand the following entry:
-1 7: 6 11: 6.56 19: 45.56 25: 0.5 (that is, you can list only nonzero values with an index).
Classification
The second module receives a text file with data to be classified as input. The format is the same as for training. After classification, a res.txt is created in which the results are recorded.
svm for document classification
Now let’s see how svm can be applied to document classification. Where to get the vectors from? How to determine which categories our document belongs to, if there are 80 in total, and svm can only determine whether it belongs to one of two classes?
The document is a vector
Presenting a document as a vector is not difficult. First you need to make a collection dictionary - this is a list of all the words that appear in this collection (for the RCV1 collection, it's 47,000 words). The number of words will be the dimension of the vectors. After that, the document is presented in the form of a vector, where the i-th element is a measure of the occurrence of the i-th word of the dictionary in the document. It can be + 1 or -1 depending on whether the word is included in the document or not, or the number of occurrences. Or the "share" of the word in the document. There are many options. As a result, vectors of large dimension are obtained, where most of the elements are zeros.
80 categories - 80 classifiers
If we have 80 categories, we need to run the classifier 80 times. More precisely, we should have 80 classifiers for each category, able to determine whether the document falls into this category or not.
Tests. Metrics
To test the classifier, you can use part of the same collection (only then you should not use this part in training) by comparing the results of the classifier with manual results.
To evaluate the work of classifiers, several metrics are used:
- Accuracy = ((r - kr) + kw) / n
In fact, this is accuracy. - Precision = kr / n
- Recall = kr / r
Here kw is the number of documents that the classifier incorrectly marked as not belonging to the desired category.
kr - the number of documents that the classifiers correctly noted as related to the desired category.
r - the total number of documents related to the desired category according to the classifier.
n is the total number of documents related to the desired category.
Of these metrics, Precision and Recall are the most important, as they show how much we were mistaken in assigning a category to a document and how generally our classifier randomly works. The closer both metrics are to one, the better.
And a small example. Having compiled the vector, taking as a measure of the word in the document its “share” (the number of occurrences of the word in the document divided by the total number of words in the document), and having trained the classifier for 32000 documents and when classifying 3000, the following results were obtained:
Precision = 0.95
Recall = 0.75
Not bad results, with them the classifier can be used to process new data.
References
About RCV1:
About RCV1
Here you can find the collection
About SVM:
Wikipedia
A large article
