Mathematical Fundamentals Auto Layout
Many developers believe that Auto Layout is a brake and problem thing, and it is extremely difficult to debug it. And it’s good if this conclusion is made on the basis of my own experience, and sometimes it happens simply “I heard, I won’t even try to make friends with it.”
But perhaps the reason is not outside, but inside. For example, the world's most dangerous birds will not attack people for no reason, just for the sake of self-defense. Therefore, try for a second to assume that this is not Auto Layout is bad, and you do not understand it well enough and do not know how to cook. So did Anton Sergeyev and dive into the theory in order to understand everything precisely. We are offered a finished squeeze about the mathematical foundations of Auto Layout.

Auto Layout is a layout system . Before delving into it, let's talk about modern layout in general. Then we will deal with Auto Layout - let's figure out what problem it solves and how it does it. Consider the features in the implementation of Auto Layout in iOS , and try to develop practical tips that can help you work with it.
This story will be very close to a mathematical article, so we first agree on the notation in order to speak the same language.
About the speaker: Anton Sergeev ( antonsergeev88 ) works in the Yandex.Maps team, deals with a mobile client for Maps on iOS. Prior to mobile development, he was in charge of power plant control systems, where the price of errors in the code is too high to be tolerated.
Legend
Systems of linear equations are familiar to us from school — indicated by a curly bracket, and their solution is already without. Also, systems of linear equations have entities with which Auto Layout operates - restrictions. Denoted by a straight line.
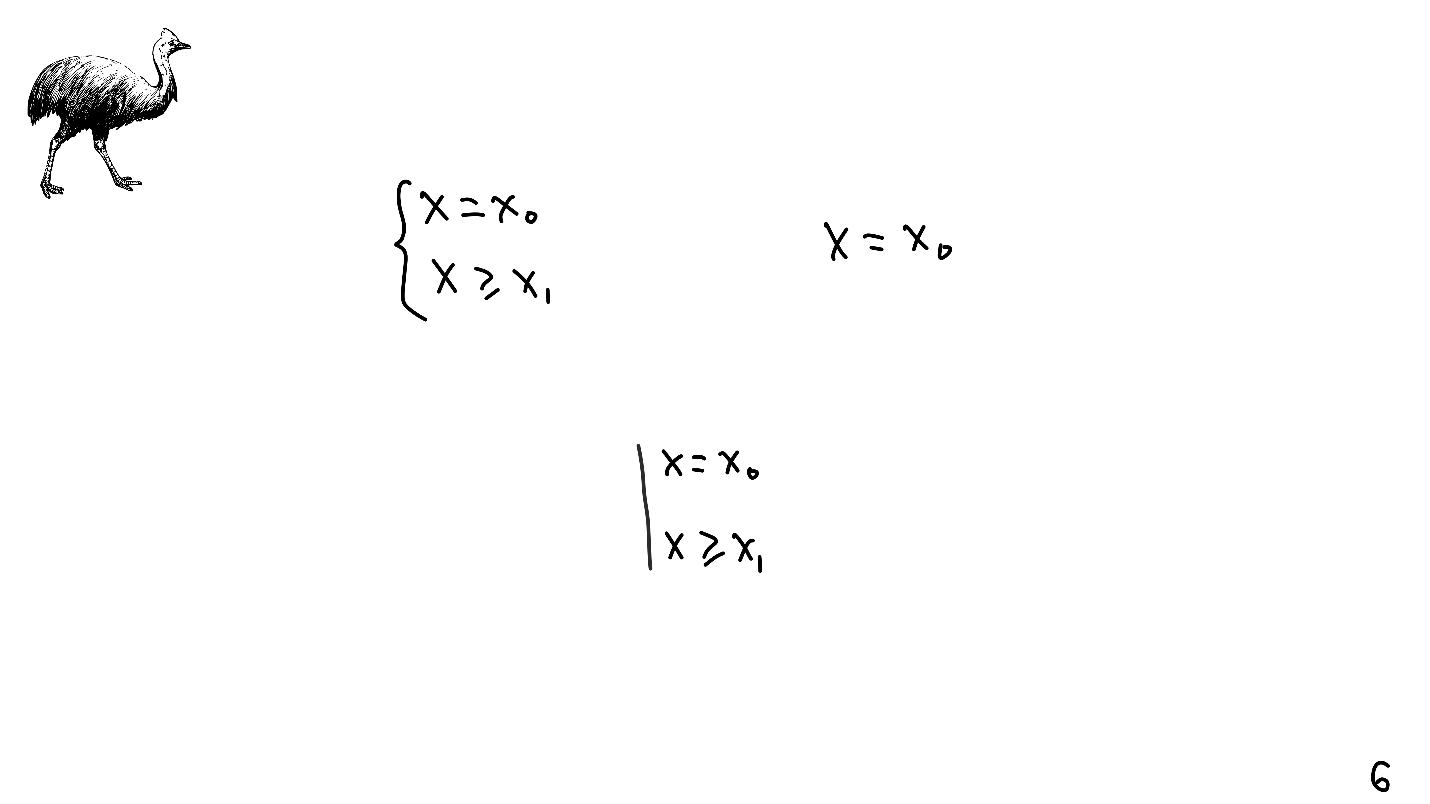
A strange and, as we already know, dangerous bird is not accidentally drawn in the upper corner of the slide. In honor of the cassowary (lat. Cassowary), which, of course, lives in Australia, an algorithm is named in all our iPhones.
In Auto Layout there are limitations, we will designate them with colors in order of priority: red - required; yellow - high; blue - low.
Layout
When I made the presentation, I had various elements on the screen, for example, cassowary. To do this, I determined that the cazuar is a rectangular picture. You need to place it on a sheet that has axes and its coordinate system, and for this I determined the coordinates of the upper left corner, width and height.
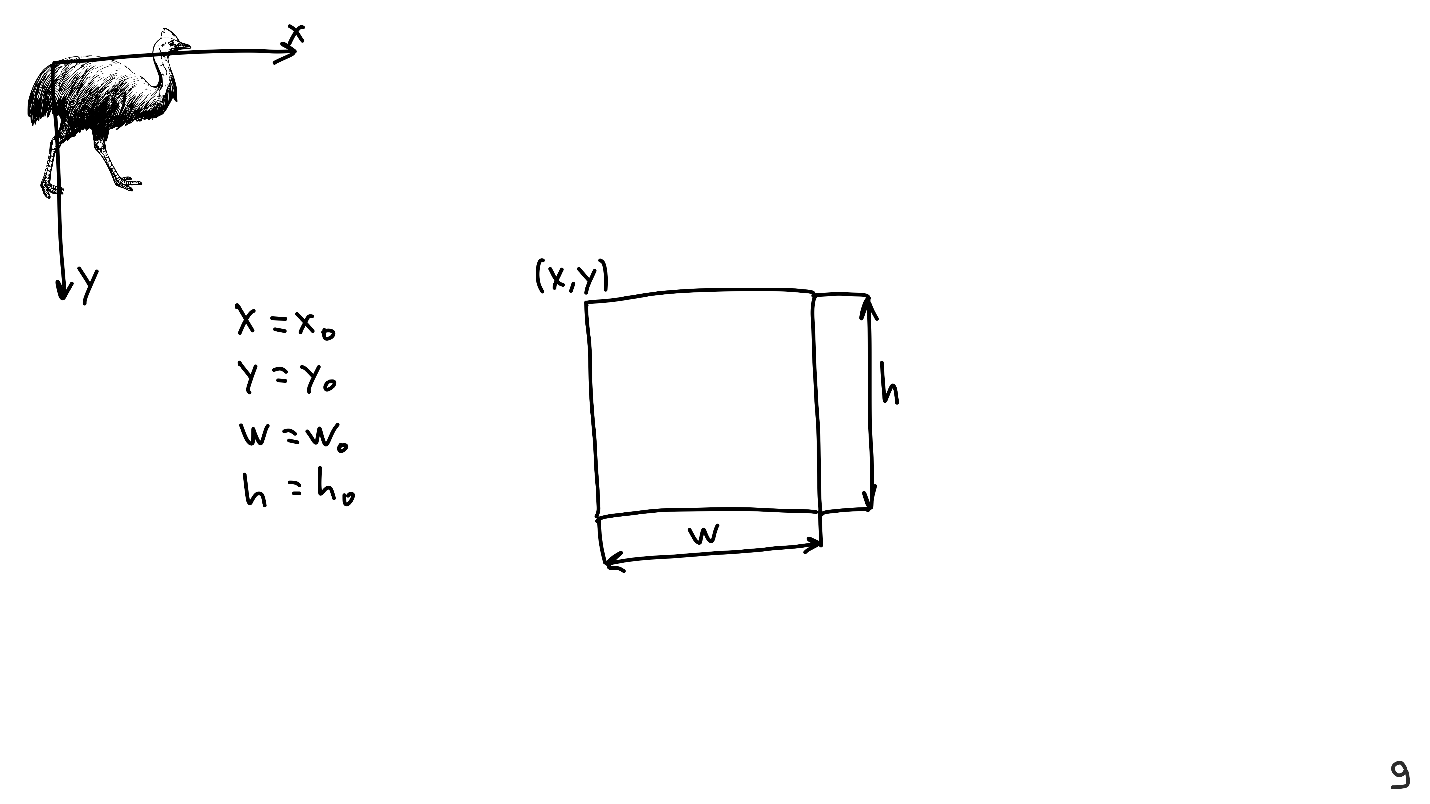
Knowing these four values is enough to present any View.
Algorithm number 1
While we had cassowary on a sheet, we unobtrusively described the first layout algorithm:
The algorithm works, but is rather complicated to use, so we will further simplify it.
Suppose that below - the solution of some system of linear equations.
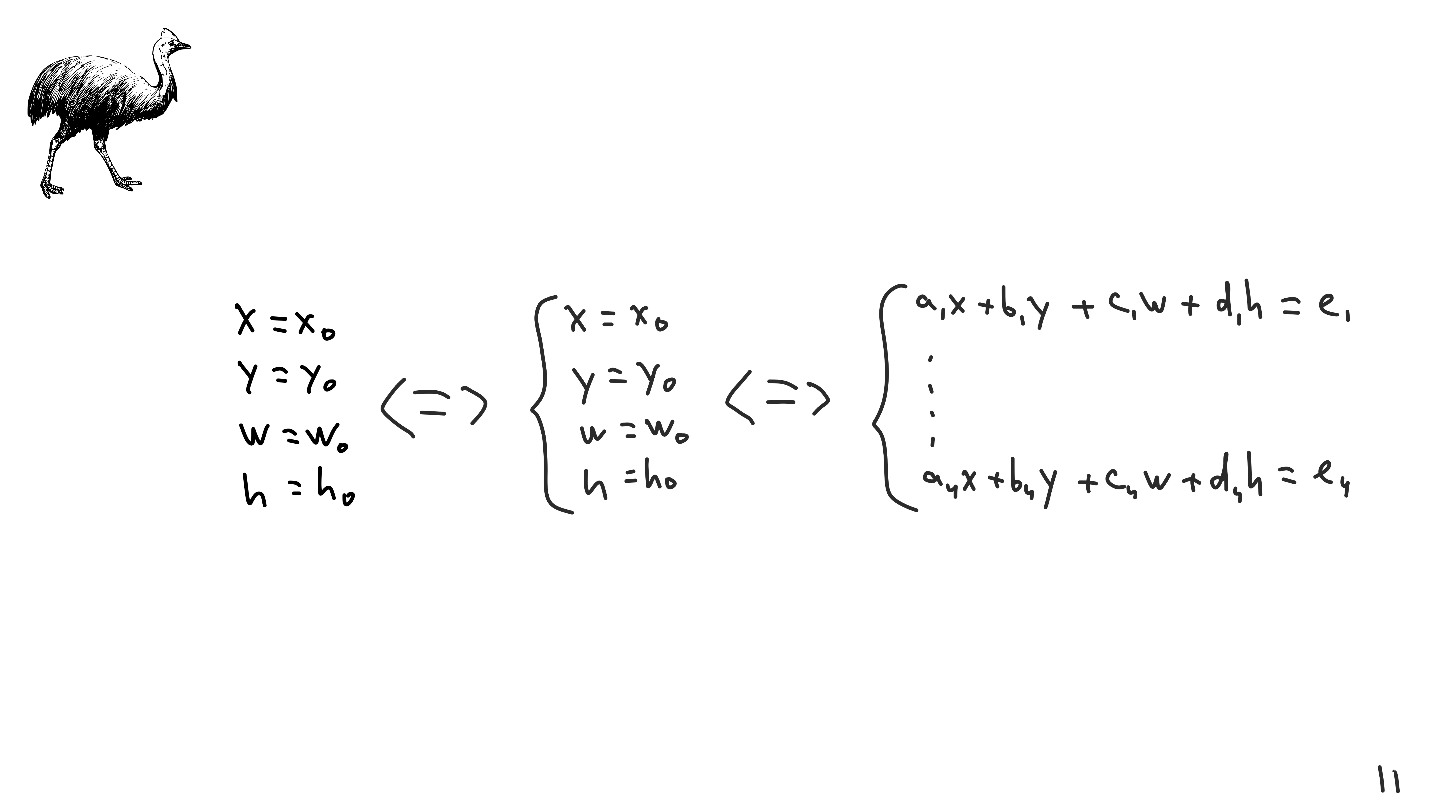
The system of linear equations is special in that a mass of operations is defined above it: folding the lines, multiplying them by constants, etc. These operations are called linear transformations, and with their help the system is reduced to an arbitrary form.
The beauty of linear transformations is that they are reversible. This brings us to an interesting and rather subtle idea, from which the whole modern layout begins.
Let there is a View - a rectangle with its own coordinates and size. We want to arrange it so that the center coincides with the given point. We will model the center using linear transformations -coordinate of the upper left corner + half width .
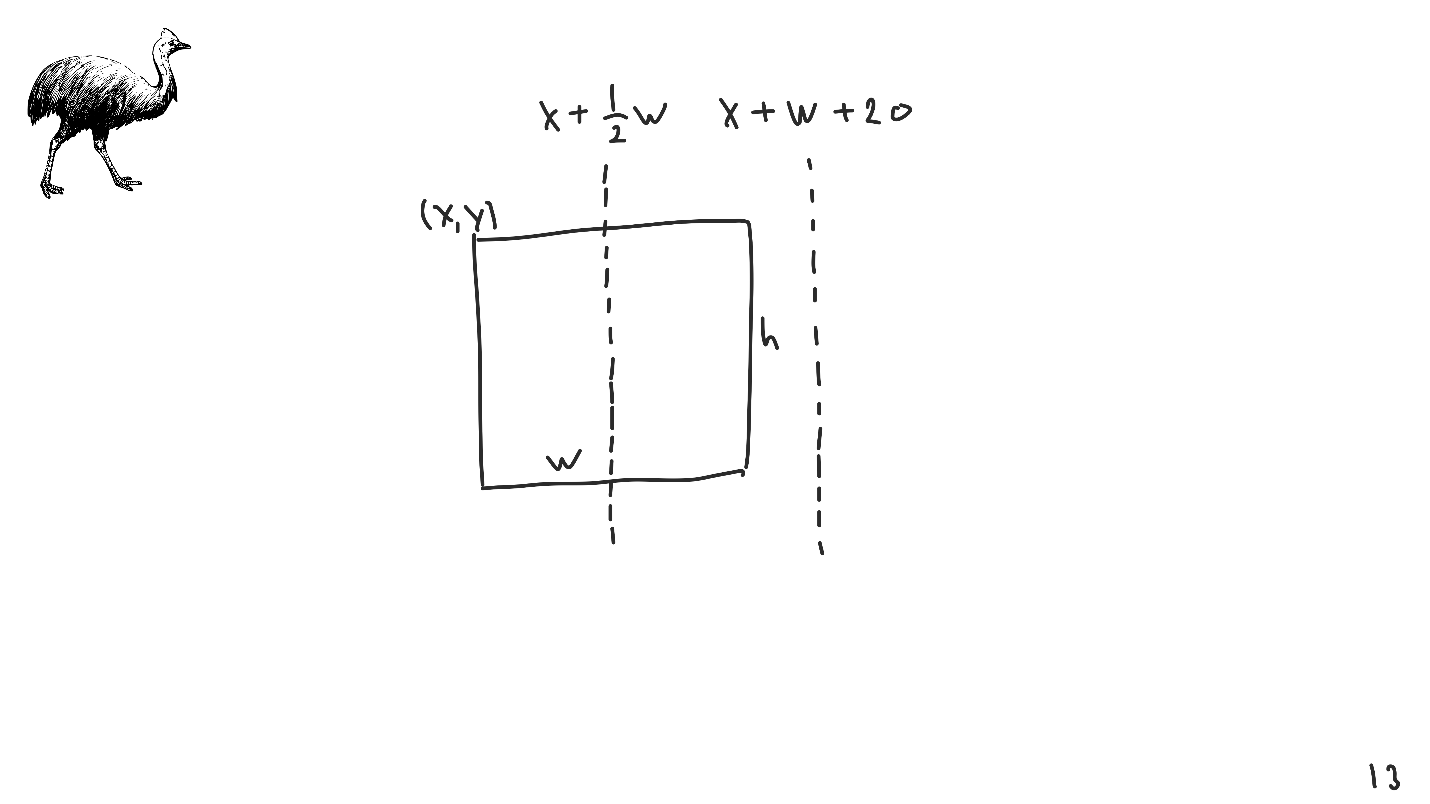
We modeled the center by a linear transformation, it was not there: there were only the coordinates of the left upper point, the width and height.
Similarly, you can simulate any other indents, for example, 20 points from the right corner.
Consider an elementary example. We write out a system with which we establish the coordinates of the middle and right side, the width and the ratio between width and height. We solve the system and get an answer.
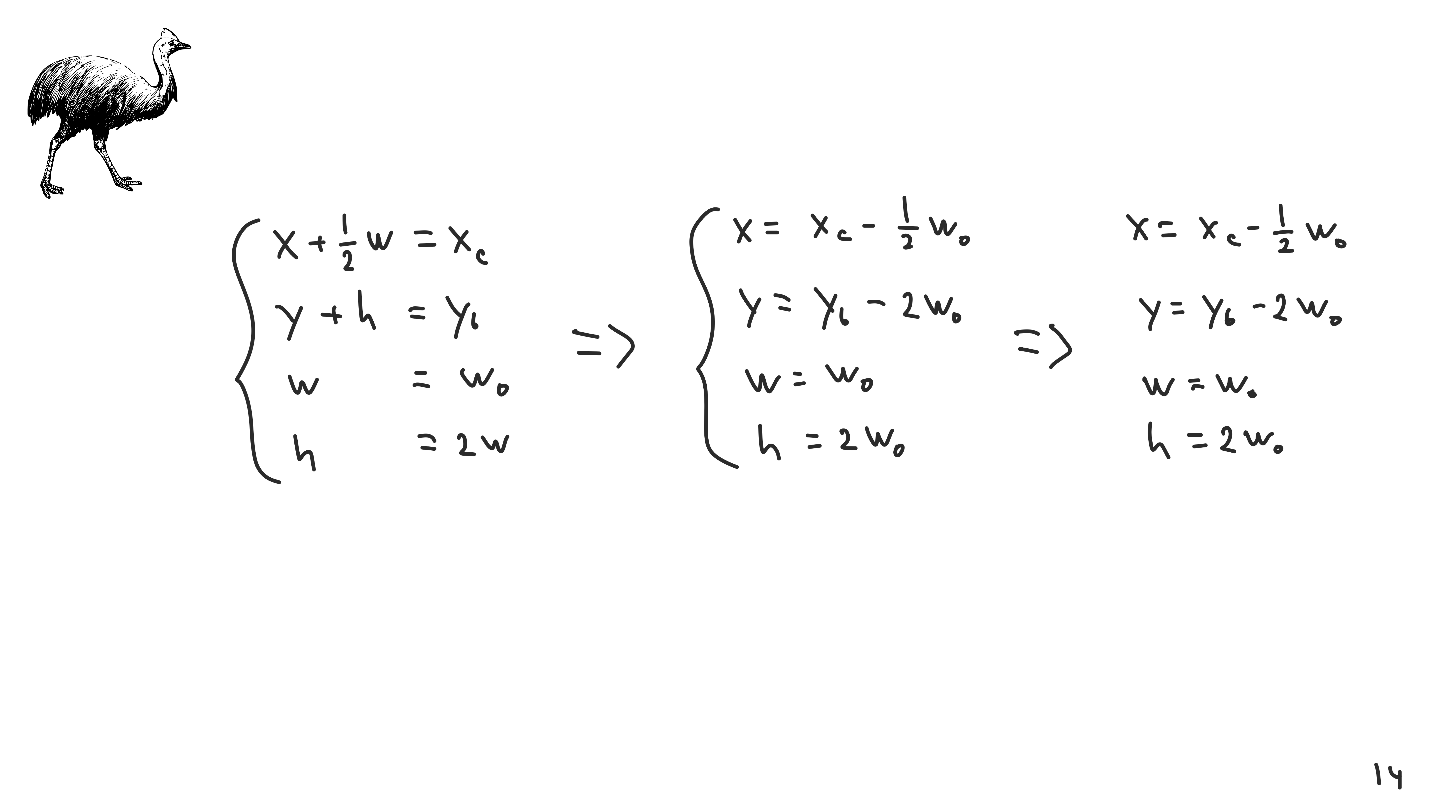
So we come to the second algorithm.
Algorithm number 2
The second iteration of the algorithm consists of the following items:
Imagine that we were in the twentieth century, at a time when computer technology was just emerging, and were the first to reach the creation of our typesetting system. Invented, packed, given to the user, and he begins to use it - fills in the initial parameters and transmits to our system.
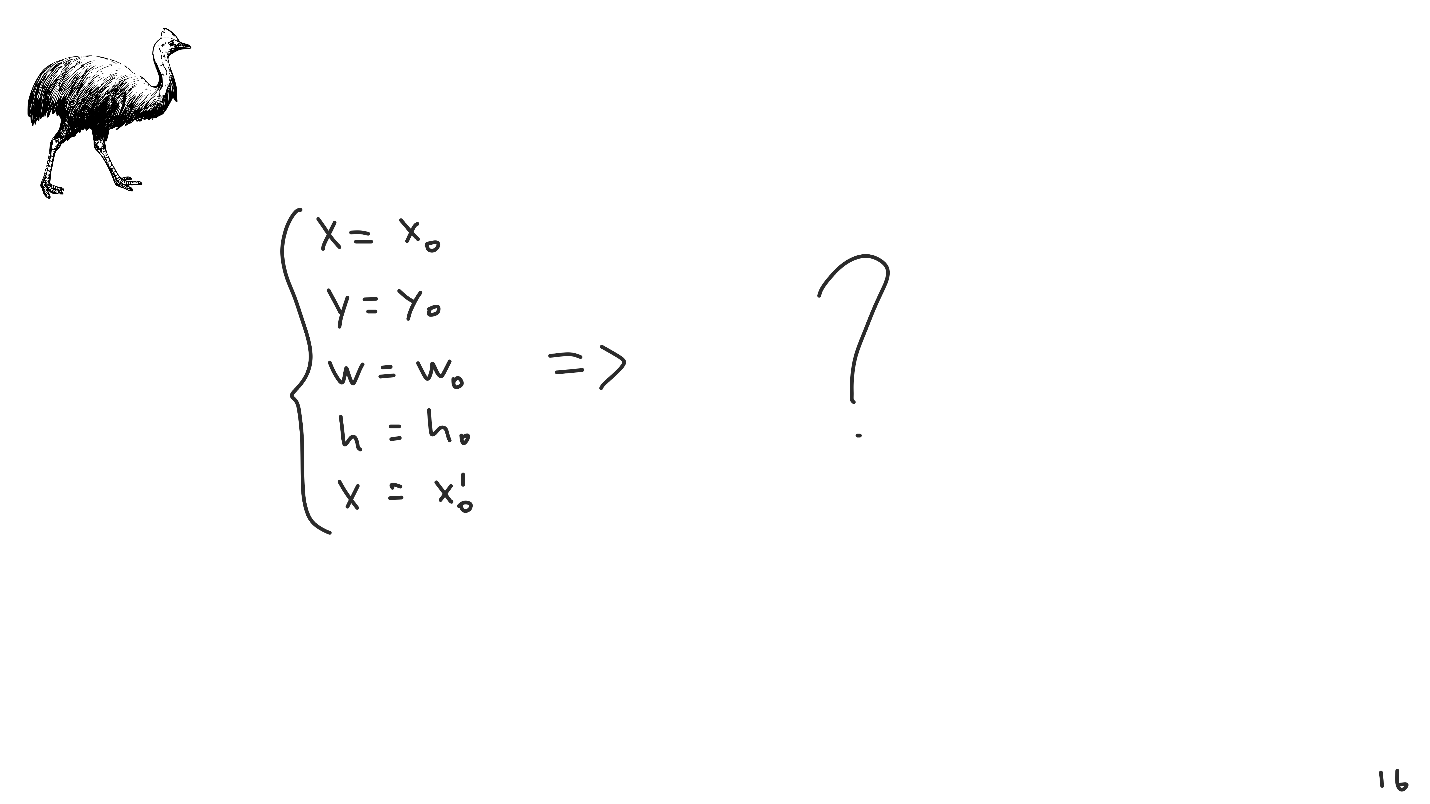
A problem appears - this system does not have a single solution. The problem is not exceptional, it is faced with absolutely all layout systems, and is called the lack of a solution .
There are not so many ways out of this situation:
Auto Layout. Setting and solving the problem
We have a rectangular picture and in order to uniquely identify it, we need 4 parameters:
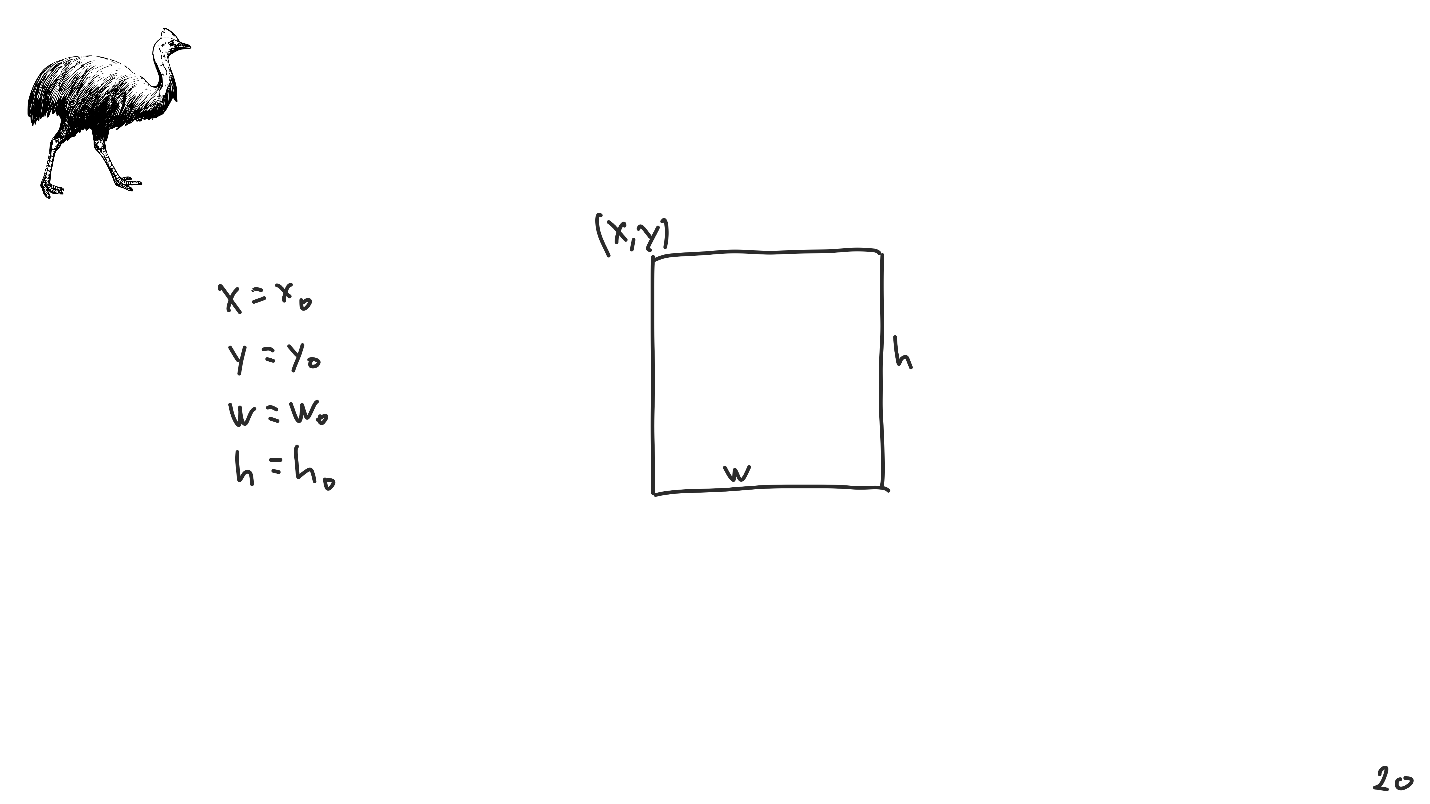
Auto Layout is very verbose. Compared to the system of linear equations, it is much more difficult to put everything on the screen with it. Therefore, we will consider, without losing generality, the one-dimensional case.

Everything is very simple: space is a straight line, and all the objects that can fit in it are points on a straight line. One value: X = X P is enough to determine the position of a point.
Consider the Auto Layout approach. There is a space in which restrictions are set. The solution we want to get is X = X 0 , and no other.
There is a problem - we have not defined operations with restrictions. We cannot directly infer from the record that X = X 0, we can not multiply anything and add with nothing. To do this, we need to convert the constraint into what we can work with - into a system of equations and inequalities.

Auto Layout converts the system of equations and inequalities as follows.
The point X 0 is the solution of the system: if a + and a - are equal to zero, then this will be true. But any other point on this line will be the solution.
Therefore, it is necessary to find the best among all the solutions. To do this, we introduce a functional — an ordinary function that returns a number, and we can compare numbers. Let's draw a graph and note that the solution we initially wanted to get is the minimum.
Got a linear programming problem . In this way, Auto Layout comes with restrictions that are not only in the form of equalities, but also inequalities.
Inequality constraints
In the case of inequality constraints, the transformation occurs in the same way as with equations: two additional variables are introduced and everything is assembled into the system. Only the functional is different, and it is equal to a - .

The graph above shows why this is so - any value of a + with a - = 0 (from X 0 to + ∞ ) will be the optimal solution for the problem.
Let's try to combine these two constraints of equations and inequalities into one thing - after all, the constraints do not live closed, they apply to the whole system together.

For each constraint, a pair of variables is additionally introduced, and a functional is composed. Since we want all these constraints to be fulfilled simultaneously, the functional will be equal to the sum of all functionals from each constraint .
We assemble the function f and see that the solution is X 1 . As we expected, making up restrictions. So we come to the third algorithm.
Algorithm number 3
To develop something, you need:
It seems that this algorithm is sufficient, but consider the following case: we change the initial set of constraints so that the second constraint is now X ≥ X 2 .

What solution do we expect to see?
To get out of the situation, we will perform transformations that we are already able to do.
The graph of the new functional looks different: any point from the interval from X 1 to X 2 will be the correct valid solution of the system. This is called uncertainty .
Uncertainty
Auto Layout has a mechanism for solving such problems - priorities . I remind you that yellow will indicate high priority, and blue - low.
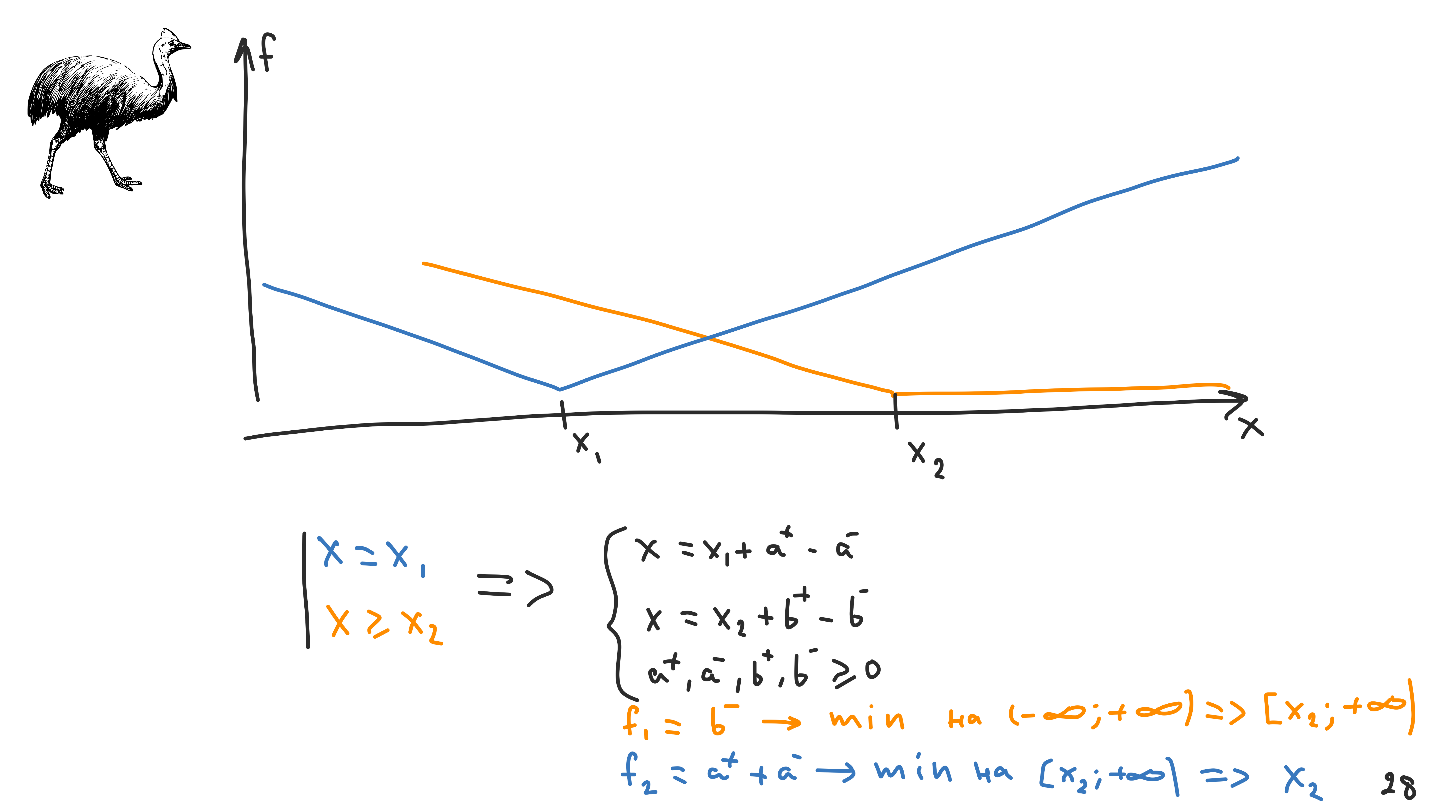
Convert constraints. Please note that the resulting system is just black. We know how to work with it, and there is no information about restrictions in it. It is in the functionals, of which there will be as many as two. Auto Layout will first minimize the first and then the second.
In linear programming problems, we are not looking for a solution itself, but an area of feasible solutions. Of course, we want this area to be only one point, and Auto Layout acts in the same way. First, it minimizes the highest priority functional on ( - ∞, + ∞)and the output gets the range of feasible solutions. The second linear programming problem Auto Layout solves already on the obtained range of acceptable values. Such a mechanism is called a hierarchy of constraints , and in this problem gives the point X 2 .
Algorithm number 4
Let's look at the previous task again. We are not mathematicians, but engineers, and any engineer should be confused here.
There is a serious problem - infinity , and I do not know what it is.
The Cassowary algorithm under the hood of Auto Layout was not an existing mechanism that conveniently lay down on the Auto Layout task, but was invented as a typesetting tool, and special mechanisms were provided to go from infinity at the very beginning. For this purpose several types of restrictions were invented:
Let's see how requirements with such priorities are transformed from the point of view of mathematics.

We again have a straight line with two points, and the first constraint is X = X 1 . On the slide, it is red, that is, this restriction with the priority of required - we will call it a requirement.
Auto Layout converts it to a linear equation system containing one equation X = X 1 . There is nothing more - no linear programming problems, no optimizations.
The situation is similar with inequalities, but a bit more complicated - an additional variable will appear .which can take any value greater than 0. For any value greater than 0, this restriction will be satisfied. Note that there are no linear programming and optimization problems here either.
Let's try to combine all this together, to collect two requirements and convert them into one system. The attentive reader, noted that we came to the same question from which we started - the requirements must be consistent .
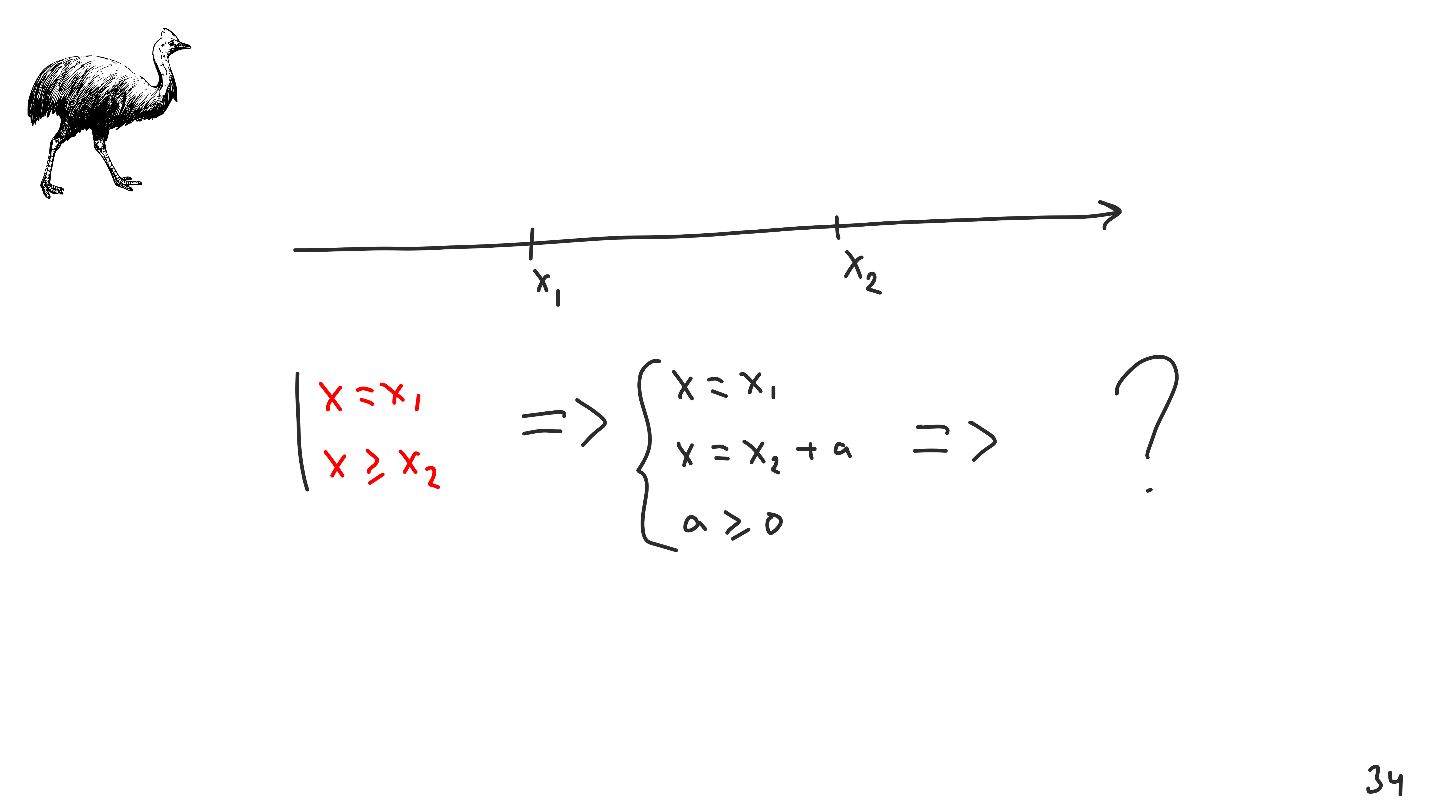
Restrictions like required or requirements are a very powerful tool, but not the main one, but an auxiliary one. It was specifically introduced in Auto Layout to solve the problem of infinite intervals, it should be used carefully.
Let's try to combine all types of restrictions with which we met in one system. Suppose we want to solve the problem not on the whole line, but only between X 0 and X 3 . Transforming all this into a system of linear equations and inequalities, we obtain the following.
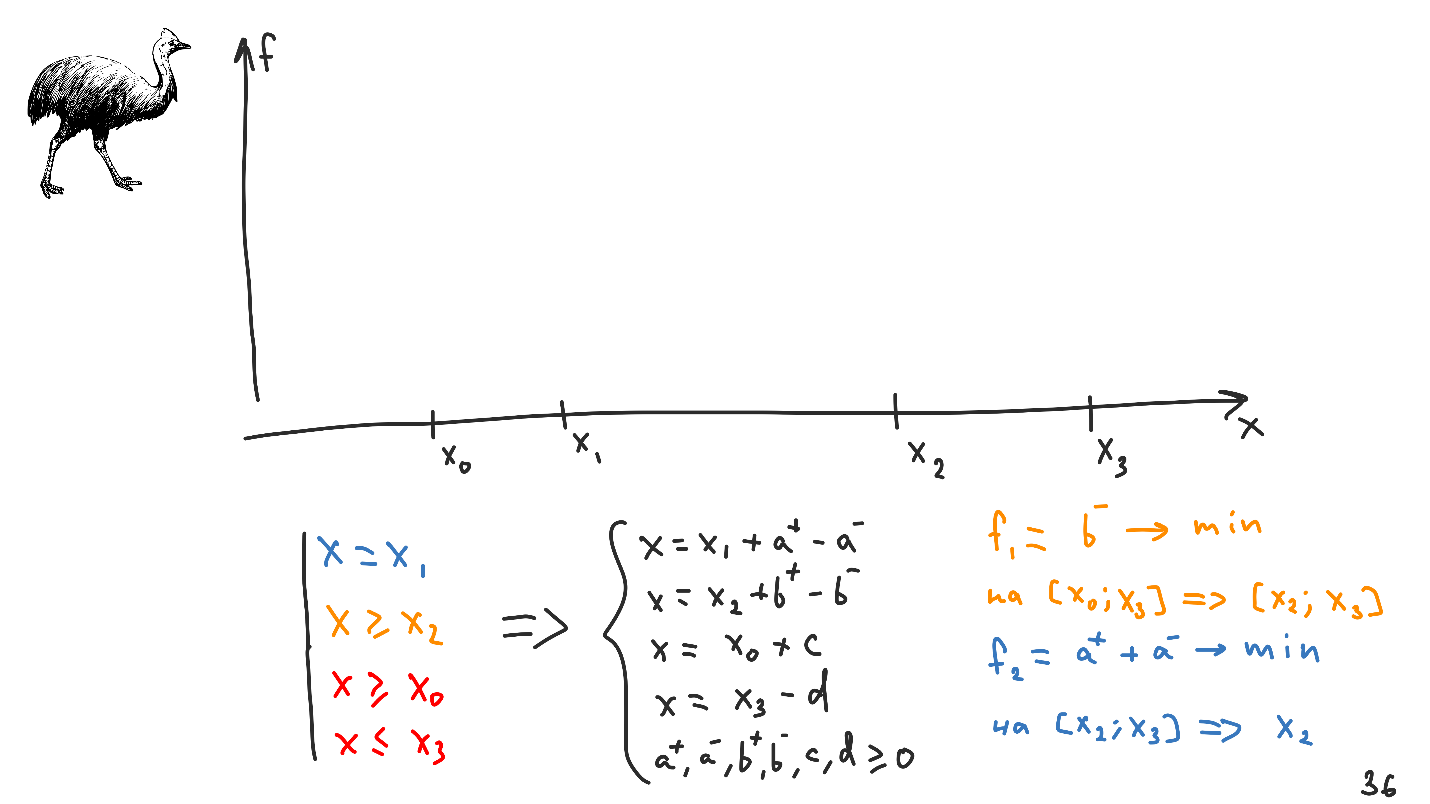
Regarding the previous system, two additional variables have been added - c and d , but they will not fall into the functionals, since the constraints of the required type do not affect the functionality in its original form.
It seems that the task has hardly changed - we minimize the same thing as before, but the initial range of acceptable values is changing, now it is from X 0 to X 3.
You need to be very careful with this, because excessive use of required constraints will lead to a problem without solutions , and Auto Layout cannot cope with it.
We arrive at the last fifth algorithm.
Algorithm number 5
We considered Cassowary, an algorithm that is inside Auto Layout, but when it is implemented, various features arise.
Features in iOS
There are no calculations in layoutSubviews () .
When are they produced? Answer: always, at any given time, Auto Layout is counted. The calculation takes place exactly when we add constraints to our view, or we activate them using modern API methods with constraints.
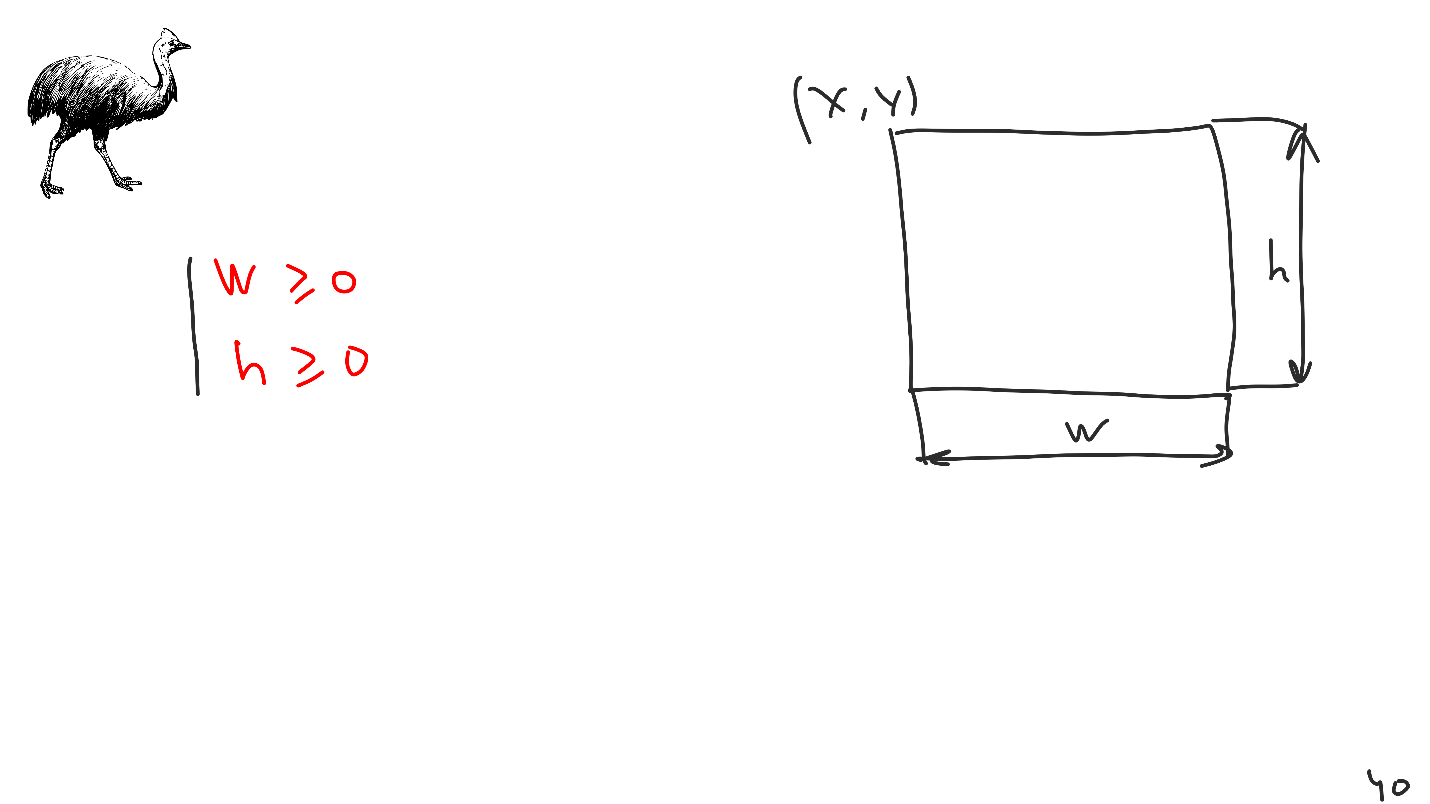
Our views are rectangles, but the problem is that inside Cazuar this information is not contained, it needs to be additionally inserted there. We have a mechanism for introducing additional restrictions. If we introduce for each view a set of restrictions with positive width and height, then at the output we will always get rectangles. That is why we can not impose with the help of Auto Layout view with negative dimensions.
The second feature is intrinsicContentSize - proper size that can be set for each view.
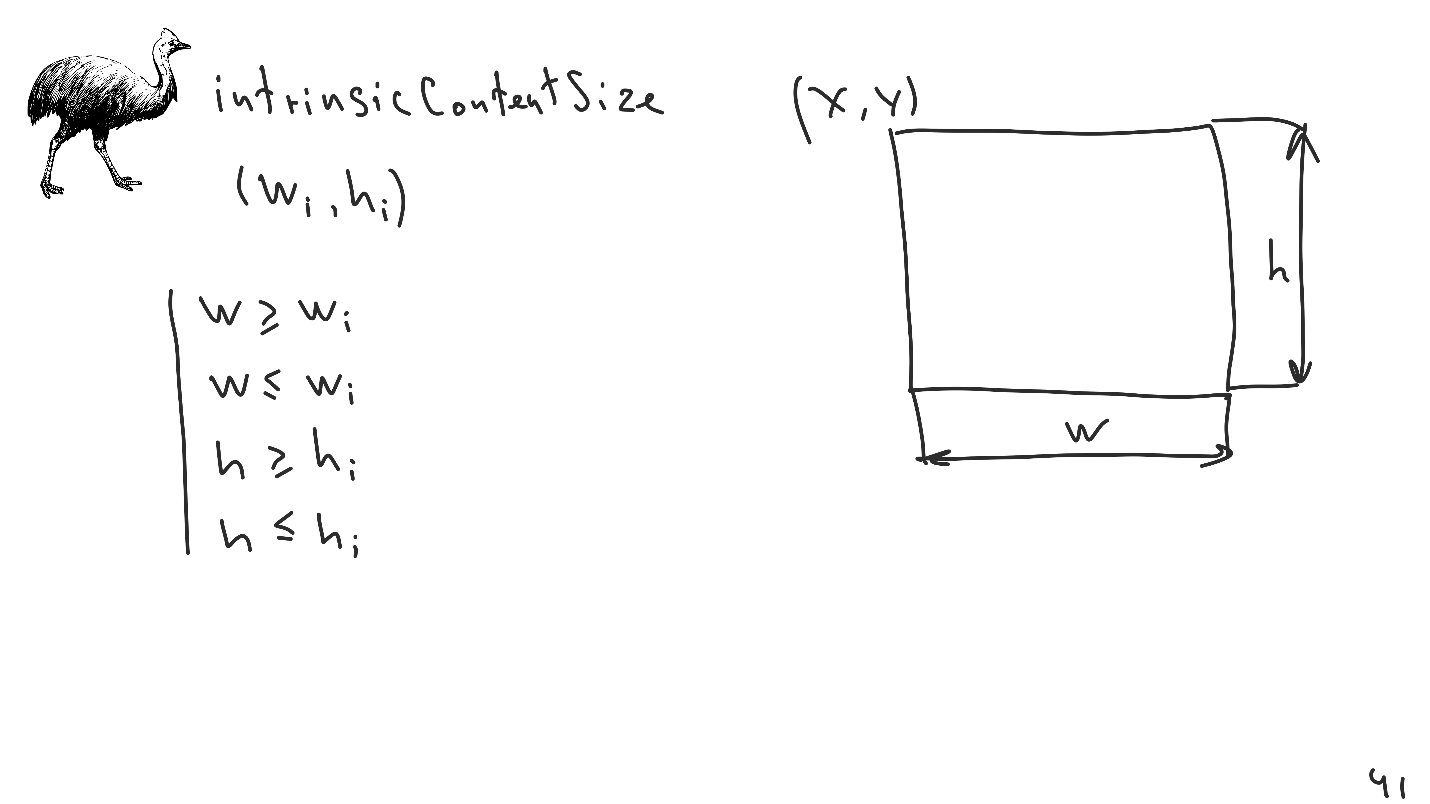
This is a simple interface for creating 4 additional inequality constraints to be placed in the system. This mechanism is very convenient, it allows you to reduce the number of explicit restrictions, which simplifies the use of Auto Layout. The last and most subtle point that people often forget about is TranslateAutoresizingMaskIntoConstraints.
This is a crutch, which was introduced at the time of iOS 5, so that the old code after the appearance of Auto Layout does not break.
Imagine the situation: we impose view on constraints. Inside the view, we use the view, which knows nothing about constraints, imposes everything on the frames, but inside it, it imposes a view, which has long been transferred to constraints.
The size and position of the view that was rendered on frames is not completely determined by constraints. When calculating the size and position of all other views, incorrect sizes will be taken into account, even though after Auto Layout we will apply the correct frames there.
To avoid this situation, if the value of the TranslateAutoresizingMaskIntoConstraints variable is true, then an additional restriction is implemented for each view that is imposed on the frame. This set of restrictions may differ from run to run. Only one thing is known about this set: the frame that was transmitted will be its solution.
Compatibility of old code written without constraints and new one written with constraints can often suffer due to improper use of this property. These constraints necessarily take precedence of requirements, so if we suddenly place constraints on such a view, which have a very high priority, for example, a requirement, we can accidentally create a non-consistent system that will not have solutions.
It is important to know:
The idea is very simple - the old code, in which the view was created, did not know anything about Auto Layout, and it was necessary to make it so that if the view was used somewhere in a new place, then it would work.
Practical advice
Total council will be three and begin with the most important.
Optimization
Have you ever encountered the problem of optimizing the screen, which is laid out on the Auto Layout? Most likely not, more often you are faced with the problem of optimizing the layout of cells within a table or a Collection View .
Auto Layout is optimized enough to impose any screen and any interface, but to impose 50 or 100 at once is a problem for it. To localize and optimize it, let's look at the experiment. Figures are taken from the article where Kazuar was first described.

The task is this: create a view chain one by one, and connect each subsequent one with the previous one. Thus, a sequence of 1000 elements was lined up. After various operations were measured, the time is specified in milliseconds. The values are quite large, because Auto Layout was invented at the junction of the 80s and 90s.
Collecting such a chain, you can act as follows:
The first two points can be described as the primary calculation of interfaces, the last two - as the next one.
Primary interface calculation
Here you can use the methods of mass adding constraints for optimization:
Subsequent interface calculations
Adding or changing constraint is a complicated operation, so it’s better not to change the set of constraints, but to change only the constants in the existing constraints. For this there are the following techniques:
To get acquainted in detail with the techniques, I advise you to watch the session WWDC 2018S220 High Performance Auto Layout . It is unique - Apple is deeply involved in the implementation and describes many convenient mechanisms that allow you to create cells optimally.
Design constraints
Next I will give some practical tips that can help in working with constraints.
Start with priorities
The more required restrictions, requirements - the greater the likelihood that you will one day come to an inconsistent system that will not have a solution. You have problems.
Here are very simple rules:
Freeze requirements
We all know that walking on water and working on demand is equally easy when they are frozen.
When you create constraint with the required priority, do not change it in runtime . If it needs to be changed, it means that you made a mistake in the design, and in fact this is not a requirement. Redefine your system so that you can change optional restrictions.
Obvious conclusion - the lower the priority, the cheaper the modification of the restriction. This directly proceeds from the fact that tasks in the hierarchy of priorities are solved sequentially - from higher priority to low priority ones. If we change something in low priority, then the decision of the upper ones will not affect in any way, and the range of acceptable values will not change. Auto Layout understands this and solves the system optimally if you change only low-priority constraints.
Accidentally creating conflicting requirements is extremely easy if you change them in runtime. You may not even notice. Moreover, this may not be your final point, when the requirements will become priorities, but only an intermediate one. As a result, you build the same layout, but the situation when the system is not solvable is extremely expensive in terms of performance. Therefore, it is better to avoid it at the design stage.
Use inequalities
Inequality is a cool tool that allows you to use Auto Layout, since we cannot use many other typesetting systems, and it is simply wrong to ignore them.
The advantages of inequality, such as required, are that it is much more difficult to create contradictions with them . Receptions are quite simple:
The most important thing that I wanted to convey in this article is an understanding of how we come to limitations .
We first transformed the requirements into a system of linear equations and came up with problems, and then went a completely different way. Therefore, when problems or bugs arise, we try to analyze them from the point of view of a system of linear equations, and try to solve it. This is not true; restrictions are not equations . It is wrong to approach them in this way.
Requirements and parameters are fundamentally different things.We are used to working with constraints as if they were just different priorities, but it is important to understand and remember that it is important - both from the point of view of mathematics, and inside when solving - the required type and all the others are solved in fundamentally different ways.
Useful links:
Solving in brief Solving the Linear Arithmetic the Constraints for the User Interface the Applications
of The Cassowary the Linear of Constraint Solving in brief Solving the Algorithm
the Constraints as with the Design Pattern A s
the Auto Guide Review the Layout by Apple's
the WWDC 2018 Session 220 High Performance Auto Layout
Magic UILabel or private API Auto Layout - Alexander Goremykin
Blog on Yandex.Maps Medium
But perhaps the reason is not outside, but inside. For example, the world's most dangerous birds will not attack people for no reason, just for the sake of self-defense. Therefore, try for a second to assume that this is not Auto Layout is bad, and you do not understand it well enough and do not know how to cook. So did Anton Sergeyev and dive into the theory in order to understand everything precisely. We are offered a finished squeeze about the mathematical foundations of Auto Layout.

Auto Layout is a layout system . Before delving into it, let's talk about modern layout in general. Then we will deal with Auto Layout - let's figure out what problem it solves and how it does it. Consider the features in the implementation of Auto Layout in iOS , and try to develop practical tips that can help you work with it.
This story will be very close to a mathematical article, so we first agree on the notation in order to speak the same language.
About the speaker: Anton Sergeev ( antonsergeev88 ) works in the Yandex.Maps team, deals with a mobile client for Maps on iOS. Prior to mobile development, he was in charge of power plant control systems, where the price of errors in the code is too high to be tolerated.
Legend
Systems of linear equations are familiar to us from school — indicated by a curly bracket, and their solution is already without. Also, systems of linear equations have entities with which Auto Layout operates - restrictions. Denoted by a straight line.
A strange and, as we already know, dangerous bird is not accidentally drawn in the upper corner of the slide. In honor of the cassowary (lat. Cassowary), which, of course, lives in Australia, an algorithm is named in all our iPhones.
In Auto Layout there are limitations, we will designate them with colors in order of priority: red - required; yellow - high; blue - low.
Layout
When I made the presentation, I had various elements on the screen, for example, cassowary. To do this, I determined that the cazuar is a rectangular picture. You need to place it on a sheet that has axes and its coordinate system, and for this I determined the coordinates of the upper left corner, width and height.

Knowing these four values is enough to present any View.
Algorithm number 1
While we had cassowary on a sheet, we unobtrusively described the first layout algorithm:
- determine the coordinates and sizes;
- apply them to a UIView.
The algorithm works, but is rather complicated to use, so we will further simplify it.
Suppose that below - the solution of some system of linear equations.
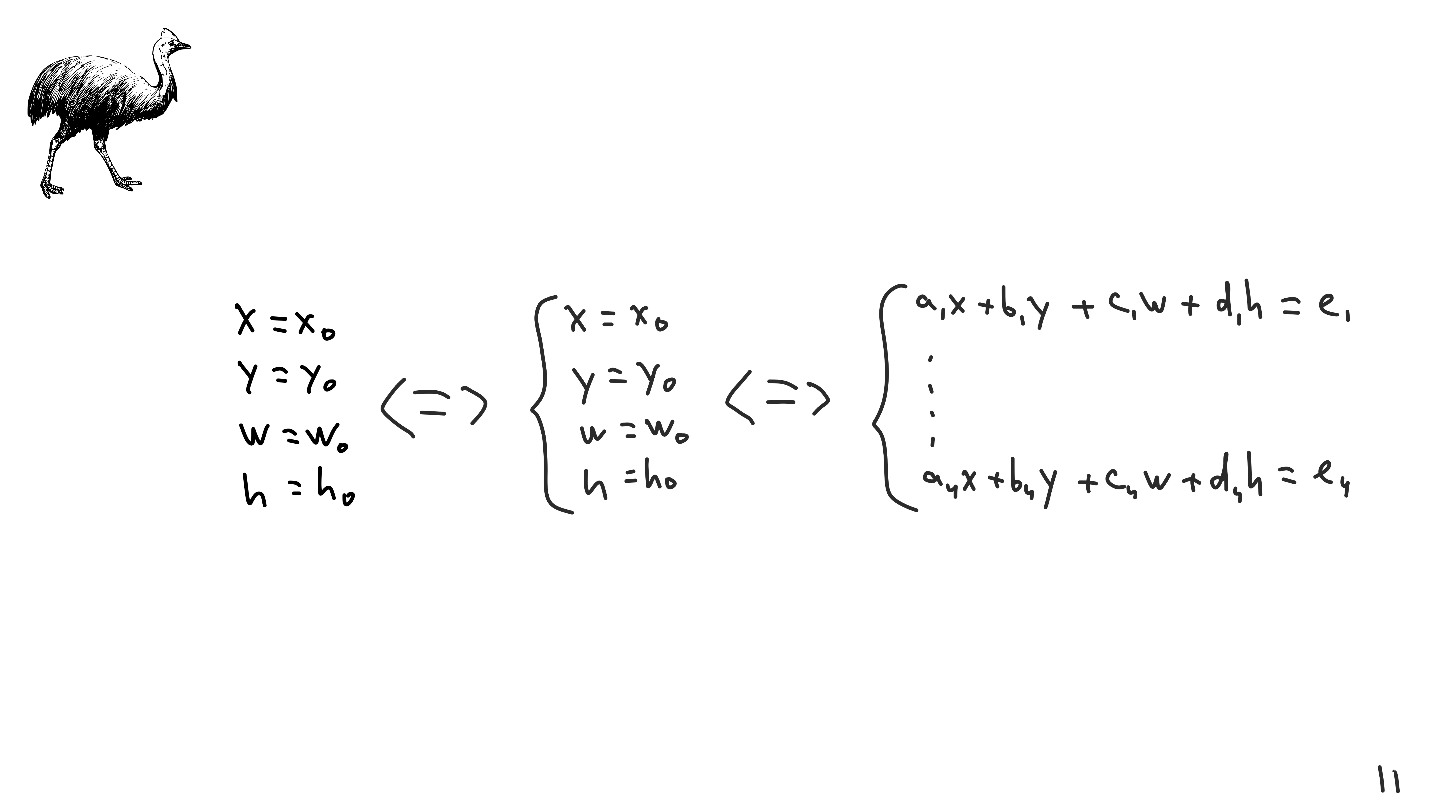
The system of linear equations is special in that a mass of operations is defined above it: folding the lines, multiplying them by constants, etc. These operations are called linear transformations, and with their help the system is reduced to an arbitrary form.
The beauty of linear transformations is that they are reversible. This brings us to an interesting and rather subtle idea, from which the whole modern layout begins.
Let there is a View - a rectangle with its own coordinates and size. We want to arrange it so that the center coincides with the given point. We will model the center using linear transformations -coordinate of the upper left corner + half width .

We modeled the center by a linear transformation, it was not there: there were only the coordinates of the left upper point, the width and height.
Similarly, you can simulate any other indents, for example, 20 points from the right corner.
It is the idea of linear transformations that allows us to create different typesetting systems.
Consider an elementary example. We write out a system with which we establish the coordinates of the middle and right side, the width and the ratio between width and height. We solve the system and get an answer.
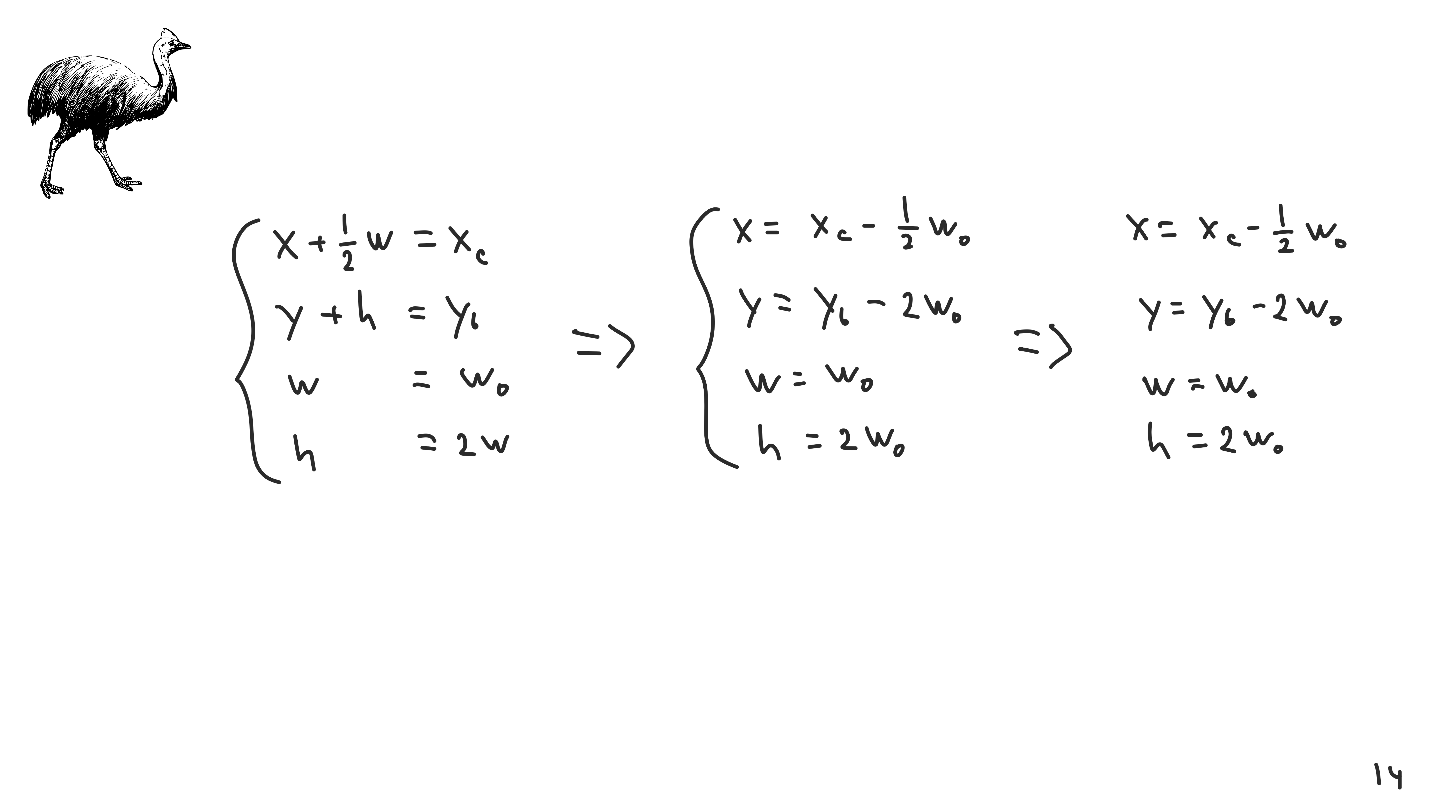
So we come to the second algorithm.
Algorithm number 2
The second iteration of the algorithm consists of the following items:
- draw up a system of linear equations;
- we solve it;
- apply the solution to a UIView.
Imagine that we were in the twentieth century, at a time when computer technology was just emerging, and were the first to reach the creation of our typesetting system. Invented, packed, given to the user, and he begins to use it - fills in the initial parameters and transmits to our system.
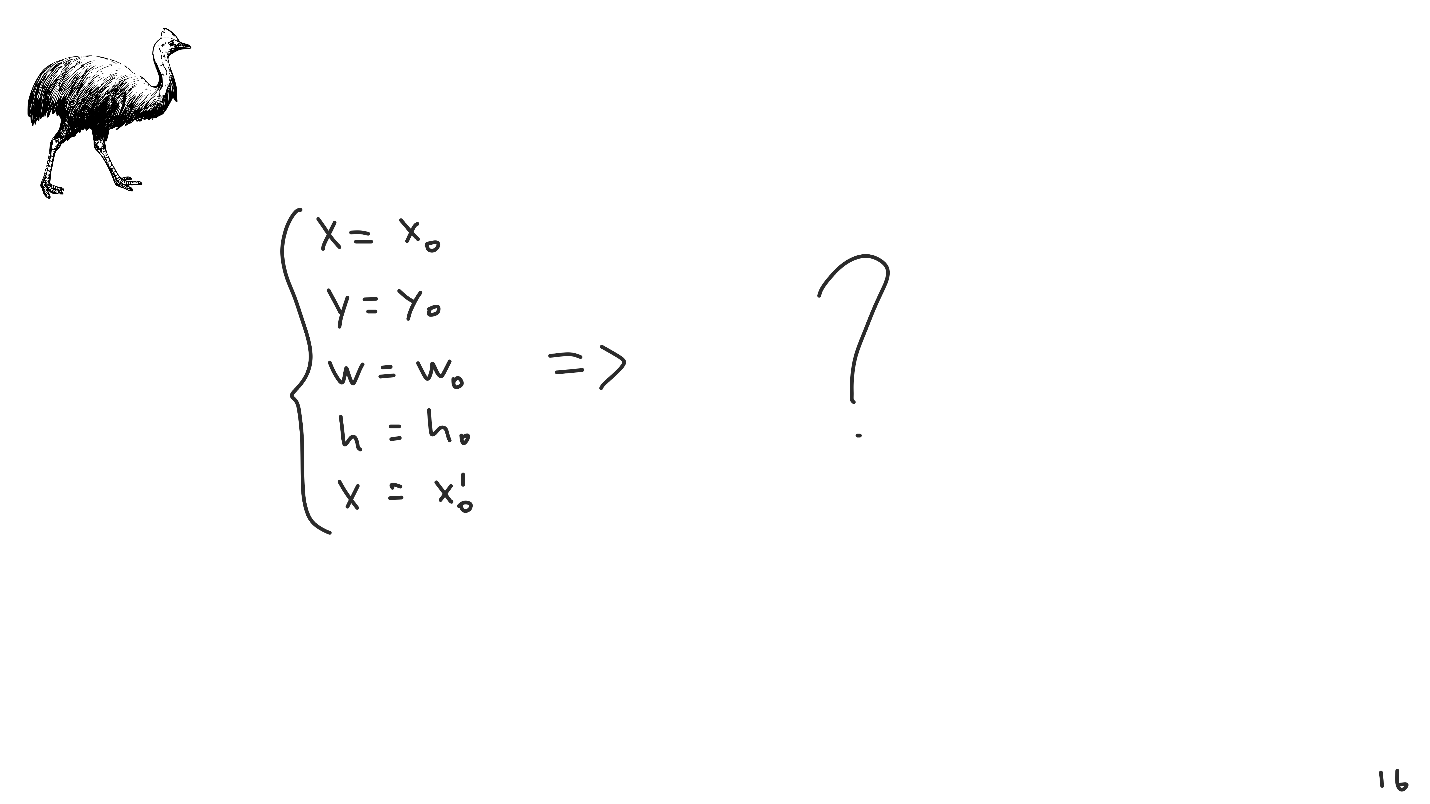
A problem appears - this system does not have a single solution. The problem is not exceptional, it is faced with absolutely all layout systems, and is called the lack of a solution .
There are not so many ways out of this situation:
- You can fall - this is a very common method. Who works with MacOS, knows that NSLayoutConstraintManager does this.
- Return the default value . In the context of the layout, we can always return all zeros.
- A more well-known and delicate way is to prevent incorrect input . This method is used by popular typesetting systems, for example, Yoga , known as Flex Layout . Such systems try to create an interface that will not allow incorrect input.
- There is another way to solve absolutely all problems - it is to rethink everything from the very beginning and initially prevent this problem from occurring . Auto Layout went this way.
Auto Layout. Setting and solving the problem
We have a rectangular picture and in order to uniquely identify it, we need 4 parameters:
- coordinates of the upper left corner;
- width and height.

Auto Layout is very verbose. Compared to the system of linear equations, it is much more difficult to put everything on the screen with it. Therefore, we will consider, without losing generality, the one-dimensional case.

Everything is very simple: space is a straight line, and all the objects that can fit in it are points on a straight line. One value: X = X P is enough to determine the position of a point.
Consider the Auto Layout approach. There is a space in which restrictions are set. The solution we want to get is X = X 0 , and no other.
There is a problem - we have not defined operations with restrictions. We cannot directly infer from the record that X = X 0, we can not multiply anything and add with nothing. To do this, we need to convert the constraint into what we can work with - into a system of equations and inequalities.

Auto Layout converts the system of equations and inequalities as follows.
- First introduces 2 additional variables that are not negative and depend on each other . At least one of them is zero.
- The constraint itself is converted to the record X = X 0 + a + - a - .
The point X 0 is the solution of the system: if a + and a - are equal to zero, then this will be true. But any other point on this line will be the solution.
Therefore, it is necessary to find the best among all the solutions. To do this, we introduce a functional — an ordinary function that returns a number, and we can compare numbers. Let's draw a graph and note that the solution we initially wanted to get is the minimum.
Got a linear programming problem . In this way, Auto Layout comes with restrictions that are not only in the form of equalities, but also inequalities.
Inequality constraints
In the case of inequality constraints, the transformation occurs in the same way as with equations: two additional variables are introduced and everything is assembled into the system. Only the functional is different, and it is equal to a - .

The graph above shows why this is so - any value of a + with a - = 0 (from X 0 to + ∞ ) will be the optimal solution for the problem.
Let's try to combine these two constraints of equations and inequalities into one thing - after all, the constraints do not live closed, they apply to the whole system together.

For each constraint, a pair of variables is additionally introduced, and a functional is composed. Since we want all these constraints to be fulfilled simultaneously, the functional will be equal to the sum of all functionals from each constraint .
We assemble the function f and see that the solution is X 1 . As we expected, making up restrictions. So we come to the third algorithm.
Algorithm number 3
To develop something, you need:
- create a system of linear constraints;
- convert it to a linear programming problem;
- solve the problem by any known method, for example, by the simplex method used in Auto Layout;
- apply the solution to a UIView.
It seems that this algorithm is sufficient, but consider the following case: we change the initial set of constraints so that the second constraint is now X ≥ X 2 .

What solution do we expect to see?
- X 1 ? Indeed, in the first constraint it is written this way: X = X 1 , and this solution conflicts with the second constraint.
- X 2 ? There will be a conflict with the first limitation.
To get out of the situation, we will perform transformations that we are already able to do.
The graph of the new functional looks different: any point from the interval from X 1 to X 2 will be the correct valid solution of the system. This is called uncertainty .
Uncertainty
Auto Layout has a mechanism for solving such problems - priorities . I remind you that yellow will indicate high priority, and blue - low.
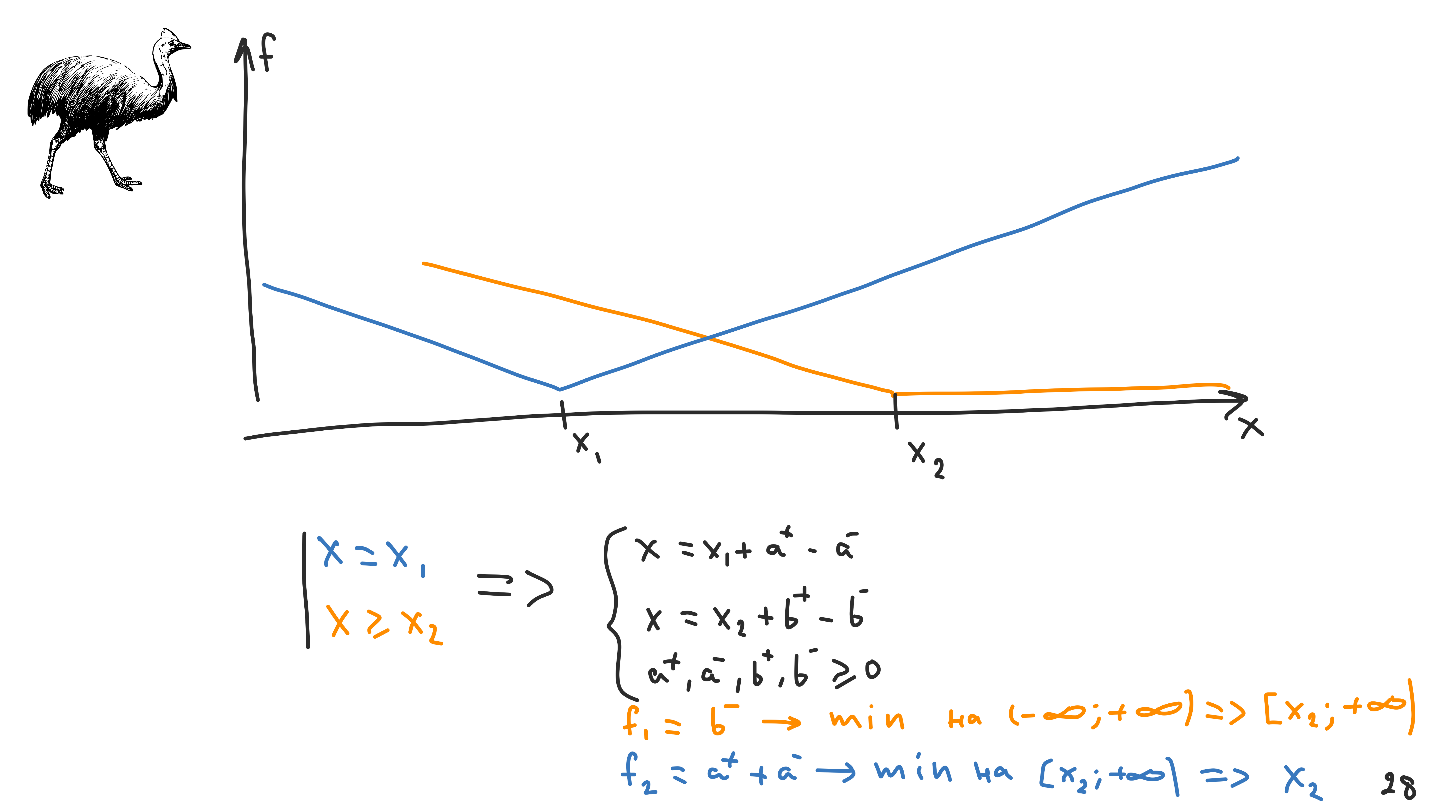
Convert constraints. Please note that the resulting system is just black. We know how to work with it, and there is no information about restrictions in it. It is in the functionals, of which there will be as many as two. Auto Layout will first minimize the first and then the second.
In linear programming problems, we are not looking for a solution itself, but an area of feasible solutions. Of course, we want this area to be only one point, and Auto Layout acts in the same way. First, it minimizes the highest priority functional on ( - ∞, + ∞)and the output gets the range of feasible solutions. The second linear programming problem Auto Layout solves already on the obtained range of acceptable values. Such a mechanism is called a hierarchy of constraints , and in this problem gives the point X 2 .
Algorithm number 4
- Create a hierarchy of linear constraints;
- convert it to a linear programming problem;
- Solve the linear programming problem sequentially, from the highest priority to the lowest priority.
- apply the solution to ulview.
Let's look at the previous task again. We are not mathematicians, but engineers, and any engineer should be confused here.
There is a serious problem - infinity , and I do not know what it is.
The Cassowary algorithm under the hood of Auto Layout was not an existing mechanism that conveniently lay down on the Auto Layout task, but was invented as a typesetting tool, and special mechanisms were provided to go from infinity at the very beginning. For this purpose several types of restrictions were invented:
- Parameters - these are the limitations with which we worked. In the original, they are called preferences, sometimes in the Apple documentation - optional constraints .
- Requirements or requirements - restrictions with priority required .
Let's see how requirements with such priorities are transformed from the point of view of mathematics.

We again have a straight line with two points, and the first constraint is X = X 1 . On the slide, it is red, that is, this restriction with the priority of required - we will call it a requirement.
Auto Layout converts it to a linear equation system containing one equation X = X 1 . There is nothing more - no linear programming problems, no optimizations.
The situation is similar with inequalities, but a bit more complicated - an additional variable will appear .which can take any value greater than 0. For any value greater than 0, this restriction will be satisfied. Note that there are no linear programming and optimization problems here either.
Let's try to combine all this together, to collect two requirements and convert them into one system. The attentive reader, noted that we came to the same question from which we started - the requirements must be consistent .

Restrictions like required or requirements are a very powerful tool, but not the main one, but an auxiliary one. It was specifically introduced in Auto Layout to solve the problem of infinite intervals, it should be used carefully.
Let's try to combine all types of restrictions with which we met in one system. Suppose we want to solve the problem not on the whole line, but only between X 0 and X 3 . Transforming all this into a system of linear equations and inequalities, we obtain the following.
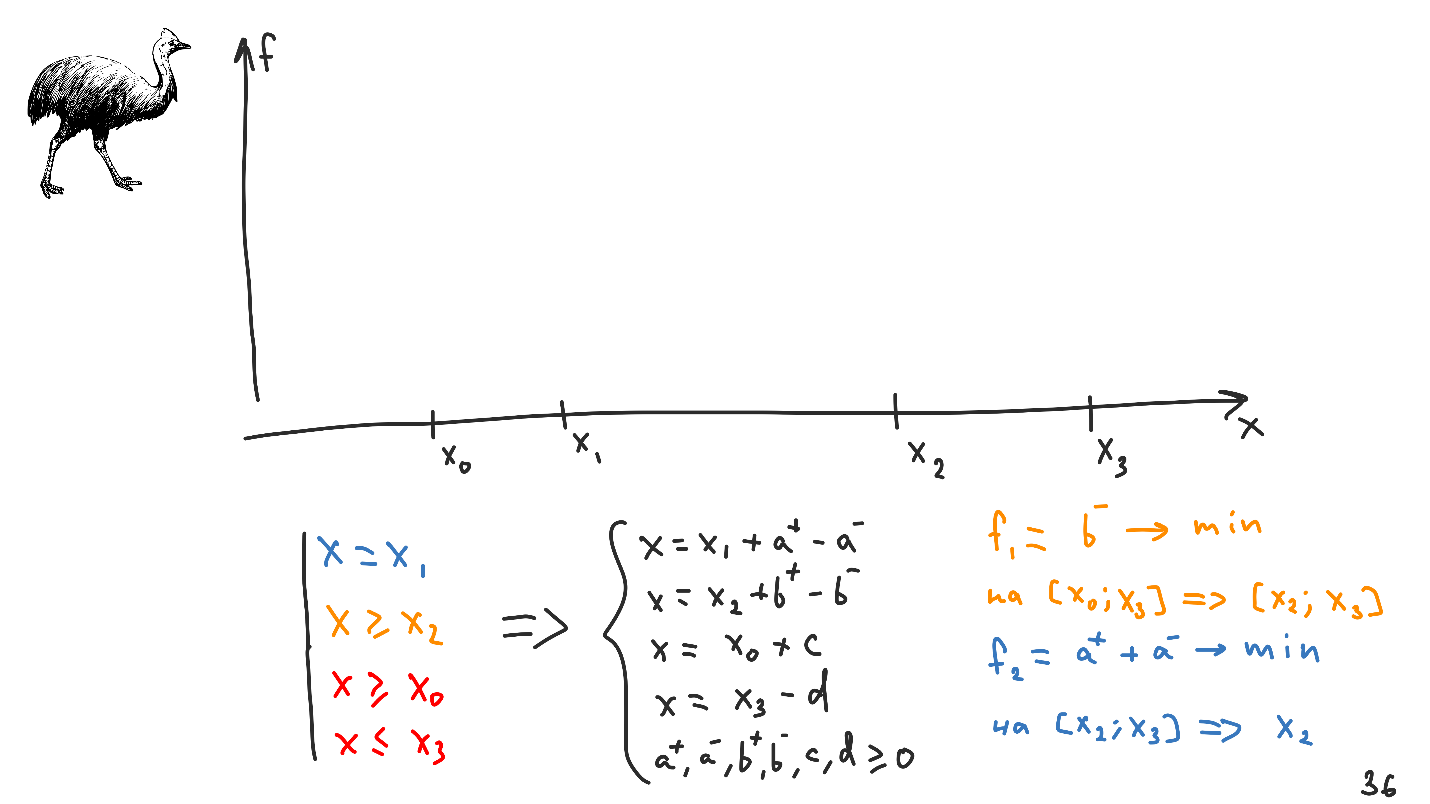
Regarding the previous system, two additional variables have been added - c and d , but they will not fall into the functionals, since the constraints of the required type do not affect the functionality in its original form.
It seems that the task has hardly changed - we minimize the same thing as before, but the initial range of acceptable values is changing, now it is from X 0 to X 3.
From a mathematical point of view, the requirements — constraints of the type required — are the ability to introduce additional equations into the system without modifying its functionals.
You need to be very careful with this, because excessive use of required constraints will lead to a problem without solutions , and Auto Layout cannot cope with it.
We arrive at the last fifth algorithm.
Algorithm number 5
- Identify the necessary restrictions - layout requirements;
- create a hierarchy of linear constraints;
- convert all constraints into a linear programming problem;
- solve the problem of linear programming;
- apply the solution to ulview.
We considered Cassowary, an algorithm that is inside Auto Layout, but when it is implemented, various features arise.
Features in iOS
There are no calculations in layoutSubviews () .
When are they produced? Answer: always, at any given time, Auto Layout is counted. The calculation takes place exactly when we add constraints to our view, or we activate them using modern API methods with constraints.

Our views are rectangles, but the problem is that inside Cazuar this information is not contained, it needs to be additionally inserted there. We have a mechanism for introducing additional restrictions. If we introduce for each view a set of restrictions with positive width and height, then at the output we will always get rectangles. That is why we can not impose with the help of Auto Layout view with negative dimensions.
The second feature is intrinsicContentSize - proper size that can be set for each view.

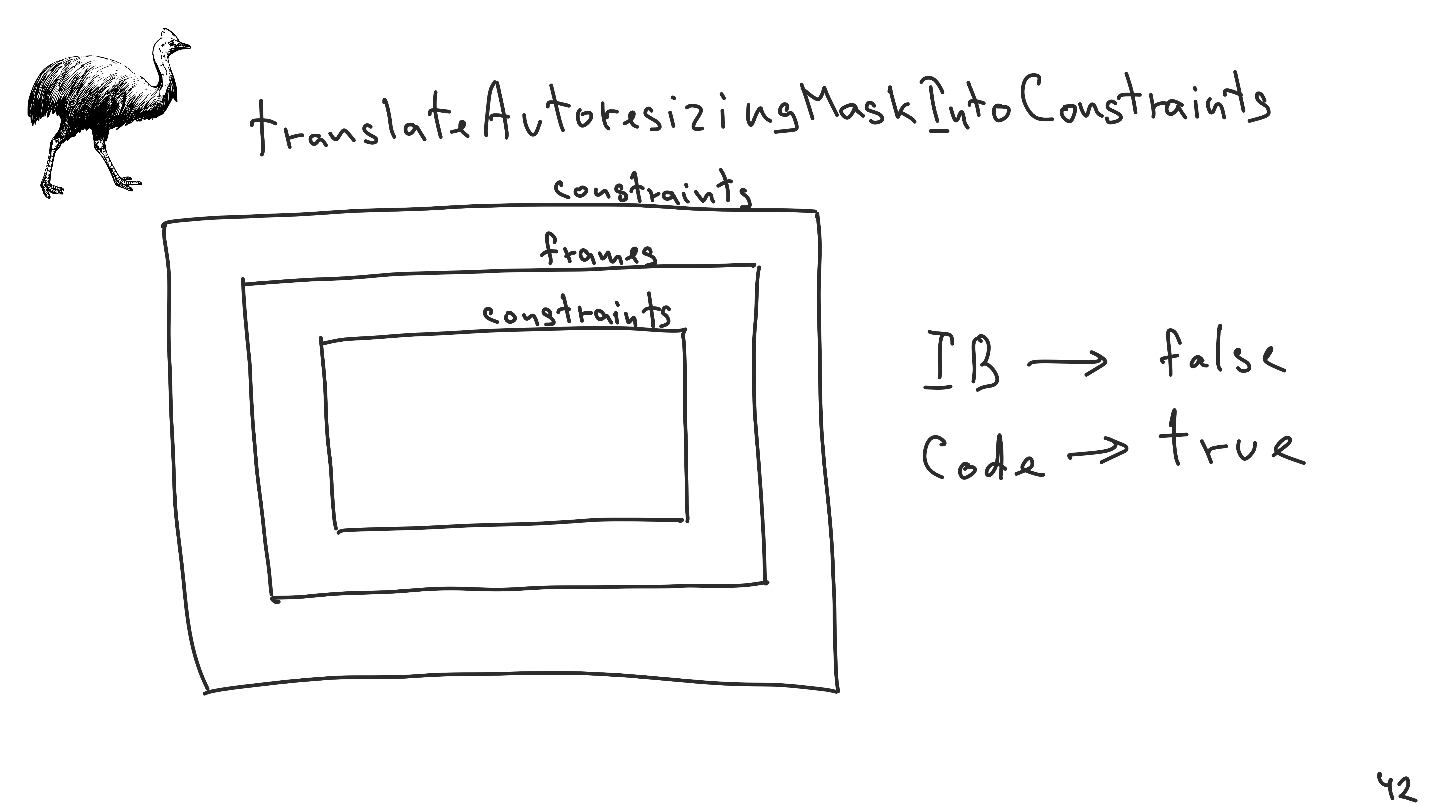
This is a simple interface for creating 4 additional inequality constraints to be placed in the system. This mechanism is very convenient, it allows you to reduce the number of explicit restrictions, which simplifies the use of Auto Layout. The last and most subtle point that people often forget about is TranslateAutoresizingMaskIntoConstraints.

This is a crutch, which was introduced at the time of iOS 5, so that the old code after the appearance of Auto Layout does not break.
Imagine the situation: we impose view on constraints. Inside the view, we use the view, which knows nothing about constraints, imposes everything on the frames, but inside it, it imposes a view, which has long been transferred to constraints.
I remind you that there are no frames inside the Kasuar Auto Layout task, only frames.
The size and position of the view that was rendered on frames is not completely determined by constraints. When calculating the size and position of all other views, incorrect sizes will be taken into account, even though after Auto Layout we will apply the correct frames there.
To avoid this situation, if the value of the TranslateAutoresizingMaskIntoConstraints variable is true, then an additional restriction is implemented for each view that is imposed on the frame. This set of restrictions may differ from run to run. Only one thing is known about this set: the frame that was transmitted will be its solution.
Compatibility of old code written without constraints and new one written with constraints can often suffer due to improper use of this property. These constraints necessarily take precedence of requirements, so if we suddenly place constraints on such a view, which have a very high priority, for example, a requirement, we can accidentally create a non-consistent system that will not have solutions.
It is important to know:
- If we create a view from Interface Builder , then the default value for this property will be false .
- If we create a view directly from the code, then it will be true .
The idea is very simple - the old code, in which the view was created, did not know anything about Auto Layout, and it was necessary to make it so that if the view was used somewhere in a new place, then it would work.
Practical advice
Total council will be three and begin with the most important.
Optimization
It is important to isolate the problem.
Have you ever encountered the problem of optimizing the screen, which is laid out on the Auto Layout? Most likely not, more often you are faced with the problem of optimizing the layout of cells within a table or a Collection View .
Auto Layout is optimized enough to impose any screen and any interface, but to impose 50 or 100 at once is a problem for it. To localize and optimize it, let's look at the experiment. Figures are taken from the article where Kazuar was first described.

The task is this: create a view chain one by one, and connect each subsequent one with the previous one. Thus, a sequence of 1000 elements was lined up. After various operations were measured, the time is specified in milliseconds. The values are quite large, because Auto Layout was invented at the junction of the 80s and 90s.
Collecting such a chain, you can act as follows:
- Consistently add one constraint and solve each time. This will take 38 seconds.
- You can add all the restrictions at once at a time , and only then decide the system. This solution is more efficient. According to the old data, the efficiency increases by 70%, but in the current implementation on modern devices there will be only 20%. But qualitatively one-time addition of restrictions will always be more effective.
- When the whole chain is assembled, you can add another constraint . As can be seen from the table, this operation is quite cheap.
- The most interesting thing: if we do not add any new restrictions, but change some constant in one of the existing ones , this is an order of magnitude more efficient than deleting or creating a new restriction.
The first two points can be described as the primary calculation of interfaces, the last two - as the next one.
Primary interface calculation
Here you can use the methods of mass adding constraints for optimization:
- NSLayoutConstraints.activate (_ :) - when creating a view, collect all the constraints in sequence into an array, cache and then add one at a time.
- Or create cells in the Interface Builder. He will do everything for us, and will carry out additional optimization, which is often convenient.
Subsequent interface calculations
Adding or changing constraint is a complicated operation, so it’s better not to change the set of constraints, but to change only the constants in the existing constraints. For this there are the following techniques:
- Hide UIView - the most interesting and underused technique. When you delete a view, the entire cache that was saved in Auto Layout is cleared. If we just hide it, the cache will not be erased, but at the same time you can impose a view that will have a different display.
- Manage priorities for intrinsic constraints - IntrinsicContentSize. An effective method that allows you to cope well with cells, but is often forgotten about it.
- Create more cell types . If your cells are very different from one another, they may be of different types.
To get acquainted in detail with the techniques, I advise you to watch the session WWDC 2018S220 High Performance Auto Layout . It is unique - Apple is deeply involved in the implementation and describes many convenient mechanisms that allow you to create cells optimally.
Design constraints
Next I will give some practical tips that can help in working with constraints.
Start with priorities
The more required restrictions, requirements - the greater the likelihood that you will one day come to an inconsistent system that will not have a solution. You have problems.
In any incomprehensible situation, lower the priority, no matter what happens.
Here are very simple rules:
- The smaller the components, the greater the priorities . The less you impose a component (button or loader) - the higher should be the priority.
- The larger the components, the lower the priorities . If you make a huge screen, then the priorities should be low.
Freeze requirements
We all know that walking on water and working on demand is equally easy when they are frozen.
When you create constraint with the required priority, do not change it in runtime . If it needs to be changed, it means that you made a mistake in the design, and in fact this is not a requirement. Redefine your system so that you can change optional restrictions.
Obvious conclusion - the lower the priority, the cheaper the modification of the restriction. This directly proceeds from the fact that tasks in the hierarchy of priorities are solved sequentially - from higher priority to low priority ones. If we change something in low priority, then the decision of the upper ones will not affect in any way, and the range of acceptable values will not change. Auto Layout understands this and solves the system optimally if you change only low-priority constraints.
Accidentally creating conflicting requirements is extremely easy if you change them in runtime. You may not even notice. Moreover, this may not be your final point, when the requirements will become priorities, but only an intermediate one. As a result, you build the same layout, but the situation when the system is not solvable is extremely expensive in terms of performance. Therefore, it is better to avoid it at the design stage.
Use inequalities
Inequality is a cool tool that allows you to use Auto Layout, since we cannot use many other typesetting systems, and it is simply wrong to ignore them.
The advantages of inequality, such as required, are that it is much more difficult to create contradictions with them . Receptions are quite simple:
- The higher the priority, the greater the inequalities should be.
- Conversely, the lower the priority, the more equalities can be used.
The most important thing that I wanted to convey in this article is an understanding of how we come to limitations .
We first transformed the requirements into a system of linear equations and came up with problems, and then went a completely different way. Therefore, when problems or bugs arise, we try to analyze them from the point of view of a system of linear equations, and try to solve it. This is not true; restrictions are not equations . It is wrong to approach them in this way.
Requirements and parameters are fundamentally different things.We are used to working with constraints as if they were just different priorities, but it is important to understand and remember that it is important - both from the point of view of mathematics, and inside when solving - the required type and all the others are solved in fundamentally different ways.
Useful links:
Solving in brief Solving the Linear Arithmetic the Constraints for the User Interface the Applications
of The Cassowary the Linear of Constraint Solving in brief Solving the Algorithm
the Constraints as with the Design Pattern A s
the Auto Guide Review the Layout by Apple's
the WWDC 2018 Session 220 High Performance Auto Layout
Magic UILabel or private API Auto Layout - Alexander Goremykin
Blog on Yandex.Maps Medium
Кстати, мы уже приняли доклад Антона в программу AppsConf 2019. Напомню, мы перенесли AppsConf с осени на весну, и следующая самая полезная конференция для мобильных разработчиков пройдет 22 и 23 апреля. Пора-пора задуматься о теме для выступления и подать доклад, или обсудить с руководителем важность походов на конференцию и забронировать билет.
