AA-Tree or Simple Binary Tree
The topic of binary trees has already been discussed on the hub ( here and here ).
About the AA-tree, it was said that "due to the additional restriction, operations are easier than red-black trees (by reducing the number of cases to be analyzed)."
However, it seems to me that the AA tree deserves a separate article.
Why?
Because in fact this is the fastest (or one of the fastest) binary tree with a simple implementation.
I will leave it outside the scope of this article to consider insertion and deletion algorithms in AVL and red-black tree, but their implementation, as a rule, is not trivial. Why?
As you know, the main problem of a binary tree is its balancing, that is, counteraction to degeneration into a regular linked list. Usually, when balancing a tree, there are many options for the mutual arrangement of vertices, each of which must be taken into account separately in the algorithm.
AA-tree was invented by Arne Andersson, who decided that to facilitate balancing the tree need to introduce the concept of the level ( level ) peak. If you imagine a tree growing from top to bottom from the root (that is, “standing on the leaves”), then the level of any leaf vertex will be 1. In his work, Arne Andersson gives a simple rule that an AA tree must satisfy:
You can attach another vertex to one vertex topthe same level but only one and only on the right .
(In his article, the author of the AA-tree uses a slightly different terminology related to 2-3 trees, but the essence does not change).
Thus, the introduced concept of the peak level does not always coincide with the real peak height (distance from the ground), but the tree maintains balance when following the rule “one right connection at one level”.
To balance the AA tree, you need only 2 ( two ) operations.
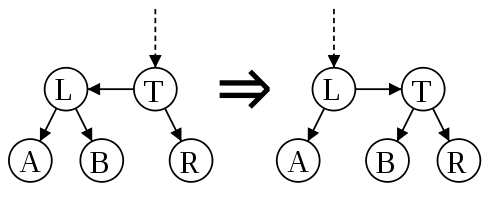
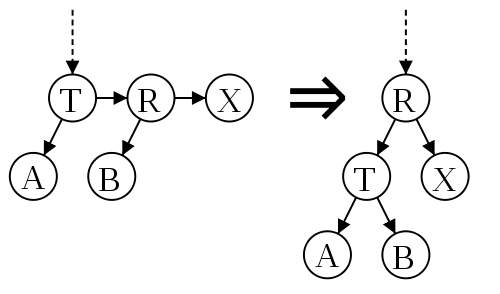
It is easy to understand them from the rule “one right single-level connection”: this is the elimination of the left connection at the same level and the elimination of two right connections at the same level.
These operations are named in the original work of skew and split , respectively. In the above figures, the horizontal arrow denotes the relationship between the vertices of one level, and the inclined (vertical) - between the vertices of different levels.
skew, eliminating the left link at the same level
split, eliminating the two right links at the same level
Let's see what the insert and delete look like in the AA tree. To simplify the implementation, we introduce the concept of the bottom bottom (" ground "). Her level is always 0 and her left and right connections point to her. All leaf vertices refer to bottom instead of storing 0 in the link.
Within the weeks of Delphi on Habré, the source code will be in the form of a pseudo-code similar to Delphi (forcoffee lovers C ++: the operation P ^ .x in Delphi is equivalent to P-> x , var means that the variable is passed by reference, and not by value, i.e., when changing, the external variable changes).
Define the top of the AA-tree.
Inserting a newkey element is easiest to look for in a recursive implementation.
To insert the newkey key into the tree, call NodeInsert (root, newkey) . We get down from the root down the tree, comparing the keys; insert; go up and perform balancing: skew and split for each vertex.
Removing is a little trickier.
Two auxiliary variables are used - deleted and last. When descending down the tree (as during insertion), the vertex keys are compared with the deleted key. If the vertex key is less than the deleted one, then go to the left link, otherwise - to the right (i.e., go to the right even if the keys match). In last, each traversed vertex is entered, and in deleted - only the one where "turned right."
When the bottom of the tree is reached, deleted points to the top where the key to be deleted is located (if it is in the tree), and last points to the top that should be deleted (it can be the same vertex). The key is transferred from last to deleted and the last vertex is deleted.
Next, balancing is performed - you need to perform 3 skew and 2 split.
The implementation of skew and split is commonplace.
In fact, the given pseudo-code is sufficient to create an AA-tree implementation (add only "little things" like modifying the root of a tree (root), etc.).
Some useful links.
Implementation of an AA-tree in C.
A wonderful applet in which you can play with various types of trees (including AA-trees).
Delphi project with AA tree visualization and source code. Wikipedia
article .
About the AA-tree, it was said that "due to the additional restriction, operations are easier than red-black trees (by reducing the number of cases to be analyzed)."
However, it seems to me that the AA tree deserves a separate article.
Why?
Because in fact this is the fastest (or one of the fastest) binary tree with a simple implementation.
I will leave it outside the scope of this article to consider insertion and deletion algorithms in AVL and red-black tree, but their implementation, as a rule, is not trivial. Why?
As you know, the main problem of a binary tree is its balancing, that is, counteraction to degeneration into a regular linked list. Usually, when balancing a tree, there are many options for the mutual arrangement of vertices, each of which must be taken into account separately in the algorithm.
AA-tree was invented by Arne Andersson, who decided that to facilitate balancing the tree need to introduce the concept of the level ( level ) peak. If you imagine a tree growing from top to bottom from the root (that is, “standing on the leaves”), then the level of any leaf vertex will be 1. In his work, Arne Andersson gives a simple rule that an AA tree must satisfy:
You can attach another vertex to one vertex topthe same level but only one and only on the right .
(In his article, the author of the AA-tree uses a slightly different terminology related to 2-3 trees, but the essence does not change).
Thus, the introduced concept of the peak level does not always coincide with the real peak height (distance from the ground), but the tree maintains balance when following the rule “one right connection at one level”.
To balance the AA tree, you need only 2 ( two ) operations.
It is easy to understand them from the rule “one right single-level connection”: this is the elimination of the left connection at the same level and the elimination of two right connections at the same level.
These operations are named in the original work of skew and split , respectively. In the above figures, the horizontal arrow denotes the relationship between the vertices of one level, and the inclined (vertical) - between the vertices of different levels.
skew, eliminating the left link at the same level

split, eliminating the two right links at the same level

Let's see what the insert and delete look like in the AA tree. To simplify the implementation, we introduce the concept of the bottom bottom (" ground "). Her level is always 0 and her left and right connections point to her. All leaf vertices refer to bottom instead of storing 0 in the link.
Within the weeks of Delphi on Habré, the source code will be in the form of a pseudo-code similar to Delphi (for
Define the top of the AA-tree.
PNode = ^ TNode;
TNode = packed record
left, right: PNode;
level: integer; // level; 1 on the leaves
key: pointer; // key, data associated with the vertex
end;
Inserting a newkey element is easiest to look for in a recursive implementation.
procedure NodeInsert (var P: PNode; newkey: pointer);
begin
if P = bottom then begin // reached the bottom - create a new vertex
new (P);
P ^ .left: = bottom;
P ^ .right: = bottom;
P ^ .level: = 1;
P ^ .key: = newkey;
end else begin
if newkey <P ^ .key then
NodeInsert (P ^ .left, newkey)
else if newkey> P ^ .key then
NodeInsert (P ^ .right, newkey)
else begin
P ^ .key: = newkey;
exit
end;
Skew (P);
Split (P);
end;
end;
To insert the newkey key into the tree, call NodeInsert (root, newkey) . We get down from the root down the tree, comparing the keys; insert; go up and perform balancing: skew and split for each vertex.
Removing is a little trickier.
procedure NodeDelete (var P: PNode; newkey: pointer);
begin
if P <> bottom then begin
// 1. go down and remember last and deleted
last: = P;
if Compare (newkey, P) <0 then // newkey <key
NodeDelete (P ^ .left, newkey)
else begin
deleted: = P;
NodeDelete (P ^ .right, newkey);
end;
// 2. delete the element if found
if (P = last) and (deleted <> bottom) and (newkey == deleted ^ .key) then begin
deleted ^ .key: = P ^ .key;
deleted: = bottom;
P: = P ^ .right;
delete last;
end else if (P ^ .left.level <P ^ .level - 1) or (P ^ .right.level <P ^ .level - 1) then begin
// 3. perform balancing while moving up
Dec (P ^ .level);
if P ^ .right.level> P ^ .level then P ^ .right.level: = P ^ .level;
Skew (P);
Skew (P ^ .right);
Skew (P ^ .right ^ .right);
Split (P);
Split (P ^ .right);
end;
end;
end;
Two auxiliary variables are used - deleted and last. When descending down the tree (as during insertion), the vertex keys are compared with the deleted key. If the vertex key is less than the deleted one, then go to the left link, otherwise - to the right (i.e., go to the right even if the keys match). In last, each traversed vertex is entered, and in deleted - only the one where "turned right."
When the bottom of the tree is reached, deleted points to the top where the key to be deleted is located (if it is in the tree), and last points to the top that should be deleted (it can be the same vertex). The key is transferred from last to deleted and the last vertex is deleted.
Next, balancing is performed - you need to perform 3 skew and 2 split.
The implementation of skew and split is commonplace.
// swap the _content_ of records with vertices (not pointers)
procedure Swap (P1, P2: PNode);
var
tmp: TNode;
begin
tmp: = P1 ^;
P1 ^: = P2 ^;
P2 ^: = tmp;
end;
procedure Skew (T: PNode);
var
L: PNode;
begin
L: = T ^ .left;
if T ^ .level = L ^ .level then begin
Swap (T, L); // now T ==> L, L ==> T
L ^ .left: = T ^ .right; // i.e. T.left = L.right
T ^ .right: = L; // i.e. L.right = T
end;
end;
procedure Split (T: PNode);
var
R: PNode;
begin
R: = T ^ .right;
if T ^ .level = R ^ .right ^ .level then begin
Swap (T, R); // now T ==> R, R ==> T
R ^ .right: = T ^ .left;
T ^ .left: = R;
Inc (T ^ .level);
end;
end;
In fact, the given pseudo-code is sufficient to create an AA-tree implementation (add only "little things" like modifying the root of a tree (root), etc.).
Some useful links.
Implementation of an AA-tree in C.
A wonderful applet in which you can play with various types of trees (including AA-trees).
Delphi project with AA tree visualization and source code. Wikipedia
article .
