Heuristic investment portfolio formation algorithms
Suppose we have $ 100 million to invest in several possible investments. Each of these investments has a different value and a different expected return. We must decide how to spend money to get the maximum profit.
Tasks of this type are called portfolio building tasks. We have several positions (investments) that should fit in a fixed-size portfolio ($ 100 million). Each position has its own profitability. You need to find a set of positions that are placed in the portfolio and give maximum profit.
Many of you will say that no heuristics are needed here, and that it is quite possible to get by with exhaustive search. Others will say that a complete search is not needed, because there is a method of branches and borders. But what if the number of possible investments is 65? The complete decision tree contains more than 7 * 10 ^ 19 nodes. Suppose the branch and bound method iterates over a tenth of a percent of these nodes, and the computer checks a million nodes per second. Under these conditions, it would take more than 2 million years to solve the problem. It is for such complex tasks that heuristics are used. If you are interested, you are welcome to cat.
The heuristic method of climbing a hill makes changes to the current solution, moving it as close to the target as possible. This process is called hill climbing, because it looks like a lost traveler trying to reach the top of the mountain at night. Even if it is already too dark to see something in the distance, he can try to reach the top of the mountain, constantly moving up.
Of course, there is a chance that the traveler will stop at the top of a smaller hill and not reach a peak. This problem exists when using this heuristic method. The algorithm may find a solution that is locally optimal, but not the best possible solution.
In the task of forming an investment portfolio, the goal is to choose a set of positions with a total value of no more than the allowable limit, and the total profit should be as large as possible. Hill climbing heuristics for this task selects a position that gives maximum profit at every step. At the same time, the decision will better meet the goal of maximizing profit.
The algorithm first adds the position with the maximum profit to the solution, then the next position with the maximum profit is added (provided that the full price remains within the acceptable limits). Joining positions with maximum profit will continue until the limit of value has been exhausted.
For the list of investments below, the program will first select deal A because it has the largest return ($ 9 million). Then transaction C is selected because it has the largest profit remaining ($ 8 million). At this point in time, out of the allowable 100 million, 93 million has already been spent, and the algorithm will no longer be able to select any transactions. The solution calculated using this heuristic includes elements A and C, costs 93 million and makes a profit of 17 million.

Climbing heuristics fill a portfolio very quickly. If the elements are initially ordered in the order of decreasing profit, then the complexity of the algorithm is about O (N). The program simply moves around the list, adding positions with maximum profit, until the limit of funds is exhausted. If the list is not sorted, then the complexity of this algorithm is N * log (N). This is much better than the O (2 ^ N) steps needed to completely enumerate all the nodes of a tree. For 20 positions, this heuristic uses about 400 steps, the method of branches and borders - several thousand, and exhaustive search - more than 2 million.
The strategy, which in some ways is the opposite of the hill climbing method, is called the least cost method. Instead of bringing the solution as close to the goal as possible at each step, you can try to reduce the cost of the solution. In the example with the formation of an investment portfolio at each step, a position with a minimum cost is added to the solution.
This strategy will place as many positions as possible in the solution. This works well if all positions have approximately the same value. But if an expensive transaction brings big profits, this strategy may miss the chance, giving not the best possible result.
For the investments mentioned above, the minimum cost strategy begins by first adding transaction E worth 23 million to the solution. Then it selects position D worth 27 million and C worth 30 million. At this point, the algorithm has already spent 80 million out of 100 million dollars and can no longer make a single investment.
The resulting solution costs 80 million and makes a profit of 18 million. This is a million better than the solution that the heuristic for climbing the hill gives us, but the minimum cost algorithm does not always work more efficiently than the algorithm for climbing the hill. Which method will give the best solution depends on the specific data.
The structure of programs that implement heuristics of minimum cost and heuristics of climbing the hill is almost identical. The only difference is the choice of the next position, which is added to the existing solution. The minimum cost method instead of the position with the maximum profit selects the position that has the lowest cost. Since the two methods are very similar, their complexity is the same. If the positions are properly sorted, both algorithms have complexity of the order of O (N). With a random arrangement of positions, their complexity will be of the order of O (N * log (N)).
The hill climbing strategy does not take into account the value of added positions. She selects positions with maximum profit, even if they are of great value. The minimum cost strategy does not take into account the profit brought by the position. She selects items at low cost, even if they have little profit.
Balanced profit heuristics compares both profit and position value to determine which positions need to be selected. At each step, the heuristic selects the element with the highest ratio of profit to value (provided that after the investment is included in the portfolio, the total price will remain within acceptable limits).
We include in the table a new column - the ratio of profit / value. With this approach, position C is first selected because it has the highest ratio of 0.27. Then D is added with a ratio of 0.26 and B with a ratio of 0.20. At this point, 92 million out of 100 million was spent, and not a single position can be added to the solution.
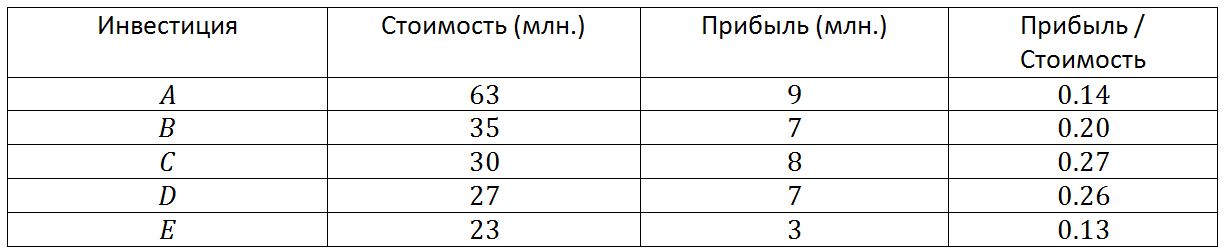
This solution has a value of 92 million and gives a profit of 22 million. This is 4 million better than the solution found using the minimum cost method and 5 million better than the solution found by the heuristic hill climbing. Moreover, the solution found will generally be the best of all possible, which will be confirmed by search by exhaustive search or by the method of branches and boundaries. But it’s important to understand that balanced profit is still a heuristic, therefore, with the help of this, the best possible solution is not always found. Very often, this method finds better solutions than solutions found by methods of climbing a hill and at a minimum cost, but this does not always happen. The structure of the program that implements the heuristic of balanced profit is almost identical to the structure of hill climbing programs and the minimum cost. The only difference is the way you select the next position that is added to the solution. The complexity of this heuristic is proportional to O (N), subject to preliminary sorting. If the positions are located arbitrarily, the complexity of the algorithm will be O (N * log (N)).
A random search is performed according to its name. At each step, the algorithm adds a randomly selected position that satisfies the boundaries of the cost. This type of enumeration is called the Monte Carlo method.
Since a randomly selected solution is unlikely to be the best, to obtain an acceptable result, you must repeat the search several times. Although at first glance it seems that the probability of finding a good solution is very small, the use of this method sometimes produces surprisingly good results. Depending on the initial data and the number of random solutions checked, this heuristic often works better than hill climbing methods and minimal cost.
The advantage of random search is that this method is easy to understand and implement. Sometimes it’s hard to imagine how to implement a method of climbing a hill, minimum cost or reduced profit for a specific task, but it is always easy to generate solutions at random. Even to solve extremely complex problems, random search is the simplest method.
Another strategy is to start with a random solution and then make a consistent approximation. Starting with a randomly generated solution, the program makes a random choice. If the new solution is an improvement on the previous one, the program consolidates the change and continues to check other items. If the change does not improve the solution, the program refuses it and makes a new attempt.
It is especially simple to implement the method of consistent approximation for the task of forming a portfolio of investments. The program merely selects a random position from the trial solution and removes it from the current one. Then she randomly adds positions to the decision until the limit of funds is exhausted. If the deleted position had a very high cost, then the program can add several positions not its place.
Like random search, this heuristic is easy to understand and implement. To solve a complex problem, it is not easy to create algorithms for climbing a hill, minimum cost and reduced profit, but it is quite simple to write a heuristic algorithm for successive approximation.
There are several good ways to determine when to stop random changes. For example, a fixed number of changes are allowed. For a task of N elements, you can make N or N ^ 2 random changes and then stop the program.
Another strategy is to make changes until successive changes bring improvement. As soon as several consecutive changes do not give improvements, the program can be stopped.
If the program replaces a randomly selected position in the trial solution, it may find a solution that can no longer be improved, but it still will not be the best possible solution. As an example, consider the following set of possible investments. Suppose the algorithm randomly selects positions A and B as the initial solution. Its value will be equal to 90 million, it will bring a profit of 17 million. If the program removes either A or B, then the solution will have a fairly high cost, so the program can add only one new position. Since positions A and B have the largest profits, replacing them with another position will reduce the total profit. Accidentally deleting one position from this solution will never lead to improvement.

The best solution contains positions C, D, E. Its total cost is 98 million, total profit is 18 million. To find this solution, the algorithm must remove both positions A and B from the solution at once and add new ones in their place.
Such decisions, when small changes cannot improve the solutions, are called the local optimum. There are two ways in which the program will not stop at a local optimum, but will look for a global optimum.
First, the program can be changed so that it removes several items from the solution. If the program deletes two randomly selected items, it can find the right solution for this example. However, for larger tasks, deleting two positions is usually not enough. The program will need to delete three, four, or maybe more positions.
A simpler way is to perform more tests with different initial solutions. Some of the initial solutions can lead to local optima, but one of them will achieve a global optimum.
The annealing method is borrowed from thermodynamics. During annealing, the metal is heated to a high temperature. The molecules in the hot metal make rapid vibrations. If the metal is slowly cooled, then the molecules begin to line up, forming crystals. In this case, the molecules gradually turn into a state with minimal energy.
When the metal cools, neighboring crystals merge with each other. Molecules of one crystal temporarily leave their positions with minimal energy and combine with molecules of another crystal. The energy of the resulting larger crystal will be less than the sum of the energies of the two original crystals. If the metal is cooled sufficiently slowly, the crystals will become simply huge. The final arrangement of the molecules will have a very low total energy, so the metal will be very strong.
Starting from a high energy state, molecules ultimately reach a low energy state. On their way to their final position, they go through many local energy minima. Each crystal combination represents a local minimum. The crystal can be brought to the minimum energy state only by temporal resolution of the structure of smaller crystals, thereby increasing the energy of the system, as a result of which the crystals can combine.
The annealing method uses a similar method for finding the best solution to a problem. When a program searches for a solution, it may be stuck in a local optimum. To avoid this, she occasionally makes random changes to the solution, even if the next option does not immediately improve the result. This allows the program to exit the local optimum and find the best solution.
To prevent the program from focusing on these modifications, the algorithm after a while changes the probability of making random changes. The probability of making one change is P = 1 / e ^ (E / (k * T)), where E is the amount of “energy” added to the system, k is a constant selected depending on the kind of problem, and T is a variable corresponding to “temperature ".
First, the value of T should be quite high, so the likelihood of changes will also be quite high. After some time, the value of T decreases, and the probability of random changes also decreases. Once the process has reached a point at which no changes can improve the solution and the value of T becomes so small that random changes are very rare, the algorithm will finish the job.
For the task of forming a portfolio of investments, E is the value by which profit is reduced as a result of the change. For example, if we delete a position with a profit of $ 10 million and replace it with a position with a profit of $ 7 million, the energy added to the system will be equal to 3. If the value of E is large, then the probability of changes is small, therefore, the probability of large changes below.
Different heuristic methods behave differently in different tasks. To solve the problem of forming a portfolio of investments, the heuristic of balanced profit is good enough, given its simplicity. The sequential approach strategy also works quite well, but requires much more time. For other tasks, some other heuristic may be best, including one not considered in this chapter.
Heuristics work much faster than brute force and branch and bound methods. Some heuristic approaches (climbing a hill, minimum cost, balanced profit, etc.) work extremely fast because they consider only one possible solution. These methods work so fast that sometimes it makes sense to execute them all in turn, and then choose the best of the three solutions obtained. Of course, it is impossible to guarantee that this solution will be the best, but it will certainly be good enough.
Tasks of this type are called portfolio building tasks. We have several positions (investments) that should fit in a fixed-size portfolio ($ 100 million). Each position has its own profitability. You need to find a set of positions that are placed in the portfolio and give maximum profit.
Many of you will say that no heuristics are needed here, and that it is quite possible to get by with exhaustive search. Others will say that a complete search is not needed, because there is a method of branches and borders. But what if the number of possible investments is 65? The complete decision tree contains more than 7 * 10 ^ 19 nodes. Suppose the branch and bound method iterates over a tenth of a percent of these nodes, and the computer checks a million nodes per second. Under these conditions, it would take more than 2 million years to solve the problem. It is for such complex tasks that heuristics are used. If you are interested, you are welcome to cat.
Climbing the hill
The heuristic method of climbing a hill makes changes to the current solution, moving it as close to the target as possible. This process is called hill climbing, because it looks like a lost traveler trying to reach the top of the mountain at night. Even if it is already too dark to see something in the distance, he can try to reach the top of the mountain, constantly moving up.
Of course, there is a chance that the traveler will stop at the top of a smaller hill and not reach a peak. This problem exists when using this heuristic method. The algorithm may find a solution that is locally optimal, but not the best possible solution.
In the task of forming an investment portfolio, the goal is to choose a set of positions with a total value of no more than the allowable limit, and the total profit should be as large as possible. Hill climbing heuristics for this task selects a position that gives maximum profit at every step. At the same time, the decision will better meet the goal of maximizing profit.
The algorithm first adds the position with the maximum profit to the solution, then the next position with the maximum profit is added (provided that the full price remains within the acceptable limits). Joining positions with maximum profit will continue until the limit of value has been exhausted.
For the list of investments below, the program will first select deal A because it has the largest return ($ 9 million). Then transaction C is selected because it has the largest profit remaining ($ 8 million). At this point in time, out of the allowable 100 million, 93 million has already been spent, and the algorithm will no longer be able to select any transactions. The solution calculated using this heuristic includes elements A and C, costs 93 million and makes a profit of 17 million.

Climbing heuristics fill a portfolio very quickly. If the elements are initially ordered in the order of decreasing profit, then the complexity of the algorithm is about O (N). The program simply moves around the list, adding positions with maximum profit, until the limit of funds is exhausted. If the list is not sorted, then the complexity of this algorithm is N * log (N). This is much better than the O (2 ^ N) steps needed to completely enumerate all the nodes of a tree. For 20 positions, this heuristic uses about 400 steps, the method of branches and borders - several thousand, and exhaustive search - more than 2 million.
Least Cost Method
The strategy, which in some ways is the opposite of the hill climbing method, is called the least cost method. Instead of bringing the solution as close to the goal as possible at each step, you can try to reduce the cost of the solution. In the example with the formation of an investment portfolio at each step, a position with a minimum cost is added to the solution.
This strategy will place as many positions as possible in the solution. This works well if all positions have approximately the same value. But if an expensive transaction brings big profits, this strategy may miss the chance, giving not the best possible result.
For the investments mentioned above, the minimum cost strategy begins by first adding transaction E worth 23 million to the solution. Then it selects position D worth 27 million and C worth 30 million. At this point, the algorithm has already spent 80 million out of 100 million dollars and can no longer make a single investment.
The resulting solution costs 80 million and makes a profit of 18 million. This is a million better than the solution that the heuristic for climbing the hill gives us, but the minimum cost algorithm does not always work more efficiently than the algorithm for climbing the hill. Which method will give the best solution depends on the specific data.
The structure of programs that implement heuristics of minimum cost and heuristics of climbing the hill is almost identical. The only difference is the choice of the next position, which is added to the existing solution. The minimum cost method instead of the position with the maximum profit selects the position that has the lowest cost. Since the two methods are very similar, their complexity is the same. If the positions are properly sorted, both algorithms have complexity of the order of O (N). With a random arrangement of positions, their complexity will be of the order of O (N * log (N)).
Balanced profit
The hill climbing strategy does not take into account the value of added positions. She selects positions with maximum profit, even if they are of great value. The minimum cost strategy does not take into account the profit brought by the position. She selects items at low cost, even if they have little profit.
Balanced profit heuristics compares both profit and position value to determine which positions need to be selected. At each step, the heuristic selects the element with the highest ratio of profit to value (provided that after the investment is included in the portfolio, the total price will remain within acceptable limits).
We include in the table a new column - the ratio of profit / value. With this approach, position C is first selected because it has the highest ratio of 0.27. Then D is added with a ratio of 0.26 and B with a ratio of 0.20. At this point, 92 million out of 100 million was spent, and not a single position can be added to the solution.

This solution has a value of 92 million and gives a profit of 22 million. This is 4 million better than the solution found using the minimum cost method and 5 million better than the solution found by the heuristic hill climbing. Moreover, the solution found will generally be the best of all possible, which will be confirmed by search by exhaustive search or by the method of branches and boundaries. But it’s important to understand that balanced profit is still a heuristic, therefore, with the help of this, the best possible solution is not always found. Very often, this method finds better solutions than solutions found by methods of climbing a hill and at a minimum cost, but this does not always happen. The structure of the program that implements the heuristic of balanced profit is almost identical to the structure of hill climbing programs and the minimum cost. The only difference is the way you select the next position that is added to the solution. The complexity of this heuristic is proportional to O (N), subject to preliminary sorting. If the positions are located arbitrarily, the complexity of the algorithm will be O (N * log (N)).
Random methods
Random search
A random search is performed according to its name. At each step, the algorithm adds a randomly selected position that satisfies the boundaries of the cost. This type of enumeration is called the Monte Carlo method.
Since a randomly selected solution is unlikely to be the best, to obtain an acceptable result, you must repeat the search several times. Although at first glance it seems that the probability of finding a good solution is very small, the use of this method sometimes produces surprisingly good results. Depending on the initial data and the number of random solutions checked, this heuristic often works better than hill climbing methods and minimal cost.
The advantage of random search is that this method is easy to understand and implement. Sometimes it’s hard to imagine how to implement a method of climbing a hill, minimum cost or reduced profit for a specific task, but it is always easy to generate solutions at random. Even to solve extremely complex problems, random search is the simplest method.
Sequential approach
Another strategy is to start with a random solution and then make a consistent approximation. Starting with a randomly generated solution, the program makes a random choice. If the new solution is an improvement on the previous one, the program consolidates the change and continues to check other items. If the change does not improve the solution, the program refuses it and makes a new attempt.
It is especially simple to implement the method of consistent approximation for the task of forming a portfolio of investments. The program merely selects a random position from the trial solution and removes it from the current one. Then she randomly adds positions to the decision until the limit of funds is exhausted. If the deleted position had a very high cost, then the program can add several positions not its place.
Like random search, this heuristic is easy to understand and implement. To solve a complex problem, it is not easy to create algorithms for climbing a hill, minimum cost and reduced profit, but it is quite simple to write a heuristic algorithm for successive approximation.
Stop moment
There are several good ways to determine when to stop random changes. For example, a fixed number of changes are allowed. For a task of N elements, you can make N or N ^ 2 random changes and then stop the program.
Another strategy is to make changes until successive changes bring improvement. As soon as several consecutive changes do not give improvements, the program can be stopped.
Local optimum
If the program replaces a randomly selected position in the trial solution, it may find a solution that can no longer be improved, but it still will not be the best possible solution. As an example, consider the following set of possible investments. Suppose the algorithm randomly selects positions A and B as the initial solution. Its value will be equal to 90 million, it will bring a profit of 17 million. If the program removes either A or B, then the solution will have a fairly high cost, so the program can add only one new position. Since positions A and B have the largest profits, replacing them with another position will reduce the total profit. Accidentally deleting one position from this solution will never lead to improvement.

The best solution contains positions C, D, E. Its total cost is 98 million, total profit is 18 million. To find this solution, the algorithm must remove both positions A and B from the solution at once and add new ones in their place.
Such decisions, when small changes cannot improve the solutions, are called the local optimum. There are two ways in which the program will not stop at a local optimum, but will look for a global optimum.
First, the program can be changed so that it removes several items from the solution. If the program deletes two randomly selected items, it can find the right solution for this example. However, for larger tasks, deleting two positions is usually not enough. The program will need to delete three, four, or maybe more positions.
A simpler way is to perform more tests with different initial solutions. Some of the initial solutions can lead to local optima, but one of them will achieve a global optimum.
Annealing method
The annealing method is borrowed from thermodynamics. During annealing, the metal is heated to a high temperature. The molecules in the hot metal make rapid vibrations. If the metal is slowly cooled, then the molecules begin to line up, forming crystals. In this case, the molecules gradually turn into a state with minimal energy.
When the metal cools, neighboring crystals merge with each other. Molecules of one crystal temporarily leave their positions with minimal energy and combine with molecules of another crystal. The energy of the resulting larger crystal will be less than the sum of the energies of the two original crystals. If the metal is cooled sufficiently slowly, the crystals will become simply huge. The final arrangement of the molecules will have a very low total energy, so the metal will be very strong.
Starting from a high energy state, molecules ultimately reach a low energy state. On their way to their final position, they go through many local energy minima. Each crystal combination represents a local minimum. The crystal can be brought to the minimum energy state only by temporal resolution of the structure of smaller crystals, thereby increasing the energy of the system, as a result of which the crystals can combine.
The annealing method uses a similar method for finding the best solution to a problem. When a program searches for a solution, it may be stuck in a local optimum. To avoid this, she occasionally makes random changes to the solution, even if the next option does not immediately improve the result. This allows the program to exit the local optimum and find the best solution.
To prevent the program from focusing on these modifications, the algorithm after a while changes the probability of making random changes. The probability of making one change is P = 1 / e ^ (E / (k * T)), where E is the amount of “energy” added to the system, k is a constant selected depending on the kind of problem, and T is a variable corresponding to “temperature ".
First, the value of T should be quite high, so the likelihood of changes will also be quite high. After some time, the value of T decreases, and the probability of random changes also decreases. Once the process has reached a point at which no changes can improve the solution and the value of T becomes so small that random changes are very rare, the algorithm will finish the job.
For the task of forming a portfolio of investments, E is the value by which profit is reduced as a result of the change. For example, if we delete a position with a profit of $ 10 million and replace it with a position with a profit of $ 7 million, the energy added to the system will be equal to 3. If the value of E is large, then the probability of changes is small, therefore, the probability of large changes below.
Comparison of heuristic methods
Different heuristic methods behave differently in different tasks. To solve the problem of forming a portfolio of investments, the heuristic of balanced profit is good enough, given its simplicity. The sequential approach strategy also works quite well, but requires much more time. For other tasks, some other heuristic may be best, including one not considered in this chapter.
Heuristics work much faster than brute force and branch and bound methods. Some heuristic approaches (climbing a hill, minimum cost, balanced profit, etc.) work extremely fast because they consider only one possible solution. These methods work so fast that sometimes it makes sense to execute them all in turn, and then choose the best of the three solutions obtained. Of course, it is impossible to guarantee that this solution will be the best, but it will certainly be good enough.
