Index Types Overview Oracle, MySQL, PostgreSQL, MS SQL
In one of the comments there was a request to tell you more about indexes, and since there are practically no summary data on supported indexes of various DBMSs in Runet, in this review I will consider what types of indexes are supported in the most popular DBMSs
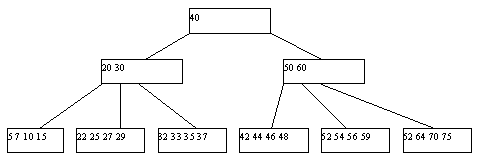
The B-Tree index family is the most commonly used type of index, organized as a balanced tree of ordered keys. They are supported by almost all DBMSs, both relational and non-relational, and for almost all data types. Since most probably know them well (or can read about them here , for example ), the only thing that should be noted here is that this type of index is optimal for a set with a good distribution of values and high power (cardinality -number of unique values).
At the moment, all DBMS data has spatial data types and functions for working with them; for Oracle, it is a set of types and functions in the MDSYS scheme; for PostgreSQL, it is point, line, lseg, polygon, box, path, polygon, circle, in MySQL - geometry, point, linestring, polygon, multipoint, multilinestring, multipolygon, geometrycollection, MS SQL - Point, MultiPoint, LineString, MultiLineString, Polygon, MultiPolygon, GeometryCollection.
In the spatial query operation scheme, two stages or two stages of filtering are usually distinguished. DBMSs with poor spatial support work out only the first stage (coarse filtering, MySQL). As a rule, an approximate, approximated representation of objects is used at this stage. The most common type of approximation is the Minimum Bounding Rectangle [MBR] [100].
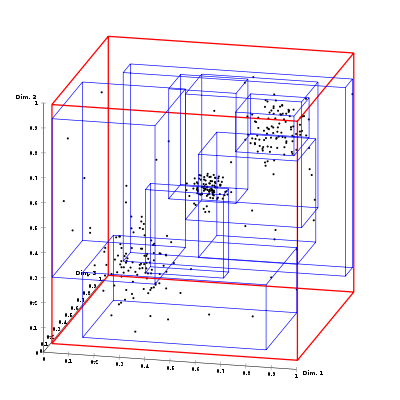
For spatial data types, there are special indexing methods based on R-trees (R-Tree index) and grids (Grid-based Spatial index).
Spatial grid index is a tree structure similar to a B-tree, but is used to organize access to Spatial data, that is, to index multidimensional information, such as, for example, geographic data with two-dimensional coordinates (latitude and longitude) ) In this structure, the nodes of the tree are the cells of space. For example, for two-dimensional space: first, the entire parent area will be divided into a strictly defined resolution grid, then each grid cell in which the number of objects exceeds the set maximum of objects in the cell will be divided into the next level subgrid. This process will continue until maximum nesting is achieved (if installed), or until everything is divided up to cells not exceeding the maximum of objects.

In the case of three-dimensional or multidimensional space, these will be rectangular parallelepipeds (cuboids) or parallelepots.
Quadtree is a subset of the Grid-based Spatial index, in which there are always 4 children in the parent cell and the grid resolution varies depending on the nature or complexity of the data.

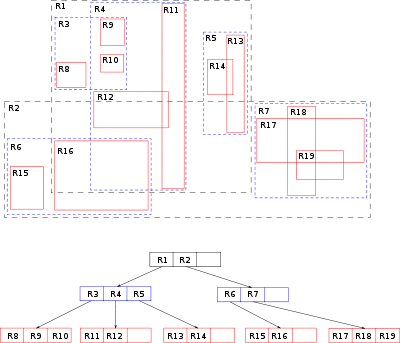
R-Tree (Regions Tree) is also a tree-like data structure similar to the Spatial Grid, proposed in 1984 by Antonin Guttman. This data structure also splits the space into many hierarchically nested cells, but which, unlike the Spatial Grid, are not required to completely cover the parent cell and can intersect.
Various algorithms can be used to split overflowed vertices, which causes the division of R-trees into subtypes: with quadratic and linear complexity (Guttman, of course, described with exponential complexity - Exhaustive Search, but he, of course, is not used anywhere).
The quadratic subtype is divided into two rectangles with a minimum area covering all objects. Linear - divided by maximum distance.
Hash indexes were proposed by Arthur Fuller, and they do not store the values themselves, but their hashes, which reduces the size (and, accordingly, increases the processing speed) of indexes from large fields. Thus, when querying using HASH indexes, not the one searched for from the field value will be compared, but the hash from the sought value with the field hashes.
Due to the nonlinear nature of the hash functions, this index cannot be sorted by value, which makes it impossible to use more / less and “is null” comparisons. In addition, since hashes are not unique, collision resolution methods are used for matching hashes.
Bitmap index - the method of bit indexes is to create separate bitmaps (a sequence of 0 and 1) for each possible column value, where each bit corresponds to a row with an indexed value, and its value equal to 1 means that the record corresponding to the bit position contains an indexed value for this column or property.
Bitmaps
The main advantage of bit indexes is that on large sets with low power and good clustering by their values, the index will be less than B * -tree. (Read more here or here )
Reverse index is also a B-tree index but with a reversed key, used mainly for monotonically increasing values (for example, auto-incrementing identifier) in OLTP systems in order to remove competition for the last leaf block of the index, because by flipping the value, two adjacent index entries fall into different index blocks. It cannot be used for range searching.
Example:
As you can see, the value in the index changes much more than the value in the table itself, and therefore in the b-tree structure, they will fall into different blocks.
An inverted index is a full-text index that stores for each key token a sorted list of addresses of table entries that contain a given key.
In a simplified form, it will look like this:
Partial index is an index built on the part of a table that satisfies a certain condition of the index itself. This index was created to reduce the size of the index.
The most flexible type of indexes are functional indexes, that is, indexes whose keys store the result of user-defined functions. Functional indexes are often built for fields whose values are pre-processed before comparison in the SQL command. For example, when comparing string data without case sensitivity, the UPPER function is often used. Creating a functional index with the UPPER function improves the effectiveness of such comparisons.
In addition, a functional index can help to implement any other missing type of indexes for a given DBMS (except, perhaps, a bit index, for example, Hash for Oracle)
It is worth mentioning that in PostgreSQL GiST allows you to create an index based on R-Tree for any native data type. To do this, you need to implement all 7 functions of the R-Tree mechanism.
You can read more here:
Oracle Spatial User's Guide and Reference
Spatial data in MS SQL
MS SQL: Spatial Indexing Overview
Hilbert R-tree
Spatial types PostgreSQL
Spatial functions PostgreSQL
Indexing spatial data in DBMS Microsoft SQL Server 2000
Papadias D., Theodoridis T. Spatial Relations , Minimum Bounding Rectangles and Spatial Data Structures // Technical Report KDB-SLAB-TR-94-04,
Faloutsos C., Kamel I. Hilbert R-Tree: An Improved R-Tree UsingFractals // Department of CS, University of Maryland, TechnicalResearch Report TR-93-19,
Wikipedia: Hilbert R-tree
External Search Methods
Arthur Fuller. Intelligent database design using hash keys
PS. Perhaps I forgot to mention something, write to the PM or in the comments - I will add.
B-tree
The B-Tree index family is the most commonly used type of index, organized as a balanced tree of ordered keys. They are supported by almost all DBMSs, both relational and non-relational, and for almost all data types. Since most probably know them well (or can read about them here , for example ), the only thing that should be noted here is that this type of index is optimal for a set with a good distribution of values and high power (cardinality -number of unique values).

Spatial indexes
At the moment, all DBMS data has spatial data types and functions for working with them; for Oracle, it is a set of types and functions in the MDSYS scheme; for PostgreSQL, it is point, line, lseg, polygon, box, path, polygon, circle, in MySQL - geometry, point, linestring, polygon, multipoint, multilinestring, multipolygon, geometrycollection, MS SQL - Point, MultiPoint, LineString, MultiLineString, Polygon, MultiPolygon, GeometryCollection.
In the spatial query operation scheme, two stages or two stages of filtering are usually distinguished. DBMSs with poor spatial support work out only the first stage (coarse filtering, MySQL). As a rule, an approximate, approximated representation of objects is used at this stage. The most common type of approximation is the Minimum Bounding Rectangle [MBR] [100].
For spatial data types, there are special indexing methods based on R-trees (R-Tree index) and grids (Grid-based Spatial index).
Spatial grid
Spatial grid index is a tree structure similar to a B-tree, but is used to organize access to Spatial data, that is, to index multidimensional information, such as, for example, geographic data with two-dimensional coordinates (latitude and longitude) ) In this structure, the nodes of the tree are the cells of space. For example, for two-dimensional space: first, the entire parent area will be divided into a strictly defined resolution grid, then each grid cell in which the number of objects exceeds the set maximum of objects in the cell will be divided into the next level subgrid. This process will continue until maximum nesting is achieved (if installed), or until everything is divided up to cells not exceeding the maximum of objects.

In the case of three-dimensional or multidimensional space, these will be rectangular parallelepipeds (cuboids) or parallelepots.

Quadtree
Quadtree is a subset of the Grid-based Spatial index, in which there are always 4 children in the parent cell and the grid resolution varies depending on the nature or complexity of the data.

R-tree
R-Tree (Regions Tree) is also a tree-like data structure similar to the Spatial Grid, proposed in 1984 by Antonin Guttman. This data structure also splits the space into many hierarchically nested cells, but which, unlike the Spatial Grid, are not required to completely cover the parent cell and can intersect.
Various algorithms can be used to split overflowed vertices, which causes the division of R-trees into subtypes: with quadratic and linear complexity (Guttman, of course, described with exponential complexity - Exhaustive Search, but he, of course, is not used anywhere).
The quadratic subtype is divided into two rectangles with a minimum area covering all objects. Linear - divided by maximum distance.

Hash
Hash indexes were proposed by Arthur Fuller, and they do not store the values themselves, but their hashes, which reduces the size (and, accordingly, increases the processing speed) of indexes from large fields. Thus, when querying using HASH indexes, not the one searched for from the field value will be compared, but the hash from the sought value with the field hashes.
Due to the nonlinear nature of the hash functions, this index cannot be sorted by value, which makes it impossible to use more / less and “is null” comparisons. In addition, since hashes are not unique, collision resolution methods are used for matching hashes.
Bitmap
Bitmap index - the method of bit indexes is to create separate bitmaps (a sequence of 0 and 1) for each possible column value, where each bit corresponds to a row with an indexed value, and its value equal to 1 means that the record corresponding to the bit position contains an indexed value for this column or property.
| EmpID | Floor |
|---|---|
| 1 | Male |
| 2 | Female |
| 3 | Female |
| 4 | Male |
| 5 | Female |
Bitmaps
| Value | Start | the end | Bit mask |
|---|---|---|---|
| Male | First line address | Last line address | 10010 |
| Female | First line address | Last line address | 01101 |
The main advantage of bit indexes is that on large sets with low power and good clustering by their values, the index will be less than B * -tree. (Read more here or here )
Reverse index
Reverse index is also a B-tree index but with a reversed key, used mainly for monotonically increasing values (for example, auto-incrementing identifier) in OLTP systems in order to remove competition for the last leaf block of the index, because by flipping the value, two adjacent index entries fall into different index blocks. It cannot be used for range searching.
Example:
| Field in the table (bin) | Reverse index key (bin) |
|---|---|
| 00000001 | 10,000,000 |
| ... | ... |
| 00001001 | 10010000 |
| 00001010 | 01010000 |
| 00001011 | 11010000 |
Inverted index
An inverted index is a full-text index that stores for each key token a sorted list of addresses of table entries that contain a given key.
| 1 | Mom washed the frame |
| 2 | Dad washed the frame |
| 3 | Dad washed the car |
| 4 | Mom polished the car |
In a simplified form, it will look like this:
| Mother | 1.4 |
| Soaps | 1 |
| Ramu | 1,2 |
| Dad | 2,3 |
| Polished | 4 |
| A car | 3.4 |
Partial index
Partial index is an index built on the part of a table that satisfies a certain condition of the index itself. This index was created to reduce the size of the index.
Function-based index
The most flexible type of indexes are functional indexes, that is, indexes whose keys store the result of user-defined functions. Functional indexes are often built for fields whose values are pre-processed before comparison in the SQL command. For example, when comparing string data without case sensitivity, the UPPER function is often used. Creating a functional index with the UPPER function improves the effectiveness of such comparisons.
In addition, a functional index can help to implement any other missing type of indexes for a given DBMS (except, perhaps, a bit index, for example, Hash for Oracle)
Index Type Summary Table
| MySQL | PostgreSQL | MS SQL | Oracle | |
| B-tree index | there is | there is | there is | there is |
| Supported Spatial Indexes | Quadratic R-Tree | Rtree_GiST (uses linear splitting) | 4-level Grid-based spatial index (separate for geographic and geodetic data) | R-Tree with quadratic partition; Quadtree |
| Hash index | Only in tables like Memory | there is | Not | Not |
| Bitmap index | Not | there is | Not | there is |
| Reverse index | Not | Not | Not | there is |
| Inverted index | there is | there is | there is | there is |
| Partial index | Not | there is | there is | Not |
| Function based index | Not | there is | there is | there is |
It is worth mentioning that in PostgreSQL GiST allows you to create an index based on R-Tree for any native data type. To do this, you need to implement all 7 functions of the R-Tree mechanism.
You can read more here:
Oracle Spatial User's Guide and Reference
Spatial data in MS SQL
MS SQL: Spatial Indexing Overview
Hilbert R-tree
Spatial types PostgreSQL
Spatial functions PostgreSQL
Indexing spatial data in DBMS Microsoft SQL Server 2000
Papadias D., Theodoridis T. Spatial Relations , Minimum Bounding Rectangles and Spatial Data Structures // Technical Report KDB-SLAB-TR-94-04,
Faloutsos C., Kamel I. Hilbert R-Tree: An Improved R-Tree UsingFractals // Department of CS, University of Maryland, TechnicalResearch Report TR-93-19,
Wikipedia: Hilbert R-tree
External Search Methods
Arthur Fuller. Intelligent database design using hash keys
PS. Perhaps I forgot to mention something, write to the PM or in the comments - I will add.
