Neural networks based on homeostatic neurons: self-organization and targeted behavior

Introduction

In this topic, I want to talk about a model of an unusual neural network, in the development of which I was lucky to participate. This model was developed about a year ago (the authorship is written in the last section), however, its research after this stopped due to a complete lack of time (employment in its own projects). Nevertheless, I will describe it here in the hope that some of the thoughts will seem interesting to readers and will sprout possible further research in this direction.

Immediately make a reservation that this model does not pretend in any way to prototype AI. Rather, we wanted to explore the possibility of self-organization and the prospects for the emergence of holistic, purposeful behavior in a dynamic system of “selfish” (homeostatic) neurons.
It seems to me that for a more complete understanding of the logic of the model, it will be useful to read my topic about the Theory of functional systems , but again this is at your discretion.

Go!

Biological basis

This model was built on the basis of the theory of functional systems P.K. Anokhin and the theory of homeostasis.

Homeostasis - self-regulation, the ability of an open system to maintain the constancy of its internal state through coordinated reactions aimed at maintaining dynamic balance. Walter Canon, who originally coined the term, called homeostasis “the wisdom of the body” [1].

The simplest biological motivations arise when the homeostatic balance is disturbed in the neurons of the corresponding physiological zones (violation of the energy reserves, oxygen, or osmotic imbalance). However, there is a universal unit for assessing biological motivation [2]. The existence of this unit is due to the fact that the satisfaction of any motivation causes pleasure and, accordingly, the removal of the imbalance in the homeostatic system, which generates this motivation. Therefore, modeling homeostasis is a direct path to creating an artificial system with some semblance of motivation, i.e. a system with its own goal and ways to achieve it. There are many factors leading to inconsistencies in the homeostasis system, and there is a hierarchy of such factors, in terms of their importance for cell survival. To maintain higher-level factors in a stable range, homeostasis modifies the optimal levels of regulation of lower-level factors. Those. function recovery can occur not through the return of distorted parameters to normal, but in a roundabout way, through changes in the ratio between these parameters. In particular, excessive excitation damages neurons, but there are some factors that restore homeostasis (like cAMP, Interleukin-1, thyrotropin-releasing hormone). Therefore, compensatory homeostasis can, at an intermediate stage, excite neurons on the way to finding a new equilibrium point. In fig. 1. The scheme of a two-level homeostasis in a neuron is shown. Red in the figure conditionally shows damage to a neuron, and green - restoration. Damage is an external factor causing a mismatch. function recovery can occur not through the return of distorted parameters to normal, but in a roundabout way, through changes in the ratio between these parameters. In particular, excessive excitation damages neurons, but there are some factors that restore homeostasis (like cAMP, Interleukin-1, thyrotropin-releasing hormone). Therefore, compensatory homeostasis can, at an intermediate stage, excite neurons on the way to finding a new equilibrium point. In fig. 1. The scheme of a two-level homeostasis in a neuron is shown. Red in the figure conditionally shows damage to a neuron, and green - restoration. Damage is an external factor causing a mismatch. function recovery can occur not through the return of distorted parameters to normal, but in a roundabout way, through changes in the ratio between these parameters. In particular, excessive excitation damages neurons, but there are some factors that restore homeostasis (like cAMP, Interleukin-1, thyrotropin-releasing hormone). Therefore, compensatory homeostasis can, at an intermediate stage, excite neurons on the way to finding a new equilibrium point. In fig. 1. The scheme of a two-level homeostasis in a neuron is shown. Red in the figure conditionally shows damage to a neuron, and green - restoration. Damage is an external factor causing a mismatch. excessive excitation damages neurons, but there are some factors that restore homeostasis (like cAMP, Interleukin-1, thyrotropin-releasing hormone). Therefore, compensatory homeostasis can, at an intermediate stage, excite neurons on the way to finding a new equilibrium point. In fig. 1. The scheme of a two-level homeostasis in a neuron is shown. Red in the figure conditionally shows damage to a neuron, and green - restoration. Damage is an external factor causing a mismatch. excessive excitation damages neurons, but there are some factors that restore homeostasis (like cAMP, Interleukin-1, thyrotropin-releasing hormone). Therefore, compensatory homeostasis can, at an intermediate stage, excite neurons on the way to finding a new equilibrium point. In fig. 1. The scheme of a two-level homeostasis in a neuron is shown. Red in the figure conditionally shows damage to a neuron, and green - restoration. Damage is an external factor causing a mismatch. Red in the figure conditionally shows damage to a neuron, and green - restoration. Damage is an external factor causing a mismatch. Red in the figure conditionally shows damage to a neuron, and green - restoration. Damage is an external factor causing a mismatch.


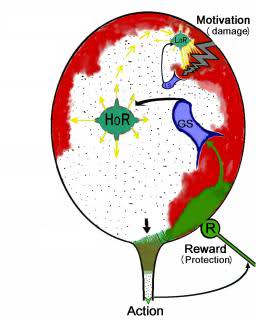
Fig. 1. Neuron
homeostasis (LoR is low-level homeostasis, HoR is high-level homeostasis, LS is a local mismatch sensor, R is a reward that reduces the mismatch level)

A set of models of homeostasis is known in the literature [3,4], but they are not oriented to self-organization of neural networks and targeted behavior. Modeling of targeted behavior, including on the basis of neural networks and reinforcement learning, also has a rich history and is widely covered in the literature. However, within the framework of these models, the homeostasis of neurons and networks as a whole was not considered.

Actually, based on the foregoing, a hierarchy of models was formulated that would constitute a complete system:
- a model of a homeostatic neuron that combines the key characteristics of known models and the basic principles of the paradigm in question;
- models of a homeostatic neural network based on homeostatic neurons;
- A model of a simple organism controlled by a homeostatic neural network and its interaction with the environment;
- modeling of the evolutionary development of simple organisms in a changing external environment.

Model of a homeostatic neuron and neural network

Since the main task is to analyze the paradigm of the homeostatic neuron as a possible basis for the mechanism of self-organization of the neural network and its ability to autonomous behavior, special attention should be paid to this key primary model. The model of a homeostatic neuron implies that each neuron seeks to maintain its optimal internal state - homeostasis, and when the current state is optimal, the neuron forms a response aimed at returning to the optimal state. As already mentioned, a change in many factors can lead to imbalance of the neuron, however, in the model situation, we introduce some unified endogenous assessment of the state of the neuron q (t) with a predetermined optimal valueq ^opt . We also introduce an indicator of the value of internal energy e (t) , which reflects the neuron's ability to generate x (t) signals and maintain homeostasis of its own activity.

The desire of a neuron to homeostasis is expressed in activity aimed at eliminating the mismatch q ^opt -q (t) , the more pronounced, the greater the mismatch. The activity of a neuron requires energy costs, therefore, it can take different forms depending on the amount of available energy e (t) .

Thus, we formulated some requirements for the model of the “egoistic” neuron, i.e. of such a neuron that has one goal - to maintain its state close to optimal. However, each neuron cannot exist in isolation, but must function in a complete neural network. Thus, we can introduce the concept of the impact vector on a specific neuron from the rest of the network:

This effect changes the endogenous assessment of the neuron by the next time step:

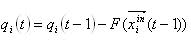
This function may look different, but the simplest case is that it


turns out that we introduced all the characteristics above neuron, as well as the methodology for determining the effect on the neuron from the remaining neurons. Now we introduce the concept of neuron mismatch g (t), the meaning of which we have already touched on above, as well as the actual concept of the action of a neuron and an output signal. Neuron mismatch:

Now we determine the action of the neuron that it chooses on the basis of the current mismatch:


At this stage it is necessary to dwell in more detail, since on the one hand it is one of the key in the whole model, and on the other hand, the very concept of action accumulates several biological principles and our thoughts, which were mentioned above.

The first thing to note is that any action on the neuron by other neurons leads to a deviation from its homeostatic equilibrium. Accordingly, all actions of our “selfish” neuron should be aimed at returning to this balance. That isprinciple of low level homeostasis . There are several possible cases, which actually were considered when compiling the function of the action.

The action of a neuron primarily depends on the degree of its inconsistency. If the neuron is far from the point of homeostatic equilibrium, then it carries out an action that immediately returns it to equilibrium - spike generation. If it is close to equilibrium, then another mechanism of homeostasis is activated - slow recovery. For each action, the neuron spends energy: on a spike - large, and on recovery - not very large. About replenishment of neuron energy will be described later.

In addition to this, the energy of the neuron may not be enough to generate a spike, even when it is necessary, which means the choice of recovery until the moment when the energy is replenished.

Thus, the action of a neuron is a function of the input signal, endogenous assessment of the state and energy reserve. Actually, this ends the formal model of the neuron (including homeostasis of the lower level) and the network as a whole. In fig. 2 is a schematic representation of a “selfish” neuron.


Fig. 2. "Selfish" neuron

Organism model

The neural network is part of the whole organism, however, for its full definition it is necessary to introduce some more additional concepts. The first of these is the common energy pool E (t) , from which the energies of all neurons in the network are restored. If e (t)min(optimal energy reserve of a neuron), then

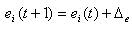
Now we need to define the concept of higher level homeostasis .
We introduce the concept of endogenous assessment of the state of the entire network:

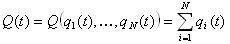
In this case, we assume that there is some optimal state Q ^opt :

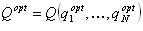
Then we determine that top-level homeostasis comes into effect in two different cases:
- after stability is established (in the event that a cyclic process is observed in the network, but the state does not reach the optimal value)
- when there is a “need” (in the case of a large mismatch of the endogenous assessment of the network state)

In this case, the parameters q _i ^optrandomly, while the magnitude of the change in each value is proportional to both the mismatch of the endogenous assessment of the state of the network and the mismatch of the endogenous assessment of a particular neuron. Thus, if the system is unable to achieve the optimal state and if the life of the entire network is threatened, the mechanism of homeostasis of the highest level is activated. Schematically, such an organism model is shown in Fig. 3.


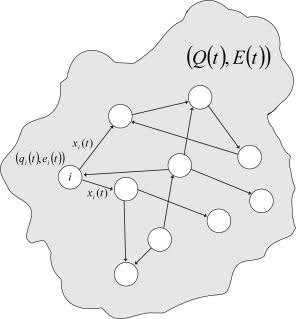
Fig. 3. Model of the organism

Here, it is probably necessary to provide some experimental data by which it will be possible to judge the qualitative dynamics of such a model (without homeostasis of the highest level). We compiled a network of 10 neurons with randomly distributed weights according to the distribution W _ij ~ N (0,1)and with various optimal values ​​of endogenous assessment of the state and energy reserve. Moreover, at the time of initialization, 9 neurons were in equilibrium, and one of the neurons was mismatched. In fig. Figures 4-5 show the time dependence of the endogenous assessment of the state and energy of each neuron in such a system.


Fig. Figure 4. Dynamics of endogenous assessment of the state of neurons


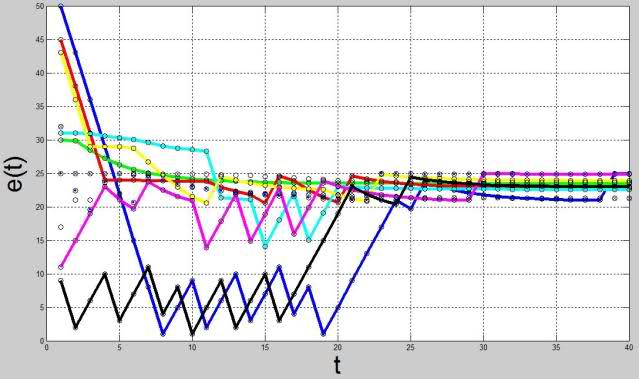
. Fig. 5. Graph of the dynamics of the energy reserve of neurons

From the figures it can be seen that, as a result, the whole system comes to the position of homeostatic equilibrium, however, our experiments show that there is a range of parameters at which achievement of homeostatic equilibrium is impossible and a self-oscillating process begins in the system, which indicates the need for inclusion top-level homeostasis.

Interaction with the environment

Imagine that we put such an organism in the environment. Suppose that our body has only one need - the need to maintain a sufficient level of total energy, which is spent on homeostasis and metabolic processes. In this case, it is necessary that the body can make a decision at the right time to replenish the energy level. That is, for example, pressing a button so that food is served to him.

We thought about introducing macro parameters of the body, the change of which determines its needs (there may be several), as well as considering a set of effectors that allow the body to change the values ​​of its macro parameters due to interaction with the environment. The proposed approach to the problem is based on the transfer of information about the values ​​of macroparameters directly to homeostatic neurons, which connects the internal homeostasis of the neuron with the satisfaction of the corresponding need. Thus, homeostasis of the second level is responsible for the operability of the system as a whole, and of the first level - for the effective line of the body's behavior when interacting with the environment.

I will explain with an example. To do this, suppose that in the structure of the neural network there are two specialized neurons.

The first neuron is specialized regarding the need for energy replenishment, that is, it enters into a mismatch if the level of total energy is insufficient. That is, he has an additional input, which receives the level of lack of total energy ( EE _min ). The second neuron is specialized regarding the execution of the energy replenishment action, that is, at the moment when it generates a spike, the total energy is replenished from the external environment. This system is shown in Fig. 6.


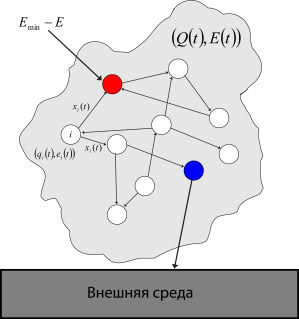
Fig. 6. The interaction of the organism with the environment; the
red neuron is specialized in relation to the need for energy replenishment, blue - in relation to the fulfillment of the energy replenishment action)

Thus, the mismatch in the body is introduced at the moment when he feels the need for food. In turn, neurons try to eliminate this mismatch. Until there is a spike on a neuron specialized with respect to the execution of an action, energy replenishment will not occur, and a signal of a lack of energy will continue to flow into the system. Thus, at some point, the spike is generated on the second specialized neuron and the total energy supply is replenished, due to which the neuron, which is specialized in the need for energy replenishment, ceases to be inconsistent.

Of course this is a very model situation, but it shows by what logic such an organism can function in an environment where some decisions are required to be made.

Continuous model

Exclusively for those who think about how to make this time-discrete model continuous, I cite our version based on the FitzHugh-Nagumo model of neurons.

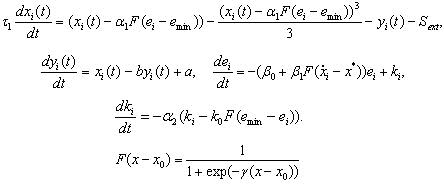
Conclusion

Of course, this model can not claim at least some kind of completeness. However, it seems to me that some of the thoughts embedded in it are quite interesting and can be the subject of research by readers. In particular, the idea of ​​a mismatch of a neuron as a motivation for performing an action, the definition of a mismatch as a ratio of the internal parameters of a neuron to a microenvironment, and homeostasis as a basis for eliminating a mismatch and for a self-organizing effect.

Also, with this topic, I wanted to draw the attention of readers to the fact that even in fairly simple models interesting effects of self-organization can arise, which in the long run can lead to holistic behavior.

I note that in this review I did not touch on the non-trivial issue of introducing the learning process into this model, as well as evolution itself. All this remains the subject of further possible research.

Authorship

Maxim Komarov (Nizhny Novgorod University), Daniil Kanevsky (VMiK MSU), Sergey Kulivets (IPU RAS), as well as your humble servant took part in the development of this model. Lev Efimovich Tsitolovsky (Bar-Ilan University, Israel) and Vladimir Georgievich Redko (NIIIS RAS) deserve great gratitude for their support and monitoring the direction of our thoughts when we were drifting. Each of us has brought to this model our thoughts and considerations from the areas we are engaged in.

List of references

[1] . Cannon WB Physical Review, 1928, 9: 399-431.
[2] . Cabanac M. Journal of Theoretical Biology, 1992, 155: 173-200.
[3] . Davis GW Annual Review of Neuroscience, 29: 307-323, 2006.
[4] . Marder A., ​​Prinz AA BioEssays, 24: 1145-1154, 2002