New Year, new records: 50th Mersenne prime found
- Transfer
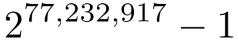
Raleigh, North Carolina, January 3, 2018 - Great Internet Mersenne Prime Search (GIMPS, a large-scale Internet project for searching Mersenne primes) discovered the largest known prime number, 2,77232,917 -1, consisting of 23,249,425 digits . The computer of the volunteer Jonathan Pace calculated it on December 26, 2017. Jonathan is one of thousands of volunteers using the free GIMPS software .
The new prime number, also known as M77232917, is calculated by multiplying 77,232,917 doubles and subtracting one. It’s about one million more digits than the previous record prime, in a special class of exceptionally rare primes known as Mersenne numbers. This is just the 50th open Mersenne prime; calculating each subsequent one becomes more difficult. Mersenne primes are named for the French monk Marina Mersenne , who studied these numbers more than 350 years ago. Founded in 1996, GIMPS discovered the last 16 Mersenne primes. Volunteers download a free program to search for these primes and have a chance to win a cash prize if they are lucky to find a new number.
Professor Chris Caldwell has an authoritative website dedicated to the largest known primes with a wonderful history of Mersenne primes .
The simplicity test took six days of non-stop computing on a PC with an Intel i5-6600 processor. To prove that there are no errors in the process of detecting primes, the new prime number is checked in four different programs on four different hardware configurations.
- Aaron Blosser tested it using Prime95 on an Intel Xeon server in 37 hours.
- David Stanfill checked the number in gpuOwL on an AMD RX Vega 64 video processor in 34 hours.
- Andreas Hoglund tested a prime using CUDALucas on an NVidia Titan Black GPU GPU in 73 hours.
- Ernst Mayer checked the number in Mlucas' own program on the 32-core Xeon server in 82 hours. Andreas Hoglund confirmed his results by driving 65 hours of Mlucas on an Amazon AWS virtual machine.
Jonathan Pace is a 51-year-old electrical engineer who lives in Germantown, Tennessee. His perseverance was finally rewarded - Jonathan had been hunting for large prime numbers with GIMPS for over 14 years. For his discovery, he received a $ 3,000 research award from GIMPS.
Prime95 client software was developed by GIMPS founder George Waltman. Scott Kurovsky wrote the PrimeNet system software coordinating GIMPS computers. Aaron Blosser now works as a system administrator and, if necessary, updates and maintains PrimeNet. Volunteers have a chance to receive a reward of $ 3,000 or $ 50,000 if their computer opens a new Mersenne prime. GIMPS 'next big goal is to win the Electronic Frontier Foundation$ 150,000 reward to be awarded for finding a prime number with 100,000,000 digits.
We are grateful for finding this prime number not only to Jonathan Pace, who executed Prime95 software on his computer: Waltman for the written software, Kurovsky and Blosser for their work with the Primenet server, as well as to thousands of GIMPS volunteers who sifted through millions of numbers. In gratitude to all these people, this discovery is officially attributed to “J. Pace, J. Waltman, S. Kurovsky, A. Blosser and colleagues. "
About Great Internet Mersenne Prime Search
Great Internet Mersenne Prime Search Organization (GIMPS)was formed in January 1996 by George Waltman to find new Mersenne prime world records. In 1997, Scott Kurovsky provided GIMPS with the ability to harness the power of thousands of conventional computers to find these “needles in a haystack.” Most GIMPS members joined the organization for the exciting opportunity of discovering a record, rare, and historic new Mersenne prime. The search for the following Mersenne primes is already ongoing. Perhaps there are fewer, but so far unexplained simple ones, and almost certainly there are more who are waiting to be discovered. Anyone with a sufficiently powerful computer can join GIMPS and become a hunter for large primes with the ability to receive a monetary reward for their discovery. All necessary software can be downloaded for free atwww.mersenne.org/download/ . GIMPS is formed as Mersenne Research, Inc., a non-profit scientific charitable organization 501 (c) (3). You can read more about this at www.mersenneforum.org and www.mersenne.org ; donations are also accepted.
Additional Information on Mersenne Primes
Prime numbers have long fascinated both amateurs and professionals in mathematics. An integer greater than one is called a prime if its sole divisors are one and it itself. First prime numbers: 2, 3, 5, 7, 11, etc. For example, the number 10 is not prime because it is divisible by 2 and 5. The Mersenne prime is a prime of the form 2 P - 1. The first Mersenne primes are 3, 7, 31 and 127, corresponding to P = 2, 3 , 5 and 7. So far, 50 Mersenne primes are known.
Mersenne primes have been the focus of number theory ever since they were first considered by Euclid around 350 BC. The man named after these numbers, the French monk Marin Mersenne(1588-1648 gg.), Created the famous hypothesis about at which values of P you can get a prime number. To confirm this hypothesis, it took 300 years and several important discoveries.
Today there are few practical applications of this prime number, which makes some wonder: “Why even look for such large primes”? Similar doubts existed several decades ago, until finally important cryptographic algorithms based on primes were developed. Another seven good reasons to look for large primes are outlined here .
Previous discoveries of Mersenne primes as part of the GIMPS were made by participants from different countries.
Chronology
In January 2016, Curtis Cooper and colleagues discovered the 49th known Mersenne prime in the United States.
In January 2013, the same Curtis Cooper and colleagues found the 48th known Mersenne prime number .
In April 2009, Odd Magnar Strindmo and colleagues discovered the 47th known Mersenne prime number in Norway.
In September 2008, Hans-Michael Elvenich and his colleagues discovered the 46th famous Mersenne prime in Germany.
In August 2008, Edson Smith and colleagues found the 45th in the United States.
In September 2006, Curtis Cooper, Stephen Boone and colleagues discovered the 44th Mersenne prime .
In December 2005, Curtis Cooper, Stephen Boone and colleagues found the 43rd Mersenne number .
In February 2005, Dr. Martin Nowak and his colleagues calculated in Germany the 42nd known Mersenne prime .
In May 2004, Josh Findlay and colleagues discovered the 41st Mersenne prime .
In November 2003, Michael Schaefer and colleagues found the 40th famous Mersenne prime in the United States.
In November 2001, Michael Cameron and colleagues calculated the 39th Mersenne prime in Canada.
In June 1999, Nyan Hajratwala and colleagues discovered the 38th Mersenne prime in the United States.
In January 1998, Roland Clarkson and colleagues discovered37th Mersenne prime in the USA.
In August 1997, Gordon Spence and colleagues found the 36th Mersenne prime in the United States.
In November 1996, Joel Armengo and colleagues discovered the 35th famous Mersenne prime in France.
In January 2013, the same Curtis Cooper and colleagues found the 48th known Mersenne prime number .
In April 2009, Odd Magnar Strindmo and colleagues discovered the 47th known Mersenne prime number in Norway.
In September 2008, Hans-Michael Elvenich and his colleagues discovered the 46th famous Mersenne prime in Germany.
In August 2008, Edson Smith and colleagues found the 45th in the United States.
In September 2006, Curtis Cooper, Stephen Boone and colleagues discovered the 44th Mersenne prime .
In December 2005, Curtis Cooper, Stephen Boone and colleagues found the 43rd Mersenne number .
In February 2005, Dr. Martin Nowak and his colleagues calculated in Germany the 42nd known Mersenne prime .
In May 2004, Josh Findlay and colleagues discovered the 41st Mersenne prime .
In November 2003, Michael Schaefer and colleagues found the 40th famous Mersenne prime in the United States.
In November 2001, Michael Cameron and colleagues calculated the 39th Mersenne prime in Canada.
In June 1999, Nyan Hajratwala and colleagues discovered the 38th Mersenne prime in the United States.
In January 1998, Roland Clarkson and colleagues discovered37th Mersenne prime in the USA.
In August 1997, Gordon Spence and colleagues found the 36th Mersenne prime in the United States.
In November 1996, Joel Armengo and colleagues discovered the 35th famous Mersenne prime in France.
Euclid proved that every prime Mersenne generates a perfect number. A perfect number is a number whose sum of its own divisors equals the number itself. The smallest perfect number is 6 = 1 + 2 + 3, the second is 28 = 1 + 2 + 4 + 7 + 14. Euler (1707-1783) proved that all even perfect numbers are the result of Mersenne primes. The last open perfect number is 2,77232,916 x ( 2,77232917 -1). This number has over 46 million digits ! It is still unknown whether there are odd perfect numbers.
The arithmetic algorithms underlying the GIMPS project have a unique history. Programs that find the latest large Mersenne primes are based on a special algorithm. In the early 1990s the now deceasedRichard Crandall , a distinguished Apple scientist, discovered ways to double the speed of a convolution - very large multiplication operations. This method is applicable not only to the search for primes, but also to other aspects of computing. In the process of working on this project, he also patented the Fast Elliptic Encryption encryption system, which is now owned by Apple Computer. It uses Mersenne primes to quickly encrypt and decrypt messages. George Waltman implemented the Crandall algorithm in assembly language, thus creating a program for finding prime numbers with unprecedented efficiency. This work led to the creation of a successful GIMPS project.
School teachers use GIMPS to get their students interested in math. Students who run software on their computers contribute to mathematical research.
Addition from the post of John D. Cook.
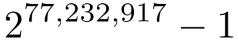
This number contains consists of 23,249,425 digits when written in decimal form.
In binary, 2 p - 1 is a sequence of p units. For example, 31 = 2 5 - 1 equals 11111 in binary form. That is, in binary form, the new record prime is a string of 77,232,917 units.
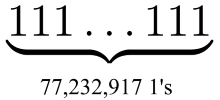
A binary number can be converted to hexadecimal (base 16), starting from the right end and converting blocks of four bits into hexadecimal numbers. For example, to convert 101101111 to HEX, we will divide the number into three blocks: 1, 0110 and 1111. These blocks are converted to 1, 6 and F, that is, binary 101101111 corresponds to 16F hexadecimal.
Further, 77,232,917 = 19,308,229 * 4 + 1, that is, we split our line of 77,232,917 units into groups of four digits, getting one remaining bit, followed by 19,308,229 groups of four digits. This means that in hexadecimal notation, the new record prime is 1FFF ... FFF - the unit followed by 19,308,229 F.
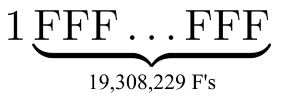
The new record is the 50th Mersenne prime. The Mersenne prime is a prime one less than the power of two, i.e. has the form 2 p - 1. It turned out that for simplicity 2 p - 1, the number p should also be prime. In the case of a new record, 77,232,917 is simple.
It is not known whether there are an infinite number of Mersenne primes. But now we know that there are at least 50 of them.
All the last records of primes were Mersenne numbers, because there is an algorithm for checking whether a number of the form 2 p - 1 is prime ( Luke-Lemer test ).
