Julia and the swarm of particles
- Tutorial
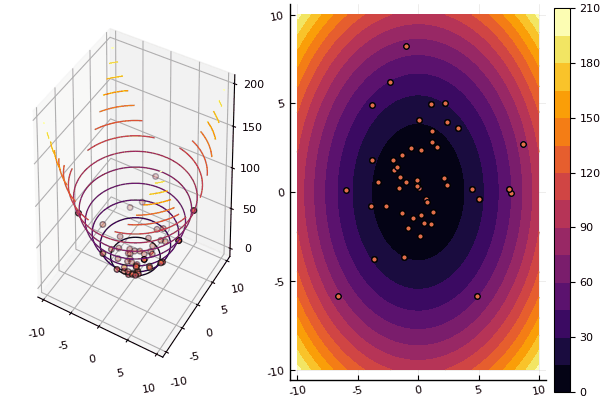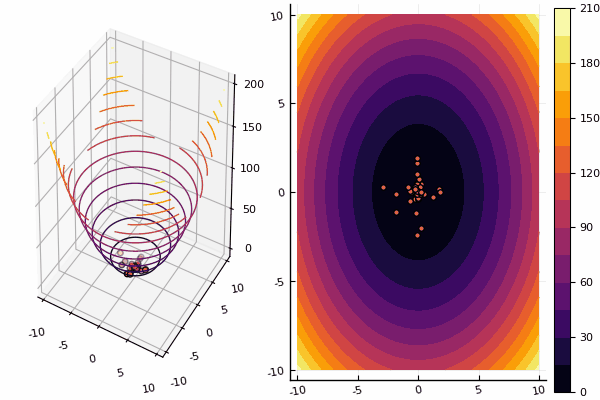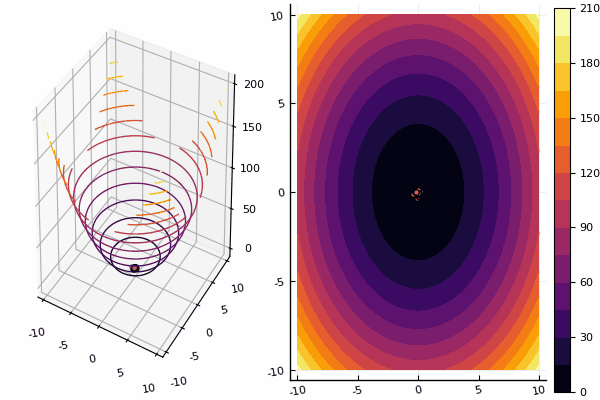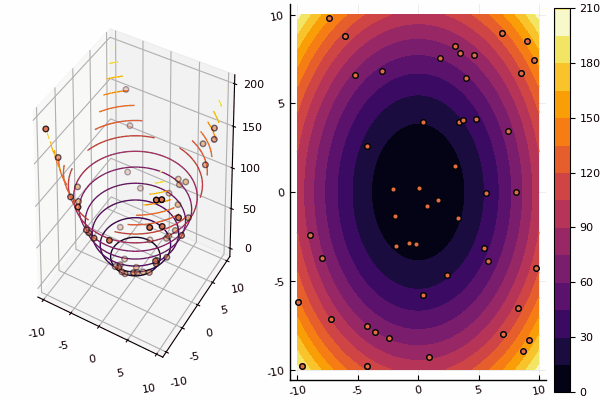
We continue to study methods of multidimensional optimization, and the next in line is the particle swarm method searching for a global minimum.
Theory
- Wikipedia
- Different methods of particle swarming and their topologies
- Swarm of particles in Python and C #
- Method for optimizing a pack of cats
The algorithm is pretty simple:

The position of each particle at a certain moment is calculated by the formula:
Where - coordinate of the best solution of a particular particle,
- coordinate of the best solution for all particles for this era,
and
- weight coefficients (selected for a specific model),
- the coefficient of inertia, it can be made dependent on the number of the epoch, then the speed of the particles will vary smoothly.
Test functions
Since it is very pleasant to look at the work of the method, we will get more test functions:
parabol(x) = sum(u->u*u, x)
# f(0,0) = 0, x_i ∈ [-10,10]
shvefel(x) = sum(u-> -u*sin(sqrt(abs(u))), x)
# f(420.9687,420.9687) = -819?, x_i ∈ [-500,500]
rastrigin(x) = 10*length(x) + sum(u->u*u-10*cos(2*pi*u), x)
# f(0,0) = 0, x_i ∈ [-5,5]
ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ
# f(0,0) = 0, x_i ∈ [-5,5]
rosenbrok(x) = 100(x[2]-x[1]*x[1])^2 + (x[1]-1)^2# f(0,0) = 0, x_i ∈ [-5,5]
bill(x) = (1.5-x[1]+x[1]*x[2])^2 + (2.25-x[1]+x[1]*x[2]*x[2])^2 + (2.625-x[1]+x[1]*x[2]^3)^2# f(3,0.5) = 0, x_i ∈ [-5,5]
boot(x) = (x[1]+2x[2]-7)^2 + (2x[1]+x[2]-5)^2# f(1,3) = 0, x_i ∈ [-10,10]
bukin6(x) = 100sqrt(abs(x[2]-0.01x[1]*x[1])) + 0.01abs(x[1]+10)
# f(-10,1) = 0, x_i ∈ [-15,-5; -3,3]
levy13(x) = sinpi(3x[1])^2 + (1+sinpi(3x[2])^2)*(x[1]-1)^2 + (1+sinpi(2x[2])^2)*(x[2]-1)^2# f(1,1) = 0, x_i ∈ [-10,10]
himmelblau(x) = (x[1]^2+x[2]-11)^2 + (x[1]+x[2]^2-7)^2# f(3,2)... = 0, x_i ∈ [-5,5]
camel3humped(x) = 2x[1]^2 - 1.05x[1]^4 + x[1]^6 /6 + x[1]*x[2] + x[2]^2# f(0,0) = 0, x_i ∈ [-5,5]
izom(x) = -cos(x[1])*cos(x[2])*exp(-( (x[1]-pi)^2 + (x[2]-pi)^2 ))
# f(π,π) = -1, x_i ∈ [-100,100]
holdertable(x) = -abs(sin(x[1])*cos(x[2])exp(abs( 1-sqrt(x[1]^2+x[2]^2)/pi )))
# f(±8.05502,±9.66459) = -19.2085, x_i ∈ [-10,10]
shaffer4(x) = 0.5 + (cos(sin(abs(x[1]^2-x[2]^2)))^2-0.5) / (1+0.001(x[1]^2+x[2]^2))^2# f(0,1.25313) = 0.292579, x_i ∈ [-100,100]And, actually, MUF itself:
function mdpso(;
nparts = 50,
ndimes = 2,
ages = 50, # количество эпох
lover = [-10-10],
upper = [1010],
C1 = [1.91.9], # весовые коэф-ты
C2 = [1.81.8],
Ac = [0.10.1],
)
minind = 0
V = zeros(nparts,ndimes) # матрица нулей n на n
X = zeros(nparts,ndimes)
funmin = -Inf
Fmin = Inf
Fbest = fill(Fmin, nparts)
funx = zeros(nparts)
xmem = zeros(nparts,ndimes)
xbest = zeros(ndimes) # лучшая координата# частицы разбрасываются по исследуемой областиfor i in1:nparts, j in1:ndimes
X[i,j] = randomer(lover[j], upper[j])
end
for i in1:ages
for j in1:nparts
funx[j] = fun(X[j,:])
if funx[j] < Fbest[j]
Fbest[j] = funx[j]
xmem[j,:] = X[j,:]
end
end
# отрисовывает частицы на каждой эпохе
ploter(lover, upper, X, funx, i);
funmin = minimum(funx)
minind = argmin(funx)
if funmin < Fmin
Fmin = funmin
xbest[:] = X[minind,:]
end
for j in1:nparts, k in1:ndimes
R1 = rand()
R2 = rand()
V[j,k] = Ac[k]*V[j,k] + C1[k]*R1*(xmem[j,k] - X[j,k]) +
C2[k]*R2*(xbest[k] - X[j,k])
X[j,k] += V[j,k]
end
println("Age № $i\n xbest:\n $(xbest[1]) $(xbest[2])")
println("Fmin: $Fmin\n")
end
f = open("$fun.txt","w") # выводим параметры модели в файл
write(f,"C1 = $C1, C2 = $C2, Ac = $Ac, lower = $lover, upper = $upper, ages = $ages, parts = $nparts")
close(f)
endWith drawings, though, the calculation is performed longer, but more beautiful:
using Plots
pyplot()
function ploter(l, u, xy, z, n_age )
contour(Xs, Ys, Zs, fill = true);
# легенду не показывать (для каждой блин частицы)# задать границы рисунка, чтоб не дергалось кода частица убежала
scatter!(xy[:,1], xy[:,2], legend = false, xaxis=( (l[1], u[1])), yaxis=( (l[2], u[2])) );
#savefig("$fun $n_age.png") # создаёт кадры эпох в папке с проектом
end
fun = bill
low = [-4-4]
up = [44]
Xs = range(low[1], stop = up[1], length = 80)
Ys = range(low[2], stop = up[2], length = 80)
Zs = [ fun([x y]) for y in Ys, x in Xs ]
surface(Xs, Ys, Zs)
xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] )
yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] )
mdpso(C1 = [1.21.2], C2 = [1.11.1], Ac = [0.080.08], lower = [-4-4], upper = [44], ages = 30)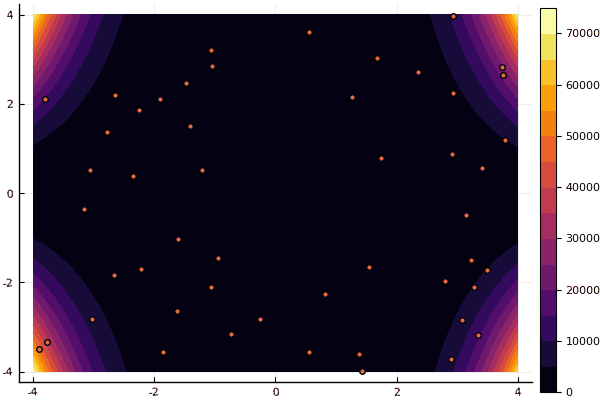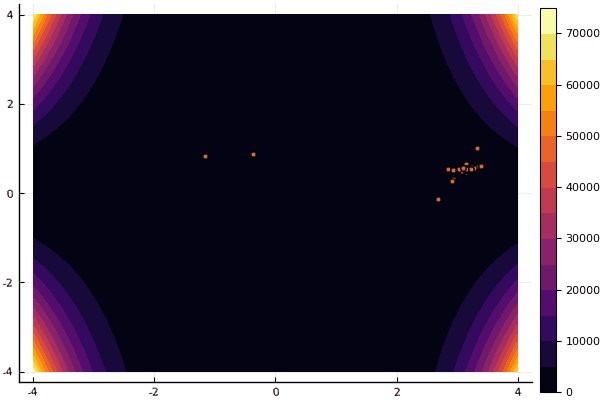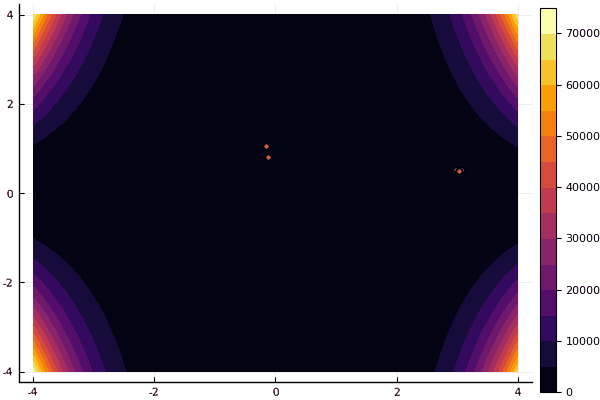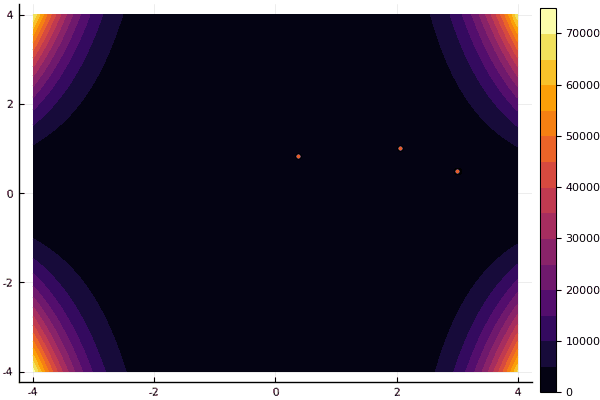
fun = ekly
mdpso(C1 = [1.71.7], C2 = [1.71.7], Ac = [0.070.07], lower = [-5-5], upper = [55], ages = 15)

fun = himmelblau
mdpso(C1 = [1.11.1], C2 = [1.01.0], Ac = [0.090.09], lower = [-5-5], upper = [55], ages = 20, parts = 50)
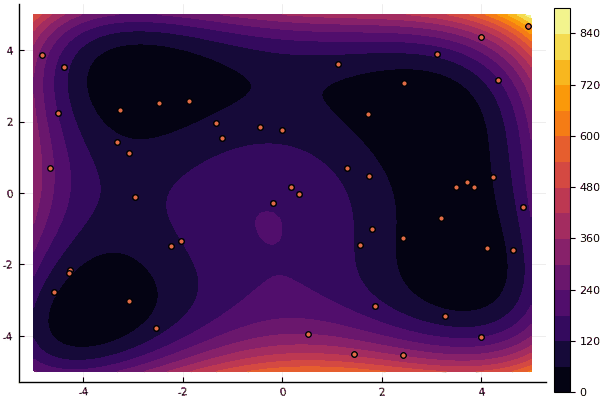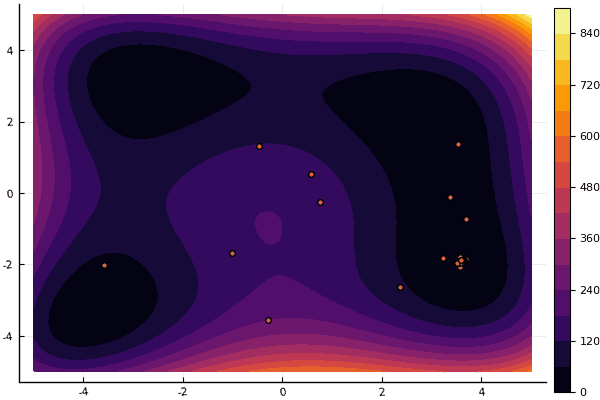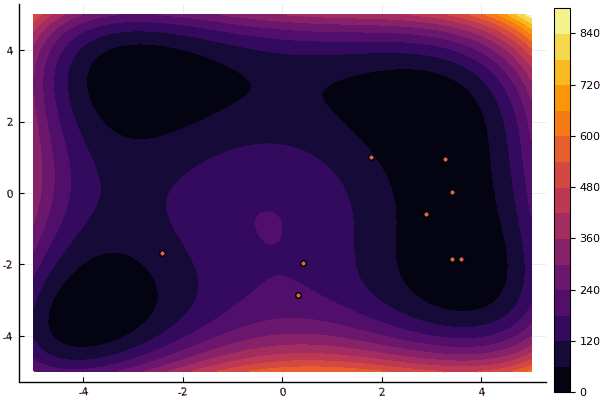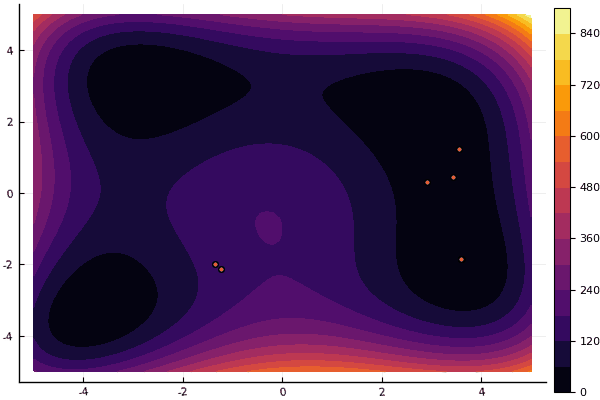
fun = holdertable
mdpso(C1 = [1.11.1], C2 = [1.01.0], Ac = [0.090.09], lower = [-10-10], upper = [1010], ages = 20, parts = 50)

fun = levy13
mdpso(C1 = [1.11.1], C2 = [1.01.0], Ac = [0.090.09], lower = [-10-10], upper = [1010], ages = 20, parts = 50)
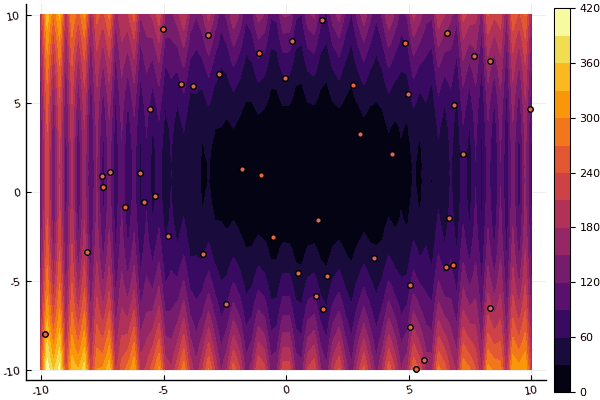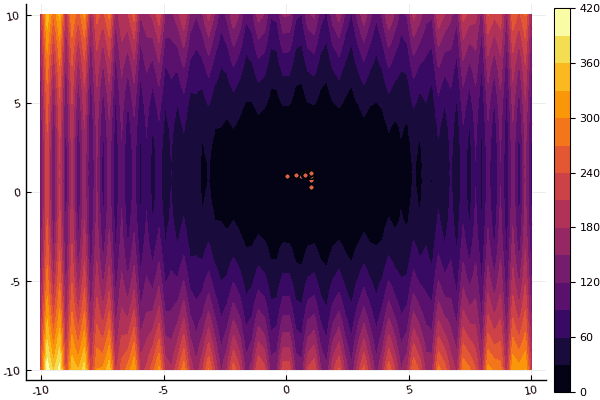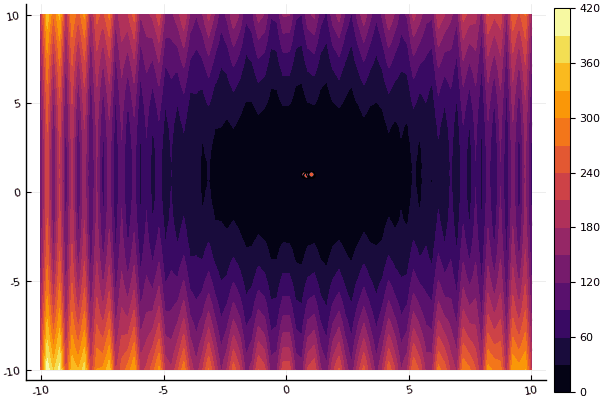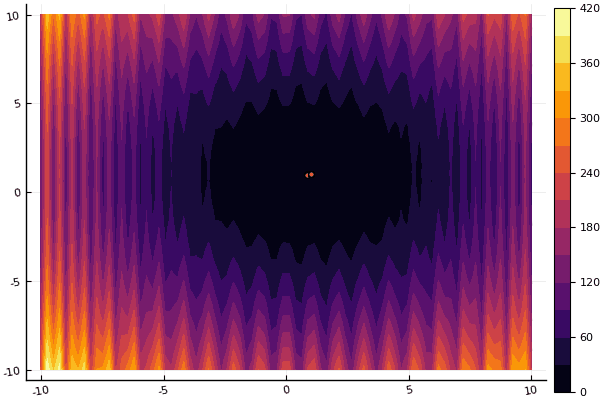
fun = shaffer4
mdpso(C1 = [1.11.1], C2 = [1.01.0], Ac = [0.090.09], lower = [-100-100], upper = [100100], ages = 20, parts = 50)
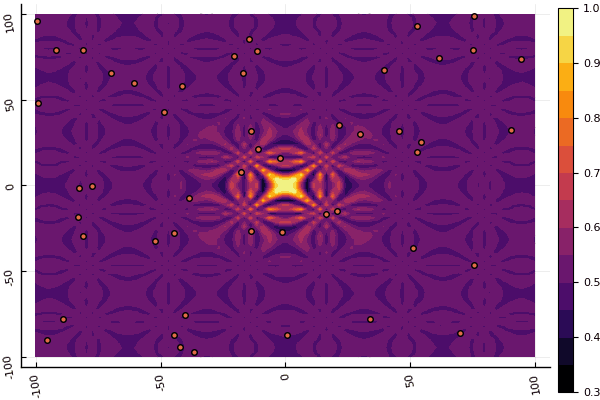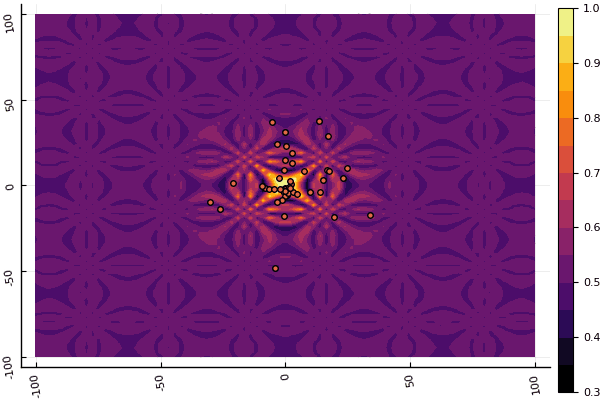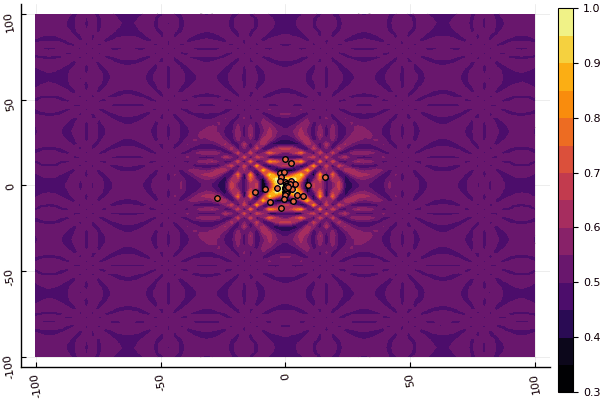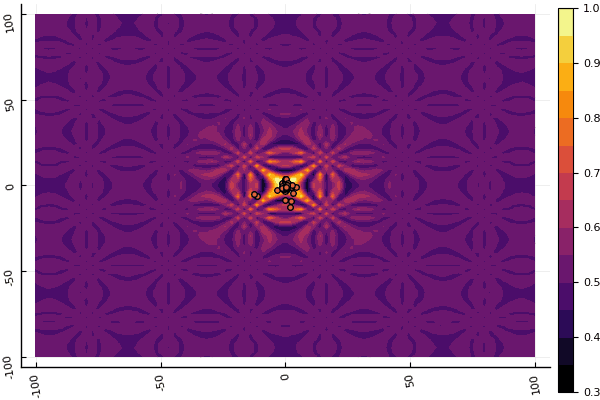
What is really depressing is the fussing with the parameters and the element of chance: if not a single particle flew past the global minimum, then the whole thing could fall into a local one:
fun = rastrigin
mdpso(mdpso(C1 = [0.10.1], C2 = [11], Ac = [0.080.08], lover = low, upper = up, ages = 30))
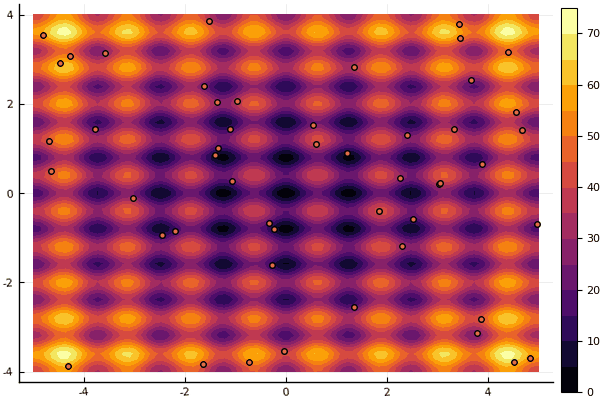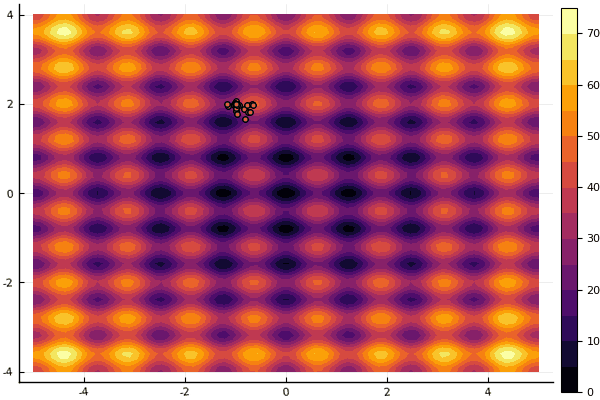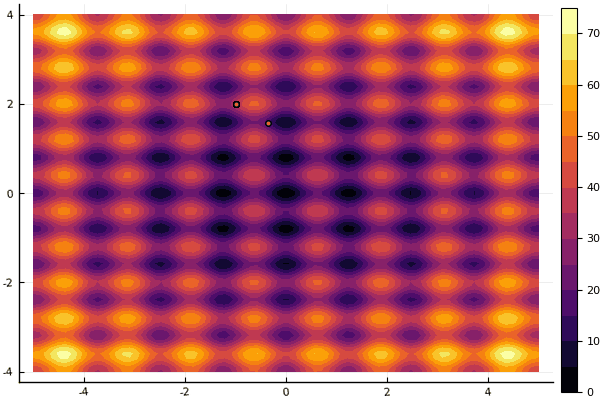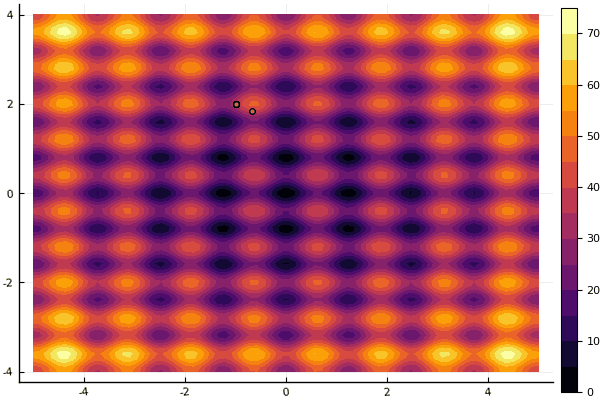
And old Not really Good Rosenbrock still does not allow himself to be comprehended:
fun = rosenbrok
mdpso(C1 = [1.71.7], C2 = [1.51.5], Ac = [0.150.15], lover = low, upper = up, ages = 20, nparts = 50)
...
Age № 20
xbest:
0.377964213418868660.12799160066705667
Fmin: 0.409026370833564
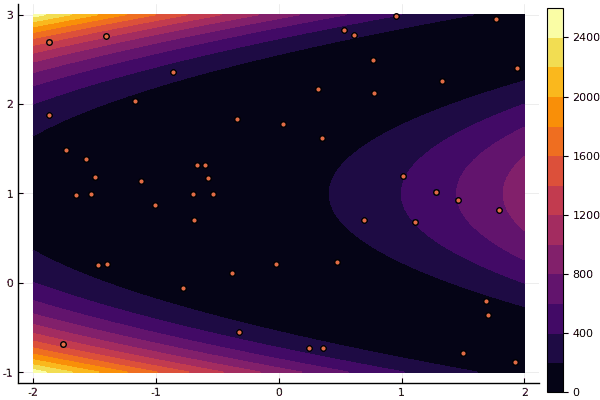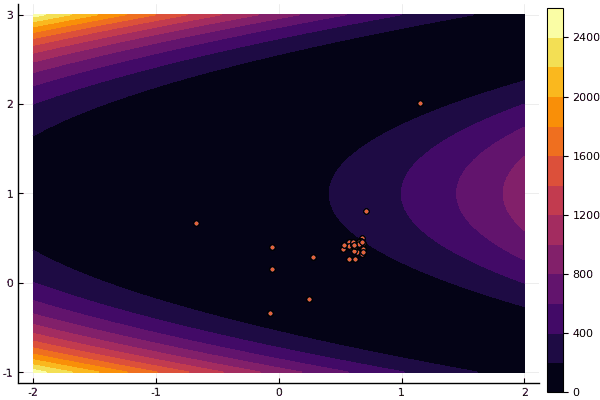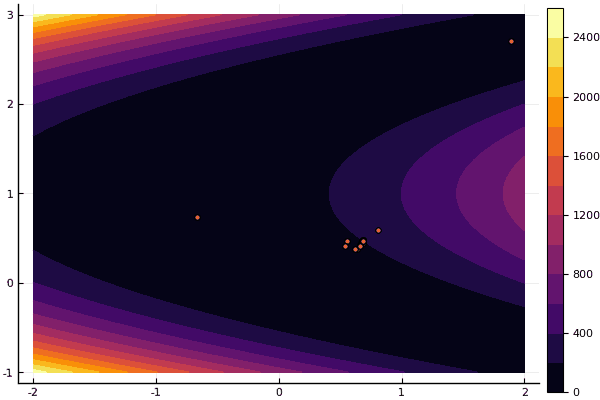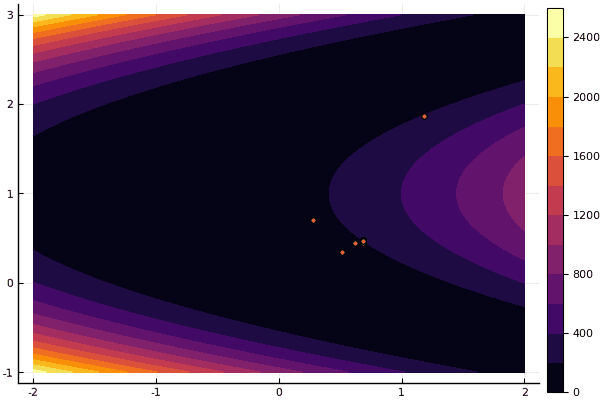
But as I said earlier, it is possible to use the MF to find a good approximation to the global minimum, and then specify, for example, Nelder-Mead:
vecl(x) = sqrt( sum(u -> u*u, x) )
function sortcoord(Mx)
N = size(Mx,2)
f = [fun(Mx[:,i]) for i in1:N] # значение функции в вершинах
Mx[:, sortperm(f)]
end
function normx(Mx)
m = size(Mx,2)
D = zeros(m-1,m)
for i = 1:m, j = i+1:m
D[i,j] = vecl(Mx[:,i] - Mx[:,j]) # считает длину разности столбцов
end
D
sqrt(maximum(D))
end
function ofNelderMid(; ndimes = 2, ε = 1e-4, fit = [.1, .1], low = [-1-1], up = [11])
k = 0
N = ndimes
dz = zeros(N, N+1)
Xx = zeros(N, N+1)
for i = 1:N+1
Xx[:,i] = fit
end
for i = 1:N
dz[i,i] = 0.5*vecl(fit)
end
Xx += dz
p = normx(Xx)
while p > ε
k += 1
Xx = sortcoord(Xx)
Xo = [ sum(Xx[i,1:N])/N for i = 1:N ] # среднее эл-тов i-й строки
Ro = 2Xo - Xx[:,N+1]
FR = fun(Ro)
if FR > fun(Xx[:,N+1])
for i = 2:N+1
Xx[:,i] = 0.5(Xx[:,1] + Xx[:,i])
end
elseif FR < fun(Xx[:,1])
Eo = Xo + 2(Xo - Xx[:,N+1])
if FR > fun(Eo)
Xx[:,N+1] = Eo
else
Xx[:,N+1] = Ro
end
elseif FR <= fun(Xx[:,N])
Xx[:,N+1] = Ro
else
Co = Xo + 0.5(Xo - Xx[:,N+1])
if FR > fun(Co)
Xx[:,N+1] = Co
else
Xx[:,N+1] = Ro
end
end
end
end
println(k, " ", p, " ", Xx[:,1])
p = normx(Xx)
end #while
fit = Xx[:,1]
endofNelderMid(fit = [0.377960.127992])
...
920.00022610400555036366 [1.0, 1.0]
930.00015987967588703512 [1.0, 1.0]
940.00011305200343052599 [1.0, 1.0]
2-element Array{Float64,1}:
0.99999999966459730.9999999995466575For a classic SMF, not everything is clear with the stopping criterion: the best point can hold a position for several epochs, the distances between some particles can also not change for a long time. Therefore, a limit on the number of epochs is used. In order to increase the chances of finding a global minimum, it is necessary to increase the number of particles and epochs, which is very expensive in terms of memory and, especially, time.
Morality
- If you do not want or can not use complex and modern methods, you can use the composition of methods easier
- Very often there is a narrow method for the task (for example, for gully functions)
- It is advisable to have on hand several different MOs for consistent comparison.
- It is not always possible to stick your task into the method and immediately get the right answer - you should spend time researching, varying the parameters, if you can’t see the relief, you should at least print out intermediate calculations to track convergence.
That's all for today, thank you for your attention and wish you all a good optimization!
