The beauty of numbers. Mathematical constants in nature

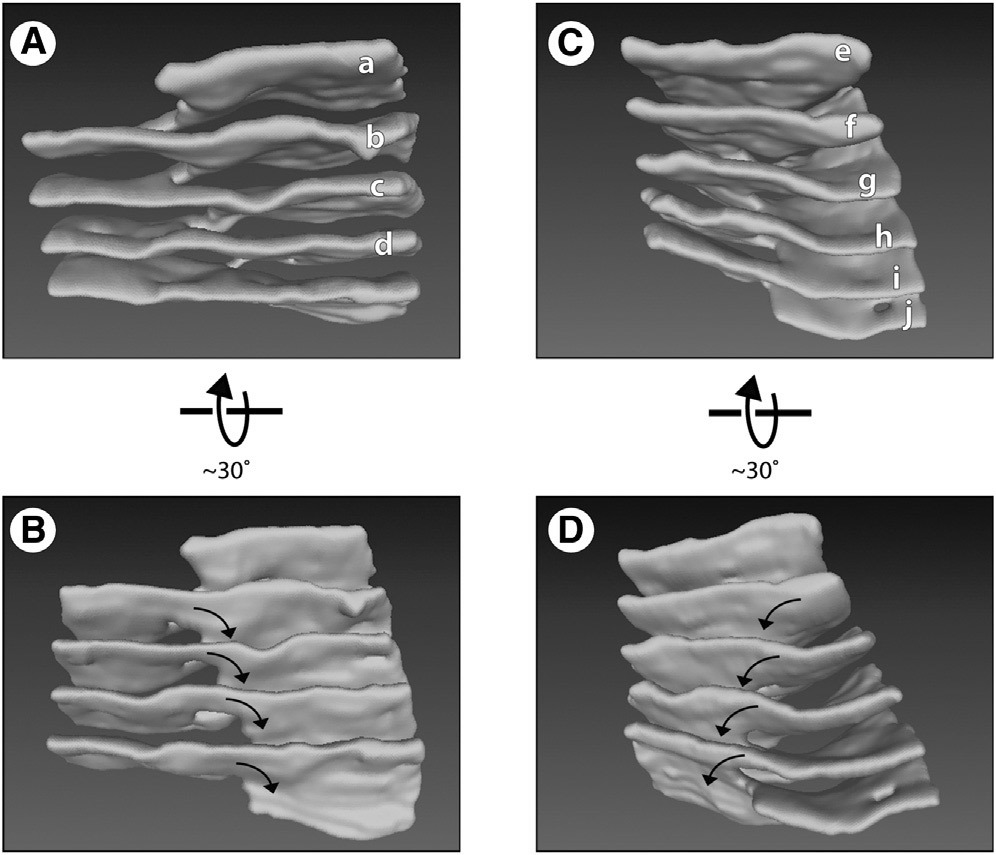
A 3D model of the endoplasmic reticulum of a eukaryotic cell with Terasaki ramps that connect the flat sheets of the membrane

In 2013, a group of molecular biologists from the United States investigated a very interesting form of the endoplasmic reticulum - the organoid inside the eukaryotic cell. The membrane of this organoid consists of flat sheets connected by spiral "ramps", as if calculated in a 3D modeling program. These are the so-called Terasaki ramps. Three years later, the work of biologists was noticed by astrophysicists. They were amazed: after all, precisely such structures are present inside neutron stars. The so-called "nuclear paste" consists of parallel sheets connected by spiral shapes.

The amazing structural similarity of living cells and neutron stars - where did it come from? Obviously, there is no direct connection between living cells and neutron stars. Just a coincidence?


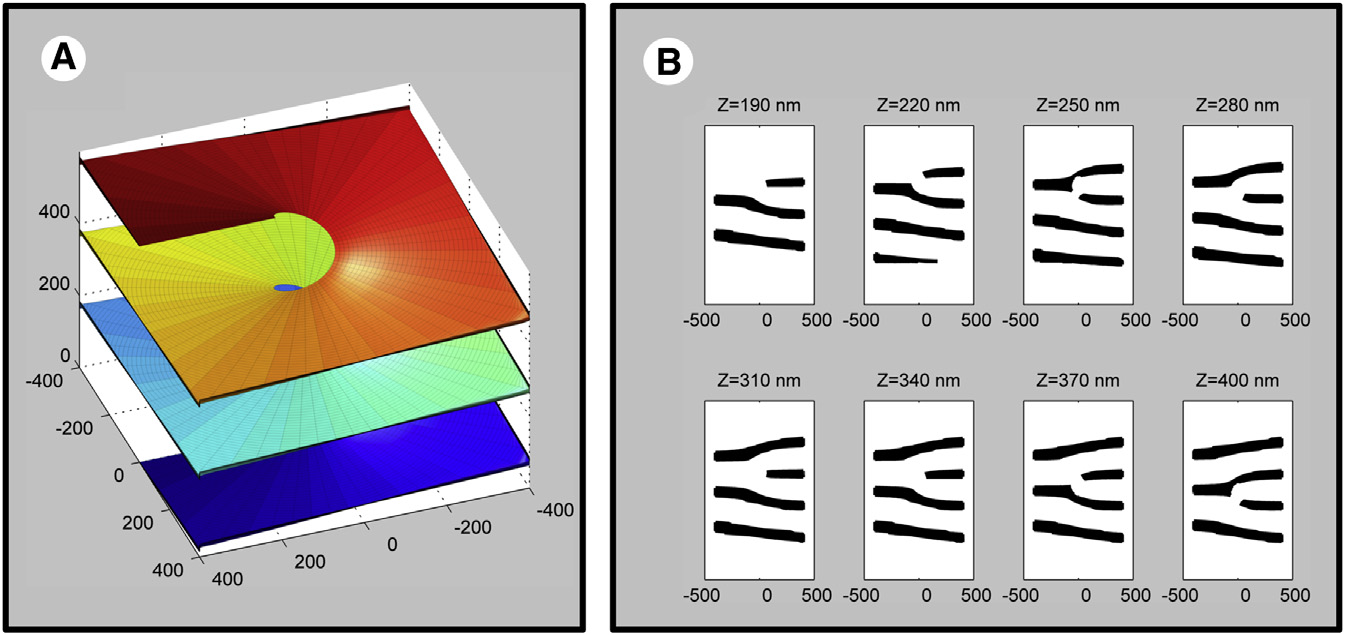
Model of spiral connections between flat membrane sheets in a eukaryotic cell

There is an assumption that the laws of nature act on all objects of the micro- and macrocosm in such a way that some of the most optimal forms and configurations appear as if by themselves. In other words, the objects of the physical world obey the hidden mathematical laws that underlie the entire universe.

Let's look at a few more examples that support this theory. These are examples where essentially different material objects exhibit similar properties.

For example, acoustic black holes, first observed in 2011, exhibit the same properties that real black holes should have in theory. In the first experimental acoustic black hole, a Bose-Einstein condensate of 100 thousand rubidium atoms was untwisted to a supersonic speed in such a way that some parts of the condensate crossed the sound barrier, while the neighboring ones did not. The boundary of these condensate parts simulated a black hole event horizon, where the flow velocity is exactly equal to the speed of sound. At temperatures near absolute zero, sound begins to behave like quantum particles - phonons(a fictitious quasiparticle represents a quantum of vibrational motion of crystal atoms). It turned out that a “sound” black hole absorbs particles in the same way as a real black hole absorbs photons. Thus, the flow of fluid acts on sound in the same way that a real black hole acts on light. In principle, a sonic black hole with phonons can be considered as a peculiar model of true curvature in space-time.

If you look more broadly at the structural similarities in various physical phenomena, you can see an amazing order in natural chaos. All diverse natural phenomena are, in fact, described by simple basic rules. Mathematical rules.

Take the fractals. These are self-similar geometric forms that can be divided into parts so that each part is at least approximately a reduced copy of the whole. One example is the famous Barnsley fern.



Barnsley fern is built using four affine transformations of the form:



This particular leaf is generated with the following coefficients:









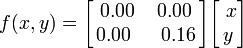
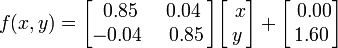
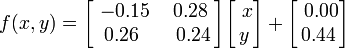
In our environment, such mathematical formulas are found everywhere - in clouds, trees, mountain ranges, ice crystals, flickering flames, in the sea coast. These are examples of fractals, the structure of which is described by relatively simple mathematical calculations.

Galileo Galilei in 1623 said: “All science is written in this great book - I mean the Universe - which is always open to us, but which cannot be understood without learning to understand the language in which it is written. And it is written in the language of mathematics, and its letters are triangles, circles and other geometric figures, without which it is impossible for a person to make out any of her words; without them, he is like wandering in darkness. ”

In fact, mathematical rules manifest themselves not only in the geometry and visual outlines of natural objects, but also in other laws. For example, in the nonlinear dynamics of the population, the growth rate of which decreases dynamically when approaching the natural limit of the ecological niche. Or in quantum physics.

As for the most famous mathematical constants - for example, the number pi - it is quite natural that it is widely found in nature, because the corresponding geometric shapes are the most rational and suitable for many natural objects. In particular, the number 2π became the fundamental physical constant. It shows what the angle of rotation in radians is, which is contained in one full revolution when the body rotates. Accordingly, this constant is everywhere found in the description of the rotational form of motion and angle of rotation, as well as in the mathematical interpretation of oscillations and waves.

For example, the period of small natural vibrations of a mathematical pendulum of length L motionless suspended in a uniform gravitational field with gravitational acceleration g is



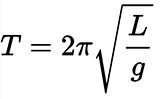
Under conditions of the Earth's rotation, the plane of oscillation of the pendulum will slowly rotate in the direction opposite to the direction of the Earth's rotation. The rotation speed of the oscillation plane of the pendulum depends on its geographical latitude .



The pi number is an integral part of the Dirac constant - the reduced Planck constant, the main constant of quantum physics, which connects two systems of units - quantum and traditional. It relates the magnitude of the energy quantum of any linear oscillatory physical system with its frequency.



Accordingly, the number pi is included in the fundamental postulate of quantum mechanics - the Heisenberg uncertainty principle.



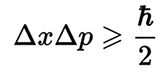
The number pi is used in the fine structure constant formula- another fundamental physical constant characterizing the strength of electromagnetic interaction, as well as in hydromechanics formulas, etc.

In the natural world, you can find other mathematical constants. For example, the number e , the base of the natural logarithm. This constant is included in the formula for the normal probability distribution, which is given by the probability density function: The



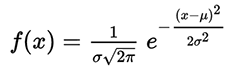
normal distribution is subject to many natural phenomena, including many characteristics of living organisms in a population. For example, the size distribution of organisms in a population: length, height, surface area, weight, blood pressure in humans and much more.

A close observation of the world around us shows that mathematics is not at all a dry abstract science, as it might seem at first glance. Quite the contrary. Mathematics is the foundation of the whole living and nonliving world around. As Galileo Galilei correctly noted, mathematics is the language that nature speaks to us.