Tuning vias for printed circuit boards
Let's talk about the design of vias - for serious electronics, their quality is very important. At the beginning of the article, I highlighted the factors affecting the integrity of the signal, and then showed examples of calculating and tuning the impedance of single and differential vias.

Hello everyone, my name is Vyacheslav. I have been developing printed circuit boards for 5 years, and during this time I not only read a lot of rules and recommendations for tracing, but also found the sources and worked with them.
In the complex computing systems that he is developingYADRO company, high-speed signals on the way from the transmitter to the receiver cover significant distances, passing through several boards and making a dozen interlayer transitions. Under such conditions, each carelessly designed vias will make a small contribution to signal degradation, and as a result, the interface may not work.
Vias (hereinafter p / o, English via) are heterogeneities in the transmission line. Like other heterogeneities, they spoil the signal. This effect is weakly expressed at low frequencies, but increases significantly with increasing frequency. Often, developers undeservedly pay little attention to the structure of vias: they can be copied from a "neighboring" project, taken from a datasheet, or not specified at all in CAD (the default setting).
Before using the calculated structure, it is necessary to understand why it was made just like that? Blind repetition can only do harm.
The integrity of the signal in the channel when passing through vias is mainly affected by the following factors:
Let us consider in more detail the causes of these effects and methods for their elimination.
In an ideally designed board, the wave impedance does not change throughout the route, including when switching to another layer. In reality, it usually looks something like this:
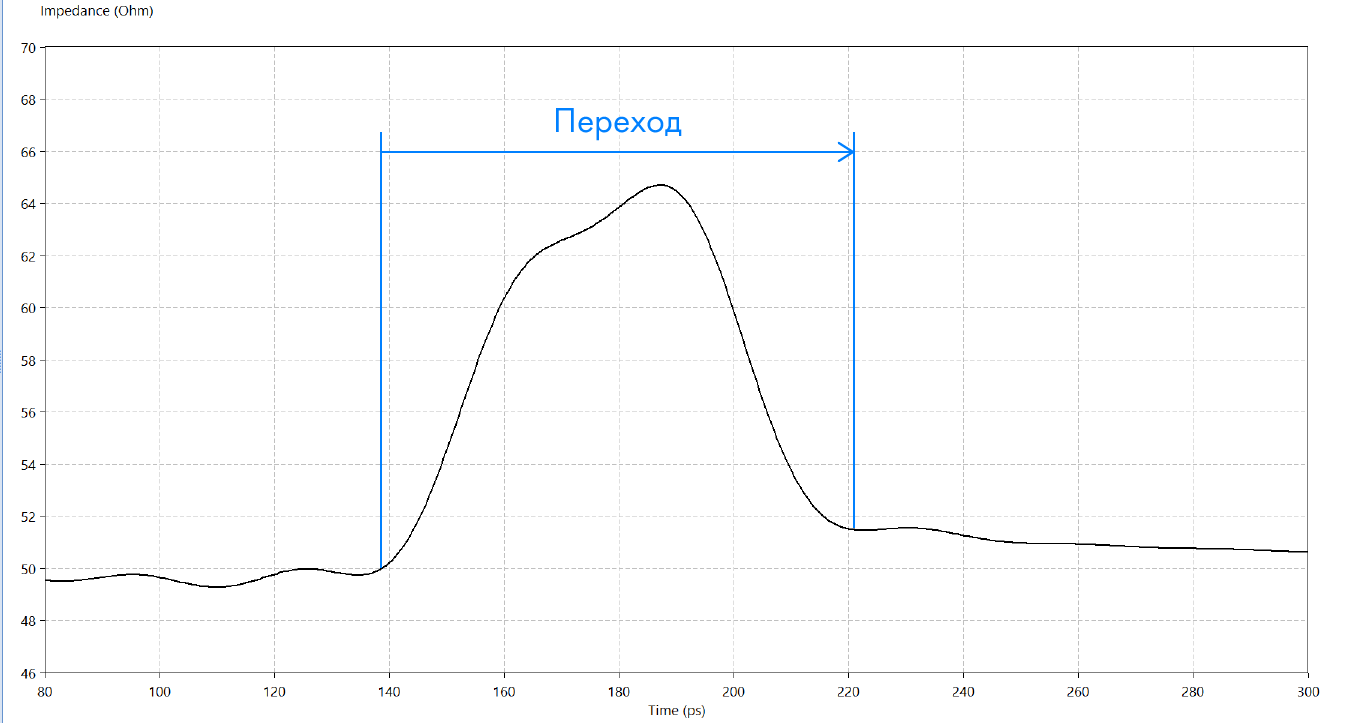
Figure 1. Change in wave impedance upon transition to another layer.
The better the wave resistances are matched, the less will be the reflection of the signal. How to influence this?
Consider the structure of p / o on the board [1].

Figure 2. Structure p / o on the board.
By changing the p / o elements, we change the wave resistance of the transition. Our goal is to match the impedance of the transition structure with the impedance of conductors to minimize reflections. Let us consider how the impedance changes when the elements of the p / o structure change.
Conductors on a printed circuit board can be made with a wave resistance lying in a wide range, but most often it is 50 Ohms. On the one hand, this is due to historical continuity: the 50 Ohm impedance was standardized for coaxial cables as a compromise between the driver load level and the signal energy loss. On the other hand, a 50-Ohm conductor is easy to fabricate on a standard board.
For the developer, it is important not so much the specific value of the wave resistance as its constancy throughout the entire transmission line.
In order to make a transmission line with a fixed value of wave impedance, the developer selects the width of the track and the distance to the reference layer, i.e. changes the linear capacity and inductance of the transmission line to a certain value.
In p / o, the inductive component is quite significant. In a first approximation, we must, within a reasonable framework, minimize the stray inductance as much as possible, and then change the p / o parameters to achieve a given capacitance, and therefore impedance.
An excessive decrease in the capacitance of a half-wave will cause a local increase in impedance and, as a consequence, signal reflections.
What happens when a signal passes through a stub through hole?

Figure 3. Transition hole with stub, resonance at ¼ wavelength.
In our example, the signal propagates from top to bottom from the Top layer. Having reached the inner signal layer, the signal is separated: part moves along the path on the inner layer, and part continues to move down the vias, then it is reflected from the Bottom layer. After the reflected signal has reached the inner layer, it is again divided, part moves along the path, and part returns to the source.
The reflected signal will be summed with the original and distort it, which will be expressed in narrowing the window on the eye diagram, and increasing the level of insertion loss (Eng. Insertion Loss).
In the worst case, the TD segment will be equal to ¼ of the wavelength of the signal, then the reflected signal will reach the path on the inner layer with a delay of half the period, overlapping the original signal in antiphase.
When analyzing the integrity, it is recommended to consider the bandwidth with a width of 5 Nyquist frequencies. A good approximation would be considered acceptable stub, giving a resonance at 7 harmonics and above [2].
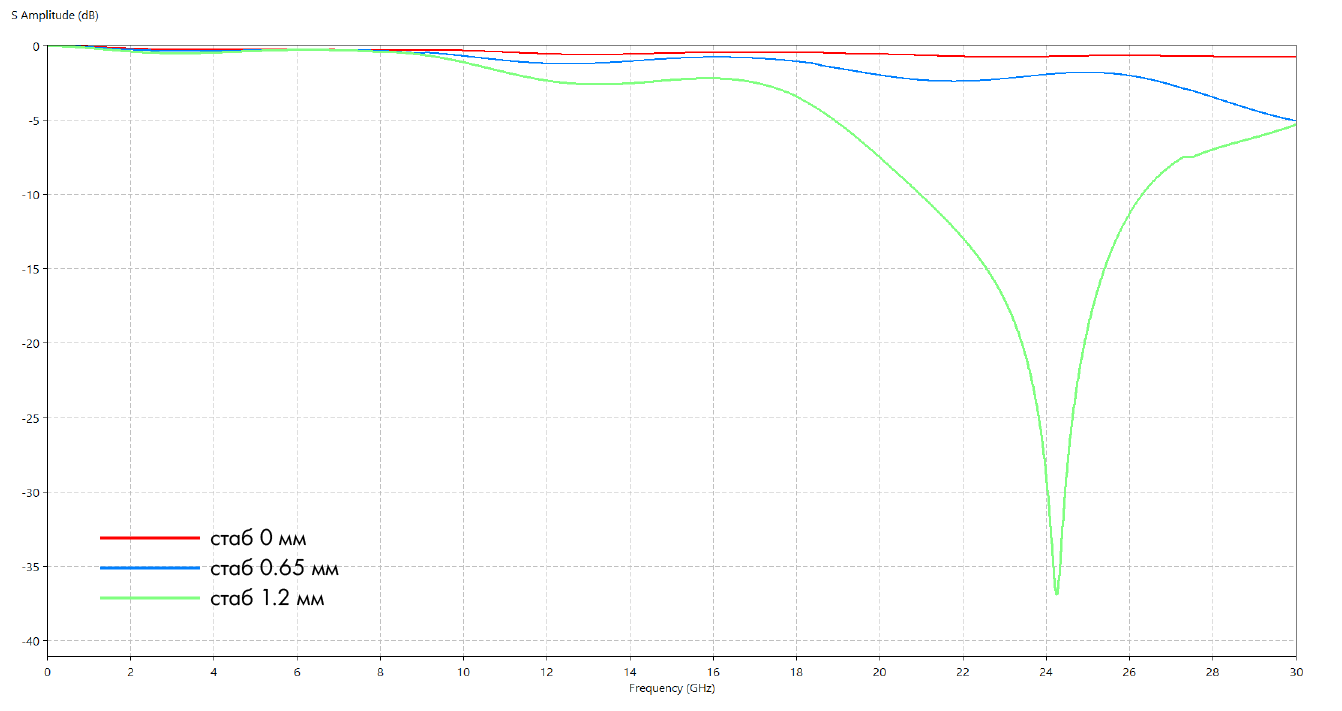
Figure 4. Graph of the level of insertion loss for p / o with stubs 0, 0.65, 1.2 mm.
Figure 4 shows a huge resonance at frequencies around 24 GHz. We can conclude that if our signal operates at a frequency of 2-3 GHz, we can afford not to eliminate the stub, because within 7 harmonics “everything is calm”.
You can make a quick assessment of the criticality of the stub in the Polar calculator.:


Figure 5. Image from polarinstruments.com . A stub length of 2.5 mm is acceptable for signals with rise times of more than 500 ps.
The formulas given in the article [2] give a slightly more accurate result. They take into account p / o geometry and allow calculating the correction for the dielectric constant of the dielectric along the Z axis.
You can remove the stub using the “backdrilling” operation (English Backdrilling), or using micro-transitions (English blind and buried vias). The choice depends on the features of the project. Reverse drilling is easier and cheaper. After manufacturing the board, with a larger diameter drill, the stub is drilled to a predetermined depth. The developer is required to specify additional indentation of the topology in the drilling zone, and it is also available for the manufacturer to indicate the drilling requirements in the design documentation. Modern CAD systems support this functionality.
Micro-junctions are primarily intended for high-density boards (English HDI), however, in some cases they can be used by leveling the high cost of refusing to drill back and reducing the number of layers on the board. When developing HDI boards, there are a few things to keep in mind:
It is highly recommended that the board structure be agreed with the manufacturer in advance.
Crosstalk - unwanted signal transmission from one line to the next. This transfer occurs because two closely spaced conductors have capacitive and inductive coupling.
The nature of the crosstalk of signal conductors and p / o is slightly different.
The signal does not have a reference layer in the n / a, the return currents flow along the adjacent n / a, forming a large loop. Crosstalk of signals in the n / a due to the inductive component.
The greatest effect on minimizing crosstalk can be achieved by increasing the distance between p / o. However, often the topologist does not have much space.
The convergence of p / o in the differential pair not only reduces the occupied area, but also has a positive effect on noise immunity [3].
A common way to minimize crosstalk between adjacent signal p / o is to place a shielding p / o between them. With this method, it will be necessary to conduct signals in increments of about 2 mm (Figure 6). If there is not enough space, you can use a smaller step with a shift (English Staggered pattern), as in Figure 7. Using simulation, you can choose the ideal angle of shift [4].
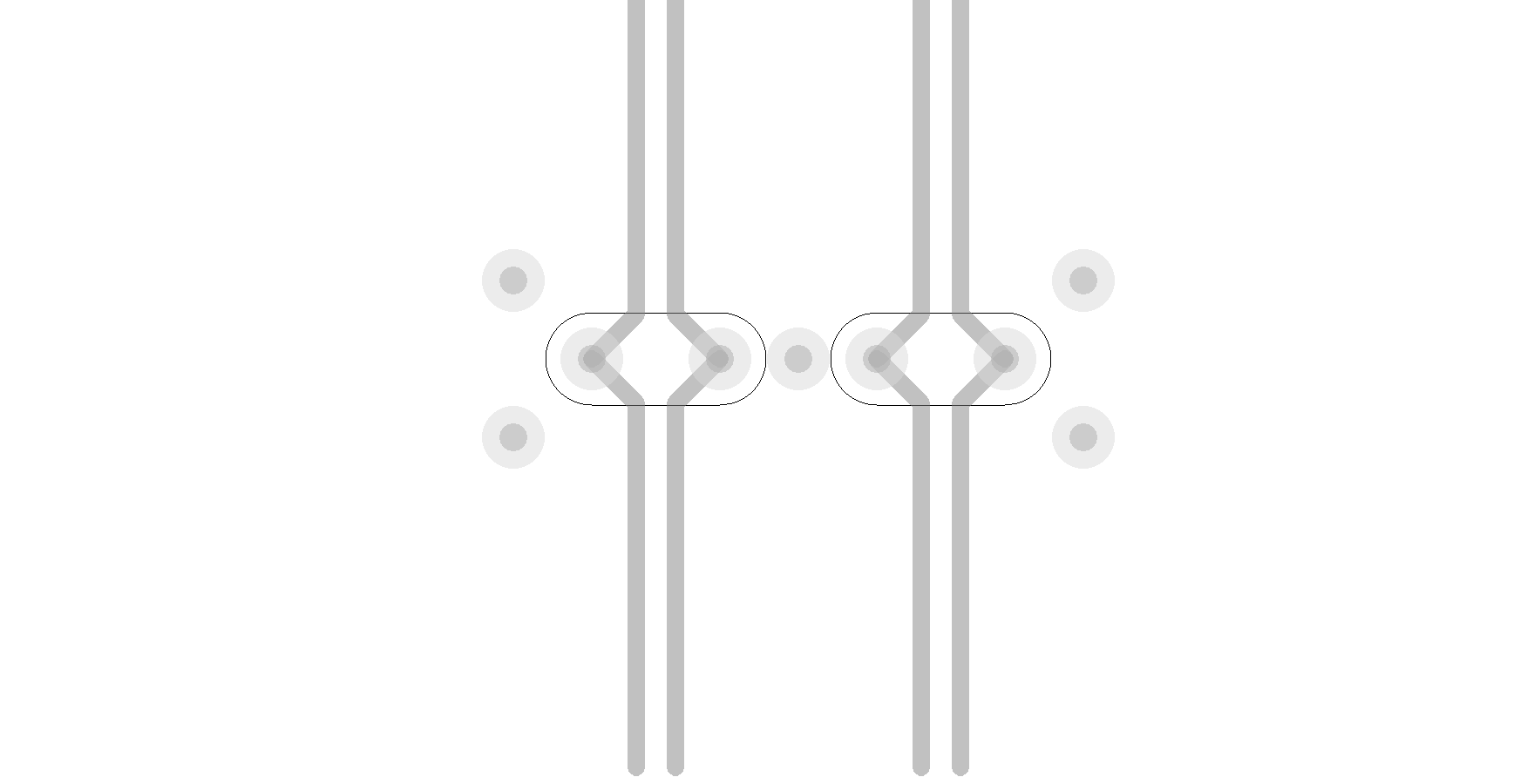
Figure 6. Minimizing crosstalk using shielding half-wire.
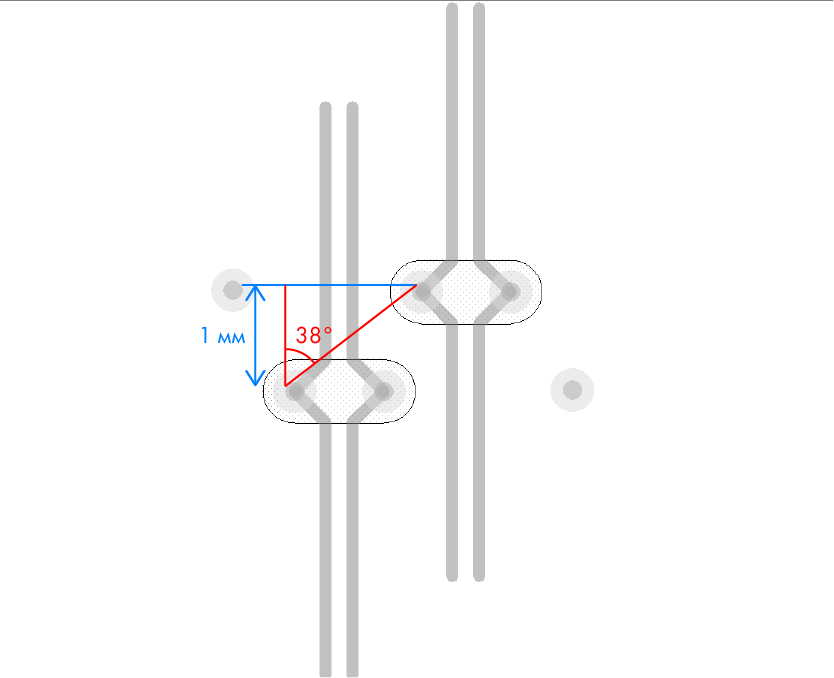
Figure 7. Minimizing crosstalk using a diagonal “checkerboard” shift.
Crosstalk can also be reduced by exotic methods, for example, by a long stub (due to the displacement of the inductive-capacitive balance p / o) [5]. Also, interference can be reduced at the stage of designing the microcircuit case [6].
In addition to adjacent signal circuits, interference from internal layers can affect signal quality.
High currents can flow through the food test sites. Due to the increase in inductance at the edges of the polygons, the flowing currents form edge fields (English Fringing fields) along all the boundaries of the polygon, including cutouts. Edge fields are a source of electromagnetic radiation (born Edge-fired emission) into space. To reduce the emission of electromagnetic radiation, the rule 20H is applied (Figure 8), which consists in narrowing the power supply area in relation to the land area.
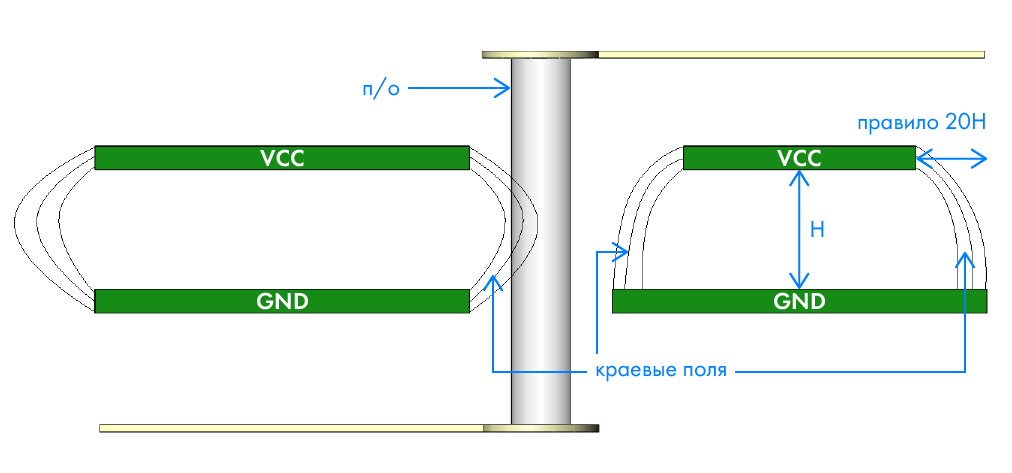
Figure 8. Edge fields and the 20H rule.
To protect the p / o from interference, if possible, it is necessary to increase the antipad at the food ranges. The 20H rule for p / o is difficult to provide, and unnecessarily, an anti-fall diameter of about 2 mm is usually recommended (Figure 9).

Figure 9. Increased anti-drop on food layers
Based on knowledge about the influence of p / o elements on impedance, we can design our ideal p / o. A great start would be calculating the impedance in the calculator. PCB design
engineers like calculators like the Saturn PCB Design Toolkit and the Polar Instruments Si9000e . Both of them allow you to quickly calculate the impedance of a single p / o.
The result obtained in these calculators is very different from each other. This is due to the fact that these tools have a different approach.
Polar calculates the impedance in a two-dimensional plane, where the power supply line crosses the power range. The calculation formula is not given. It was experimentally established that the calculation is made according to the impedance formula of the coaxial cable:

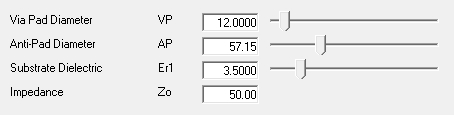
Figure 10. Image from polarinstruments.com
The illustration shows a fairly low value of the dielectric constant Er1, compared with the standard. This is due to the heterogeneity of the dielectric structure: it consists of resin (Er 3.2) and fiberglass filaments (Er 6.1), and therefore has an average dielectric constant of about 4.1. This value can vary quite locally. So, resin prevails near the subsurface, therefore, the dielectric constant is recalculated downward [7].
Saturn PCB calculates the impedance by the formula:
When the p / o length changes, the inductance and capacitance values change disproportionately, the impedance changes. Impedance of exactly the same p / o length 1.6 mm, Saturn PCB calculates as 128 Ohm! (Figure 11)

Figure 11. Calculation of software in the Saturn PCB Design Toolkit.
The question immediately arises: who to believe?
We simulate in a three-dimensional solver of electromagnetic fields (English 3D Solver) how it will look on a real 8-layer board 1.6 mm thick (Figure 12)
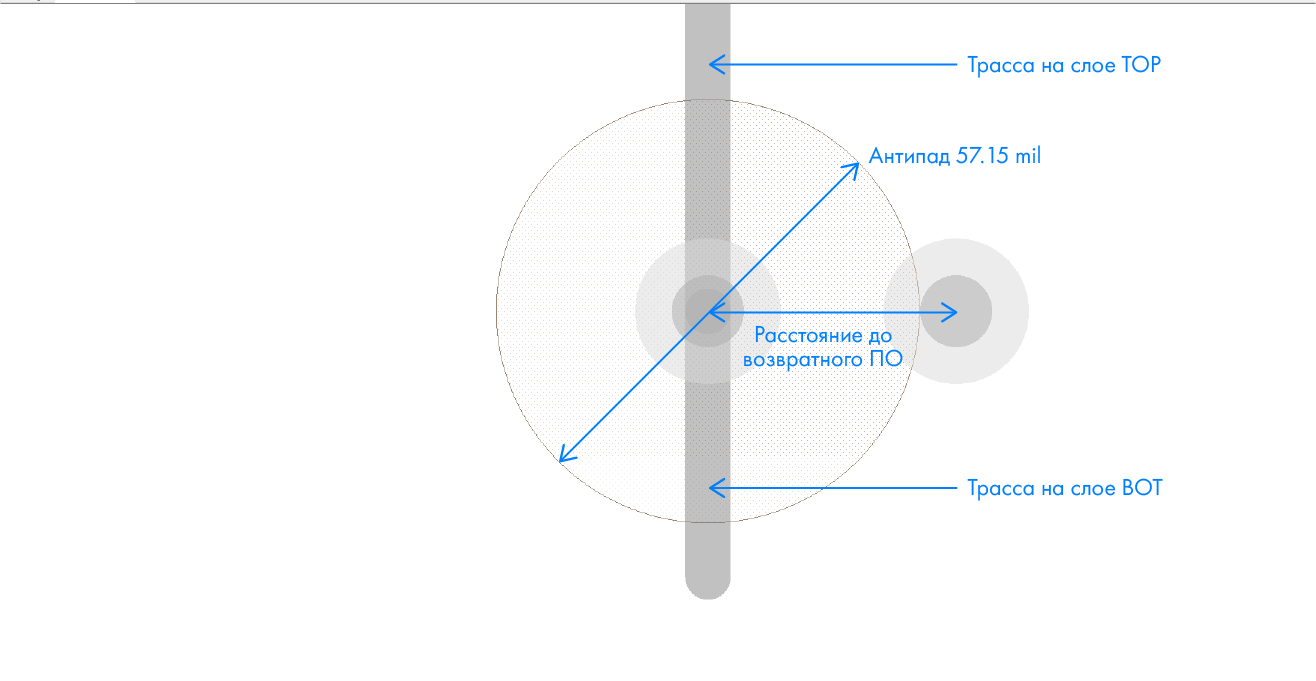
Figure 12. Structure of the transition between layers with a hole for the return current.
In our case, the impedance is about 70 ohms. By approximating the return p / o, you can achieve a decrease of another 5 ohms. Having “played” with the size of the antipad, you can quite accurately adjust the impedance to the target value (Figure 13).
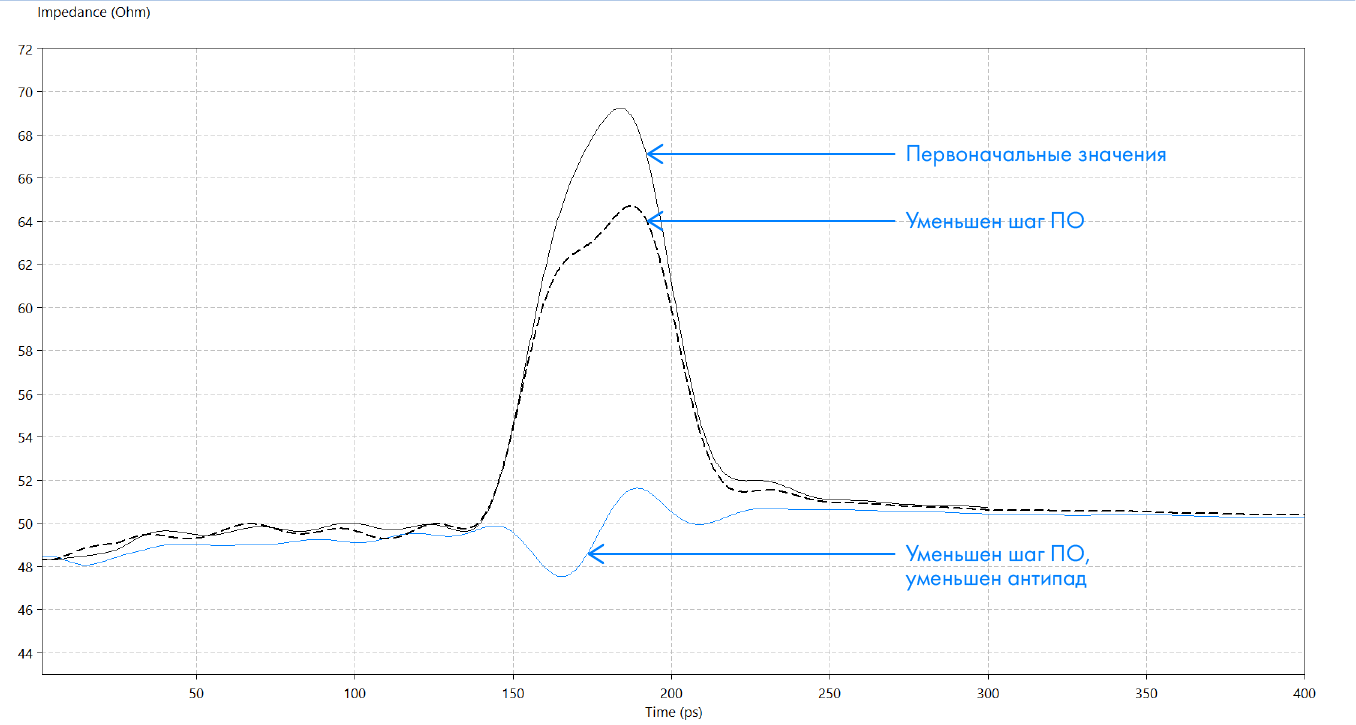
Figure 13. The impedance of the circuit with half-voltage on the time diagram.
In the frequency domain, the “best” parameters are expressed in a lower reflection coefficient from the input (Figure 14).
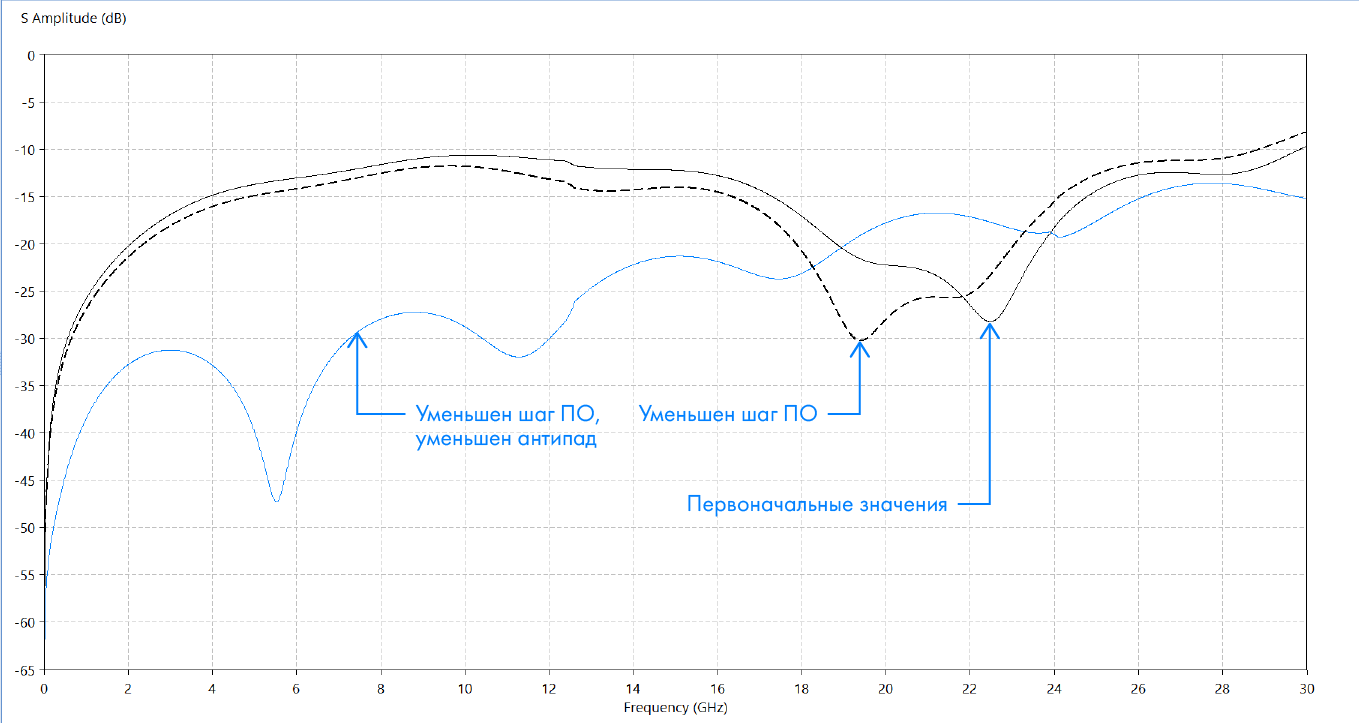
Figure 14. Parameters of single p / o in the frequency domain.
Calculation Polar was closer to the result. Perhaps in order to get an adequate result in the Saturn PCB, corrections are required. If anyone has a positive experience calculating impedance in Saturn, share in the comments!
The calculation of differential p / o is similar to single, except that now we do not have a calculator: the above tools do not consider differential p / o. Also, now we can additionally change the p / o step in the differential. couple.
Take the same structure: an 8-layer board 1.6 mm thick. Consider 9 configurations n / a (Figure 15).
The first 3 p / o have gaps of 0.125 mm and differ only in the location of the holes for the return current. All p / o with 4 onwards have a pitch of 1 mm. P / o from 6 onwards have an increased anti-drop (0.250 mm) and are distinguished by the indentation of the holes for the return current.
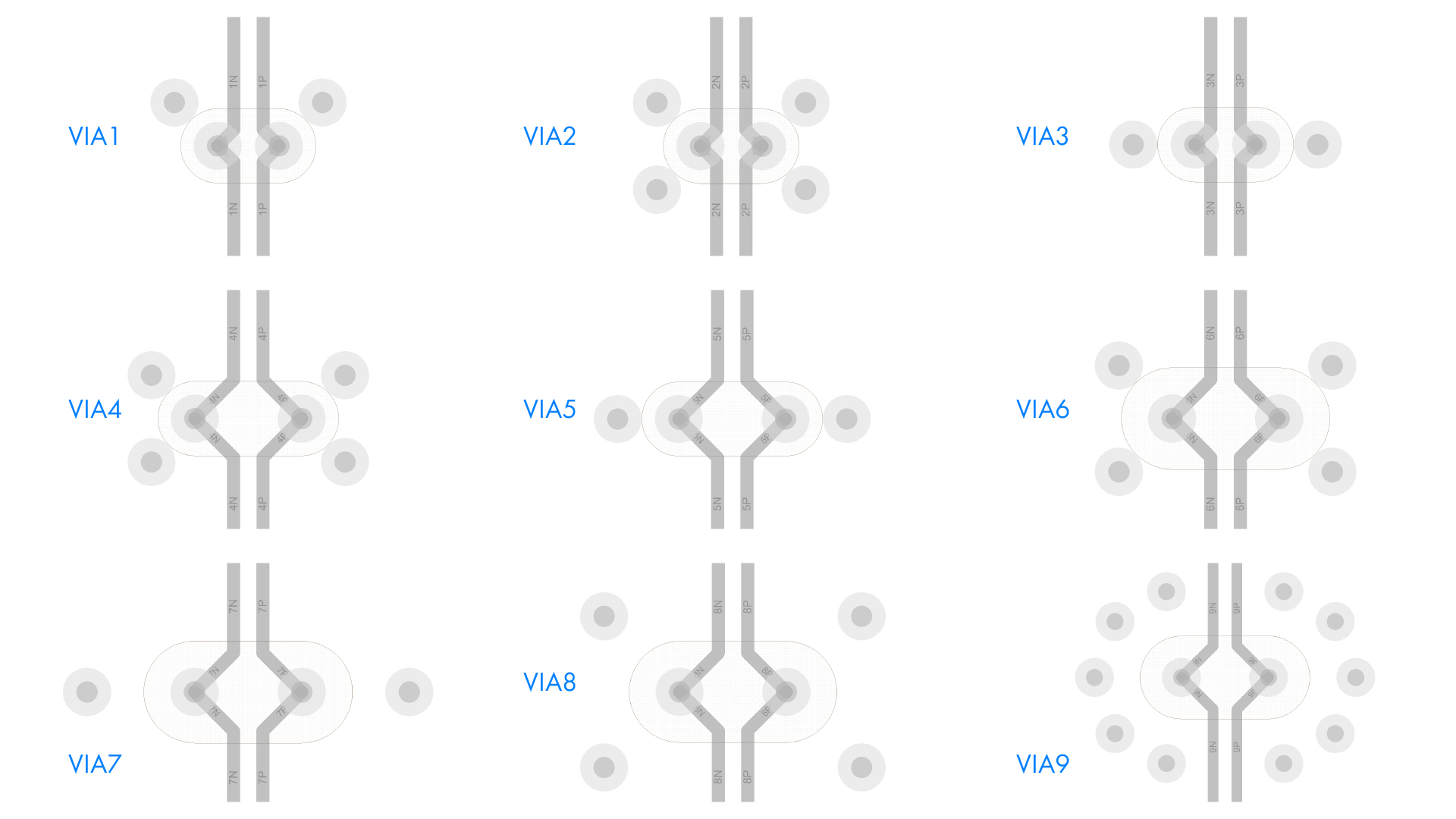
Figure 15. vias.
Consider the impedance plot (Figure 16).

Figure 16. Impedance p / o in the time domain.
On the graph, the “hump" is clearly visible, which corresponds to the vertical section of the half-shell - the "glass" (English Via barrel).
Having examined the frequency dependence of the reflection coefficient VIA1-3 (Figure 17), we see that despite good performance at the target frequency of 6 GHz, there is resonance at lower frequencies. It is preferable to improve via7-9, and if it does not work out, then via4-5 to reduce the "hump" due to the shift of the graphs to the right.

Figure 17. Reflection coefficient from the input p / o.
Reduce the anti-drop in VIA9 to get 0.125 mm gaps. For VIA4, we reduce the p / o step to 0.75 mm and consider the result obtained (Figure 18).

Figure 18. Comparison of the impedance of the modified p / o.
In the frequency domain, a shift of the reflection coefficient graph from the input to the right is visible (Figure 19).

Figure 19. Comparison of the reflection coefficient of the modified software.
Vias in printed circuit boards is a complex and heterogeneous structure. For the correct calculation of the parameters, expensive 3D solvers, competencies and a significant investment of time are necessary.
If it is not possible to avoid the use of transitions of critical signals to other layers, it is necessary first of all to assess the degree of influence of the arising inhomogeneities on the integrity of the signals. If the heterogeneity is electrically short (the delay time is less than 1/6 of the front), the stub resonates at frequencies outside the passband - there is no point in wasting time and money on optimization.
In a first approximation, it is convenient to use ready-made structures from datasheets or previous boards, but remember the features of the current project.
Calculators allow you to quickly evaluate the parameters of software, but they use highly simplified models that negatively affect the result.

Hello everyone, my name is Vyacheslav. I have been developing printed circuit boards for 5 years, and during this time I not only read a lot of rules and recommendations for tracing, but also found the sources and worked with them.
In the complex computing systems that he is developingYADRO company, high-speed signals on the way from the transmitter to the receiver cover significant distances, passing through several boards and making a dozen interlayer transitions. Under such conditions, each carelessly designed vias will make a small contribution to signal degradation, and as a result, the interface may not work.
Signal Integrity
Vias (hereinafter p / o, English via) are heterogeneities in the transmission line. Like other heterogeneities, they spoil the signal. This effect is weakly expressed at low frequencies, but increases significantly with increasing frequency. Often, developers undeservedly pay little attention to the structure of vias: they can be copied from a "neighboring" project, taken from a datasheet, or not specified at all in CAD (the default setting).
Before using the calculated structure, it is necessary to understand why it was made just like that? Blind repetition can only do harm.
The integrity of the signal in the channel when passing through vias is mainly affected by the following factors:
- signal reflection due to changes in wave impedance;
- signal degradation due to stray capacitance and inductance;
- reflections from an unused stretch of semi-plastic during the transition to the inner layer (hereinafter referred to as stub from English via stub);
- crosstalk (English Cross talks);
- interference in power buses.
Let us consider in more detail the causes of these effects and methods for their elimination.
Factor 1. Wave impedance p / o
In an ideally designed board, the wave impedance does not change throughout the route, including when switching to another layer. In reality, it usually looks something like this:

Figure 1. Change in wave impedance upon transition to another layer.
The better the wave resistances are matched, the less will be the reflection of the signal. How to influence this?
Consider the structure of p / o on the board [1].

Figure 2. Structure p / o on the board.
| Layer | Element | Property |
|---|---|---|
| TOP | Playground | Spurious capacitance between the platform and the L2 power range |
| TOP-L2 | n / a cut | Inductance |
| L2 (food testing ground) | Antipad | The antipad forms an edge tank - the capacitance between the walls of the p / o and the feeding ground |
| L2-L3 | N / a | Inductance |
| L3 (food testing ground) | Antipad | The antipad forms an edge tank - the capacitance between the walls of the p / o and the feeding ground |
| L3-L4 | N / a | Inductance |
| L4 (signal) | Playground | Spurious capacitance between the n / a platform and the L3 power range |
| L4-L5 | Headquarters | Noise source |
By changing the p / o elements, we change the wave resistance of the transition. Our goal is to match the impedance of the transition structure with the impedance of conductors to minimize reflections. Let us consider how the impedance changes when the elements of the p / o structure change.
| Element | Act | Electrical property | Impedance (result) |
|---|---|---|---|
| Playground | ↓ | C ↓ | ↑ |
| Diameter p / o | ↓ | L ↑ | ↑ |
| Antipad | ↑ | C ↓ | ↑ |
| Length p / o | ↑ | L ↑ | ↑ |
| The number of food landfills on the way p / o | ↓ | C ↓ | ↑ |
| N / a step | ↑ | C ↓ | ↑ |
| Distance to return p / o | ↑ | L ↑ | ↑ |
| The number of return p / o | ↑ | L ↓ | ↓ |
| Hole filling | Fill with resin (Dk ↑) | C ↑ | ↓ |
Factor 2. Spurious inductance and capacitance
Conductors on a printed circuit board can be made with a wave resistance lying in a wide range, but most often it is 50 Ohms. On the one hand, this is due to historical continuity: the 50 Ohm impedance was standardized for coaxial cables as a compromise between the driver load level and the signal energy loss. On the other hand, a 50-Ohm conductor is easy to fabricate on a standard board.
For the developer, it is important not so much the specific value of the wave resistance as its constancy throughout the entire transmission line.
In order to make a transmission line with a fixed value of wave impedance, the developer selects the width of the track and the distance to the reference layer, i.e. changes the linear capacity and inductance of the transmission line to a certain value.
In p / o, the inductive component is quite significant. In a first approximation, we must, within a reasonable framework, minimize the stray inductance as much as possible, and then change the p / o parameters to achieve a given capacitance, and therefore impedance.
An excessive decrease in the capacitance of a half-wave will cause a local increase in impedance and, as a consequence, signal reflections.
Factor 3. Via stub
What happens when a signal passes through a stub through hole?

Figure 3. Transition hole with stub, resonance at ¼ wavelength.
In our example, the signal propagates from top to bottom from the Top layer. Having reached the inner signal layer, the signal is separated: part moves along the path on the inner layer, and part continues to move down the vias, then it is reflected from the Bottom layer. After the reflected signal has reached the inner layer, it is again divided, part moves along the path, and part returns to the source.
The reflected signal will be summed with the original and distort it, which will be expressed in narrowing the window on the eye diagram, and increasing the level of insertion loss (Eng. Insertion Loss).
In the worst case, the TD segment will be equal to ¼ of the wavelength of the signal, then the reflected signal will reach the path on the inner layer with a delay of half the period, overlapping the original signal in antiphase.
When analyzing the integrity, it is recommended to consider the bandwidth with a width of 5 Nyquist frequencies. A good approximation would be considered acceptable stub, giving a resonance at 7 harmonics and above [2].

Figure 4. Graph of the level of insertion loss for p / o with stubs 0, 0.65, 1.2 mm.
Figure 4 shows a huge resonance at frequencies around 24 GHz. We can conclude that if our signal operates at a frequency of 2-3 GHz, we can afford not to eliminate the stub, because within 7 harmonics “everything is calm”.
You can make a quick assessment of the criticality of the stub in the Polar calculator.:


Figure 5. Image from polarinstruments.com . A stub length of 2.5 mm is acceptable for signals with rise times of more than 500 ps.
The formulas given in the article [2] give a slightly more accurate result. They take into account p / o geometry and allow calculating the correction for the dielectric constant of the dielectric along the Z axis.
You can remove the stub using the “backdrilling” operation (English Backdrilling), or using micro-transitions (English blind and buried vias). The choice depends on the features of the project. Reverse drilling is easier and cheaper. After manufacturing the board, with a larger diameter drill, the stub is drilled to a predetermined depth. The developer is required to specify additional indentation of the topology in the drilling zone, and it is also available for the manufacturer to indicate the drilling requirements in the design documentation. Modern CAD systems support this functionality.
Micro-junctions are primarily intended for high-density boards (English HDI), however, in some cases they can be used by leveling the high cost of refusing to drill back and reducing the number of layers on the board. When developing HDI boards, there are a few things to keep in mind:
- each new type of payroll increases the cost of the board;
- For laser drilling, special optimized prepregs are used, the properties of which may vary;
- metallization of blind holes increases the thickness of copper on the inner layers.
It is highly recommended that the board structure be agreed with the manufacturer in advance.
Factor 4. Crosstalk
Crosstalk - unwanted signal transmission from one line to the next. This transfer occurs because two closely spaced conductors have capacitive and inductive coupling.
The nature of the crosstalk of signal conductors and p / o is slightly different.
The signal does not have a reference layer in the n / a, the return currents flow along the adjacent n / a, forming a large loop. Crosstalk of signals in the n / a due to the inductive component.
The greatest effect on minimizing crosstalk can be achieved by increasing the distance between p / o. However, often the topologist does not have much space.
The convergence of p / o in the differential pair not only reduces the occupied area, but also has a positive effect on noise immunity [3].
A common way to minimize crosstalk between adjacent signal p / o is to place a shielding p / o between them. With this method, it will be necessary to conduct signals in increments of about 2 mm (Figure 6). If there is not enough space, you can use a smaller step with a shift (English Staggered pattern), as in Figure 7. Using simulation, you can choose the ideal angle of shift [4].

Figure 6. Minimizing crosstalk using shielding half-wire.

Figure 7. Minimizing crosstalk using a diagonal “checkerboard” shift.
Crosstalk can also be reduced by exotic methods, for example, by a long stub (due to the displacement of the inductive-capacitive balance p / o) [5]. Also, interference can be reduced at the stage of designing the microcircuit case [6].
Factor 5. Power Bus Interference
In addition to adjacent signal circuits, interference from internal layers can affect signal quality.
High currents can flow through the food test sites. Due to the increase in inductance at the edges of the polygons, the flowing currents form edge fields (English Fringing fields) along all the boundaries of the polygon, including cutouts. Edge fields are a source of electromagnetic radiation (born Edge-fired emission) into space. To reduce the emission of electromagnetic radiation, the rule 20H is applied (Figure 8), which consists in narrowing the power supply area in relation to the land area.

Figure 8. Edge fields and the 20H rule.
To protect the p / o from interference, if possible, it is necessary to increase the antipad at the food ranges. The 20H rule for p / o is difficult to provide, and unnecessarily, an anti-fall diameter of about 2 mm is usually recommended (Figure 9).

Figure 9. Increased anti-drop on food layers
Single vias impedance calculation
Based on knowledge about the influence of p / o elements on impedance, we can design our ideal p / o. A great start would be calculating the impedance in the calculator. PCB design
engineers like calculators like the Saturn PCB Design Toolkit and the Polar Instruments Si9000e . Both of them allow you to quickly calculate the impedance of a single p / o.
The result obtained in these calculators is very different from each other. This is due to the fact that these tools have a different approach.
Polar calculates the impedance in a two-dimensional plane, where the power supply line crosses the power range. The calculation formula is not given. It was experimentally established that the calculation is made according to the impedance formula of the coaxial cable:


Figure 10. Image from polarinstruments.com
The illustration shows a fairly low value of the dielectric constant Er1, compared with the standard. This is due to the heterogeneity of the dielectric structure: it consists of resin (Er 3.2) and fiberglass filaments (Er 6.1), and therefore has an average dielectric constant of about 4.1. This value can vary quite locally. So, resin prevails near the subsurface, therefore, the dielectric constant is recalculated downward [7].
Saturn PCB calculates the impedance by the formula:
When the p / o length changes, the inductance and capacitance values change disproportionately, the impedance changes. Impedance of exactly the same p / o length 1.6 mm, Saturn PCB calculates as 128 Ohm! (Figure 11)

Figure 11. Calculation of software in the Saturn PCB Design Toolkit.
The question immediately arises: who to believe?
We simulate in a three-dimensional solver of electromagnetic fields (English 3D Solver) how it will look on a real 8-layer board 1.6 mm thick (Figure 12)

Figure 12. Structure of the transition between layers with a hole for the return current.
In our case, the impedance is about 70 ohms. By approximating the return p / o, you can achieve a decrease of another 5 ohms. Having “played” with the size of the antipad, you can quite accurately adjust the impedance to the target value (Figure 13).

Figure 13. The impedance of the circuit with half-voltage on the time diagram.
In the frequency domain, the “best” parameters are expressed in a lower reflection coefficient from the input (Figure 14).

Figure 14. Parameters of single p / o in the frequency domain.
Calculation Polar was closer to the result. Perhaps in order to get an adequate result in the Saturn PCB, corrections are required. If anyone has a positive experience calculating impedance in Saturn, share in the comments!
Differential vias impedance calculation
The calculation of differential p / o is similar to single, except that now we do not have a calculator: the above tools do not consider differential p / o. Also, now we can additionally change the p / o step in the differential. couple.
Take the same structure: an 8-layer board 1.6 mm thick. Consider 9 configurations n / a (Figure 15).
The first 3 p / o have gaps of 0.125 mm and differ only in the location of the holes for the return current. All p / o with 4 onwards have a pitch of 1 mm. P / o from 6 onwards have an increased anti-drop (0.250 mm) and are distinguished by the indentation of the holes for the return current.

Figure 15. vias.
Consider the impedance plot (Figure 16).

Figure 16. Impedance p / o in the time domain.
On the graph, the “hump" is clearly visible, which corresponds to the vertical section of the half-shell - the "glass" (English Via barrel).
Having examined the frequency dependence of the reflection coefficient VIA1-3 (Figure 17), we see that despite good performance at the target frequency of 6 GHz, there is resonance at lower frequencies. It is preferable to improve via7-9, and if it does not work out, then via4-5 to reduce the "hump" due to the shift of the graphs to the right.

Figure 17. Reflection coefficient from the input p / o.
Reduce the anti-drop in VIA9 to get 0.125 mm gaps. For VIA4, we reduce the p / o step to 0.75 mm and consider the result obtained (Figure 18).

Figure 18. Comparison of the impedance of the modified p / o.
In the frequency domain, a shift of the reflection coefficient graph from the input to the right is visible (Figure 19).

Figure 19. Comparison of the reflection coefficient of the modified software.
Final recommendations
Vias in printed circuit boards is a complex and heterogeneous structure. For the correct calculation of the parameters, expensive 3D solvers, competencies and a significant investment of time are necessary.
If it is not possible to avoid the use of transitions of critical signals to other layers, it is necessary first of all to assess the degree of influence of the arising inhomogeneities on the integrity of the signals. If the heterogeneity is electrically short (the delay time is less than 1/6 of the front), the stub resonates at frequencies outside the passband - there is no point in wasting time and money on optimization.
In a first approximation, it is convenient to use ready-made structures from datasheets or previous boards, but remember the features of the current project.
Calculators allow you to quickly evaluate the parameters of software, but they use highly simplified models that negatively affect the result.
List of references
- Chin, T. Differential pairs: four things you need to know about vias. Retrieved from TI E2E Community: https://e2e.ti.com/blogs_/b/analogwire/archive/2015/06/10/differential-pairs-four-things-you-need-to-know-about-vias#
- Simonovich, B. Via Stubs Demystified. Retrieved from Bert Simonovich's Design Notes: https://blog.lamsimenterprises.com/2017/03/08/via-stubs-demystified/
- Demystifying Vias in High-Speed PCB Design. Retrieved from Keysight Technology: https://www.keysight.com
- K. Aihara, J. Buan, A. Nagao, T. Takada and C.C. Huang, “Minimizing differential crosstalk of vias for high-speed data transmission,” in Proc. 14th Elect. Perform. Electron. Packages and Systems, Portland, OR, Oct. 2014.
- C.M. Nieh and J. Park, “Far-end Crosstalk Cancellation using Via Stub for DDR4 Memory Channel,” in Proc. 63rd Electronics Components and Technology Conference, Las Vegas, NV, May 2013, pp. 2035-2040.
- H. Kanno, H. Ogura and K. Takahashi, “Surface-mountable Liquid Crystal Polymer Package with Vertical Via Transition Compensating Wire Inductance up to V-band,” in IEEE MTT-S Int. Microwave Symp. Dig., Philadelphia, PA, June 2003, pp. 1159-1162.
- Via Pad / Anti-Pad Impedance Calculation. Retrieved from Polar instruments https://www.polarinstruments.com/support/si/AP8178.html
