Unity: an endless procedurally generated city obtained using the WFC algorithm (wave function collapse)
- Transfer
Hello, Habr!
As trendsetters on the theme Unity in the Russian market, we offer you to read an interesting study on the practical use of WFC algorithm (Wave Function Collapse), built in the image of the well-known principle of quantum mechanics and is very convenient for procedural generation levels in the game. Earlier on Habré the detailed story about this algorithm was already published . The author of today's article, Marian Kleineberg, considers the algorithm in the context of three-dimensional graphics and the generation of an endless city. Enjoy reading!

We’ll talk about a game where you walk through an endless city that is procedurally generated as you move. A city is built from a set of blocks using the WFC algorithm (wave function collapse).
The playable assembly is available for download on the itch.io website . You can also take the source code on github . Finally, I propose a video in which I walk through the city thus generated.
I will call the word “cell” a 3D voxel mesh element that can contain a block or be empty. The word "module" I will call a block that can occupy such a cell.
The algorithm decides which modules to select in each cell of the game world. An array of cells is considered a wave function in an unobservable form. Thus, each cell corresponds to many modules that may appear in it. In terms of quantum mechanics, one could say, "the cell is in a superposition of all modules." The existence of the world begins in a completely unobservable form, where any module can be in each cell. Further, all cells collapse, one after another. This means that for each cell one module is randomly selected from all possible.
The next step is constraint propagation. For each module, a subset of modules is selected that are allowed to be adjacent to it. Each time a module collapses, subsets of other modules are updated, which are still allowed as adjacent to it. The stage of propagation of restrictions is the most resource-consuming part of the algorithm in terms of computing power.
An important aspect of the algorithm is determining which cell to collapse. The algorithm always collapses the cell with the smallest entropy. This is a cell that allows a minimal number of choices (that is, a cell with the least randomness). If the probability of collapse is the same for all modules, then the cell with the minimum number of possible modules will have the lowest entropy. As a rule, the probabilities of being selected are different for the various modules available. A cell with two possible modules having the same probability provides a wider choice (greater entropy) than the one in which there are two modules, and for one of them the probability of falling under the choice is very high, and for the other it is very small.

(Gif posted by ExUtumno on Github)
More detailed information about the wave function collapse algorithm, as well as a number of beautiful examples, can be found here. Initially, this algorithm was proposed for generating 2D textures based on a single sample. In this case, the probabilistic indicators of the modules and adjacency rules are determined depending on their occurrence in the example. This article provides this information manually.
Here is a video demonstrating this algorithm in action.
The world is generated from a set in which about 100 blocks. I created them using Blender. At first, I had very few blocks, and I added them little by little when I considered it necessary.

The algorithm needs to know which modules can be located next to each other. For each module, there are 6 lists of possible neighbors, one in each of the directions. However, I wanted to avoid having to create such a list manually. In addition, I wanted to automatically generate rotated options for each of my blocks.
Both of these tasks are solved using the so-called prototype modules. In essence, this is
A complex problem arose with modeling adjacency information, so that this automatic process worked. Here's what I got:

Each block has 6 contacts, one for each face. The contact has a number. In addition, the horizontal contacts may be inverted, not inverted, or symmetrical. Vertical contacts either have a rotation index in the range from 0 to 3, or are marked as rotationally invariant .
Based on this, I can automatically check which modules are allowed to fit together. Adjoining modules must have the same pin numbers. Their symmetry must also coincide (the same vertical rotation index, a pair of inverted and non-inverted horizontal contacts), or the modules must be symmetric / invariant.
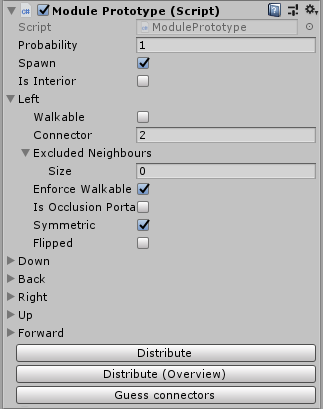
There are exclusion rules by which I can prohibit neighborhood options that would be allowed by default. Some blocks with matching contacts simply look ugly nearby. Here is an example of a map generated without applying exception rules:

The original wave function collapse algorithm generates finite-size maps. I wanted to build a world that will expand and expand as you move along it.
At first I tried to generate fragments of finite size and use the contacts of adjacent fragments as restrictions. If a fragment is generated, and a fragment adjacent to it is also generated, then only such modules are allowed that fit next to existing modules. With this approach, the following problem arises: whenever a cell collapses, the propagation of restrictions will cut down opportunities even at a distance of several cells. The following image shows the effects of collapsing a single cell:

If at each step of the algorithm only one fragment is generated, then the restrictions do not apply to adjacent fragments. In this case, such modules were selected inside the fragment that would be unacceptable if other fragments are taken into account. As a result, when the algorithm tried to generate the next fragment, it could not find a single solution.
Now I no longer use fragments, but store the map in a dictionary that displays the position of a cell on a cell. The cell is filled only if necessary. Some elements of the algorithm should be adjusted with this in mind. When choosing a cell that should collapse, it is impossible to take into account all cells if their number is infinite. Instead, we only generate a small portion of the map at a time, once the player reaches it. Outside this area, restrictions continue to spread.
In some cases, this approach does not work. Consider a set of modules for a straight section of a tunnel from the figure above - there is no entrance to the tunnel. If the algorithm chooses such a tunnel module, then the tunnel will be infinite by definition. At the stage of distribution of restrictions, the program will try to select an infinite number of cells. I developed a special set of modules to get around this problem.
There are two important boundary conditions. All faces on the top level of the map must have “air” contacts. All faces on the base of the map must have “solid” contacts. If these conditions are not met, then on the map there will be holes in the ground, and some buildings will be without a roof.
On a map of finite size, this problem would be easily solved. For all cells at the highest and lowest level, it would be necessary to remove all modules with inappropriate contacts. Then start the distribution of restrictions and remove the remaining modules that no longer suit us.
On a map of infinite size, this will not work, because both at the highest and at the lowest level, we have an infinite number of cells. The most naive solution is to delete all inappropriate cells immediately as they arise. However, when a module is removed at the upper level, restrictions apply to those cells that are adjacent to it. There is an avalanche effect, again leading to an infinite selection of cells.
I solved this problem by creating a 1 × n × 1 map, where n is the height. This map uses world wrapping to spread restrictions. The mechanism works as in the game Pacman: going beyond the right edge of the map, the character returns to it because of the left edge. Now I can apply any restrictions to my map. Each time you create a new cell on an infinite map, this cell is initialized with a set of modules corresponding to a specific position on the map.
Sometimes the WFC algorithm reaches a state in which the cell does not correspond to any possible module. In applications where we are dealing with a world of finite size, you can simply reset the result and start all over again. In an infinite world, this will not work, as part of the world is already shown to the player. First, I settled on a solution in which the places where the errors occurred were filled with white blocks.
I am currently using return search. The order of the collapse of the cells and some information about the distribution of restrictions is stored in the form of history. If the WFC algorithm fails, then part of the history is canceled. As a rule, this works, but sometimes errors can be recognized too late, and a return search covers a lot of steps. In rare cases, the cell in which the player is located is regenerated.
In my opinion, due to this limitation, the application of the WFC algorithm with infinite worlds is not suitable for commercial games.
I started working on this task after I watched Oscar Stelberg's lecture on how he uses the algorithm to generate levels in the game Bad North. In general, my algorithm was implemented during the week of procjam .
I have some ideas for further refinement of this algorithm, but I’m not sure that someday I’m going to add gameplay to it. And if I get together - for sure it will not be such an epic strategy that you already imagined. However, if you want to check how your favorite game mechanics works with this algorithm - just try it yourself! In the end, the source code is publicly available and licensed by MIT.
As trendsetters on the theme Unity in the Russian market, we offer you to read an interesting study on the practical use of WFC algorithm (Wave Function Collapse), built in the image of the well-known principle of quantum mechanics and is very convenient for procedural generation levels in the game. Earlier on Habré the detailed story about this algorithm was already published . The author of today's article, Marian Kleineberg, considers the algorithm in the context of three-dimensional graphics and the generation of an endless city. Enjoy reading!

We’ll talk about a game where you walk through an endless city that is procedurally generated as you move. A city is built from a set of blocks using the WFC algorithm (wave function collapse).
The playable assembly is available for download on the itch.io website . You can also take the source code on github . Finally, I propose a video in which I walk through the city thus generated.
Algorithm
I will call the word “cell” a 3D voxel mesh element that can contain a block or be empty. The word "module" I will call a block that can occupy such a cell.
The algorithm decides which modules to select in each cell of the game world. An array of cells is considered a wave function in an unobservable form. Thus, each cell corresponds to many modules that may appear in it. In terms of quantum mechanics, one could say, "the cell is in a superposition of all modules." The existence of the world begins in a completely unobservable form, where any module can be in each cell. Further, all cells collapse, one after another. This means that for each cell one module is randomly selected from all possible.
The next step is constraint propagation. For each module, a subset of modules is selected that are allowed to be adjacent to it. Each time a module collapses, subsets of other modules are updated, which are still allowed as adjacent to it. The stage of propagation of restrictions is the most resource-consuming part of the algorithm in terms of computing power.
An important aspect of the algorithm is determining which cell to collapse. The algorithm always collapses the cell with the smallest entropy. This is a cell that allows a minimal number of choices (that is, a cell with the least randomness). If the probability of collapse is the same for all modules, then the cell with the minimum number of possible modules will have the lowest entropy. As a rule, the probabilities of being selected are different for the various modules available. A cell with two possible modules having the same probability provides a wider choice (greater entropy) than the one in which there are two modules, and for one of them the probability of falling under the choice is very high, and for the other it is very small.

(Gif posted by ExUtumno on Github)
More detailed information about the wave function collapse algorithm, as well as a number of beautiful examples, can be found here. Initially, this algorithm was proposed for generating 2D textures based on a single sample. In this case, the probabilistic indicators of the modules and adjacency rules are determined depending on their occurrence in the example. This article provides this information manually.
Here is a video demonstrating this algorithm in action.
About blocks, prototypes and modules
The world is generated from a set in which about 100 blocks. I created them using Blender. At first, I had very few blocks, and I added them little by little when I considered it necessary.

The algorithm needs to know which modules can be located next to each other. For each module, there are 6 lists of possible neighbors, one in each of the directions. However, I wanted to avoid having to create such a list manually. In addition, I wanted to automatically generate rotated options for each of my blocks.
Both of these tasks are solved using the so-called prototype modules. In essence, this is
MonoBehaviourconvenient to work with in the Unity editor. Modules along with lists of valid neighboring elements and rotated options are automatically created based on such prototypes.A complex problem arose with modeling adjacency information, so that this automatic process worked. Here's what I got:

Each block has 6 contacts, one for each face. The contact has a number. In addition, the horizontal contacts may be inverted, not inverted, or symmetrical. Vertical contacts either have a rotation index in the range from 0 to 3, or are marked as rotationally invariant .
Based on this, I can automatically check which modules are allowed to fit together. Adjoining modules must have the same pin numbers. Their symmetry must also coincide (the same vertical rotation index, a pair of inverted and non-inverted horizontal contacts), or the modules must be symmetric / invariant.

There are exclusion rules by which I can prohibit neighborhood options that would be allowed by default. Some blocks with matching contacts simply look ugly nearby. Here is an example of a map generated without applying exception rules:

Way to infinity
The original wave function collapse algorithm generates finite-size maps. I wanted to build a world that will expand and expand as you move along it.
At first I tried to generate fragments of finite size and use the contacts of adjacent fragments as restrictions. If a fragment is generated, and a fragment adjacent to it is also generated, then only such modules are allowed that fit next to existing modules. With this approach, the following problem arises: whenever a cell collapses, the propagation of restrictions will cut down opportunities even at a distance of several cells. The following image shows the effects of collapsing a single cell:

If at each step of the algorithm only one fragment is generated, then the restrictions do not apply to adjacent fragments. In this case, such modules were selected inside the fragment that would be unacceptable if other fragments are taken into account. As a result, when the algorithm tried to generate the next fragment, it could not find a single solution.
Now I no longer use fragments, but store the map in a dictionary that displays the position of a cell on a cell. The cell is filled only if necessary. Some elements of the algorithm should be adjusted with this in mind. When choosing a cell that should collapse, it is impossible to take into account all cells if their number is infinite. Instead, we only generate a small portion of the map at a time, once the player reaches it. Outside this area, restrictions continue to spread.
In some cases, this approach does not work. Consider a set of modules for a straight section of a tunnel from the figure above - there is no entrance to the tunnel. If the algorithm chooses such a tunnel module, then the tunnel will be infinite by definition. At the stage of distribution of restrictions, the program will try to select an infinite number of cells. I developed a special set of modules to get around this problem.
Border conditions
There are two important boundary conditions. All faces on the top level of the map must have “air” contacts. All faces on the base of the map must have “solid” contacts. If these conditions are not met, then on the map there will be holes in the ground, and some buildings will be without a roof.
On a map of finite size, this problem would be easily solved. For all cells at the highest and lowest level, it would be necessary to remove all modules with inappropriate contacts. Then start the distribution of restrictions and remove the remaining modules that no longer suit us.
On a map of infinite size, this will not work, because both at the highest and at the lowest level, we have an infinite number of cells. The most naive solution is to delete all inappropriate cells immediately as they arise. However, when a module is removed at the upper level, restrictions apply to those cells that are adjacent to it. There is an avalanche effect, again leading to an infinite selection of cells.
I solved this problem by creating a 1 × n × 1 map, where n is the height. This map uses world wrapping to spread restrictions. The mechanism works as in the game Pacman: going beyond the right edge of the map, the character returns to it because of the left edge. Now I can apply any restrictions to my map. Each time you create a new cell on an infinite map, this cell is initialized with a set of modules corresponding to a specific position on the map.
Error conditions and return search
Sometimes the WFC algorithm reaches a state in which the cell does not correspond to any possible module. In applications where we are dealing with a world of finite size, you can simply reset the result and start all over again. In an infinite world, this will not work, as part of the world is already shown to the player. First, I settled on a solution in which the places where the errors occurred were filled with white blocks.
I am currently using return search. The order of the collapse of the cells and some information about the distribution of restrictions is stored in the form of history. If the WFC algorithm fails, then part of the history is canceled. As a rule, this works, but sometimes errors can be recognized too late, and a return search covers a lot of steps. In rare cases, the cell in which the player is located is regenerated.
In my opinion, due to this limitation, the application of the WFC algorithm with infinite worlds is not suitable for commercial games.
Background
I started working on this task after I watched Oscar Stelberg's lecture on how he uses the algorithm to generate levels in the game Bad North. In general, my algorithm was implemented during the week of procjam .
I have some ideas for further refinement of this algorithm, but I’m not sure that someday I’m going to add gameplay to it. And if I get together - for sure it will not be such an epic strategy that you already imagined. However, if you want to check how your favorite game mechanics works with this algorithm - just try it yourself! In the end, the source code is publicly available and licensed by MIT.
