Complex systems. Reaching a critical level
- Transfer
If you spent some time thinking about complex systems, you probably understand the importance of networks. Networks rule our world. From chemical reactions inside the cell, to the network of relationships in the ecosystem, to the trading and political networks that shape the course of history.
Or consider this article you are reading. You probably found it on a social network , downloaded it from a computer network and are currently deciphering the meaning using your neural network .
But no matter how much I thought about networks over the years, until recently, I did not understand the importance of simple diffusion .
This is our topic for today: how, how randomly everything moves and spreads. Some examples to warm your appetite:
Brief remark about the form.
Unlike all my previous works, this essay is interactive [the original article contains interactive examples with sliders and buttons that control objects on the screen - approx. lane].
So let's get started. The first task is to develop a visual dictionary for distribution across networks.
I am sure that you all know the basis of networks, that is, nodes + edges. To investigate diffusion, it is only necessary to mark some nodes as active . Or, as epidemiologists infected like to say :

This activation or infection spreads over the network from node to node in accordance with the rules that we will develop below.
Real networks are usually much larger than this simple network of seven nodes. They are also much more confusing. But for simplicity, we will build a toy model here to study the lattice, that is, the lattice network.
(The fact that the grid lacks realism is compensated by the fact that it is easy to draw;)
Unless otherwise indicated, there are four neighbors in the network nodes, for example:
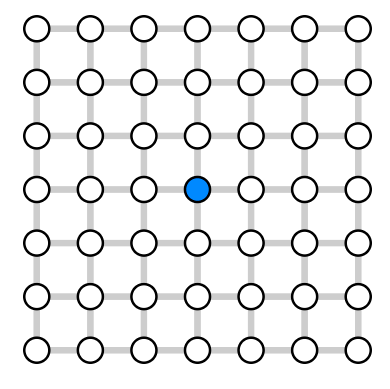
And you need to imagine that these gratings extend endlessly in all directions. In other words, we are not interested in behavior that occurs only at the edges of the network or in small populations.
Given that the grids are so ordered, you can simplify them to pixels. For example, these two images represent the same network:

In one of the behaviors, the active node always passes the infection to its (uninfected) neighbors. But it's boring. Much more interesting things happen when transmission is probabilistic .
In the SIR (Susceptible-Infected-Removed) model, a node can be in three states:
Here's how the interactive simulation works [in the original article, you can choose the infection transmission rate from 0 to 1, see the process step by step or in full - approx. trans.]:
In the context of the disease, removal may mean that the person has died or that he has developed immunity to the pathogen. We say that they are “removed” from the simulation because nothing else happens to them.
Depending on what we are trying to model, you may need a different model than the SIR.
If we simulate the spread of measles or an outbreak of a forest fire, SIR is perfect. But suppose we simulate the spread of new cultural practices, such as meditation. At first, the node (person) is susceptible because it has never done it before. Then, if he begins to meditate (perhaps after hearing about it from a friend), we will model him as infected. But if he stops practicing, he will not die and will not fall out of the simulation, because in the future he can easily adopt this habit again. So he goes back into a susceptible state.
This is a SIS model.(Susceptible – Infected – Susceptible). The classic model has two parameters: transfer rate and recovery rate. However, in the simulations for this article, I decided to simplify it by lowering the recovery speed parameter. Instead, the infected node automatically returns to the susceptible state in the next time step, unless it is infected by one of its neighbors. In addition, we allow the node infected in step n to infect itself in step n + 1 with a probability equal to the transmission speed.
As you can see, this is very different from the SIR model.
Since the nodes are never removed, even a very small and limited lattice can support SIS infection for a long time. Infection simply jumps from node to node and returns.
Despite the differences, SIR and SIS are surprisingly fungible for our purposes. Therefore, for the rest of the article, we will focus on SIS - mainly because it is more tenacious and, therefore, it is more interesting to work with it.
Having played with the SIR and SIS models, you might notice something about the longevity of the infection. At very low transmission rates, such as 10%, the infection tends to die out. While at higher values such as 50%, the infection remains alive and captures most of the network. If the network were infinite, we could imagine that it continues and spreads forever.
Such unlimited diffusion has many names: “viral”, “nuclear” or (in the title of this article) critical .
It turns out that there is a specific turning point that separates subcritical networks (doomed to extinction) from supercritical networks (capable of infinite growth). This tipping point is calledcritical threshold , and this is a fairly common sign of diffusion processes in conventional networks.
The exact value of the critical threshold varies between networks. What is common is the presence of such a meaning.
[In the interactive demo from the original article, you can try to manually find the critical threshold of the network by changing the value of the transmission speed. It is somewhere between 22% and 23% - approx. per.]
At 22% (and lower), the infection eventually dies. At 23% (and higher), the initial infection sometimes dies, but in most cases it manages to survive and spread long enough to ensure its eternal existence.
(By the way, there is a whole scientific field devoted to the search for these critical thresholds for different network topologies. For a quick introduction, I recommend quickly scrolling through the Wikipedia article on the flow threshold ).
In general, here's how it works: below a critical threshold, any final infection in the network is guaranteed (with probability 1) to die out eventually. But above the critical threshold there is a probability (p> 0) that the infection will last forever, and at the same time spread arbitrarily far from the original place.
However, note that a supercritical network does not guarantee that the infection will last forever. In fact, it often fades, especially in the very early stages of modeling. Let's see how this happens.
Suppose we started with one infected node and four neighbors. In the first step of modeling, the infection has 5 independent chances of spreading (including the chance to “spread” to itself in the next step):
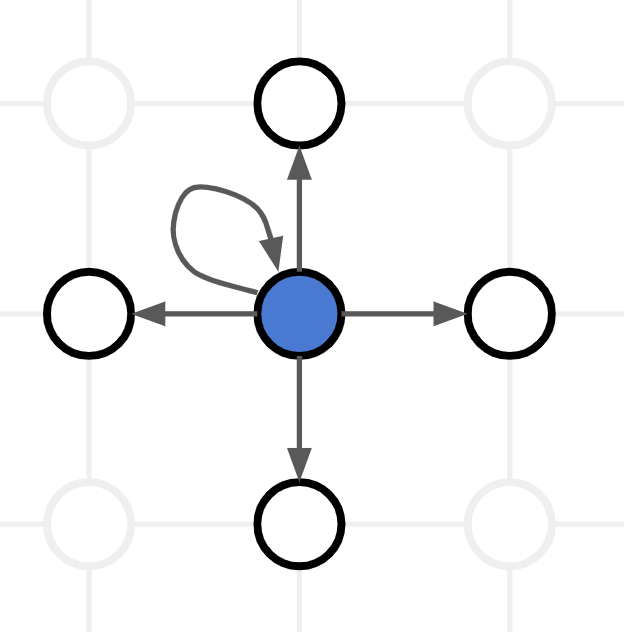
Now suppose the transmission rate is 50%. In this case, in the first step, we throw a coin five times. And if five eagles fall, the infection will be destroyed. This happens in about 3% of cases - and this is only the first step. An infection that has survived the first step has some (usually less) chance to fade in the second step, some (even less) chance to fade in the third step, etc.
Thus, even when the network is supercritical - if the transmission rate is 99% - there is a chance that the infection will disappear.
But the important thing is that she is not alwayswill fade away. If we add up the probability of attenuation of all steps to infinity, the result is less than 1. In other words, with a non-zero probability, the infection will continue forever. This is what it means for a network to be supercritical.
Up to this point, all our simulations began with a small piece of pre-infected nodes in the center.
But what if you start from scratch? Then we simulate spontaneous activation - the process by which a susceptible node becomes infected accidentally (not from one of its neighbors).
This is called the SISa model . The letter “a” means “automatic”.
A new parameter appears in the SISa simulation - the rate of spontaneous activation, which changes the frequency of occurrence of spontaneous infection (the transmission rate parameter, which we saw earlier, is also present).
What does an infection need to spread throughout the network?
You may have noticed in the simulation that increasing the speed of spontaneous activation does not change whether the infection captures the entire network or not. Only the transmission rate determines whether the network is pre- or supercritical. And when the network is subcritical (transmission rate less than or equal to 22%), no infection can spread to the entire lattice, no matter how often it starts.
It's like starting a fire in a wet field. You can set fire to a few dry leaves, but the flame goes out quickly, because the rest of the landscape is not easily ignited (subcritical). While in a very dry field (supercritical) one spark is enough to start a raging fire.
Similar things are observed in the field of ideas and inventions. Often the world is not ready for the idea, and in this case it can be invented again and again, but it does not cling to the masses. On the other hand, the world can be completely ready for invention (large hidden demand), and as soon as it is born, it is accepted by everyone. In the middle are ideas that are invented in several places and distributed locally, but not enough for a particular version to cover the entire network at once. In this last category we find, for example, agriculture and writing, which were independently invented by different human civilizations about ten and three times, respectively.
Suppose we make some nodes completely invulnerable, i.e. immune to activation. It is as if they were initially in a remote state, and the SIS (a) model runs on the remaining nodes.
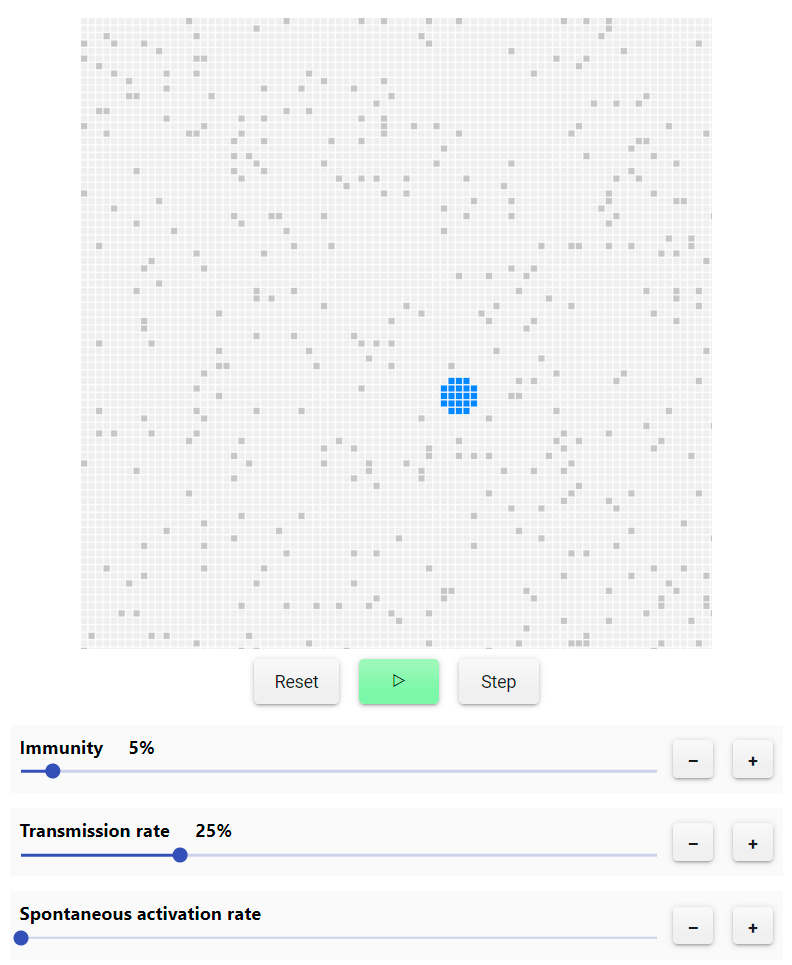
The immunity slider controls the percentage of remote nodes. Try changing its value (while the model is running!) And see how it affects the state of the network whether it will be supercritical or not.
Changing the number of immune nodes completely changes the picture; there will be a network of pre- or supercritical. And it’s easy to understand why. With a large number of immune hosts, the infection has fewer opportunities for spreading to new hosts.
It turns out that this entails a number of very important practical consequences.
One of them is preventing the spread of forest fires. At the local level, each person should take their own precautions (for example, never leave an open flame unattended). But on a large scale, individual outbreaks are inevitable. Thus, another method of protection is to ensure a sufficient number of “gaps” (in a network of flammable materials) so that the flash does not cover the entire network. Such a function is performed by glades:

Another outbreak that is important to stop is an infectious disease. This introduces the concept of population immunity . This is the idea that some people cannot be vaccinated (for example, they have a compromised immune system), but if enough people are immune to the infection, the disease cannot spread indefinitely. In other words, a sufficient portion of the population should be vaccinated to transfer the population from a supercritical to a subcritical state. When this happens, one patient can still become infected (for example, after traveling to another region), but without a supercritical network in which to grow, the disease will infect only a handful of people.
Finally, the concept of refractory nodes explains what happens in a nuclear reactor. In a chain reaction, a decaying uranium-235 atom releases about three neutrons, which cause (on average) the fission of more than one U-235 atom. New neutrons then cause further atomic fission and so on exponentially:

When creating a bomb, the whole point is to ensure unhindered continuation of exponential growth. But at a power plant, the goal is to generate energy without killing everyone around. To do this, control rods are used , made of a material capable of absorbing neutrons (for example, silver or boron). Since they absorb rather than release neutrons, in our simulation they act as immune units, thereby preventing the reactor core from entering a supercritical state.
Thus, the trick of a nuclear reactor is to keep the reaction near a critical threshold by moving the control rods back and forth, and to ensure that whenever something goes wrong, the rods sink into the core and stop it.
The degree of a node is the number of its neighbors. Up to this point, we have been considering 4th degree networks. But what happens if you change this setting?
For example, you can connect each node not only with four immediate neighbors, but also with four diagonally. In such a network, the degree will be 8.

Lattices with degrees 4 and 8 are well symmetrical. But at degree 5 (for example), the problem arises: which five neighbors to choose? In this case, we select the four nearest neighbors (N, E, S, W), and then randomly select one neighbor from the set {NE, SE, SW, NW}. The choice is made independently for each node at each time step.
Again, it is not difficult to understand what is happening here. When each node has more neighbors, then the chances of spreading the infection increase - and, thus, the network is more likely to become critical.
However, the consequences may be unexpected, as we will see below.
Until now, our networks have been completely homogeneous. Each node looks like any other. But what if we change the conditions and allow different states of nodes throughout the network?
For example, try to simulate cities. To do this, increase the density in some parts of the network (a higher degree of nodes). We do this on the basis of data that citizens have a wider social circle and more social interactions than people outside cities.
In our model, susceptible nodes are colored based on their degree. Knots in the “countryside” have degree 4 (and are colored light gray), while nodes in the “cities” have higher degrees (and are darker), starting from degree 5 on the outskirts and ending with 8 in the city center .
Try to choose such a speed of distribution that activation covers cities, and then does not go beyond their borders.
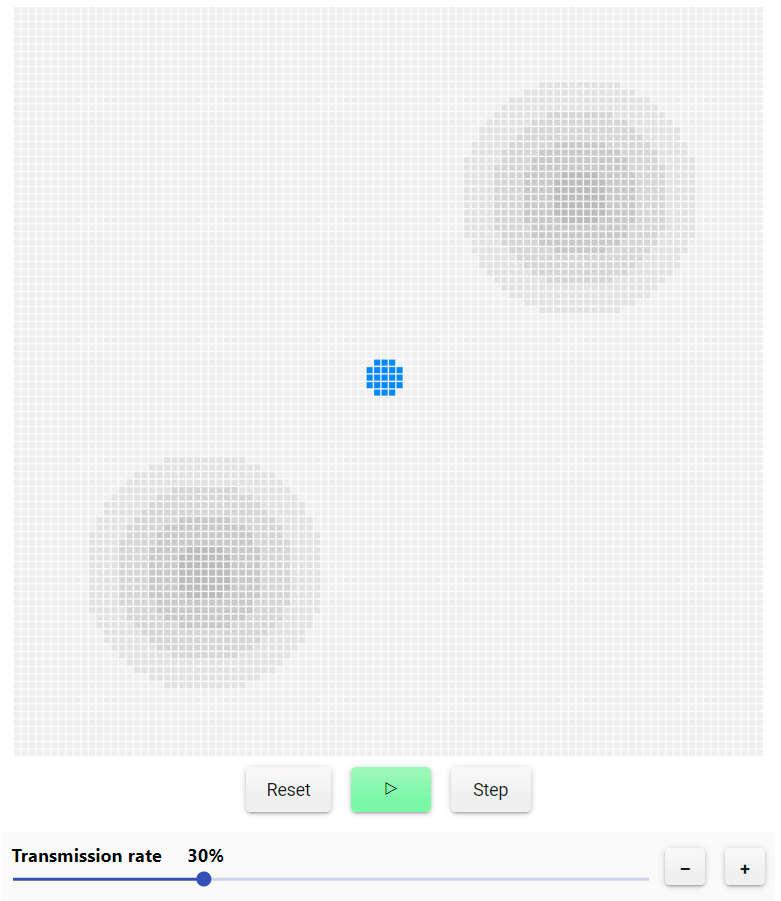
I find this simulation both obvious and amazing. Of course , cities maintain a better cultural level than rural areas - everyone knows that. What surprises me is that part of this cultural diversity arises simply on the basis of the topology of the social network.
This is an interesting point, I will try to explain in more detail.
Here we are dealing with cultural forms that are transmitted simply and directly from person to person. For example, manners , salon games, fashion trends, linguistic trends, rituals of small groups and products that are spread by word of mouth, plus whole packets of information that we call ideas.
(Note: the dissemination of information between people is extremely complicated by the media. It is easier to imagine a kind of technologically primitive environment, for example, Ancient Greece, where almost every spark of culture was transmitted by interaction in the physical space).
From the above simulation, I learned that there are ideas and cultural practices that can be rooted and spread in the city, but they simply are not able to spread in rural areas (mathematically they cannot). These are the same ideas and the same people. It’s not that the villagers are somehow “near”: when interacting with the same idea, they have exactly the same chances to pick it uplike the townspeople. It’s just that the idea itself cannot become viral in the countryside, because there are not many links through which it can spread.
This is perhaps the easiest to see in the field of fashion - clothes, hairstyles, etc. In the fashion network, we can fix the edge of the lattice when two people notice each other's outfits. In the city center, each person can see more than 1000 other people every day - on the street, in the subway, in a crowded restaurant, etc. In the countryside, on the contrary, each person can see only a couple dozen others. Based only on this difference , the city is able to support more fashion trends. And only the most compelling trends - with the highest transmission speed - will be able to gain a foothold outside the city.
We tend to think that if the idea is good, then ultimately it will reach everyone, and if the idea is bad, it will disappear. Of course, this is true in extreme cases, but between them there are a bunch of ideas and practices that can only become viral in certain networks. This is really awesome.
Here we consider the effect of network density . It is defined for a given set of nodes as the number of actual edges divided by the number of potential edges . That is the percentage of possible connections that really exist.
So, we have seen that the density of the network in urban centers is higher than in rural areas. But cities are not the only place where we find dense networks.
An interesting example is high schools. For example, for a particular district, we compare the network that exists among schoolchildren with the network that exists among their parents. The same geographical area and the same population, but one network is many times denser than another. Therefore, it is not surprising that fashion and linguistic trends spread much faster among adolescents.
Similarly, elite networks are usually much denser than non-elite networks - in my opinion, this fact is underestimated (people who are popular or influential spend more time creating networks, and therefore they have more “neighbors” than usual people). Based on the above simulations, we expect that elite networks will support some cultural forms that cannot be supported by the mainstream, simply based on mathematical laws, according to the average degree of the network. I leave you to reflect on what these cultural forms may be.
Finally, we can apply this idea to the Internet, simulating it as huge and very densetown. It is not surprising that many new types of culture thrive on the Internet, which simply cannot be supported on purely spatial networks: niche hobbies, better design standards, greater awareness of injustice, etc. And these are not only pleasant things. Just as the first cities were a hotbed of diseases that could not spread with a low population density, the Internet is also a breeding ground for malignant cultural forms such as clickbait, fake news and incitement of artificial indignation.
We often think of discovery or invention as a process that occurs in the mind of a single genius. He is struck by a flash of inspiration and - eureka! - suddenly we get a new way to measure volume. Or the equation of gravity. Or a light bulb.
But if we take the point of view of a lone inventor at the time of discovery, then we look at the phenomenon from the point of view of the node . While it would be more correct to interpret the invention as a network phenomenon.
Networking is important in at least two ways. Firstly, already existing ideas must penetrate consciousness.inventor. These are quotes from a new article, a bibliographic section of a new book - giants, on whose shoulders stood Newton. Secondly, the network is critical for bringing a new idea back to the world; an invention that has not spread is hardly worth calling an “invention” at all. Thus, for both of these reasons, it makes sense to model the invention - or, in a broad sense, the growth of knowledge - as a diffusion process.
In a moment, I will present a crude simulation of how knowledge within a network can spread and grow. But first I have to explain.
At the beginning of the simulation, there are four experts in each quadrant of the grid, located as follows:
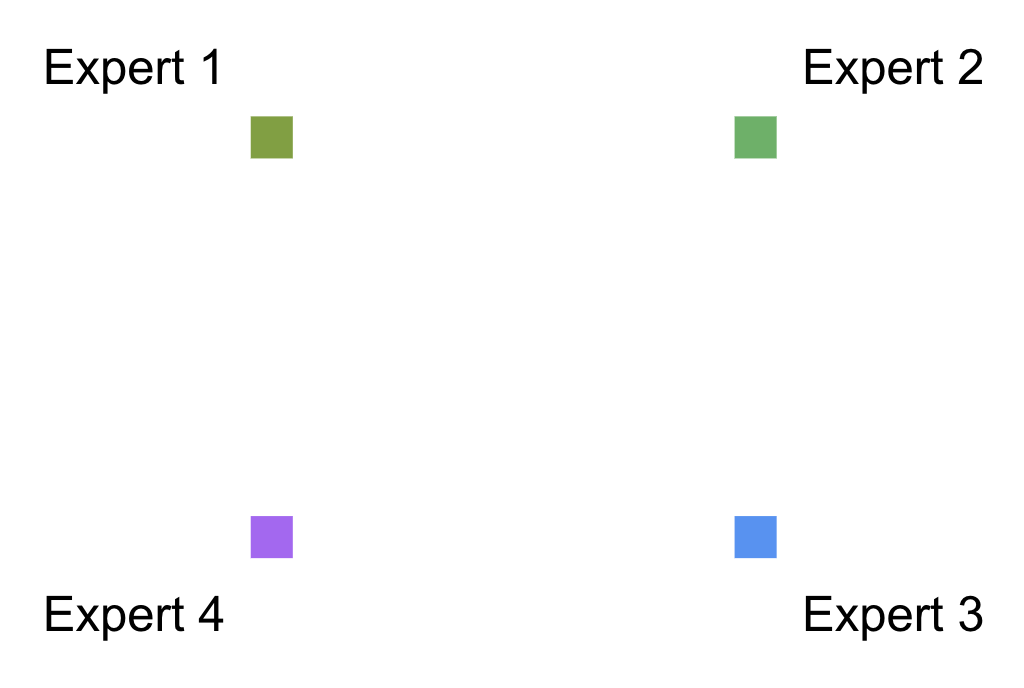
Expert 1 has the first version of the idea - let's call it Idea 1.0. Expert 2 is a person who knows how to turn Idea 1.0 into Idea 2.0. Expert 3 knows how to convert Idea 2.0 to Idea 3.0. And finally, the fourth expert knows how to bring the finishing touches to create Idea 4.0.

This is similar to a technique like origami, where methods are developed and combined with other methods to create more interesting designs. Or it may be a field of knowledge similar to physics, in which later work is based on the fundamental work of predecessors.
The essence of this simulation is that we need all four experts to contribute to the final version of the idea. And at each stage, the idea must be brought to the appropriate expert.

A few reservations. The simulation encoded many unrealistic assumptions. Here are just a few of them:
… and many others.
This is a ridiculously simplified model of how knowledge actually grows. Outside the scope of the model there are a lot of important details (see above). However, it reflects the essential essence of the process. And so we can, with reservations, talk about the growth of knowledge, using our knowledge of diffusion.
In particular, the diffusion model gives an understanding of how to speed up the process : it is necessary to facilitate the exchange of ideas between expert nodes. This may mean cleaning the network of dead nodes that interfere with diffusion. Or it could mean placing all the experts in a city or cluster with high network density, where ideas are spreading fast. Or just put them in one room:

So ... that’s all I can tell about diffusion.
But I have one last thought, and it is very important. It is about the growth ( and stagnation ) of knowledge in scientific communities. This idea is different in tone and content from everything that was said above, but I hope you will forgive me.
The illustration shows one of the most important positive feedback cycles in the world (and it has been like this for quite some time):
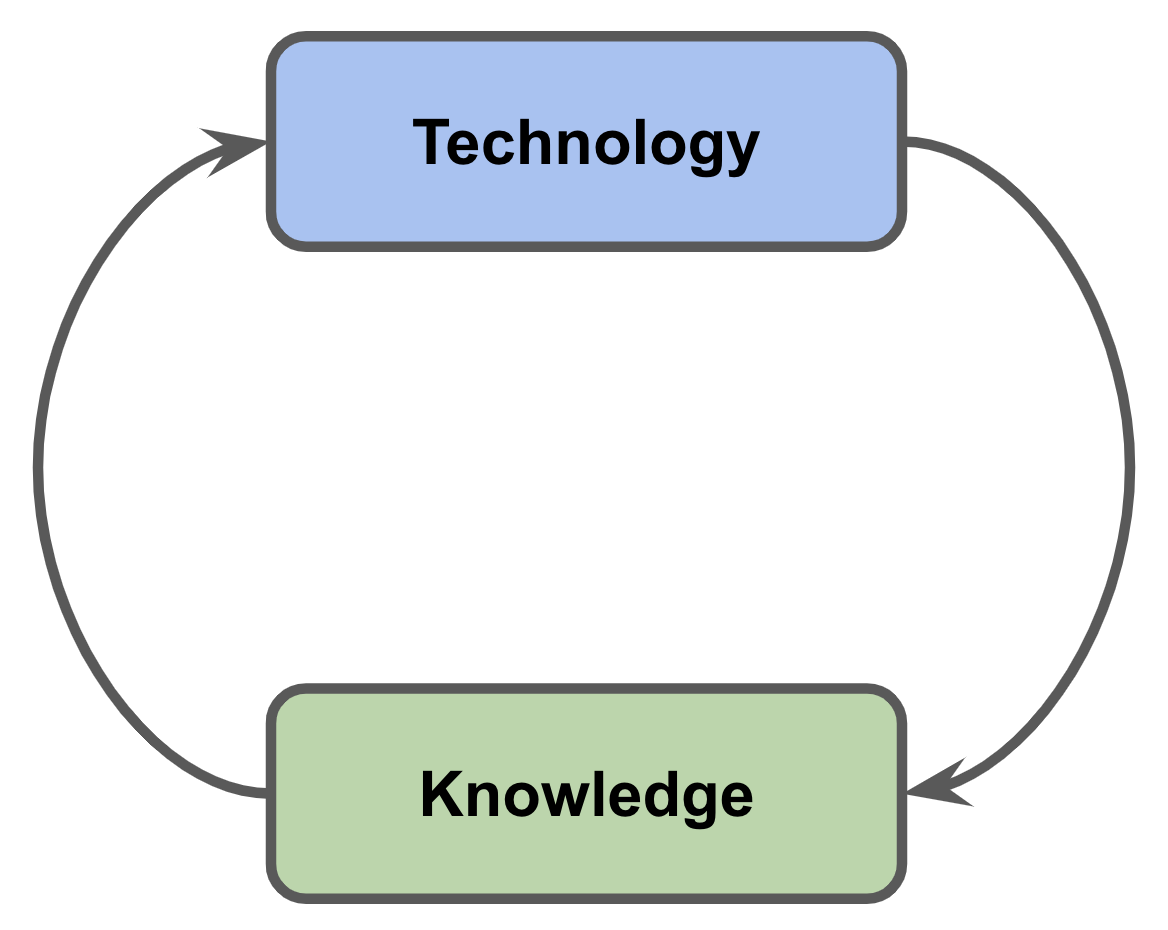
The upstream cycle (K ⟶ T) is quite simple: we use new knowledge to develop new tools. For example, an understanding of the physics of semiconductors allows us to create computers.
However, the downward move requires some explanation. How does technology development lead to increased knowledge?
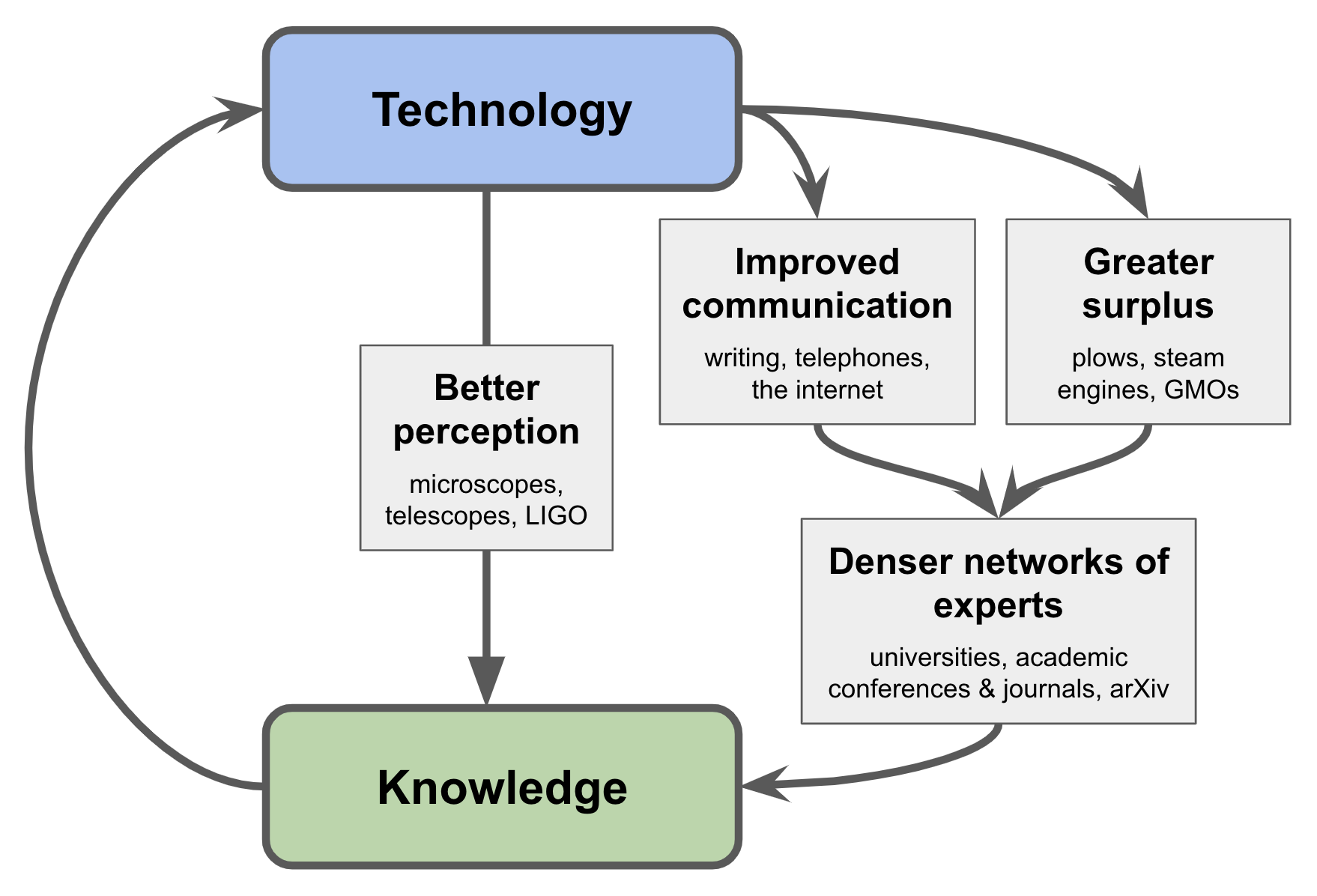
One way - perhaps the most direct - is when new technologies give us new ways of perceiving the world. For example, the best microscopes allow you to look deeper into the cell, throwing ideas for molecular biology. GPS trackers show how animals move. Sonar allows you to explore the oceans. Etc.
Sure, this is a vital mechanism, but there are at least two other ways from technology to knowledge. They may not be so simple, but I think they are just as important:
First one . Technology leads to economic abundance (i.e. wealth), and this allows more people to engage in the production of knowledge.
If 90% of the population of your country is engaged in agriculture, and the remaining 10% are engaged in some form of trade (or war), then people have very little free time to think about the laws of nature. Perhaps that is why in former times, science was promoted mainly by children from wealthy families.
The United States annually graduates more than 50,000 doctors of science. Instead of having a person go to work at the plant at the age of 18 (or earlier), the graduate student has to be financed up to 30 or, possibly, up to 40 years - and even then it is not clear whether his work will bring any real economic effect. But it is necessary for a person to reach the forefront in his discipline, especially in such complex fields as physics or biology.
The fact is that, from the point of view of systems, specialists are expensive. And the ultimate source of social wealth that finances these professionals is new technology: plow subsidizes the pen.
Second. New technologies, especially in the field of travel and communications, are changing the structure of social networks in which knowledge is growing. In particular, this allows experts and specialists to interact more closely with each other.
Notable inventions here include a printing press, steamboats and railways (facilitating travel and / or sending mail over long distances), telephones, airplanes and the Internet. All these technologies contribute to increasing network density, especially within specialized communities (where almost all knowledge growth occurs). For example, correspondence networks that arose among European scientists at the end of the Middle Ages, or how modern physicists use arXiv.
Ultimately, both of these paths are similar. Both increase the density of the network of specialists, which in turn leads to an increase in knowledge:
For many years I have been rather dismissive of higher education. A short stay in graduate school left an unpleasant aftertaste in the mouth. But now, when I look back and think (to ignore all personal problems), I must conclude that higher education is still extremely important.
Academic social networks (for example, research communities) are one of the most advanced and valuable structures created by our civilization. Nowhere have we accumulated a large concentration of specialists focused on the production of knowledge. Nowhere have people developed in themselves a greater ability to understand and criticize each other's ideas. This is the beating heart of progress. It is in these networks that the fire of enlightenment burns the most.
But we cannot take progress for granted. If the crisis with the irreproducibility of experiments has taught us something, it is that science can have systemic problems. This is a kind of network degradation.
Suppose we distinguish two ways of doing science: real science and careerism . Real science is practices that reliably produce knowledge. She is motivated by curiosity and characterized by honesty (Feynman: “You see, I just need to understand the world”). Careerism, in contrast, is motivated by professional ambitions and is characterized by a game of politics and scientific labels. He may look and act like a science, but does not produce reliable knowledge.
(Yes, this is an exaggerated dichotomy. Just a thought experiment. Do not blame me).
The fact is that when careerists occupy a place in the real research community, they spoil the work. They strive to promote themselves, while the rest of the community is trying to gain new knowledge and share it. Instead of striving for clarity, careerists complicate and confuse everything in order to sound more impressive. They do (as Harry Frankfurt would say) scientific bullshit. And, therefore, we could model them as dead nodes, immune to the bona fide exchange of information necessary for the growth of knowledge:

Perhaps the best model is one in which career nodes are not just immune to knowledge, but actively disseminate fake knowledge . Fake knowledge may include insignificant results, the importance of which is artificially inflated, or really false results that arise from manipulation or fabricated data.
Regardless of how we model them, careerists can certainly strangle our scientific communities.
This is similar to the nuclear chain reaction that we desperately need - we need an explosion of knowledge - only in our enriched U-235 is there too much admixture of the non-reactive isotope U-238 that suppresses the chain reaction.
Of course, there is no clear difference between careerists and real scientists. Each of us has a bit of careerism. The question is how long the network can withstand before the spread of knowledge fades.
Oh, you read it to the end. Thank you for reading.
CC0 All Rights Reserved. You can use this work as you see fit :).
Or consider this article you are reading. You probably found it on a social network , downloaded it from a computer network and are currently deciphering the meaning using your neural network .
But no matter how much I thought about networks over the years, until recently, I did not understand the importance of simple diffusion .
This is our topic for today: how, how randomly everything moves and spreads. Some examples to warm your appetite:
- Infectious diseases passing from carrier to carrier within a population.
- Memes spread across the followers graph on social networks.
- Forest fire.
- Ideas and practices that permeate culture.
- Cascade of neutrons in enriched uranium.
Brief remark about the form.
Unlike all my previous works, this essay is interactive [the original article contains interactive examples with sliders and buttons that control objects on the screen - approx. lane].
So let's get started. The first task is to develop a visual dictionary for distribution across networks.
Simple model
I am sure that you all know the basis of networks, that is, nodes + edges. To investigate diffusion, it is only necessary to mark some nodes as active . Or, as epidemiologists infected like to say :

This activation or infection spreads over the network from node to node in accordance with the rules that we will develop below.
Real networks are usually much larger than this simple network of seven nodes. They are also much more confusing. But for simplicity, we will build a toy model here to study the lattice, that is, the lattice network.
(The fact that the grid lacks realism is compensated by the fact that it is easy to draw;)
Unless otherwise indicated, there are four neighbors in the network nodes, for example:

And you need to imagine that these gratings extend endlessly in all directions. In other words, we are not interested in behavior that occurs only at the edges of the network or in small populations.
Given that the grids are so ordered, you can simplify them to pixels. For example, these two images represent the same network:

In one of the behaviors, the active node always passes the infection to its (uninfected) neighbors. But it's boring. Much more interesting things happen when transmission is probabilistic .
SIR and SIS
In the SIR (Susceptible-Infected-Removed) model, a node can be in three states:
- Susceptible
- Infected
- Removed
Here's how the interactive simulation works [in the original article, you can choose the infection transmission rate from 0 to 1, see the process step by step or in full - approx. trans.]:
- Nodes start as susceptible, with the exception of a few nodes that start as infected.
- At each time step, the infected nodes get a chance to transmit the infection to each of their susceptible neighbors with a probability equal to the transmission rate.
- The infected nodes then go to the “deleted” state, that is, they are no longer able to infect others or become infected themselves.
In the context of the disease, removal may mean that the person has died or that he has developed immunity to the pathogen. We say that they are “removed” from the simulation because nothing else happens to them.
Depending on what we are trying to model, you may need a different model than the SIR.
If we simulate the spread of measles or an outbreak of a forest fire, SIR is perfect. But suppose we simulate the spread of new cultural practices, such as meditation. At first, the node (person) is susceptible because it has never done it before. Then, if he begins to meditate (perhaps after hearing about it from a friend), we will model him as infected. But if he stops practicing, he will not die and will not fall out of the simulation, because in the future he can easily adopt this habit again. So he goes back into a susceptible state.
This is a SIS model.(Susceptible – Infected – Susceptible). The classic model has two parameters: transfer rate and recovery rate. However, in the simulations for this article, I decided to simplify it by lowering the recovery speed parameter. Instead, the infected node automatically returns to the susceptible state in the next time step, unless it is infected by one of its neighbors. In addition, we allow the node infected in step n to infect itself in step n + 1 with a probability equal to the transmission speed.
Discussion
As you can see, this is very different from the SIR model.
Since the nodes are never removed, even a very small and limited lattice can support SIS infection for a long time. Infection simply jumps from node to node and returns.
Despite the differences, SIR and SIS are surprisingly fungible for our purposes. Therefore, for the rest of the article, we will focus on SIS - mainly because it is more tenacious and, therefore, it is more interesting to work with it.
Critical level
Having played with the SIR and SIS models, you might notice something about the longevity of the infection. At very low transmission rates, such as 10%, the infection tends to die out. While at higher values such as 50%, the infection remains alive and captures most of the network. If the network were infinite, we could imagine that it continues and spreads forever.
Such unlimited diffusion has many names: “viral”, “nuclear” or (in the title of this article) critical .
It turns out that there is a specific turning point that separates subcritical networks (doomed to extinction) from supercritical networks (capable of infinite growth). This tipping point is calledcritical threshold , and this is a fairly common sign of diffusion processes in conventional networks.
The exact value of the critical threshold varies between networks. What is common is the presence of such a meaning.
[In the interactive demo from the original article, you can try to manually find the critical threshold of the network by changing the value of the transmission speed. It is somewhere between 22% and 23% - approx. per.]
At 22% (and lower), the infection eventually dies. At 23% (and higher), the initial infection sometimes dies, but in most cases it manages to survive and spread long enough to ensure its eternal existence.
(By the way, there is a whole scientific field devoted to the search for these critical thresholds for different network topologies. For a quick introduction, I recommend quickly scrolling through the Wikipedia article on the flow threshold ).
In general, here's how it works: below a critical threshold, any final infection in the network is guaranteed (with probability 1) to die out eventually. But above the critical threshold there is a probability (p> 0) that the infection will last forever, and at the same time spread arbitrarily far from the original place.
However, note that a supercritical network does not guarantee that the infection will last forever. In fact, it often fades, especially in the very early stages of modeling. Let's see how this happens.
Suppose we started with one infected node and four neighbors. In the first step of modeling, the infection has 5 independent chances of spreading (including the chance to “spread” to itself in the next step):

Now suppose the transmission rate is 50%. In this case, in the first step, we throw a coin five times. And if five eagles fall, the infection will be destroyed. This happens in about 3% of cases - and this is only the first step. An infection that has survived the first step has some (usually less) chance to fade in the second step, some (even less) chance to fade in the third step, etc.
Thus, even when the network is supercritical - if the transmission rate is 99% - there is a chance that the infection will disappear.
But the important thing is that she is not alwayswill fade away. If we add up the probability of attenuation of all steps to infinity, the result is less than 1. In other words, with a non-zero probability, the infection will continue forever. This is what it means for a network to be supercritical.
SISa: spontaneous activation
Up to this point, all our simulations began with a small piece of pre-infected nodes in the center.
But what if you start from scratch? Then we simulate spontaneous activation - the process by which a susceptible node becomes infected accidentally (not from one of its neighbors).
This is called the SISa model . The letter “a” means “automatic”.
A new parameter appears in the SISa simulation - the rate of spontaneous activation, which changes the frequency of occurrence of spontaneous infection (the transmission rate parameter, which we saw earlier, is also present).
What does an infection need to spread throughout the network?
Discussion
You may have noticed in the simulation that increasing the speed of spontaneous activation does not change whether the infection captures the entire network or not. Only the transmission rate determines whether the network is pre- or supercritical. And when the network is subcritical (transmission rate less than or equal to 22%), no infection can spread to the entire lattice, no matter how often it starts.
It's like starting a fire in a wet field. You can set fire to a few dry leaves, but the flame goes out quickly, because the rest of the landscape is not easily ignited (subcritical). While in a very dry field (supercritical) one spark is enough to start a raging fire.
Similar things are observed in the field of ideas and inventions. Often the world is not ready for the idea, and in this case it can be invented again and again, but it does not cling to the masses. On the other hand, the world can be completely ready for invention (large hidden demand), and as soon as it is born, it is accepted by everyone. In the middle are ideas that are invented in several places and distributed locally, but not enough for a particular version to cover the entire network at once. In this last category we find, for example, agriculture and writing, which were independently invented by different human civilizations about ten and three times, respectively.
Immunity
Suppose we make some nodes completely invulnerable, i.e. immune to activation. It is as if they were initially in a remote state, and the SIS (a) model runs on the remaining nodes.

The immunity slider controls the percentage of remote nodes. Try changing its value (while the model is running!) And see how it affects the state of the network whether it will be supercritical or not.
Discussion
Changing the number of immune nodes completely changes the picture; there will be a network of pre- or supercritical. And it’s easy to understand why. With a large number of immune hosts, the infection has fewer opportunities for spreading to new hosts.
It turns out that this entails a number of very important practical consequences.
One of them is preventing the spread of forest fires. At the local level, each person should take their own precautions (for example, never leave an open flame unattended). But on a large scale, individual outbreaks are inevitable. Thus, another method of protection is to ensure a sufficient number of “gaps” (in a network of flammable materials) so that the flash does not cover the entire network. Such a function is performed by glades:

Another outbreak that is important to stop is an infectious disease. This introduces the concept of population immunity . This is the idea that some people cannot be vaccinated (for example, they have a compromised immune system), but if enough people are immune to the infection, the disease cannot spread indefinitely. In other words, a sufficient portion of the population should be vaccinated to transfer the population from a supercritical to a subcritical state. When this happens, one patient can still become infected (for example, after traveling to another region), but without a supercritical network in which to grow, the disease will infect only a handful of people.
Finally, the concept of refractory nodes explains what happens in a nuclear reactor. In a chain reaction, a decaying uranium-235 atom releases about three neutrons, which cause (on average) the fission of more than one U-235 atom. New neutrons then cause further atomic fission and so on exponentially:

When creating a bomb, the whole point is to ensure unhindered continuation of exponential growth. But at a power plant, the goal is to generate energy without killing everyone around. To do this, control rods are used , made of a material capable of absorbing neutrons (for example, silver or boron). Since they absorb rather than release neutrons, in our simulation they act as immune units, thereby preventing the reactor core from entering a supercritical state.
Thus, the trick of a nuclear reactor is to keep the reaction near a critical threshold by moving the control rods back and forth, and to ensure that whenever something goes wrong, the rods sink into the core and stop it.
Power
The degree of a node is the number of its neighbors. Up to this point, we have been considering 4th degree networks. But what happens if you change this setting?
For example, you can connect each node not only with four immediate neighbors, but also with four diagonally. In such a network, the degree will be 8.

Lattices with degrees 4 and 8 are well symmetrical. But at degree 5 (for example), the problem arises: which five neighbors to choose? In this case, we select the four nearest neighbors (N, E, S, W), and then randomly select one neighbor from the set {NE, SE, SW, NW}. The choice is made independently for each node at each time step.
Discussion
Again, it is not difficult to understand what is happening here. When each node has more neighbors, then the chances of spreading the infection increase - and, thus, the network is more likely to become critical.
However, the consequences may be unexpected, as we will see below.
Cities and network density
Until now, our networks have been completely homogeneous. Each node looks like any other. But what if we change the conditions and allow different states of nodes throughout the network?
For example, try to simulate cities. To do this, increase the density in some parts of the network (a higher degree of nodes). We do this on the basis of data that citizens have a wider social circle and more social interactions than people outside cities.
In our model, susceptible nodes are colored based on their degree. Knots in the “countryside” have degree 4 (and are colored light gray), while nodes in the “cities” have higher degrees (and are darker), starting from degree 5 on the outskirts and ending with 8 in the city center .
Try to choose such a speed of distribution that activation covers cities, and then does not go beyond their borders.

I find this simulation both obvious and amazing. Of course , cities maintain a better cultural level than rural areas - everyone knows that. What surprises me is that part of this cultural diversity arises simply on the basis of the topology of the social network.
This is an interesting point, I will try to explain in more detail.
Here we are dealing with cultural forms that are transmitted simply and directly from person to person. For example, manners , salon games, fashion trends, linguistic trends, rituals of small groups and products that are spread by word of mouth, plus whole packets of information that we call ideas.
(Note: the dissemination of information between people is extremely complicated by the media. It is easier to imagine a kind of technologically primitive environment, for example, Ancient Greece, where almost every spark of culture was transmitted by interaction in the physical space).
From the above simulation, I learned that there are ideas and cultural practices that can be rooted and spread in the city, but they simply are not able to spread in rural areas (mathematically they cannot). These are the same ideas and the same people. It’s not that the villagers are somehow “near”: when interacting with the same idea, they have exactly the same chances to pick it uplike the townspeople. It’s just that the idea itself cannot become viral in the countryside, because there are not many links through which it can spread.
This is perhaps the easiest to see in the field of fashion - clothes, hairstyles, etc. In the fashion network, we can fix the edge of the lattice when two people notice each other's outfits. In the city center, each person can see more than 1000 other people every day - on the street, in the subway, in a crowded restaurant, etc. In the countryside, on the contrary, each person can see only a couple dozen others. Based only on this difference , the city is able to support more fashion trends. And only the most compelling trends - with the highest transmission speed - will be able to gain a foothold outside the city.
We tend to think that if the idea is good, then ultimately it will reach everyone, and if the idea is bad, it will disappear. Of course, this is true in extreme cases, but between them there are a bunch of ideas and practices that can only become viral in certain networks. This is really awesome.
Not only cities
Here we consider the effect of network density . It is defined for a given set of nodes as the number of actual edges divided by the number of potential edges . That is the percentage of possible connections that really exist.
So, we have seen that the density of the network in urban centers is higher than in rural areas. But cities are not the only place where we find dense networks.
An interesting example is high schools. For example, for a particular district, we compare the network that exists among schoolchildren with the network that exists among their parents. The same geographical area and the same population, but one network is many times denser than another. Therefore, it is not surprising that fashion and linguistic trends spread much faster among adolescents.
Similarly, elite networks are usually much denser than non-elite networks - in my opinion, this fact is underestimated (people who are popular or influential spend more time creating networks, and therefore they have more “neighbors” than usual people). Based on the above simulations, we expect that elite networks will support some cultural forms that cannot be supported by the mainstream, simply based on mathematical laws, according to the average degree of the network. I leave you to reflect on what these cultural forms may be.
Finally, we can apply this idea to the Internet, simulating it as huge and very densetown. It is not surprising that many new types of culture thrive on the Internet, which simply cannot be supported on purely spatial networks: niche hobbies, better design standards, greater awareness of injustice, etc. And these are not only pleasant things. Just as the first cities were a hotbed of diseases that could not spread with a low population density, the Internet is also a breeding ground for malignant cultural forms such as clickbait, fake news and incitement of artificial indignation.
Knowledge
“Engaging the right expert at the right time is often the most valuable resource for creative problem solving.” - Michael Nielsen, “Inventing Discoveries”
We often think of discovery or invention as a process that occurs in the mind of a single genius. He is struck by a flash of inspiration and - eureka! - suddenly we get a new way to measure volume. Or the equation of gravity. Or a light bulb.
But if we take the point of view of a lone inventor at the time of discovery, then we look at the phenomenon from the point of view of the node . While it would be more correct to interpret the invention as a network phenomenon.
Networking is important in at least two ways. Firstly, already existing ideas must penetrate consciousness.inventor. These are quotes from a new article, a bibliographic section of a new book - giants, on whose shoulders stood Newton. Secondly, the network is critical for bringing a new idea back to the world; an invention that has not spread is hardly worth calling an “invention” at all. Thus, for both of these reasons, it makes sense to model the invention - or, in a broad sense, the growth of knowledge - as a diffusion process.
In a moment, I will present a crude simulation of how knowledge within a network can spread and grow. But first I have to explain.
At the beginning of the simulation, there are four experts in each quadrant of the grid, located as follows:
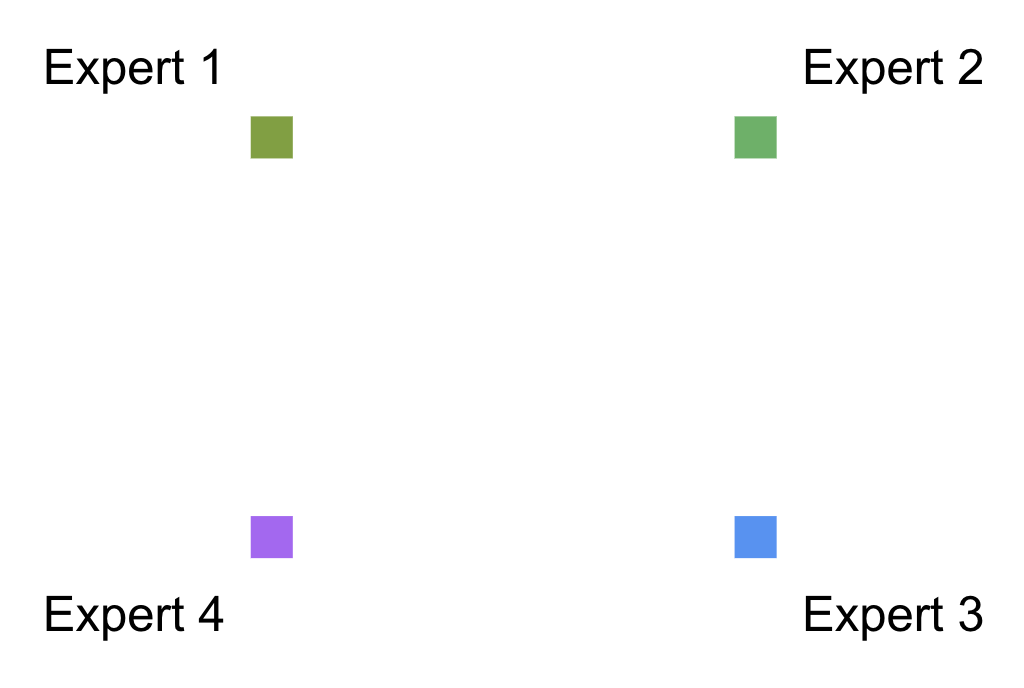
Expert 1 has the first version of the idea - let's call it Idea 1.0. Expert 2 is a person who knows how to turn Idea 1.0 into Idea 2.0. Expert 3 knows how to convert Idea 2.0 to Idea 3.0. And finally, the fourth expert knows how to bring the finishing touches to create Idea 4.0.

This is similar to a technique like origami, where methods are developed and combined with other methods to create more interesting designs. Or it may be a field of knowledge similar to physics, in which later work is based on the fundamental work of predecessors.
The essence of this simulation is that we need all four experts to contribute to the final version of the idea. And at each stage, the idea must be brought to the appropriate expert.

A few reservations. The simulation encoded many unrealistic assumptions. Here are just a few of them:
- It is assumed that ideas cannot be preserved and transmitted otherwise than from person to person (i.e. there are no books and media).
- It is assumed that there are constant experts in the population who can generate ideas, although in reality many random factors influence the occurrence of a discovery or invention.
- For all four versions of the idea, the same set of SIS parameters is used (transfer rate, percentage of immunity, etc.), although it is more realistic to probably use different parameters for each version (1.0, 2.0, etc.)
- It is assumed that the idea of N + 1 always completely supplants the idea of N, although in practice often the old and new versions circulate simultaneously, without a definitive winner.
… and many others.
Discussion
This is a ridiculously simplified model of how knowledge actually grows. Outside the scope of the model there are a lot of important details (see above). However, it reflects the essential essence of the process. And so we can, with reservations, talk about the growth of knowledge, using our knowledge of diffusion.
In particular, the diffusion model gives an understanding of how to speed up the process : it is necessary to facilitate the exchange of ideas between expert nodes. This may mean cleaning the network of dead nodes that interfere with diffusion. Or it could mean placing all the experts in a city or cluster with high network density, where ideas are spreading fast. Or just put them in one room:

So ... that’s all I can tell about diffusion.
But I have one last thought, and it is very important. It is about the growth ( and stagnation ) of knowledge in scientific communities. This idea is different in tone and content from everything that was said above, but I hope you will forgive me.
About scientific networks
The illustration shows one of the most important positive feedback cycles in the world (and it has been like this for quite some time):

The upstream cycle (K ⟶ T) is quite simple: we use new knowledge to develop new tools. For example, an understanding of the physics of semiconductors allows us to create computers.
However, the downward move requires some explanation. How does technology development lead to increased knowledge?
One way - perhaps the most direct - is when new technologies give us new ways of perceiving the world. For example, the best microscopes allow you to look deeper into the cell, throwing ideas for molecular biology. GPS trackers show how animals move. Sonar allows you to explore the oceans. Etc.
Sure, this is a vital mechanism, but there are at least two other ways from technology to knowledge. They may not be so simple, but I think they are just as important:
First one . Technology leads to economic abundance (i.e. wealth), and this allows more people to engage in the production of knowledge.
If 90% of the population of your country is engaged in agriculture, and the remaining 10% are engaged in some form of trade (or war), then people have very little free time to think about the laws of nature. Perhaps that is why in former times, science was promoted mainly by children from wealthy families.
The United States annually graduates more than 50,000 doctors of science. Instead of having a person go to work at the plant at the age of 18 (or earlier), the graduate student has to be financed up to 30 or, possibly, up to 40 years - and even then it is not clear whether his work will bring any real economic effect. But it is necessary for a person to reach the forefront in his discipline, especially in such complex fields as physics or biology.
The fact is that, from the point of view of systems, specialists are expensive. And the ultimate source of social wealth that finances these professionals is new technology: plow subsidizes the pen.
Second. New technologies, especially in the field of travel and communications, are changing the structure of social networks in which knowledge is growing. In particular, this allows experts and specialists to interact more closely with each other.
Notable inventions here include a printing press, steamboats and railways (facilitating travel and / or sending mail over long distances), telephones, airplanes and the Internet. All these technologies contribute to increasing network density, especially within specialized communities (where almost all knowledge growth occurs). For example, correspondence networks that arose among European scientists at the end of the Middle Ages, or how modern physicists use arXiv.
Ultimately, both of these paths are similar. Both increase the density of the network of specialists, which in turn leads to an increase in knowledge:

For many years I have been rather dismissive of higher education. A short stay in graduate school left an unpleasant aftertaste in the mouth. But now, when I look back and think (to ignore all personal problems), I must conclude that higher education is still extremely important.
Academic social networks (for example, research communities) are one of the most advanced and valuable structures created by our civilization. Nowhere have we accumulated a large concentration of specialists focused on the production of knowledge. Nowhere have people developed in themselves a greater ability to understand and criticize each other's ideas. This is the beating heart of progress. It is in these networks that the fire of enlightenment burns the most.
But we cannot take progress for granted. If the crisis with the irreproducibility of experiments has taught us something, it is that science can have systemic problems. This is a kind of network degradation.
Suppose we distinguish two ways of doing science: real science and careerism . Real science is practices that reliably produce knowledge. She is motivated by curiosity and characterized by honesty (Feynman: “You see, I just need to understand the world”). Careerism, in contrast, is motivated by professional ambitions and is characterized by a game of politics and scientific labels. He may look and act like a science, but does not produce reliable knowledge.
(Yes, this is an exaggerated dichotomy. Just a thought experiment. Do not blame me).
The fact is that when careerists occupy a place in the real research community, they spoil the work. They strive to promote themselves, while the rest of the community is trying to gain new knowledge and share it. Instead of striving for clarity, careerists complicate and confuse everything in order to sound more impressive. They do (as Harry Frankfurt would say) scientific bullshit. And, therefore, we could model them as dead nodes, immune to the bona fide exchange of information necessary for the growth of knowledge:

Perhaps the best model is one in which career nodes are not just immune to knowledge, but actively disseminate fake knowledge . Fake knowledge may include insignificant results, the importance of which is artificially inflated, or really false results that arise from manipulation or fabricated data.
Regardless of how we model them, careerists can certainly strangle our scientific communities.
This is similar to the nuclear chain reaction that we desperately need - we need an explosion of knowledge - only in our enriched U-235 is there too much admixture of the non-reactive isotope U-238 that suppresses the chain reaction.
Of course, there is no clear difference between careerists and real scientists. Each of us has a bit of careerism. The question is how long the network can withstand before the spread of knowledge fades.
Oh, you read it to the end. Thank you for reading.
License
CC0 All Rights Reserved. You can use this work as you see fit :).
Acknowledgments
- Kevin Kwoku and Nicky Case for thoughtful comments and suggestions on various versions of the draft.
- Nick Barr - for moral support throughout the process and for the most useful feedback about my work.
- Kita A. for pointing me to the phenomenon of percolation and the percolation threshold.
- Джеффу Лонсдейлу за ссылку на это эссе, которое (несмотря на его многочисленные недостатки) стало основным стимулом для работы над этим постом.
Образцы интерактивных эссе
- Все работы Ники Кейса, особенно «Притча о полигонах» (с Ви Харт) и «Разработка лучшего бюллетеня для голосования». Это высокая планка того, каким может быть интерактивное эссе.
- Distill.pub: исключительно качественные интерактивные описания машинного обучения.
- Классическая работа Брета Виктора «Вверх и вниз по лестнице абстракции». Я не очень хорошо справился с продвижением по лестнице, но всегда остаётся ещё одна попытка.
