Introduction

about the project

The project “Absolute exchange rate” is engaged in the analysis of paired exchange rates, the allocation of absolute exchange rates from them and their analysis. Within the framework of the project, a methodology for converting from pair rates to absolute exchange rates was obtained. For this, the absolute currency ABS is defined. All available currencies are expressed in terms of ABS.

A detailed description of the technology is given in the article “From currency pairs to absolute exchange rates” .

About problem

This article addresses the problem of a qualitative analysis of the coherence of exchange rates.
The need to study the relationship between currencies is due to the requirements for the selection of financial instruments in the investment portfolio and the ability to predict the behavior of currencies based on data on other currencies associated with them.

It is advisable to include instruments with high multidirectional connectivity in the investment portfolio. This allows you to reduce the overall risk of the portfolio.

And, if you find tools with a high degree of connectedness, then based on the behavior of some, you can predict the behavior of others.

About the experiment

Method selection

As the initial data for the experiment, there are data series with absolute exchange rates (see source file. “Absolute exchange rates” sheet ).



To study the connectivity of a series of numerical data, it is best to use Pearson correlation (see Correlation - Wikipedia ).

The correlation coefficient has a range of values ​​from “-1” to “+1”. Large negative values ​​indicate a strong multidirectional relationship. Large positive values ​​indicate strong unidirectional connectivity. The proximity of the coefficient to “0” indicates the absence of communication.

What do you want to get?

The purpose of the experiment is to obtain groups of currencies with a high degree of connectedness. Moreover, the sign of communication is also of interest.

Location

All calculations will be carried out in the Wolfram Mathematica system (see Wolfram Mathematica - Wikipedia ). And we will use Wolfram.Cloud free cloud resources .

The specified resource allows you to create online notebooks with calculations and allows you to provide access for general viewing. The notebook of this experiment is located here .

Plan

We will carry out calculations according to the following plan.

First, we calculate the correlation matrix. Columns and rows of the matrix will correspond to individual currencies. At the intersection of the column and row will be the pair correlation coefficient.

Next, we select pairs of currencies with the strongest ties. Place the selected pairs on the graph (see Graph (mathematics) - Wikipedia ).

The nodes of the graph are currencies. The edges of the graph will indicate the relationship between the currencies. The color of the rib will indicate the bond sign. Green indicates a positive relationship, and red indicates a negative relationship.

The indicated sequence of calculations will be performed both for absolute courses and for their changes. An analysis of the relationship of absolute courses allows you to explore slow processes (more than one day). An analysis of the relationship between changes in absolute exchange rates will allow us to investigate the fast connections between currencies (one day).

results

Sampling depth

The source file contains data for the last 150 days. According to them, the calculation will be made.

Currency cloud

The experiment involved 45 currencies.



A complete list of currencies can be seen on the “Currency Summary” sheet of the source file .

Absolute Rate Correlation

Above (see. Plan), it was planned to calculate the correlation matrix for absolute rates. The result is shown in the picture below.



Here, red corresponds to a positive connection, and blue to a negative one. For understanding, a gradation scale is given. Below and on the left are the currency tickers (short names).

Absolute rate dependency graph

The correlation matrix made it possible to distinguish two groups of currencies with a high degree of connectedness. To do this, pairs with a correlation higher than 0.9 were selected and transferred to the graph.



The first group gathered currencies with a high degree of dependence on the US dollar. Here are the currencies of four Arab countries trading in oil, the Hong Kong dollar and the US dollar itself. All dependencies are positive (unidirectional).

The second group gathered European currencies. In the center is the Euro itself and around it the currencies of Poland, Romania and Denmark. All dependencies are positive (unidirectional).

Relative changes in absolute rates

For further research, we calculated the series of relative changes in absolute rates. The formula for the calculations is as follows.



The difference between successive values ​​will be correlated to the earlier of the two. Thus, we will receive a relative change in the absolute rate.

Correlation of relative changes in absolute rates

As for absolute courses, we obtain a correlation matrix for relative measurements of absolute courses. We give a graphical display of the matrix.



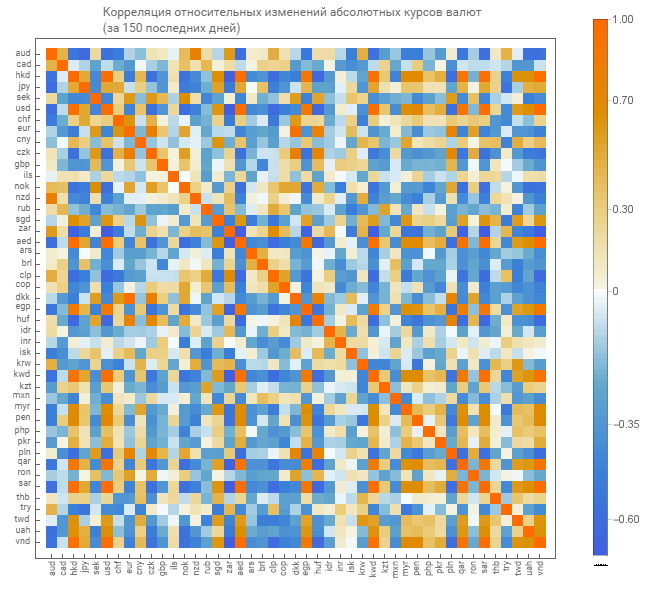
There is already a matrix of lighter tones. Which indicates a lesser degree of connectedness.

Dependency graph of relative changes in absolute rates

From the correlation matrix of relative changes, we select pairs of currencies with a high degree of connectedness. Only the sampling level here is already 0.6 (here and above, this coefficient was chosen from the consideration of a small number of pairs for output to the graph).



In the case of relative changes received 3 groups of currencies. The upper group combined the currencies of Australia and New Zealand. The lower group gathered European currencies. The middle group around the Hong Kong dollar combined the currencies of the United States, Vietnam, five Arab countries - oil exporters, South Africa and Peru.

Moreover, there is an interesting feature in the high negative dependence on the South African rand.

conclusions

As a result of the experiment, we managed to obtain the following.

Putting the correlation matrix data into a mathematical graph is a good visualization practice for the correlation matrix. Further application of this method will simplify the understanding of the relationships in the group of number series.

A formal method for clustering currency markets is found. It was possible to formally distinguish the markets of Europe, America with Asia and Oceania. This method can significantly shorten the path for revealing the mutual influences between the markets of different countries and become a good tool for a financial analyst.

The inclusion of the South African rand in the investment portfolio together with the US dollar will reduce the risks of such a portfolio.

catalogue of articles