Exotic pencil: detecting a second sound in ordinary graphite

Wake up in the morning while singing toucans, look at the weather forecast and see the same +28, put on your favorite shorts and go for a walk around the city, drive away the impudent monkeys from the garbage can, take a walk along the palm alley, sit down on a bench in front of the lake and feed the flamingos, remember about the preparation by winter and buy another shorts. For someone, such a day is not unusual, but for us (I mean the inhabitants of the continental climatic regions) this is a real exotic. What does flamingo and toucans have to do with physics, you ask? And despite the fact that physics is also not alien to exotics, manifested in processes, substances and phenomena that somehow differ from the generally accepted norm. Today we’ll talk about just one of these phenomena - the second sound that was found in ordinary graphite. What is so exotic about him how did scientists find it and should we share their enthusiasm for discovery? We will find the answers, where and usually - no, not in Google, but in the report of the research group. Go.
Theoretical retreat
The second sound is a rather funny name for the phenomenon, which only indirectly refers to the sound itself (it is slightly in contact with the sleeves, so to speak). The second sound is a quantum-mechanical phenomenon in which heat transfer proceeds in a wave-like fashion, rather than the usual diffusion. The word “sound” is present in the name of this process due to the similarity of the wave propagation of heat with a similar propagation of sound waves.
Sound waves are fluctuations in the density of molecules in matter, but the waves of the second sound are already fluctuations in the density of particle-like thermal excitations (phonons and rotons * ).
Roton * is a quasiparticle in superfluid 4 He (helium-4).Earlier manifestations of the second sound were found in a rather small list of substances and at sufficiently low temperatures:
- 2 He - liquid ( superfluid * ) helium obtained by cooling 4He below 2.1768 K;
- 4 He, 3 He, Bi (bismuth) at a temperature of 1.2 ... 4.0 K and NaF (sodium fluoride) in the solid state of aggregation at a temperature of 10 ... 20 K.
Superfluidity * is a property of a fluid with zero viscosity, which allows it to flow without loss of kinetic energy. In other words, such a substance (quantum liquid) at temperatures close to absolute zero can pass through very narrow holes and capillaries without friction.However, scientists did not stop searching for a second sound in other substances. The search yielded results - signs of a second sound were found in ordinary graphite at temperatures above 100 K.
In their study, scientists used optical measurements of heat transfer in graphite with a length scale of 5-20 microns. The observational results are completely comparable with the calculations performed earlier and theoretically indicating the presence of a second sound at ~ 1 μm scale at high temperatures (up to room temperature).
Researchers remind us that in ordinary non-metallic solids, heat is transferred by lattice vibrations or phonons *(not to be confused with photons). In an ideal (practically) crystal at a temperature of about 10 K, phonons can propagate at microscopic distances without scattering, and this leads to ballistic heat transfer.
Phonon * is a quantum of the vibrational motion of a crystal atom.At room temperature, the average length of heat transfer at the phonon is quite small due to the high speeds of phonon-phonon scattering, therefore, the heat propagates due to diffusion over macroscopic distances.
The second sound, as a phenomenon, is located somewhere between the ballistic and diffusive heat transfer. This intermediate mode is called phonon hydrodynamics. In such a situation, normal phonon-phonon scattering proceeds much more often, in which the total reduced phonon momentum is retained, and the transfer process * is less likely to occur . Transfer processes *- when quasiparticles collide in crystals, and the law of conservation of momentum is realized up to the reciprocal lattice vector. However, normal scattering alone is not enough to scatter the heat flux and return the lattice to the state of thermal equilibrium. Instead, the phonon population relaxes to a “biased” Bose-Einstein distribution, characterized by a non-zero drift velocity, which is comparable to the flow of molecules in gases. This allows thermal waves (phonon density waves) to propagate at a speed below the speed of sound.
Research results
In preparation for the actual experiments, scientists made calculations and got acquainted with some theoretical predictions made earlier. They found that a second sound should occur in the time interval between normal scattering and overshoot (τ N <t <τ U ). In accordance with theoretical predictions, the nanosecond scale of the experiment was established for graphene. And this complicates the research process due to the inability to use conventional temperature sensors to determine heat transfer. Therefore, scientists turned to lasers for help. More precisely, the method of transitional thermal gratings ( 1A ) was used, when two short (60 ps each) laser pulses intersect on the surface of the sample.
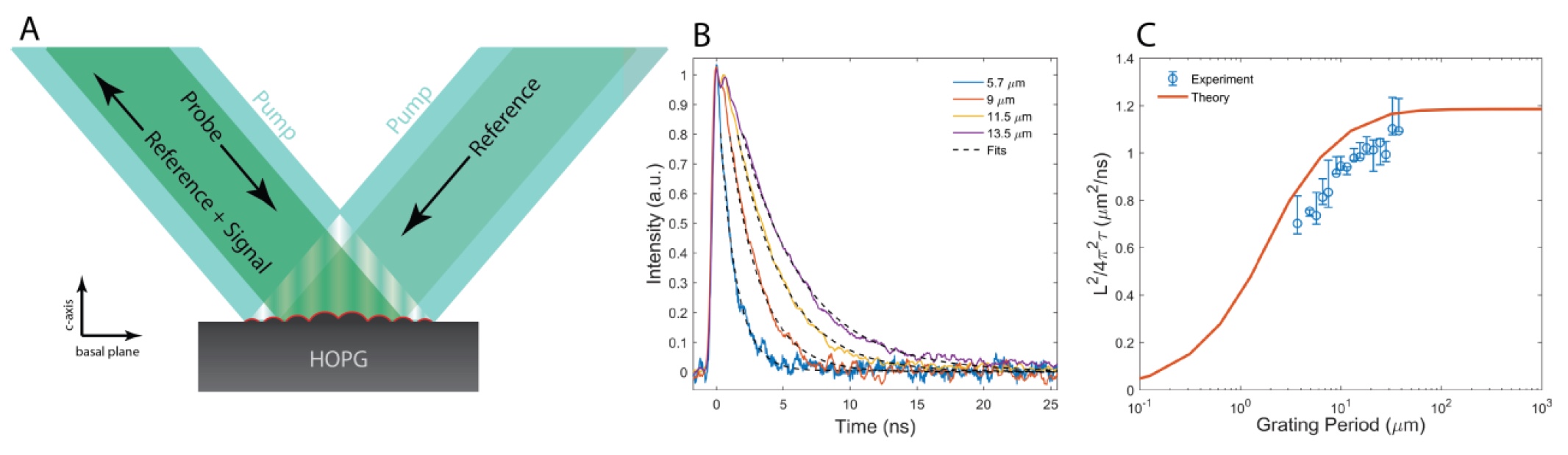
Image No. 1
The laser “handshake” forms a spatially sinusoidal heat source, the period of which ( L ) is determined by the pattern of optical interference.
Due to the thermal radiation, a “thermal lattice” is formed - a spatially sinusoidal temperature field along the surface of the sample (∆T (t, z) cos (qx), where q = 2π / L is the wave vector of the thermal lattice). Subsequently, due to heat transfer, this heat grating decays. Thermal expansion creates a coupled sinusoidal modulation of the surface displacement or “pulsation” u (t) cos (qx), which acts as a transition diffraction grating for laser radiation. Thus, the attenuation (decay) of the heat grating due to heat transfer is controlled by the time-dependent diffraction of the continuous wave probe laser. The diffracted beam is superimposed on the reference beam from the same source for optical heterodyne detection.
Highly oriented pyrolytic graphite was the protagonist of this study, that is, a sample. The sample was a polycrystal with a grain size of ~ 10 μm, and the position of the axis from all grains was perpendicular to the surface of the sample itself.
Initially, 515 nm light was used on the sample to create the initial thermal grating at an optical skin depth of ~ 30 nm. The heat transfer process proceeded in two directions: along the surface of the heat grid (in the plane) and perpendicular to the surface (transverse plane). The heat transfer in the transverse plane of graphite was ~ 300 times weaker than the transfer in the plane. Thus, the depth of thermal diffusion in the transverse plane is much smaller than the position of the heat lattice.
In accordance with the diffusion of heat (τ = L 2/ 4π 2 ⍺), in a one-dimensional medium, the decay of the transitional thermal lattice occurs exponentially. This statement was confirmed in practice: at a temperature of 300 K, signs of exponential decay ( 1B ) were detected . At L (lattice period) equal to 37.5 μm, a thermal diffusivity of 11 cm 2 / s was obtained .
With a decrease in the lattice period, the heat diffusion formula given above does not correspond to a constant value of ⍺ (thermal diffusivity). The shorter the lattice period, the slower the decay / attenuation of the transitional thermal lattice ( 1C ). And this is at variance with the predictions of the diffusion model of heat transfer.

Image No. 2
Graph 2Ait displays significant changes when the temperature drops to 85 K. At a temperature of 300 K, the signals damp monotonously, but at 85 K, damped oscillations occur when the signal can drop below zero. For heterodyne detection, a change in the sign of the transition heat lattice signal means that the spatial phase of the lattice has shifted by π. In other words, the position of the local maxima and minima of surface displacements (including temperature) are reversed. And this behavior of the transitional thermal grating is comparable to the thermal standing wave * .
Standing wave * is a wave process in distributed oscillatory systems with alternating and stable in space maxima and minima of the amplitude.In the diffusion version, heat transfer occurs from hotter to colder areas, and the maxima and minima cannot be interchanged. That is, this observation is a distinctive feature of the wave propagation of heat.
Insert on chart 2Ashows that with an increase in the lattice period, the frequency of wave-like dynamics decreases. The observed linear relationship indicates a speed of 3200 m / s. This is an important observation, since often the transitional thermal grating signals can contain oscillations due to surface acoustic waves, but their speed is much lower. Given that the speed of surface acoustic waves is approximately 1480 m / s, which is close to the slow transverse velocity, while the fast transverse speed is 14700 m / s, and the longitudinal velocity is even higher. It is also worth noting that if there were acoustic waves, they would not disappear with an increase in the background temperature or the lattice period.
In order to simulate such dynamics, scientists applied the linearized Boltzmann transport equation with a full three-phonon scattering matrix in a one-dimensional transition heat lattice. Previously, a similar method was used to determine the thermal conductivity of graphene and graphite. However, this technique was somewhat limited and could not be applied if it were not for new studies that described a method for calculating the frequency Green's functions for unsteady and inhomogeneous Boltzmann transport. Figure 2B shows precisely these Green functions that describe the reaction of a phonon population to a heat source in the form of a harmonic plane wave.
The calculations carried out by scientists taking into account the above methods made it possible to understand the time dependence of the amplitude of the thermal grating. Calculations at a temperature of 300 K and various lattice periods showed the exponential attenuation of the transitional thermal lattice, which is fully consistent with the experiment ( 1C ). At a temperature of 85 K, the frequency Green's function gives a resonant peak ( 2B ), which is a hallmark of the second sound and leads to damping oscillations ( 2C ). All the calculated data are completely comparable with the experimental ones - even the fact of the disappearance of the second sound at large periods of the transitional thermal lattice.
The calculations showed that the speed of the second sound (given the position of the peak of the frequency resonance at 2C) is 3650 m / s. Such an indicator distinguishes graphite from a number of other materials where a second sound was detected. In them, the speed of the second sound was slower than the minimum speed of phonons. Graphite is also surprising in that it has a very low speed of the slow transverse acoustic mode. And the impressive anharmonicity and density of states of this mode lead to intense normal scattering and create conditions for the hydrodynamic transfer of phonons.
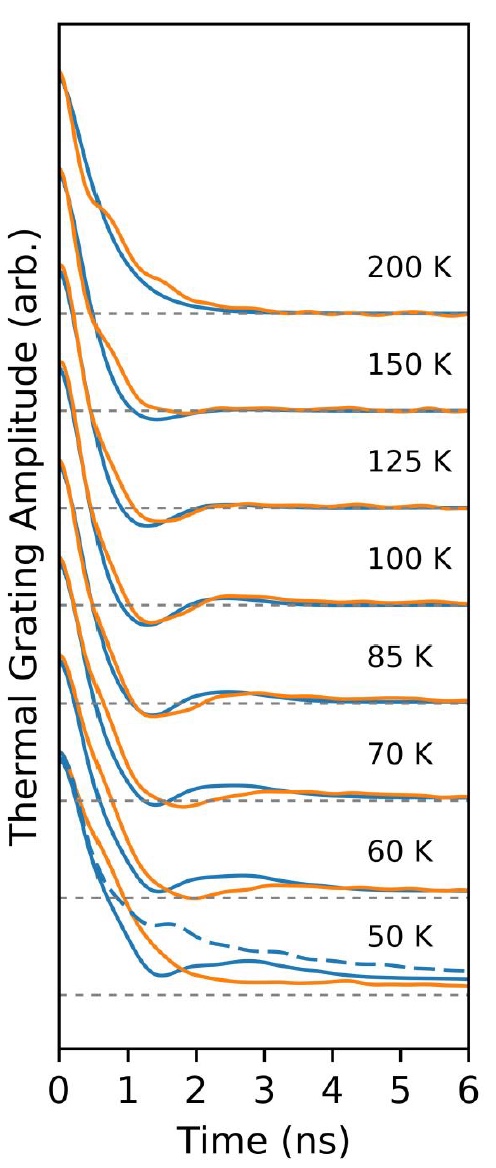
Image No. 3
Graph above ( No. 3) displays the data of the transitional heat lattice at a constant period of 10 μm and at different temperatures. Vibrational behavior was observed at 104 K and even at 125 K, but when it reaches a temperature of 150 K, it completely disappears. The same thing happens when the temperature drops below 50 K.
Also, the graph shows a simulated response at 50 K in the ballistic mode, when the phonon scattering rate was set to zero. And here it is clear that the failure in the response in ballistic mode disappears. That is, the disappearance of the second sound at a temperature of 50 K corresponds to what is expected during the transition to the ballistic mode.
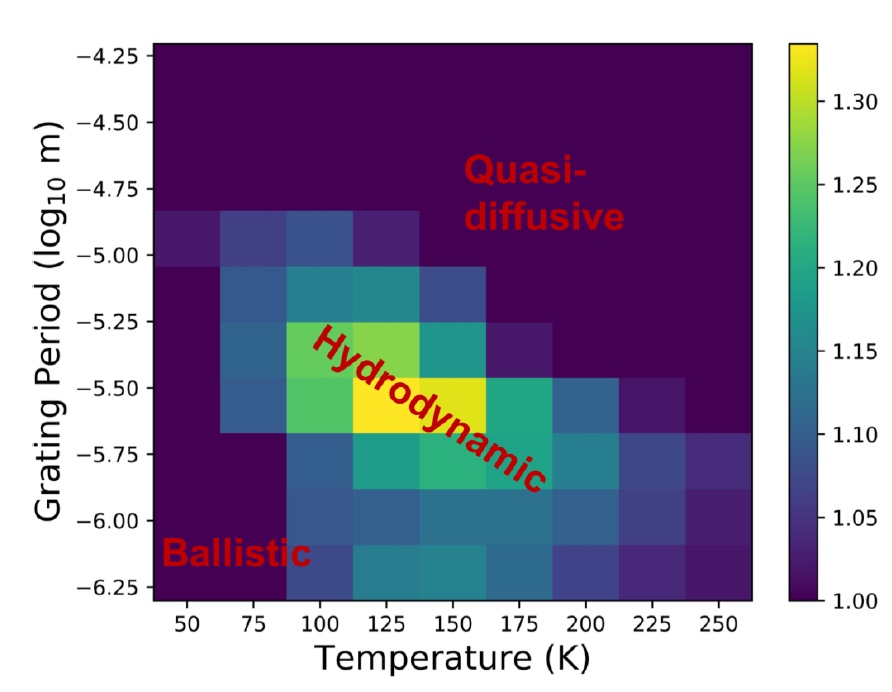
Image No. 4
Modeling the data showed that the appearance of a second sound can be expected in the temperature range from 50 to 250 K. The higher the temperature, the shorter the heat transfer length: at L = 10 μm, the temperature "ceiling" is about 150 K, but already at L = 1.5 μm the second sound will be observed up to 250 K.
At low temperatures and small lattice periods, phonon scattering disappears, and heat transfer becomes ballistic. If there are high temperatures and long periods, the heat transfer slowly passes into the "quasi-diffusion" mode.
Graphite also excelled in terms of isotopes. That is, previously the second sound was observed only in isotopically pure solids (if you do not take into account the controversial, according to scientists, observations in SrTiO 3) But the graphite used in the experiment is not isotopically pure, which indicates the unique nature of the phonon hydrodynamics of this substance.
For a more detailed acquaintance with the nuances, details, methodology and calculations of the study, I strongly recommend that you look into the report of scientists and additional materials to it.
Epilogue
Sometimes exotic phenomena or properties are hidden in the most ordinary and unremarkable objects. This study was a confirmation of this. The second sound, being an exotic phenomenon, was previously observed only in very “strange” substances and under very extreme conditions.
Scientists consider their work to be important for the general study of phonon hydrodynamics. Understanding of such things will make it possible to use graphite and graphene as heat-dissipating materials in microelectronics. Scientists also believe that their work will accelerate the study of manipulation and control of transport processes in the micro and nanoscale.
We know so much about the things around us, but at the same time, such studies suggest otherwise. Is there a limit to this knowledge? As long as there is the curiosity and enthusiasm of scientists - no.
Thank you for your attention, remain curious and have a good working week, guys.
Thank you for staying with us. Do you like our articles? Want to see more interesting materials? Support us by placing an order or recommending it to your friends, a 30% discount for Habr users on a unique analogue of entry-level servers that we invented for you: The whole truth about VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps from $ 20 or how to divide the server? (options are available with RAID1 and RAID10, up to 24 cores and up to 40GB DDR4).
VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps until the summer for free when paying for a period of six months, you can order here .
Dell R730xd 2 times cheaper? Only here2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV from $ 249 in the Netherlands and the USA! Read about How to Build Infrastructure Bldg. class using Dell R730xd E5-2650 v4 servers costing 9,000 euros for a penny?
