Perlin noise, procedural content generation and interesting space
- Transfer
Probably the worst thing that happened in the field of procedural content generation (assuming that this is indeed the area of procedural content generation, which I’m not entirely sure of) is Perlin’s noise. Perlin's noise is incredibly well suited (at least if you don't look too closely) to generate interesting landscapes. In the subreddit / r / proceduralgeneration, a week does not pass without someone publishing a "procedural generation system", which turns out to be Perlin's noise visualized in different colors. (During the writing of this article, two such posts appeared!)

I don't want to humiliate Perlin’s noise. This is an incredibly useful tool for procedural generation, which has become an entry point in this area for many people, including me. But at the same time, it is very confusing, because it implies that procedural generation is much simpler than it really is. Most of the weekly posts on “procedural generation systems” in / r / proceduralgeneration disappear without a trace when their authors find that the next step in procedural generation is much more complicated. The truth is, Perlin’s noise was a kind of happy coincidence. It is great for generating interesting landscapes, but there are no systematic or repeatable reasons.
Mike Cook recently posted a tutorialcontrasting the space of possibilities with the space of generation. If you create a generation system to create X, then the space of possibilities is equal to all possible Xs, and the generation space is all X that your system can actually generate. Mike illustrates this idea with Minecraft:
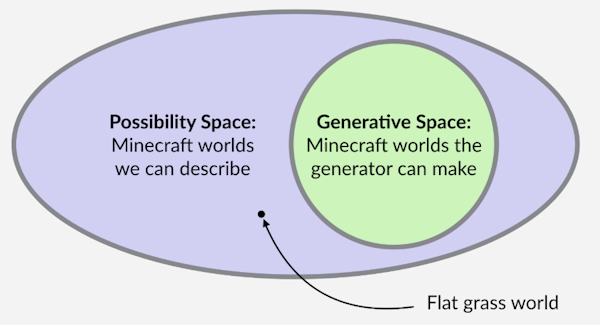
In the case of my Dragons Abound game, the space of possibilities includes every possible map, including many degenerate cases, for example, a map consisting entirely of the ocean with one small island. Generation space - this is the least space of all cards that Dragons Abound can generate really . Due to the various rules used, Dragons Abound cannot generate a map from the ocean with a small island, so this map is not in the game generation space. Comparing the space of possibilities with the space of generation is an interesting and useful look at procedural generation, so I recommend that you read Mike's postin which this idea is explained in more detail, and there are also several interactive examples.
In addition to the space of possibilities and the space of generation, it is also useful to think of an “interesting space”. If we create X, then this is the space of all interesting X. That is, in the case of my game, this is the space of all interesting fantasy cards. An interesting space is a subset of the space of possibilities and, we hope, intersects with the generation space - for example, I hope that at least some of the cards generated by my game turn out to be interesting.
Before moving on, I readily admit that “interest” is a vague and subjective concept. My and your ideas about interesting things most likely do not coincide. I don’t even always know what will seem interesting to me - I often see something new and find it interesting, although I did not think that I would like it until I saw it. Worse, the more interesting we see, the less interesting it becomes. When you see an interesting feature on twenty cards in a row, it no longer seems interesting. Therefore, "interest" is not so easy to grasp. In the future I’ll talk in more detail about what makes things interesting (and in the past I had something to say about the close idea of a space of creativity), but so far this is not very important. It is enough for us to agree that some things are more interesting than others, and that more interesting things are in an “interesting space”, while less interesting things are not.
Is it possible to illustrate an interesting space in the same way that Mike showed the space of possibilities and the space of generation? As suggested above, an interesting space is a subset of the space of possibilities, which (if you're lucky) intersects with the generation space:

A good generator intersects strongly with an interesting space; a bad generator is weak.
These patterns are just a metaphor, but within the framework of this metaphor I want to ask the following question: have I correctly indicated the shapes of different spaces? The shape of the space of possibilities is not really important, it just has to contain two other spaces. But the forms of the generation space and the interesting space are more interesting (sic) questions. I painted both of them as single compact forms within the space of possibilities. Is this reasonable?
I believe that designating the generation space as a compact ellipse is a good choice for many procedural generators, and especially for something like Perlin noise. The form implies that the generator creates all the solutions within a single clearly defined and compact space. If the generator can create X, then it can usually create all the neighbors of X. Usually there are no large “holes” or strange distortions in the generation space.
Generation spaces usually look like this for two reasons. Firstly, at the level of practical application, a generator is a small amount of code associated with a space of possibilities. Currently Dragons Aboundcontains about 28 thousand lines of source code. Compared to many other procedural card generators, this is a lot (perhaps even a record), but it is still extremely small compared to the space of possibilities of all fantasy cards. Therefore, no matter how smart the game code is, its generation space will occupy only a small part of the space of possibilities, and since computer code is, by definition, algorithmic and deterministic, this space will be relatively compact. That is, if the game can create one type of card, it will almost certainly create many other similar cards.
The second reason that generation spaces are compact is strategic. For me, the goal of creating Dragons Abound- This is the generation of interesting maps so that they intersect as much as possible with interesting space. And it’s hard to get into an interesting space, it is very small compared to the space of possibilities. In fact, it is very, very small. All these spaces have a huge number of dimensions, and the size of the space essentially grows as a power of the number of dimensions. The real relationship between the interesting space and the space of possibilities looks something like this:
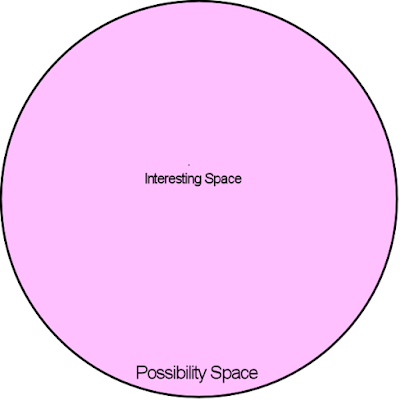
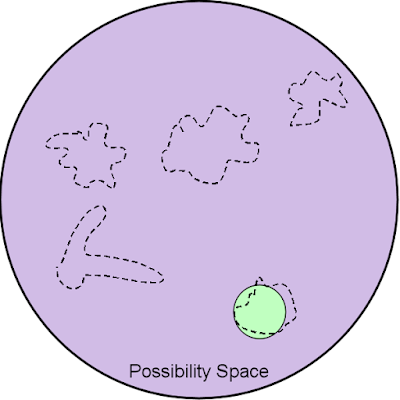
Only an interesting space is much, much smaller. This forces procedural generation to adhere to certain strategies. For example, why does the game not create completely random maps? Then the generation space would look like this:
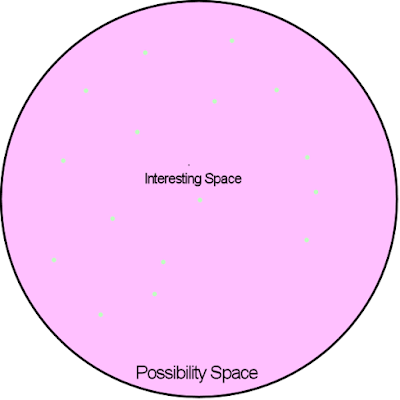
Only green dots are much smaller. The chances of getting from one of the random cards into a tiny interesting space are essentially zero. To increase the chances of getting into an interesting space, the creator of procedural generation uses knowledge about the space of possibilities and interesting space to control generation - the creator shifts the generation space so that it is mainly located in the neighborhood of the interesting space, and not just randomly distributed.
For all these reasons, it will be logical to perceive the generation space as a connected, compact area.
But I believe that drawing such an interesting space would probably be completely wrong. It should be described as a scattered, divided set of strange-shaped areas. Why? Because (1) things can be interesting for various orthogonal reasons, and (2) interest is a discontinuous function.
Consider, for example, these two map fragments:

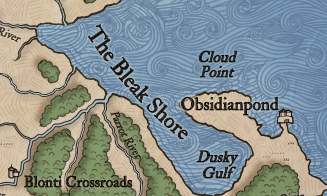
The first fragment is interesting in that the coastline is intricately detailed and contains many small islands. The second fragment has a boring, smooth coastline, but the coast has interesting features - it is uninhabited and has the ominous name “Bleak Shore”. In a sense, both of these fragments are interesting, but for completely different reasons. Therefore, we will not expect that these two parts of the interesting space will be neighbors.
Moreover, these two parts of the interesting space are most likely not even connected. In no way will it be possible to gradually convert the first interesting map into a second interesting map without creating several uninteresting maps along the way. Therefore, these two parts of the interesting space are separated.
So, an interesting space is not a single area, but a set of divided areas. Does every such interesting space have smooth, compact shapes?
I repeat, I do not declare that I can give a complete definition of "interest." But in some aspects, we can agree on several points. Firstly, if X is interesting, then this does not mean that 2X will be twice as interesting. Take the example of the Sad Coast - one area of the mysterious coast on the map is interesting, but a dozen of them will be very uninteresting. You can probably come up with other examples of how “interest” behaves in a strange and counterintuitive way. So, interest has some elements of discontinuity - it is not a smooth function that changes in a rational and predictable way when moving through the space of possibilities.
All this makes us understand that we should designate an interesting space as a series of divided areas of a strange shape.
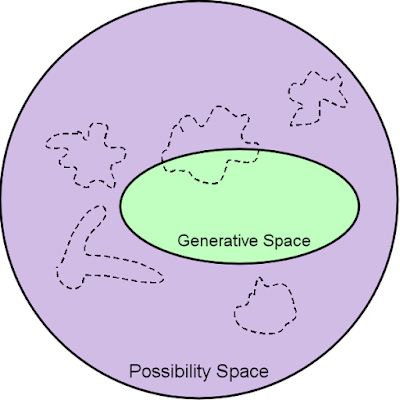
You are already starting to understand why creating a good procedural generator is a difficult task. Due to the way the algorithms work and the limitations of our capabilities, the generation space will be small and compact. At the same time, we want to get into as many strange and scattered areas of interesting space as possible. It's amazing that we even manage to get into them!
Now let me get back to the topic of Perlin noise. What will this scheme look like for Perlin noise generation space in landscape space? I think something like this:
Perlin's noise generator has more intersection with a particular interesting space within the universe of all possible landscapes. And this is excellent - almost everything that can be created using Perlin noise falls into this area and looks pretty interesting.
But this quick success is misleading. If you are new to procedural generation, you will see how Perlin noise works well and most likely decide that Perlin noise is a magic wand for generating all kinds of interesting landscapes, not to mention all types of procedural generation. But as the diagram shows, Perlin’s noise generation space is actually far from many other parts of the interesting landscape space. The standard second step in procedural landscape generation is the addition of rivers. But if you try to realize the rivers with the help of Perlin noise, you will find that it is impossible! In no way can one expand the boundaries of Perlin's noise generation space to reach distant interesting spaces containing realistic rivers.
Perlin's noise is misleading in another sense. Earlier, I talked about the fact that the interesting space is so small that if you want to get into it, you need to have certain knowledge about the space of possibilities and interesting space in order to control procedural generation. But Perlin's noise algorithm does not know anything about landscapes, geological processes, what people find interesting, and yet, somehow, it works well without this knowledge! The noise of Perlin turned out to be the exception, confirming the rule (*). But if you are new to procedural generation, then you most likely don’t know this rule. In fact, you are deducing an erroneous rule - all procedural generation as a whole should work like Perlin noise.
(* It was not just by chance that he “turned out” to be an exception. Perlin noise became a popular starting point precisely because it is an exception. It is very easy to start with Perlin noise without having to study a large amount of information about landscapes.)
Consider another popular starting point in procedural content generation: dungeon schemes. Unlike landscape generation, dungeon schemes do not have an algorithm similar to Perlin noise, which magically creates solutions in an interesting space. Based on what we know about the generation space and the interesting space, we can guess that the dungeon generators should either (1) include specific knowledge about the later days and the interestingness, or (2) create mostly uninteresting dungeons. Indeed, if you look at the dungeon generators published over the past year in / r / proceduralgeneration, you will see that most of them do not contain any knowledge about dungeons other than checking the connection of all rooms, and therefore the data displayed by these projects is more likely random than interesting .
So, if you consider that you more or less agree with what I wrote, then what lessons can be learned from this concept of an interesting space?
If you are just starting to work with procedural generation, then I recommend that you think about fun. What will make the output interesting? What does the algorithm need to understand in order to produce data that is often interesting? What other way to output data might be interesting? What new algorithm do I need to generate this kind of interest? How to combine / balance it with the first algorithm?
For example, if I wanted to create a dungeon generator, then I thought about the dungeons for a while, and decided that in my opinion the dungeons are interesting if:
Now you can think about how the level of underground warehouses should look like, how the algorithm for the procedural generation of variations of this theme might look like, and how monsters can change this scheme. I believe that thinking about such issues will allow you to learn more about procedural generation than the implementation of another landscape generator on Perlin noise or a dungeon generator from random rooms and corridors.

I don't want to humiliate Perlin’s noise. This is an incredibly useful tool for procedural generation, which has become an entry point in this area for many people, including me. But at the same time, it is very confusing, because it implies that procedural generation is much simpler than it really is. Most of the weekly posts on “procedural generation systems” in / r / proceduralgeneration disappear without a trace when their authors find that the next step in procedural generation is much more complicated. The truth is, Perlin’s noise was a kind of happy coincidence. It is great for generating interesting landscapes, but there are no systematic or repeatable reasons.
Mike Cook recently posted a tutorialcontrasting the space of possibilities with the space of generation. If you create a generation system to create X, then the space of possibilities is equal to all possible Xs, and the generation space is all X that your system can actually generate. Mike illustrates this idea with Minecraft:

In the case of my Dragons Abound game, the space of possibilities includes every possible map, including many degenerate cases, for example, a map consisting entirely of the ocean with one small island. Generation space - this is the least space of all cards that Dragons Abound can generate really . Due to the various rules used, Dragons Abound cannot generate a map from the ocean with a small island, so this map is not in the game generation space. Comparing the space of possibilities with the space of generation is an interesting and useful look at procedural generation, so I recommend that you read Mike's postin which this idea is explained in more detail, and there are also several interactive examples.
In addition to the space of possibilities and the space of generation, it is also useful to think of an “interesting space”. If we create X, then this is the space of all interesting X. That is, in the case of my game, this is the space of all interesting fantasy cards. An interesting space is a subset of the space of possibilities and, we hope, intersects with the generation space - for example, I hope that at least some of the cards generated by my game turn out to be interesting.
Before moving on, I readily admit that “interest” is a vague and subjective concept. My and your ideas about interesting things most likely do not coincide. I don’t even always know what will seem interesting to me - I often see something new and find it interesting, although I did not think that I would like it until I saw it. Worse, the more interesting we see, the less interesting it becomes. When you see an interesting feature on twenty cards in a row, it no longer seems interesting. Therefore, "interest" is not so easy to grasp. In the future I’ll talk in more detail about what makes things interesting (and in the past I had something to say about the close idea of a space of creativity), but so far this is not very important. It is enough for us to agree that some things are more interesting than others, and that more interesting things are in an “interesting space”, while less interesting things are not.
Is it possible to illustrate an interesting space in the same way that Mike showed the space of possibilities and the space of generation? As suggested above, an interesting space is a subset of the space of possibilities, which (if you're lucky) intersects with the generation space:

A good generator intersects strongly with an interesting space; a bad generator is weak.
These patterns are just a metaphor, but within the framework of this metaphor I want to ask the following question: have I correctly indicated the shapes of different spaces? The shape of the space of possibilities is not really important, it just has to contain two other spaces. But the forms of the generation space and the interesting space are more interesting (sic) questions. I painted both of them as single compact forms within the space of possibilities. Is this reasonable?
I believe that designating the generation space as a compact ellipse is a good choice for many procedural generators, and especially for something like Perlin noise. The form implies that the generator creates all the solutions within a single clearly defined and compact space. If the generator can create X, then it can usually create all the neighbors of X. Usually there are no large “holes” or strange distortions in the generation space.
Generation spaces usually look like this for two reasons. Firstly, at the level of practical application, a generator is a small amount of code associated with a space of possibilities. Currently Dragons Aboundcontains about 28 thousand lines of source code. Compared to many other procedural card generators, this is a lot (perhaps even a record), but it is still extremely small compared to the space of possibilities of all fantasy cards. Therefore, no matter how smart the game code is, its generation space will occupy only a small part of the space of possibilities, and since computer code is, by definition, algorithmic and deterministic, this space will be relatively compact. That is, if the game can create one type of card, it will almost certainly create many other similar cards.
The second reason that generation spaces are compact is strategic. For me, the goal of creating Dragons Abound- This is the generation of interesting maps so that they intersect as much as possible with interesting space. And it’s hard to get into an interesting space, it is very small compared to the space of possibilities. In fact, it is very, very small. All these spaces have a huge number of dimensions, and the size of the space essentially grows as a power of the number of dimensions. The real relationship between the interesting space and the space of possibilities looks something like this:

Only an interesting space is much, much smaller. This forces procedural generation to adhere to certain strategies. For example, why does the game not create completely random maps? Then the generation space would look like this:

Only green dots are much smaller. The chances of getting from one of the random cards into a tiny interesting space are essentially zero. To increase the chances of getting into an interesting space, the creator of procedural generation uses knowledge about the space of possibilities and interesting space to control generation - the creator shifts the generation space so that it is mainly located in the neighborhood of the interesting space, and not just randomly distributed.
For all these reasons, it will be logical to perceive the generation space as a connected, compact area.
But I believe that drawing such an interesting space would probably be completely wrong. It should be described as a scattered, divided set of strange-shaped areas. Why? Because (1) things can be interesting for various orthogonal reasons, and (2) interest is a discontinuous function.
Consider, for example, these two map fragments:


The first fragment is interesting in that the coastline is intricately detailed and contains many small islands. The second fragment has a boring, smooth coastline, but the coast has interesting features - it is uninhabited and has the ominous name “Bleak Shore”. In a sense, both of these fragments are interesting, but for completely different reasons. Therefore, we will not expect that these two parts of the interesting space will be neighbors.
Moreover, these two parts of the interesting space are most likely not even connected. In no way will it be possible to gradually convert the first interesting map into a second interesting map without creating several uninteresting maps along the way. Therefore, these two parts of the interesting space are separated.
So, an interesting space is not a single area, but a set of divided areas. Does every such interesting space have smooth, compact shapes?
I repeat, I do not declare that I can give a complete definition of "interest." But in some aspects, we can agree on several points. Firstly, if X is interesting, then this does not mean that 2X will be twice as interesting. Take the example of the Sad Coast - one area of the mysterious coast on the map is interesting, but a dozen of them will be very uninteresting. You can probably come up with other examples of how “interest” behaves in a strange and counterintuitive way. So, interest has some elements of discontinuity - it is not a smooth function that changes in a rational and predictable way when moving through the space of possibilities.
All this makes us understand that we should designate an interesting space as a series of divided areas of a strange shape.

You are already starting to understand why creating a good procedural generator is a difficult task. Due to the way the algorithms work and the limitations of our capabilities, the generation space will be small and compact. At the same time, we want to get into as many strange and scattered areas of interesting space as possible. It's amazing that we even manage to get into them!
Now let me get back to the topic of Perlin noise. What will this scheme look like for Perlin noise generation space in landscape space? I think something like this:

Perlin's noise generator has more intersection with a particular interesting space within the universe of all possible landscapes. And this is excellent - almost everything that can be created using Perlin noise falls into this area and looks pretty interesting.
But this quick success is misleading. If you are new to procedural generation, you will see how Perlin noise works well and most likely decide that Perlin noise is a magic wand for generating all kinds of interesting landscapes, not to mention all types of procedural generation. But as the diagram shows, Perlin’s noise generation space is actually far from many other parts of the interesting landscape space. The standard second step in procedural landscape generation is the addition of rivers. But if you try to realize the rivers with the help of Perlin noise, you will find that it is impossible! In no way can one expand the boundaries of Perlin's noise generation space to reach distant interesting spaces containing realistic rivers.
Perlin's noise is misleading in another sense. Earlier, I talked about the fact that the interesting space is so small that if you want to get into it, you need to have certain knowledge about the space of possibilities and interesting space in order to control procedural generation. But Perlin's noise algorithm does not know anything about landscapes, geological processes, what people find interesting, and yet, somehow, it works well without this knowledge! The noise of Perlin turned out to be the exception, confirming the rule (*). But if you are new to procedural generation, then you most likely don’t know this rule. In fact, you are deducing an erroneous rule - all procedural generation as a whole should work like Perlin noise.
(* It was not just by chance that he “turned out” to be an exception. Perlin noise became a popular starting point precisely because it is an exception. It is very easy to start with Perlin noise without having to study a large amount of information about landscapes.)
Consider another popular starting point in procedural content generation: dungeon schemes. Unlike landscape generation, dungeon schemes do not have an algorithm similar to Perlin noise, which magically creates solutions in an interesting space. Based on what we know about the generation space and the interesting space, we can guess that the dungeon generators should either (1) include specific knowledge about the later days and the interestingness, or (2) create mostly uninteresting dungeons. Indeed, if you look at the dungeon generators published over the past year in / r / proceduralgeneration, you will see that most of them do not contain any knowledge about dungeons other than checking the connection of all rooms, and therefore the data displayed by these projects is more likely random than interesting .

So, if you consider that you more or less agree with what I wrote, then what lessons can be learned from this concept of an interesting space?
- Procedural generation is fundamentally complex because the interesting space is a very small and difficult to hit target.
- Despite the occasional exceptions like Perlin noise, one should not expect that simple, naive algorithms will successfully generate interesting content. Good procedural generation should include and use an extensive, in-depth knowledge of the subject area and an understanding of what makes the content interesting.
- But even in the best generation algorithms, the generation space is compact, and the interesting space is not, therefore, it is expected that procedural generation will often miss, and therefore it is necessary to build the systems accordingly.
- In complex subject areas, interesting space is divided and has a strange shape. You should not expect that an algorithm or approach that works well in one part of an interesting space will necessarily work just as well in another part. Therefore, we should expect that procedural generation will include many different algorithms using different parts of the interesting space.
If you are just starting to work with procedural generation, then I recommend that you think about fun. What will make the output interesting? What does the algorithm need to understand in order to produce data that is often interesting? What other way to output data might be interesting? What new algorithm do I need to generate this kind of interest? How to combine / balance it with the first algorithm?
For example, if I wanted to create a dungeon generator, then I thought about the dungeons for a while, and decided that in my opinion the dungeons are interesting if:
- They look like they were created to become warehouses, prison cells
and other underground infrastructure of a large castle. - Later they were filled with monsters and rebuilt by them to satisfy their needs for shelter, food, water, protection from attacks, etc.
Now you can think about how the level of underground warehouses should look like, how the algorithm for the procedural generation of variations of this theme might look like, and how monsters can change this scheme. I believe that thinking about such issues will allow you to learn more about procedural generation than the implementation of another landscape generator on Perlin noise or a dungeon generator from random rooms and corridors.
