Quantum computing in games, or going crazy seriously
If you live among crazy people, you have to learn to be crazy
yourself. Have you ever tried to "learn to be crazy"? Non-trivial task. You won’t even find a normal technique, because everyone goes crazy in his own way. My first attempt: conspiracy theory. The theory does not involve practice, which means that you don’t have to work hard. Again, in any situation, no one will suffer.
So, heretical theory: after 5 years, Page and Green will decide who will be the main thing in Google, and they will do it with the help of the game. Each of them has a group of researchers. AlphaGo team with theirfighting neural networks pulled rivals in Go. Opponents were forced to look for new methods, and still found an instrument of total superiority: quantum computing.
Can I use Quantum Computing for games? Easy. Let us show for example that the game "fox hunter" can be "solved" in 6 moves. For the sake of credibility, we restrict ourselves to 15 qubits (the online editor quirk does not emulate for more than fifteen), for the sake of simplicity, we ignore the limitations of the processor architecture and error correction.
Extremely simple. There are five holes arranged in a row (we number them as 0-1-2-3-4). In one of them is a fox. Every night, the fox moves to the next mink left or right. Each morning, the hunter can check one hole to choose from. The hunter's task is to catch the fox. The fox's task is to survive. In theory, a fox can run from a hunter forever. In practice, there is a winning strategy: check holes 1-2-3-1-2-3. Only this strategy will I test.
Let's start with the initiation of qubits 0-1-2-3-4 (5 holes). Here you can edit.
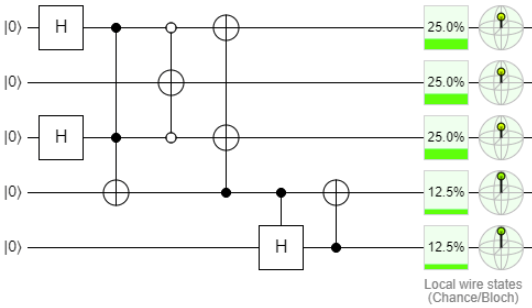
In fact, after initiation, we have a system in which, after measurement, strictly one qubit will be single. The probabilities of “unity” differ for each qubit, but in our case this is not critical. We must leave room for discussion of the scheme (and our theory at the same time).
On Q #, we get code like this:
TestStrategy will test our strategy 1-2-3-1-2-3, InitFoxHoles () is responsible only for the initiation of fox holes. Let's check the initiation. Copy TestStrategy, start the initiation, measure the first 5 qubits and return their values.
We will run the test a thousand times (multiple runs are typical of quantum algorithms, in some places even necessary). Call code - under the spoiler, results: on the screen below.

Something went wrong. An almost uniform distribution was expected. The reason is simple: in step 3, I inverted the third qubit, instead of the first: (Controlled (X)) ([register [0], register [2]], register [3]);not good old copy-paste.
We fix the code, run the test:

Already better. The code can be seen in the turnip, version Commit 1 .
Select the fifth qubit (the numbering starts from above) under the current direction of the fox. We agree that zero means a downward movement, a unit means an upward movement. Obviously, if the fox is already in the zero hole - it should move down. If the fox is in the fourth hole, it moves up. In other cases, the fox can move up and down. According to these simple rules, we can set the “qubit of the current direction” to 0, 1, or a superposition of zero and one. We look at the code in the repository, Commit 2 .

Scheme in the editor.

Scheme in the editor .
The code can be viewed in Commit 3 .
Finally, we select the sixth qubit for the status of the game (the fox is free / the fox is not free). The unit corresponds to a free fox. We will make further moves only with a single status qubit.
The qubits 7,8,9,10,11 will keep a history of moves. After each move, we are going to swap one of them with a qubit of the current direction (this will allow us to store the history of moves and reset the qubit of the current direction before each move).

Scheme attached .
We look Commit 4 .
We have an error in the circuit. Since we test the strategy 1-2-3-1-2-3, we check each hole twice. Accordingly, having caught the fox on the first move, we will go through the status qubit twice (on the first move and fourth).
To avoid this situation, we use 12 qubits to fix the status after moves 4-5-6. In addition, we add the definition of victory: if at least one of the status qubits turns to zero, we won.

The final scheme .

Commit 5 .
In principle, the scheme can be optimized both in the number of qubits and in the number of operations. The trivial optimization for the number of qubits is to get rid of qubit-13, returning only 6 and 12. Optimization for operations - to make the first shot immediately after initiation. However, let’s leave this work to Google engineers.
As you can see, anyone who is superficially familiar with quantum computing can safely play the "fox hunter." If we had a little more qubits, we could find the optimal solution, and not check the existing one. It is entirely possible that tic-tac-toe (and their quantum version), checkers, chess, Go will fall next.
At the same time, the issue of "solvability" of games like DotA, Starcraft and Doom remains open. For quantum computing, the storage of the entire history of clicks is characteristic. We take an APM (Actions Per Minute) of 500, multiply by the number of players, multiply by the number of minutes, add the randomness of the game itself - the number of qubits required to store all the information grows too quickly.
So, choosing a game in a small competition between Brin and Page can play a decisive role. However, the generation of a “equally difficult” game for classical and quantum computers deserves its own theory.
yourself. Have you ever tried to "learn to be crazy"? Non-trivial task. You won’t even find a normal technique, because everyone goes crazy in his own way. My first attempt: conspiracy theory. The theory does not involve practice, which means that you don’t have to work hard. Again, in any situation, no one will suffer.
How to create conspiracy theories?
Creating a conspiracy theory is relatively simple. We need an idea that is simple enough to be accepted by 90% of the population. It should be controversial so that 5% of the population can explain 90% what idiots they are. Finally, we need some research that these 95% of people don’t understand, but which are used by 90% as an argument "people have proved smarter than us ...".
Quantum computing is a great area for such a study. You can roll up a simple scheme, but the word "quantum" will add weight to the results.
The object of study is a game, for the object is due to simple and familiar youth. Who is involved in quantum computing and games? Google
Quantum computing is a great area for such a study. You can roll up a simple scheme, but the word "quantum" will add weight to the results.
The object of study is a game, for the object is due to simple and familiar youth. Who is involved in quantum computing and games? Google
So, heretical theory: after 5 years, Page and Green will decide who will be the main thing in Google, and they will do it with the help of the game. Each of them has a group of researchers. AlphaGo team with their
Can I use Quantum Computing for games? Easy. Let us show for example that the game "fox hunter" can be "solved" in 6 moves. For the sake of credibility, we restrict ourselves to 15 qubits (the online editor quirk does not emulate for more than fifteen), for the sake of simplicity, we ignore the limitations of the processor architecture and error correction.
rules
Extremely simple. There are five holes arranged in a row (we number them as 0-1-2-3-4). In one of them is a fox. Every night, the fox moves to the next mink left or right. Each morning, the hunter can check one hole to choose from. The hunter's task is to catch the fox. The fox's task is to survive. In theory, a fox can run from a hunter forever. In practice, there is a winning strategy: check holes 1-2-3-1-2-3. Only this strategy will I test.
Building a scheme
Let's start with the initiation of qubits 0-1-2-3-4 (5 holes). Here you can edit.

In fact, after initiation, we have a system in which, after measurement, strictly one qubit will be single. The probabilities of “unity” differ for each qubit, but in our case this is not critical. We must leave room for discussion of the scheme (and our theory at the same time).
On Q #, we get code like this:
operation TestStrategy () : (Result)
{
let res = Zero;
using(qubits=Qubit[16])
{
// 0..4 - holes
// 5 - current movement direction. Zero means "go down", One means "go up"
// 6 - Game status. 1 means "fox is free, go further"
// 7,8,9,10, 11 - movements history
InitFoxHoles(qubits);
ResetAll(qubits); // ALWAYS clean after yourself
}
return Zero;
}
// Inits fox holes, with almost equal probabilities
operation InitFoxHoles(register: Qubit[]) : Unit
{
body
{
ResetAll(register);
// Step 1
H(register[0]);
H(register[2]);
// Step 2
(Controlled (X))([register[0],register[2]], register[3]);
// Step 3
X(register[0]);
X(register[2]);
(Controlled (X))([register[0],register[2]], register[3]);
X(register[0]);
X(register[2]);
// Step 4
CNOT(register[3], register[0]);
CNOT(register[3], register[2]);
// Step 5
(Controlled (H))([register[3]], register[4]);
// Step 6
CNOT(register[4], register[3]);
}
}TestStrategy will test our strategy 1-2-3-1-2-3, InitFoxHoles () is responsible only for the initiation of fox holes. Let's check the initiation. Copy TestStrategy, start the initiation, measure the first 5 qubits and return their values.
operation TestInit(): (Result, Result, Result, Result, Result)
{
body
{
mutable res0 = Zero;
mutable res1 = Zero;
mutable res2 = Zero;
mutable res3 = Zero;
mutable res4 = Zero;
using(qubits=Qubit[16])
{
// 0..4 - holes
// 5 - current movement direction. Zero means "go down", One means "go up"
// 6 - Game status. 1 means "fox is free, go further"
// 7,8,9,10, 11 - movements history
InitFoxHoles(qubits);
set res0 = M(qubits[0]);
set res1 = M(qubits[1]);
set res2 = M(qubits[2]);
set res3 = M(qubits[3]);
set res4 = M(qubits[4]);
ResetAll(qubits); // ALWAYS clean after yourself
}
return (res0, res1, res2, res3, res4);
}
}We will run the test a thousand times (multiple runs are typical of quantum algorithms, in some places even necessary). Call code - under the spoiler, results: on the screen below.
Quickly test initiation
static void TestInitiation()
{
using (var sim = new QuantumSimulator())
{
var initedQubitsValues = Enumerable.Range(0, 5)
.ToDictionary(qubitIndex => qubitIndex, oneMesaured => 0);
for (int i = 0; i < 1000; i++)
{
(Result, Result, Result, Result, Result) result = TestInit.Run(sim).Result;
if (result.Item1 == Result.One) { initedQubitsValues[0]++; }
if (result.Item2 == Result.One) { initedQubitsValues[1]++; }
if (result.Item3 == Result.One) { initedQubitsValues[2]++; }
if (result.Item4 == Result.One) { initedQubitsValues[3]++; }
if (result.Item5 == Result.One) { initedQubitsValues[4]++; }
}
Console.WriteLine($"Qubit-0 initiations: {initedQubitsValues[0]}");
Console.WriteLine($"Qubit-1 initiations: {initedQubitsValues[1]}");
Console.WriteLine($"Qubit-2 initiations: {initedQubitsValues[2]}");
Console.WriteLine($"Qubit-3 initiations: {initedQubitsValues[3]}");
Console.WriteLine($"Qubit-4 initiations: {initedQubitsValues[4]}");
}
}
Something went wrong. An almost uniform distribution was expected. The reason is simple: in step 3, I inverted the third qubit, instead of the first: (Controlled (X)) ([register [0], register [2]], register [3]);
We fix the code, run the test:
Corrected Initiation
// Inits fox holes, with almost equal probabilities
operation InitFoxHoles(register: Qubit[]) : Unit
{
body
{
ResetAll(register);
// Step 1
H(register[0]);
H(register[2]);
// Step 2
(Controlled (X))([register[0],register[2]], register[3]);
// Step 3
X(register[0]);
X(register[2]);
(Controlled (X))([register[0],register[2]], register[1]);
X(register[0]);
X(register[2]);
// Step 4
CNOT(register[3], register[0]);
CNOT(register[3], register[2]);
// Step 5
(Controlled (H))([register[3]], register[4]);
// Step 6
CNOT(register[4], register[3]);
}
}
}
Already better. The code can be seen in the turnip, version Commit 1 .
Where to run the fox?
Select the fifth qubit (the numbering starts from above) under the current direction of the fox. We agree that zero means a downward movement, a unit means an upward movement. Obviously, if the fox is already in the zero hole - it should move down. If the fox is in the fourth hole, it moves up. In other cases, the fox can move up and down. According to these simple rules, we can set the “qubit of the current direction” to 0, 1, or a superposition of zero and one. We look at the code in the repository, Commit 2 .

Scheme in the editor.
Code and test

// Select next Fox movement direction, updating qubit 5
// 1 means go up (4 -> 3, 3 -> 2, ... 1 -> 0)
// 0 means go down (0 -> 1, 1 -> 2, ... 3 -> 4)
operation SetupMovementDirection(qubits: Qubit[]) : Unit
{
body
{
// Step 1
CNOT(qubits[4], qubits[5]);
// Step 2
(Controlled (H))([qubits[3]], qubits[5]);
// Step 3
(Controlled (H))([qubits[2]], qubits[5]);
// Step 4
(Controlled (H))([qubits[1]], qubits[5]);
}
}
operation TestMovementDirectionSetup(): (Result, Result, Result, Result, Result, Result)
{
body
{
mutable res0 = Zero;
mutable res1 = Zero;
mutable res2 = Zero;
mutable res3 = Zero;
mutable res4 = Zero;
mutable res5 = Zero;
using(qubits=Qubit[16])
{
InitFoxHoles(qubits);
SetupMovementDirection(qubits);
set res0 = M(qubits[0]);
set res1 = M(qubits[1]);
set res2 = M(qubits[2]);
set res3 = M(qubits[3]);
set res4 = M(qubits[4]);
set res5 = M(qubits[5]);
ResetAll(qubits); // ALWAYS clean after yourself
}
return (res0, res1, res2, res3, res4, res5);
}
} static void TestMovementDirectionSetup()
{
using (var sim = new QuantumSimulator())
{
List results = new List();
string initedCubit = null;
string moveDirection = null;
for (int i = 0; i < 1000; i++)
{
(Result, Result, Result, Result, Result, Result) result = Quantum.FoxHunter.TestMovementDirectionSetup.Run(sim).Result;
if (result.Item1 == Result.One) { initedCubit = "0"; }
if (result.Item2 == Result.One) { initedCubit = "1"; }
if (result.Item3 == Result.One) { initedCubit = "2"; }
if (result.Item4 == Result.One) { initedCubit = "3"; }
if (result.Item5 == Result.One) { initedCubit = "4"; }
if (result.Item6 == Result.One) { moveDirection = "1"; }
else { moveDirection = "0"; }
results.Add($"{initedCubit}{moveDirection}");
}
foreach(var group in results
.GroupBy(result => result)
.OrderBy(group => group.Key))
{
Console.WriteLine($"{group.Key} was measured {group.Count()} times");
}
Console.WriteLine($"\r\nTotal measures: {results.Count()}");
}
}

Traffic
Implemented by controlled SWAP. If the controlling qubit is single - swap down. If the controlling qubit is zero, we swap up.
Scheme in the editor .
Q # operator
// Makes a movement based on the 5'th qubit value
// 1 means go up (4 -> 3, 3 -> 2, ... 1 -> 0)
// 0 means go down (0 -> 1, 1 -> 2, ... 3 -> 4)
operation MakeMovement(qubits: Qubit[]) : Unit
{
body
{
// Code movement Up
// Step 1
mutable qubitsToSwap = [qubits[0], qubits[1]];
(Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap);
// Step 2
set qubitsToSwap = [qubits[1], qubits[2]];
(Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap);
// Step 3
set qubitsToSwap = [qubits[2], qubits[3]];
(Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap);
// Step 4
set qubitsToSwap = [qubits[3], qubits[4]];
(Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap);
// COde movement down
X(qubits[5]); // Invert direction qubit for the ZeroControlled operations
// Step 5
set qubitsToSwap = [qubits[3], qubits[4]];
(Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap);
// Step 6
set qubitsToSwap = [qubits[2], qubits[3]];
(Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap);
// Step 7
set qubitsToSwap = [qubits[1], qubits[2]];
(Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap);
// Step 8
set qubitsToSwap = [qubits[0], qubits[1]];
(Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap);
X(qubits[5]); // Back-invert for the direction qubit
}
}Q #: statement for tests
operation TestFirstMovement(): (Result, Result, Result, Result, Result, Result)
{
body
{
mutable res0 = Zero;
mutable res1 = Zero;
mutable res2 = Zero;
mutable res3 = Zero;
mutable res4 = Zero;
mutable res5 = Zero;
using(qubits=Qubit[16])
{
InitFoxHoles(qubits);
SetupMovementDirection(qubits);
MakeMovement(qubits);
set res0 = M(qubits[0]);
set res1 = M(qubits[1]);
set res2 = M(qubits[2]);
set res3 = M(qubits[3]);
set res4 = M(qubits[4]);
set res5 = M(qubits[5]);
ResetAll(qubits); // ALWAYS clean after yourself
}
return (res0, res1, res2, res3, res4, res5);
}
}C # code
static void TestFirstMove()
{
using (var sim = new QuantumSimulator())
{
List results = new List();
string initedCubit = null;
string moveDirection = null;
for (int i = 0; i < 1000; i++)
{
(Result, Result, Result, Result, Result, Result) result = Quantum.FoxHunter.TestFirstMovement.Run(sim).Result;
if (result.Item1 == Result.One) { initedCubit = "0"; }
if (result.Item2 == Result.One) { initedCubit = "1"; }
if (result.Item3 == Result.One) { initedCubit = "2"; }
if (result.Item4 == Result.One) { initedCubit = "3"; }
if (result.Item5 == Result.One) { initedCubit = "4"; }
if (result.Item6 == Result.One) { moveDirection = "1"; }
else { moveDirection = "0"; }
results.Add($"{initedCubit}{moveDirection}");
}
// Holes measurements
foreach (var group in results
.GroupBy(result => result[0])
.OrderBy(group => group.Key))
{
Console.WriteLine($"{group.Key} hole was measured {group.Count()} times");
}
// Directions measuremetns
foreach (var group in results
.GroupBy(result => result[1])
.OrderBy(group => group.Key))
{
Console.WriteLine($"{group.Key} direction was measured {group.Count()} times");
}
Console.WriteLine($"\r\nTotal measures: {results.Count()}");
}
} The code can be viewed in Commit 3 .
We make 6 moves
Finally, we select the sixth qubit for the status of the game (the fox is free / the fox is not free). The unit corresponds to a free fox. We will make further moves only with a single status qubit.
The qubits 7,8,9,10,11 will keep a history of moves. After each move, we are going to swap one of them with a qubit of the current direction (this will allow us to store the history of moves and reset the qubit of the current direction before each move).

Scheme attached .
Q # operator
/// Make 6 movements. Every movement is controlled by the 6'th qubit.
/// After the every qubit we check if the fox has been captured and invert the 6'th qubit
/// Reminder: 6'th qubit equal to One means "Fox is free, go further"
operation MakeSixMovements(qubits: Qubit[]) : Unit
{
body
{
// Move 1
(Controlled(SetupMovementDirection))([qubits[6]],(qubits));
(Controlled(MakeMovement))([qubits[6]],(qubits));
CNOT(qubits[1], qubits[6]); // Reverse Fox State if it's shot
// Move 2
SwapReverseRegister([qubits[5], qubits[7]]); // Move the first move direction to the qubit 7, qubit 5 is Zero again
(Controlled(SetupMovementDirection))([qubits[6]],(qubits));
(Controlled(MakeMovement))([qubits[6]],(qubits));
CNOT(qubits[2], qubits[6]);
// Move 3
SwapReverseRegister([qubits[5], qubits[8]]);
(Controlled(SetupMovementDirection))([qubits[6]],(qubits));
(Controlled(MakeMovement))([qubits[6]],(qubits));
CNOT(qubits[3], qubits[6]);
// Move 4
SwapReverseRegister([qubits[5], qubits[9]]);
(Controlled(SetupMovementDirection))([qubits[6]],(qubits));
(Controlled(MakeMovement))([qubits[6]],(qubits));
CNOT(qubits[1], qubits[6]);
// Move 5
SwapReverseRegister([qubits[5], qubits[10]]);
(Controlled(SetupMovementDirection))([qubits[6]],(qubits));
(Controlled(MakeMovement))([qubits[6]],(qubits));
CNOT(qubits[2], qubits[6]);
// Move 6
SwapReverseRegister([qubits[5], qubits[11]]);
(Controlled(SetupMovementDirection))([qubits[6]],(qubits));
(Controlled(MakeMovement))([qubits[6]],(qubits));
CNOT(qubits[3], qubits[6]);
}
}Q #: statement for tests
operation TestSixMovements(): (Result)
{
body
{
mutable res = Zero;
using(qubits=Qubit[16])
{
ResetAll(qubits);
InitFoxHoles(qubits);
X(qubits[6]); // At the beginning of the game our fox is alive
MakeSixMovements(qubits);
set res = M(qubits[6]);
ResetAll(qubits); // ALWAYS clean after yourself
}
return (res);
}
}C #: testing
static void TestMovements()
{
using (var sim = new QuantumSimulator())
{
int zerosCount = 0;
for (int i = 0; i < 1000; i++)
{
Result result = Quantum.FoxHunter.TestSixMovements.Run(sim).Result;
if(result == Result.Zero) { zerosCount++; }
}
Console.WriteLine($"\r\nTotal zeroes: {zerosCount}");
}
}We look Commit 4 .
Finishing touches
We have an error in the circuit. Since we test the strategy 1-2-3-1-2-3, we check each hole twice. Accordingly, having caught the fox on the first move, we will go through the status qubit twice (on the first move and fourth).
To avoid this situation, we use 12 qubits to fix the status after moves 4-5-6. In addition, we add the definition of victory: if at least one of the status qubits turns to zero, we won.

The final scheme .
Q #: fix the 6 move operator
operation MakeSixMovements(qubits: Qubit[]) : Unit
{
body
{
// Move 1
(Controlled(SetupMovementDirection))([qubits[6]],(qubits));
(Controlled(MakeMovement))([qubits[6]],(qubits));
CNOT(qubits[1], qubits[6]); // Reverse Fox State if it's shot
// Move 2
SwapReverseRegister([qubits[5], qubits[7]]); // Move the first move direction to the qubit 7, qubit 5 is Zero again
(Controlled(SetupMovementDirection))([qubits[6]],(qubits));
(Controlled(MakeMovement))([qubits[6]],(qubits));
CNOT(qubits[2], qubits[6]);
// Move 3
SwapReverseRegister([qubits[5], qubits[8]]);
(Controlled(SetupMovementDirection))([qubits[6]],(qubits));
(Controlled(MakeMovement))([qubits[6]],(qubits));
CNOT(qubits[3], qubits[6]);
// Move 4
SwapReverseRegister([qubits[5], qubits[9]]);
(Controlled(SetupMovementDirection))([qubits[6], qubits[12]],(qubits));
(Controlled(MakeMovement))([qubits[6], qubits[12]],(qubits));
CNOT(qubits[1], qubits[12]);
// Move 5
SwapReverseRegister([qubits[5], qubits[10]]);
(Controlled(SetupMovementDirection))([qubits[6], qubits[12]],(qubits));
(Controlled(MakeMovement))([qubits[6], qubits[12]],(qubits));
CNOT(qubits[2], qubits[12]);
// Move 6
SwapReverseRegister([qubits[5], qubits[11]]);
(Controlled(SetupMovementDirection))([qubits[6], qubits[12]],(qubits));
(Controlled(MakeMovement))([qubits[6], qubits[12]],(qubits));
CNOT(qubits[3], qubits[12]);
}
}Q #: fix operator testing strategy 1-2-3-1-2-3
operation TestStrategy () : (Result)
{
// 0..4 - holes
// 5 - current movement direction. Zero means "go down", One means "go up"
// 6 - Game status. 1 means "fox is free, go further"
// 7,8,9,10, 11 - movements history
// 12 - another qubit of the fox live. 1 means "fox is still free, go further"
// 13 Result qubit. If it's zero, the fox is alive
body
{
mutable res = Zero;
using(qubits=Qubit[14])
{
ResetAll(qubits);
// Init fox positions and the fox' live
InitFoxHoles(qubits);
X(qubits[6]); // At the beginning of the game our fox is alive
X(qubits[12]); // The second qubit of the fox live. If it's one - the fox is alive.
// Make moves
MakeSixMovements(qubits);
// Measure results. If the 13'th qubit is zero the fox is alive
X(qubits[6]);
X(qubits[12]);
CNOT(qubits[6], qubits[13]);
CNOT(qubits[12], qubits[13]);
CCNOT(qubits[6], qubits[12], qubits[13]);
set res = M(qubits[13]);
ResetAll(qubits); // ALWAYS clean after yourself
}
return (res);
}
}C #: run final check
static void RunFoxHunt()
{
Stopwatch sw = new Stopwatch();
sw.Start();
using (var sim = new QuantumSimulator())
{
var foxSurvives = 0;
var hunterWins = 0;
for (int i = 0; i < 1000; i++)
{
var result = (Result)(TestStrategy.Run(sim).Result);
if (result == Result.Zero) { foxSurvives++; }
else { hunterWins++; }
}
Console.WriteLine($"Fox survives: \t{foxSurvives}");
Console.WriteLine($"Hunter wins: \t{hunterWins}");
}
sw.Stop();
Console.WriteLine($"Experiment finished. " +
$"Time spent: {sw.ElapsedMilliseconds / 1000} seconds");
}
Commit 5 .
What follows from this
In principle, the scheme can be optimized both in the number of qubits and in the number of operations. The trivial optimization for the number of qubits is to get rid of qubit-13, returning only 6 and 12. Optimization for operations - to make the first shot immediately after initiation. However, let’s leave this work to Google engineers.
As you can see, anyone who is superficially familiar with quantum computing can safely play the "fox hunter." If we had a little more qubits, we could find the optimal solution, and not check the existing one. It is entirely possible that tic-tac-toe (and their quantum version), checkers, chess, Go will fall next.
At the same time, the issue of "solvability" of games like DotA, Starcraft and Doom remains open. For quantum computing, the storage of the entire history of clicks is characteristic. We take an APM (Actions Per Minute) of 500, multiply by the number of players, multiply by the number of minutes, add the randomness of the game itself - the number of qubits required to store all the information grows too quickly.
So, choosing a game in a small competition between Brin and Page can play a decisive role. However, the generation of a “equally difficult” game for classical and quantum computers deserves its own theory.
