Richard Hamming: Chapter 13. Information Theory
- Transfer
We did it!
 Hi, Habr. Remember the awesome article “You and Your Work” (+219, 2588 bookmarked, 429k reads)?
Hi, Habr. Remember the awesome article “You and Your Work” (+219, 2588 bookmarked, 429k reads)?
So Hamming (yes, yes, self-checking and self-correcting Hamming codes ) has a whole book written based on his lectures. We are translating it, because the man is talking business.
This book is not just about IT, it is a book about the thinking style of incredibly cool people. “This is not just a charge of positive thinking; it describes conditions that increase the chances of doing a great job. ”
Thanks for the translation to Andrei Pakhomov.
Information Theory was developed by C.E. Shannon in the late 1940s. Bell Labs management insisted that he call it “Communication Theory,” because this is a much more accurate name. For obvious reasons, the name "Information Theory" has a significantly greater impact on the public, so Shannon chose it, and it is what we know to this day. The name itself suggests that the theory deals with information, which makes it important, since we are penetrating deeper into the information age. In this chapter, I will touch on a few basic conclusions from this theory, I will give not strict, but rather intuitive evidence of some of the separate provisions of this theory, so that you understand what the "Information Theory" is in fact, where you can apply it and where not .
First of all, what is “information”? Shannon identifies information with uncertainty. He chose the negative logarithm of the probability of an event as a quantitative measure of the information that you receive when an event occurs with probability p. For example, if I tell you that the weather in Los Angeles is foggy, then p is close to 1, which by and large does not give us much information. But if I say that it rains in Monterey in June, then there will be uncertainty in this message, and it will contain more information. A reliable event does not contain any information, since log 1 = 0.
Let us dwell on this in more detail. Shannon believed that a quantitative measure of information should be a continuous function of the probability of an event p, and for independent events it should be additive - the amount of information obtained as a result of two independent events should be equal to the amount of information obtained as a result of a joint event. For example, the result of a roll of dice and coins is usually regarded as independent events. Let us translate the above into the language of mathematics. If I (p) is the amount of information that is contained in an event with probability p, then for a joint event consisting of two independent events x with probability p 1 and y with probability p 2 we obtain

(x and y independent events)
This is the functional Cauchy equation, true for all p 1 and p2. To solve this functional equation, suppose that
p 1 = p 2 = p,
this gives

If p 1 = p 2 and p 2 = p, then

etc. Extending this process using the standard method for exponentials for all rational numbers m / n, the following is true.

From the assumed continuity of the information measure, it follows that the logarithmic function is the only continuous solution to the Cauchy functional equation.
In the theory of information, it is customary to take the base of the logarithm of 2, so the binary choice contains exactly 1 bit of information. Therefore, information is measured by the formula.

Let's pause and see what happened above. First of all, we did not give a definition to the concept of “information”, we just defined a formula for its quantitative measure.
Secondly, this measure depends on the uncertainty, and although it is sufficiently suitable for machines - for example, telephone systems, radio, television, computers, etc. - it does not reflect a normal human attitude to information.
Thirdly, this is a relative measure, it depends on the current state of your knowledge. If you look at the stream of “random numbers” from the random number generator, you assume that each next number is indefinite, but if you know the formula for calculating “random numbers”, the next number will be known and, accordingly, will not contain information.
Thus, the definition given by Shannon for information is in many cases suitable for machines, but does not seem to correspond to the human understanding of the word. For this reason, the “Information Theory” should be called the “Communication Theory.” However, it’s too late to change the definitions (thanks to which the theory has gained its initial popularity, and which still make people think that this theory deals with “information”), so we have to put up with them, but you have to clearly understand how far the definition of information given by Shannon is far from its common sense. Shannon’s information deals with something completely different, namely uncertainty.
This is what you need to think about when you offer any terminology. How consistent is the proposed definition, for example, the definition given by Shannon, with your original idea, and how different is it? There is almost no term that would accurately reflect your earlier vision of the concept, but in the end, it is the terminology used that reflects the meaning of the concept, so formalizing something through clear definitions always makes some noise.
Consider a system whose alphabet consists of symbols q with probabilities pi. In this case, the average amount of information in the system (its expected value) is:
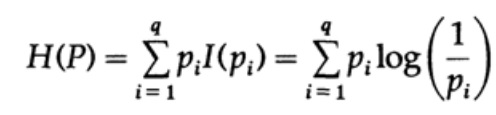
This is called the entropy of the probability distribution system {pi}. We use the term “entropy” because the same mathematical form arises in thermodynamics and statistical mechanics. That is why the term "entropy" creates around itself an aura of importance, which, ultimately, is not justified. The same mathematical form of notation does not imply the same interpretation of characters!
The entropy of the probability distribution plays a major role in coding theory. Gibbs inequality for two different probability distributions pi and qi is one of the important consequences of this theory. So, we must prove that the
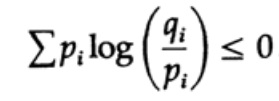
proof is based on an obvious graph, fig. 13.I, which shows that
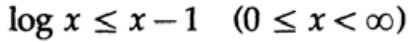
and equality is achieved only for x = 1. We apply the inequality to each summand of the sum from the left side:

If the communication system alphabet consists of q characters, then taking the probability of transmission of each character qi = 1 / q and substituting q, we get from Gibbs inequality


Figure 13. I
This suggests that if the probability of transmitting all q characters is the same and equal to - 1 / q, then the maximum entropy is ln q, otherwise the inequality holds.
In the case of a uniquely decoded code, we have the Kraft inequality.
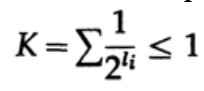
Now if we define pseudo-probabilities

where of course = 1, which follows from the Gibbs inequality,
= 1, which follows from the Gibbs inequality,

and apply some algebra (remember that K ≤ 1, so we can omit the logarithmic term, and possibly strengthen the inequality later), we get

where L is the average length of the code.
Thus, entropy is the minimum boundary for any character code with an average codeword L. This is Shannon's theorem for a channel without interference.
Now we consider the main theorem on the limitations of communication systems in which information is transmitted in the form of a stream of independent bits and noise is present. It is assumed that the probability of the correct transmission of one bit is P> 1/2, and the probability that the bit value will be inverted during transmission (an error occurs) is Q = 1 - P. For convenience, we assume that the errors are independent and the probability of error is the same for each sent bits - that is, there is “white noise” in the communication channel.
The way we have a long stream of n bits encoded in a single message is an n-dimensional extension of a one-bit code. We will determine the value of n later. Consider a message consisting of n-bits as a point in n-dimensional space. Since we have n-dimensional space - and for simplicity we assume that each message has the same probability of occurrence - there are M possible messages (M will also be determined later), therefore, the probability of any sent message is equal to
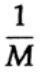

(sender)
Figure 13.II
Next, consider the idea of channel bandwidth. Without going into details, the channel capacity is defined as the maximum amount of information that can be reliably transmitted over the communication channel, taking into account the use of the most efficient encoding. There is no argument that more information can be transmitted through the communication channel than its capacity. This can be proved for a binary symmetric channel (which we use in our case). The channel capacity, when sending bitwise, is specified as
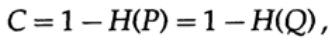
where, as before, P is the probability of an error in any sent bit. When sending n independent bits, the channel capacity is determined as
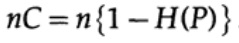
If we are close to the bandwidth of the channel, then we should send almost such a volume of information for each of the characters ai, i = 1, ..., M. Given that the probability of occurrence of each character ai is 1 / M, we get
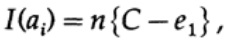
when we send any of M equally probable messages ai, we have

When sending n bits we expect nQ errors to occur. In practice, for a message consisting of n-bits, we will have approximately nQ errors in the received message. For large n, the relative variation (variation = distribution width,) of the
distribution of the number of errors will be narrower with increasing n.
So, from the side of the transmitter, I take the ai message to send and draw a sphere around it with a radius

which is slightly larger by an amount equal to e2 than the expected number of errors Q, (Figure 13.II). If n is large enough, then there is an arbitrarily small probability of the appearance of the message point bj on the receiver side, which goes beyond this sphere. We will draw the situation, as I see it from the point of view of the transmitter: we have any radii from the transmitted message ai to the received message bj with a probability of error equal to (or almost equal to) the normal distribution, reaching a maximum in nQ. For any given e2, there is n so large that the probability that the resulting point bj, going beyond my sphere, will be as small as you please.
Now consider the same situation on your part (Fig. 13.III). On the receiver side there is a sphere S (r) of the same radius r around the received point bj in n-dimensional space, such that if the received message bj is inside my sphere, then the message ai I sent is inside your sphere.
How can an error occur? An error can occur in the cases described in the table below:

Figure 13.III

Here we see that if in the sphere constructed around the received point there is at least one more point corresponding to a possible sent unencoded message, then an error occurred during transmission, since you cannot determine which of these messages was transmitted. The sent message does not contain errors only if the point corresponding to it is in the sphere, and there are no other points that are possible in this code that are in the same sphere.
We have a mathematical equation for the error probability Re, if the message ai was sent.

We can throw out the first factor in the second term, taking it as 1. Thus, we obtain the inequality

Obviously,

therefore , we
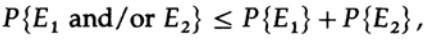
repeatedly apply to the last term on the right
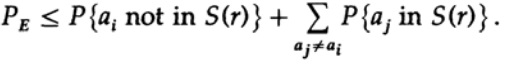
If n is taken large enough, the first term can be taken arbitrarily small, say, less than a certain number d. Therefore, we have
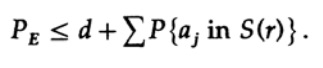
Now consider how to construct a simple replacement code for encoding M messages consisting of n bits. Having no idea how to build the code (error correction codes have not yet been invented), Shannon chose random coding. Flip a coin for each of the n bits in the message and repeat the process for M messages. All you need to do is nM coin toss, so it’s possible

code dictionaries having the same probability of ½nM. Of course, the random process of creating a codebook means that there is a likelihood of duplicates, as well as code points, which will be close to each other and, therefore, will be a source of probable errors. It is necessary to prove that if this does not happen with a probability higher than any small selected level of error, then the given n is large enough.
The decisive point is that Shannon averaged all possible code books to find the average error! We will use the Av [.] Symbol to denote the average over the set of all possible random code dictionaries. Averaging over the constant d, of course, gives a constant, since for averaging each term coincides with any other term in the sum
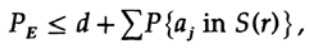
which can be increased (M – 1 goes to M)
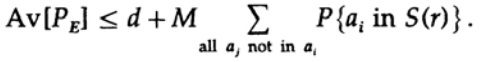
For any particular message, when averaging all code books, coding runs through all possible values, so the average probability that a point is in a sphere is the ratio of the volume of the sphere to the total amount of space. In this case, the volume of the sphere is

where s = Q + e2 <1/2 and ns must be an integer.
The last term on the right is the largest in this sum. First, we estimate its value by the Stirling formula for factorials. Then we look at the coefficient of reduction of the term in front of it, note that this coefficient increases when moving to the left, and therefore we can: (1) limit the value of the sum to the sum of the geometric progression with this initial coefficient, (2) expand the geometric progression from ns members to infinite number of terms, (3) calculate the sum of infinite geometric progression (standard algebra, nothing significant) and finally get the limit value (for a sufficiently large n):

Notice how the entropy H (s) appeared in the binomial identity. Note that the expansion in the Taylor series H (s) = H (Q + e2) gives an estimate obtained taking into account only the first derivative and ignoring all the others. Now we collect the final expression:
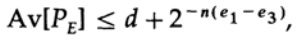
where

All we need to do is choose e2 so that e3 <e1, and then the last term will be arbitrarily small, for n sufficiently large. Therefore, the average PE error can be obtained arbitrarily small with a channel capacity arbitrarily close to C.
If the average of all codes has a sufficiently small error, then at least one code must be suitable, therefore, at least one suitable coding system exists. This is an important result obtained by Shannon - “Shannon's theorem for a channel with interference”, although it should be noted that he proved it for a much more general case than for a simple binary symmetric channel that I used. For the general case, mathematical calculations are much more complicated, but the ideas are not so different, so very often, using the example of a special case, one can reveal the true meaning of the theorem.
Let's criticize the result. We repeatedly repeated: "For sufficiently large n." But how big is n? Very, very large, if you really want to be simultaneously close to the bandwidth of the channel and be sure of the correct data transfer! So big that in fact you will have to wait a very long time to accumulate a message from so many bits in order to encode it later. At the same time, the size of the random code dictionary will be huge (after all, such a dictionary cannot be represented in a shorter form than the complete list of all Mn bits, while n and M are very large)!
Error correction codes avoid waiting for a very long message, with its subsequent encoding and decoding through very large codebooks, because they avoid codebooks per se and use conventional calculations instead. In a simple theory, such codes, as a rule, lose their ability to approach the channel capacity and at the same time maintain a fairly low error rate, but when the code corrects a large number of errors, they show good results. In other words, if you are laying some kind of channel capacity for error correction, then you should use the error correction option most of the time, i.e., a large number of errors should be fixed in each sent message, otherwise you will lose this capacity for nothing.
Moreover, the theorem proved above is still not meaningless! It shows that efficient transmission systems should use sophisticated coding schemes for very long bit strings. An example is satellites that have flown outside the outer planet; as they move away from the Earth and the Sun, they are forced to correct more and more errors in the data block: some satellites use solar panels, which give about 5 watts, others use atomic power sources that give about the same power. The weak power of the power source, the small size of the transmitter plates and the limited size of the receiver plates on Earth, the huge distance that the signal must cover - all this requires the use of codes with a high level of error correction to build an effective communication system.
We return to the n-dimensional space that we used in the proof above. Discussing it, we showed that almost the entire volume of the sphere is concentrated near the outer surface, - thus, almost certainly the sent signal will be located at the surface of the sphere built around the received signal, even with a relatively small radius of such a sphere. Therefore, it is not surprising that the received signal after correction of an arbitrarily large number of errors, nQ, turns out to be arbitrarily close to the signal without errors. The capacity of the communication channel, which we examined earlier, is the key to understanding this phenomenon. Please note that such spheres constructed for Hamming error correction codes do not overlap. A large number of practically orthogonal measurements in n-dimensional space show why can we fit M spheres in a space with a slight overlap. If you allow a small, arbitrarily small overlap, which can lead only to a small number of errors during decoding, you can get a dense arrangement of spheres in space. Hamming guaranteed a certain level of error correction, Shannon - a low probability of error, but at the same time maintaining the actual bandwidth arbitrarily close to the capacity of the communication channel, which Hamming codes can not do.
Information theory does not talk about how to design an effective system, but it indicates the direction of movement toward effective communication systems. This is a valuable tool for building communication systems between machines, but, as noted earlier, it does not have much to do with how people exchange information with each other. The extent to which biological inheritance is similar to technical communication systems is simply unknown, so it is currently not clear how information theory applies to genes. We have no choice but to try, and if success shows us the machine-like nature of this phenomenon, then failure will point to other significant aspects of the nature of information.
Let's not get distracted much. We have seen that all initial definitions, to a greater or lesser extent, should express the essence of our initial beliefs, but they are characterized by a certain degree of distortion, and therefore they are not applicable. It is traditionally accepted that, ultimately, the definition that we use actually defines the essence; but, it only tells us how to process things and in no way makes us any sense. The postulative approach, so strongly acclaimed in mathematical circles, leaves much to be desired in practice.
Now we will look at an example of IQ tests, where the definition is as cyclical as you like, and as a result misleads you. A test is created that is supposed to measure intelligence. After that, it is reviewed to be as consistent as possible, and then it is published and calibrated in a simple way so that the measured "intelligence" is normally distributed (of course, along the calibration curve). All definitions should be cross-checked, not only when they are first proposed, but much later, when they are used in the conclusions made. To what extent are the definition boundaries suitable for the task at hand? How often do the definitions given in the same conditions begin to be applied in quite different conditions? This is common enough!
Thus, one of the goals of this presentation of information theory, in addition to demonstrating its usefulness, was to warn you about this danger, or to demonstrate how to use it to obtain the desired result. It has long been noticed that the initial definitions determine what you find in the end, to a much greater extent than it seems. Initial definitions require you to pay great attention not only in any new situation, but also in areas with which you have been working for a long time. This will allow you to understand to what extent the results obtained are a tautology, and not something useful.
Eddington's famous story tells of people who fished in the sea with a net. After examining the size of the fish they caught, they determined the minimum size of fish that live in the sea! Their conclusion was due to the tool used, and not reality.
To be continued ...
Who wants to help with the translation, layout and publication of a book - write in a personal or mail magisterludi2016@yandex.ru
By the way, we have launched a translation of another book coolest - «of The Dream Machine: The history of the computer revolution" )
is especially looking for those who will help translate the bonus chapter, which is only on the video . ( translate 10 minutes, the first 20 have already taken )
“The goal of this course is to prepare you for your technical future.”
 Hi, Habr. Remember the awesome article “You and Your Work” (+219, 2588 bookmarked, 429k reads)?
Hi, Habr. Remember the awesome article “You and Your Work” (+219, 2588 bookmarked, 429k reads)? So Hamming (yes, yes, self-checking and self-correcting Hamming codes ) has a whole book written based on his lectures. We are translating it, because the man is talking business.
This book is not just about IT, it is a book about the thinking style of incredibly cool people. “This is not just a charge of positive thinking; it describes conditions that increase the chances of doing a great job. ”
Thanks for the translation to Andrei Pakhomov.
Information Theory was developed by C.E. Shannon in the late 1940s. Bell Labs management insisted that he call it “Communication Theory,” because this is a much more accurate name. For obvious reasons, the name "Information Theory" has a significantly greater impact on the public, so Shannon chose it, and it is what we know to this day. The name itself suggests that the theory deals with information, which makes it important, since we are penetrating deeper into the information age. In this chapter, I will touch on a few basic conclusions from this theory, I will give not strict, but rather intuitive evidence of some of the separate provisions of this theory, so that you understand what the "Information Theory" is in fact, where you can apply it and where not .
First of all, what is “information”? Shannon identifies information with uncertainty. He chose the negative logarithm of the probability of an event as a quantitative measure of the information that you receive when an event occurs with probability p. For example, if I tell you that the weather in Los Angeles is foggy, then p is close to 1, which by and large does not give us much information. But if I say that it rains in Monterey in June, then there will be uncertainty in this message, and it will contain more information. A reliable event does not contain any information, since log 1 = 0.
Let us dwell on this in more detail. Shannon believed that a quantitative measure of information should be a continuous function of the probability of an event p, and for independent events it should be additive - the amount of information obtained as a result of two independent events should be equal to the amount of information obtained as a result of a joint event. For example, the result of a roll of dice and coins is usually regarded as independent events. Let us translate the above into the language of mathematics. If I (p) is the amount of information that is contained in an event with probability p, then for a joint event consisting of two independent events x with probability p 1 and y with probability p 2 we obtain

(x and y independent events)
This is the functional Cauchy equation, true for all p 1 and p2. To solve this functional equation, suppose that
p 1 = p 2 = p,
this gives

If p 1 = p 2 and p 2 = p, then

etc. Extending this process using the standard method for exponentials for all rational numbers m / n, the following is true.

From the assumed continuity of the information measure, it follows that the logarithmic function is the only continuous solution to the Cauchy functional equation.
In the theory of information, it is customary to take the base of the logarithm of 2, so the binary choice contains exactly 1 bit of information. Therefore, information is measured by the formula.

Let's pause and see what happened above. First of all, we did not give a definition to the concept of “information”, we just defined a formula for its quantitative measure.
Secondly, this measure depends on the uncertainty, and although it is sufficiently suitable for machines - for example, telephone systems, radio, television, computers, etc. - it does not reflect a normal human attitude to information.
Thirdly, this is a relative measure, it depends on the current state of your knowledge. If you look at the stream of “random numbers” from the random number generator, you assume that each next number is indefinite, but if you know the formula for calculating “random numbers”, the next number will be known and, accordingly, will not contain information.
Thus, the definition given by Shannon for information is in many cases suitable for machines, but does not seem to correspond to the human understanding of the word. For this reason, the “Information Theory” should be called the “Communication Theory.” However, it’s too late to change the definitions (thanks to which the theory has gained its initial popularity, and which still make people think that this theory deals with “information”), so we have to put up with them, but you have to clearly understand how far the definition of information given by Shannon is far from its common sense. Shannon’s information deals with something completely different, namely uncertainty.
This is what you need to think about when you offer any terminology. How consistent is the proposed definition, for example, the definition given by Shannon, with your original idea, and how different is it? There is almost no term that would accurately reflect your earlier vision of the concept, but in the end, it is the terminology used that reflects the meaning of the concept, so formalizing something through clear definitions always makes some noise.
Consider a system whose alphabet consists of symbols q with probabilities pi. In this case, the average amount of information in the system (its expected value) is:
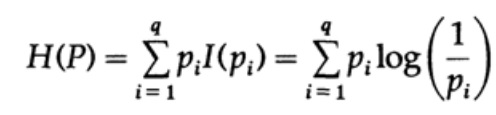
This is called the entropy of the probability distribution system {pi}. We use the term “entropy” because the same mathematical form arises in thermodynamics and statistical mechanics. That is why the term "entropy" creates around itself an aura of importance, which, ultimately, is not justified. The same mathematical form of notation does not imply the same interpretation of characters!
The entropy of the probability distribution plays a major role in coding theory. Gibbs inequality for two different probability distributions pi and qi is one of the important consequences of this theory. So, we must prove that the
proof is based on an obvious graph, fig. 13.I, which shows that
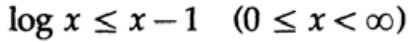
and equality is achieved only for x = 1. We apply the inequality to each summand of the sum from the left side:

If the communication system alphabet consists of q characters, then taking the probability of transmission of each character qi = 1 / q and substituting q, we get from Gibbs inequality


Figure 13. I
This suggests that if the probability of transmitting all q characters is the same and equal to - 1 / q, then the maximum entropy is ln q, otherwise the inequality holds.
In the case of a uniquely decoded code, we have the Kraft inequality.
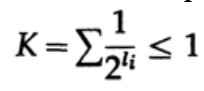
Now if we define pseudo-probabilities

where of course
 = 1, which follows from the Gibbs inequality,
= 1, which follows from the Gibbs inequality,
and apply some algebra (remember that K ≤ 1, so we can omit the logarithmic term, and possibly strengthen the inequality later), we get

where L is the average length of the code.
Thus, entropy is the minimum boundary for any character code with an average codeword L. This is Shannon's theorem for a channel without interference.
Now we consider the main theorem on the limitations of communication systems in which information is transmitted in the form of a stream of independent bits and noise is present. It is assumed that the probability of the correct transmission of one bit is P> 1/2, and the probability that the bit value will be inverted during transmission (an error occurs) is Q = 1 - P. For convenience, we assume that the errors are independent and the probability of error is the same for each sent bits - that is, there is “white noise” in the communication channel.
The way we have a long stream of n bits encoded in a single message is an n-dimensional extension of a one-bit code. We will determine the value of n later. Consider a message consisting of n-bits as a point in n-dimensional space. Since we have n-dimensional space - and for simplicity we assume that each message has the same probability of occurrence - there are M possible messages (M will also be determined later), therefore, the probability of any sent message is equal to
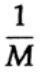

(sender)
Figure 13.II
Next, consider the idea of channel bandwidth. Without going into details, the channel capacity is defined as the maximum amount of information that can be reliably transmitted over the communication channel, taking into account the use of the most efficient encoding. There is no argument that more information can be transmitted through the communication channel than its capacity. This can be proved for a binary symmetric channel (which we use in our case). The channel capacity, when sending bitwise, is specified as
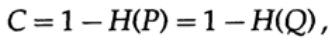
where, as before, P is the probability of an error in any sent bit. When sending n independent bits, the channel capacity is determined as
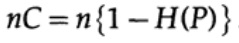
If we are close to the bandwidth of the channel, then we should send almost such a volume of information for each of the characters ai, i = 1, ..., M. Given that the probability of occurrence of each character ai is 1 / M, we get
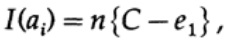
when we send any of M equally probable messages ai, we have

When sending n bits we expect nQ errors to occur. In practice, for a message consisting of n-bits, we will have approximately nQ errors in the received message. For large n, the relative variation (variation = distribution width,) of the
distribution of the number of errors will be narrower with increasing n.
So, from the side of the transmitter, I take the ai message to send and draw a sphere around it with a radius

which is slightly larger by an amount equal to e2 than the expected number of errors Q, (Figure 13.II). If n is large enough, then there is an arbitrarily small probability of the appearance of the message point bj on the receiver side, which goes beyond this sphere. We will draw the situation, as I see it from the point of view of the transmitter: we have any radii from the transmitted message ai to the received message bj with a probability of error equal to (or almost equal to) the normal distribution, reaching a maximum in nQ. For any given e2, there is n so large that the probability that the resulting point bj, going beyond my sphere, will be as small as you please.
Now consider the same situation on your part (Fig. 13.III). On the receiver side there is a sphere S (r) of the same radius r around the received point bj in n-dimensional space, such that if the received message bj is inside my sphere, then the message ai I sent is inside your sphere.
How can an error occur? An error can occur in the cases described in the table below:

Figure 13.III

Here we see that if in the sphere constructed around the received point there is at least one more point corresponding to a possible sent unencoded message, then an error occurred during transmission, since you cannot determine which of these messages was transmitted. The sent message does not contain errors only if the point corresponding to it is in the sphere, and there are no other points that are possible in this code that are in the same sphere.
We have a mathematical equation for the error probability Re, if the message ai was sent.

We can throw out the first factor in the second term, taking it as 1. Thus, we obtain the inequality

Obviously,

therefore , we
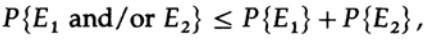
repeatedly apply to the last term on the right
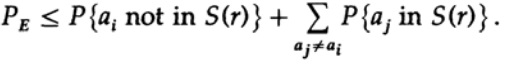
If n is taken large enough, the first term can be taken arbitrarily small, say, less than a certain number d. Therefore, we have
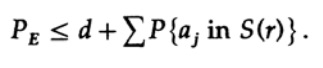
Now consider how to construct a simple replacement code for encoding M messages consisting of n bits. Having no idea how to build the code (error correction codes have not yet been invented), Shannon chose random coding. Flip a coin for each of the n bits in the message and repeat the process for M messages. All you need to do is nM coin toss, so it’s possible

code dictionaries having the same probability of ½nM. Of course, the random process of creating a codebook means that there is a likelihood of duplicates, as well as code points, which will be close to each other and, therefore, will be a source of probable errors. It is necessary to prove that if this does not happen with a probability higher than any small selected level of error, then the given n is large enough.
The decisive point is that Shannon averaged all possible code books to find the average error! We will use the Av [.] Symbol to denote the average over the set of all possible random code dictionaries. Averaging over the constant d, of course, gives a constant, since for averaging each term coincides with any other term in the sum
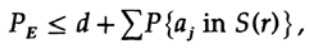
which can be increased (M – 1 goes to M)
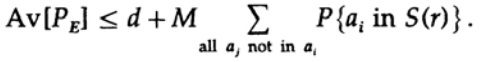
For any particular message, when averaging all code books, coding runs through all possible values, so the average probability that a point is in a sphere is the ratio of the volume of the sphere to the total amount of space. In this case, the volume of the sphere is

where s = Q + e2 <1/2 and ns must be an integer.
The last term on the right is the largest in this sum. First, we estimate its value by the Stirling formula for factorials. Then we look at the coefficient of reduction of the term in front of it, note that this coefficient increases when moving to the left, and therefore we can: (1) limit the value of the sum to the sum of the geometric progression with this initial coefficient, (2) expand the geometric progression from ns members to infinite number of terms, (3) calculate the sum of infinite geometric progression (standard algebra, nothing significant) and finally get the limit value (for a sufficiently large n):

Notice how the entropy H (s) appeared in the binomial identity. Note that the expansion in the Taylor series H (s) = H (Q + e2) gives an estimate obtained taking into account only the first derivative and ignoring all the others. Now we collect the final expression:
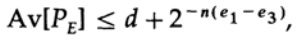
where

All we need to do is choose e2 so that e3 <e1, and then the last term will be arbitrarily small, for n sufficiently large. Therefore, the average PE error can be obtained arbitrarily small with a channel capacity arbitrarily close to C.
If the average of all codes has a sufficiently small error, then at least one code must be suitable, therefore, at least one suitable coding system exists. This is an important result obtained by Shannon - “Shannon's theorem for a channel with interference”, although it should be noted that he proved it for a much more general case than for a simple binary symmetric channel that I used. For the general case, mathematical calculations are much more complicated, but the ideas are not so different, so very often, using the example of a special case, one can reveal the true meaning of the theorem.
Let's criticize the result. We repeatedly repeated: "For sufficiently large n." But how big is n? Very, very large, if you really want to be simultaneously close to the bandwidth of the channel and be sure of the correct data transfer! So big that in fact you will have to wait a very long time to accumulate a message from so many bits in order to encode it later. At the same time, the size of the random code dictionary will be huge (after all, such a dictionary cannot be represented in a shorter form than the complete list of all Mn bits, while n and M are very large)!
Error correction codes avoid waiting for a very long message, with its subsequent encoding and decoding through very large codebooks, because they avoid codebooks per se and use conventional calculations instead. In a simple theory, such codes, as a rule, lose their ability to approach the channel capacity and at the same time maintain a fairly low error rate, but when the code corrects a large number of errors, they show good results. In other words, if you are laying some kind of channel capacity for error correction, then you should use the error correction option most of the time, i.e., a large number of errors should be fixed in each sent message, otherwise you will lose this capacity for nothing.
Moreover, the theorem proved above is still not meaningless! It shows that efficient transmission systems should use sophisticated coding schemes for very long bit strings. An example is satellites that have flown outside the outer planet; as they move away from the Earth and the Sun, they are forced to correct more and more errors in the data block: some satellites use solar panels, which give about 5 watts, others use atomic power sources that give about the same power. The weak power of the power source, the small size of the transmitter plates and the limited size of the receiver plates on Earth, the huge distance that the signal must cover - all this requires the use of codes with a high level of error correction to build an effective communication system.
We return to the n-dimensional space that we used in the proof above. Discussing it, we showed that almost the entire volume of the sphere is concentrated near the outer surface, - thus, almost certainly the sent signal will be located at the surface of the sphere built around the received signal, even with a relatively small radius of such a sphere. Therefore, it is not surprising that the received signal after correction of an arbitrarily large number of errors, nQ, turns out to be arbitrarily close to the signal without errors. The capacity of the communication channel, which we examined earlier, is the key to understanding this phenomenon. Please note that such spheres constructed for Hamming error correction codes do not overlap. A large number of practically orthogonal measurements in n-dimensional space show why can we fit M spheres in a space with a slight overlap. If you allow a small, arbitrarily small overlap, which can lead only to a small number of errors during decoding, you can get a dense arrangement of spheres in space. Hamming guaranteed a certain level of error correction, Shannon - a low probability of error, but at the same time maintaining the actual bandwidth arbitrarily close to the capacity of the communication channel, which Hamming codes can not do.
Information theory does not talk about how to design an effective system, but it indicates the direction of movement toward effective communication systems. This is a valuable tool for building communication systems between machines, but, as noted earlier, it does not have much to do with how people exchange information with each other. The extent to which biological inheritance is similar to technical communication systems is simply unknown, so it is currently not clear how information theory applies to genes. We have no choice but to try, and if success shows us the machine-like nature of this phenomenon, then failure will point to other significant aspects of the nature of information.
Let's not get distracted much. We have seen that all initial definitions, to a greater or lesser extent, should express the essence of our initial beliefs, but they are characterized by a certain degree of distortion, and therefore they are not applicable. It is traditionally accepted that, ultimately, the definition that we use actually defines the essence; but, it only tells us how to process things and in no way makes us any sense. The postulative approach, so strongly acclaimed in mathematical circles, leaves much to be desired in practice.
Now we will look at an example of IQ tests, where the definition is as cyclical as you like, and as a result misleads you. A test is created that is supposed to measure intelligence. After that, it is reviewed to be as consistent as possible, and then it is published and calibrated in a simple way so that the measured "intelligence" is normally distributed (of course, along the calibration curve). All definitions should be cross-checked, not only when they are first proposed, but much later, when they are used in the conclusions made. To what extent are the definition boundaries suitable for the task at hand? How often do the definitions given in the same conditions begin to be applied in quite different conditions? This is common enough!
Thus, one of the goals of this presentation of information theory, in addition to demonstrating its usefulness, was to warn you about this danger, or to demonstrate how to use it to obtain the desired result. It has long been noticed that the initial definitions determine what you find in the end, to a much greater extent than it seems. Initial definitions require you to pay great attention not only in any new situation, but also in areas with which you have been working for a long time. This will allow you to understand to what extent the results obtained are a tautology, and not something useful.
Eddington's famous story tells of people who fished in the sea with a net. After examining the size of the fish they caught, they determined the minimum size of fish that live in the sea! Their conclusion was due to the tool used, and not reality.
To be continued ...
Who wants to help with the translation, layout and publication of a book - write in a personal or mail magisterludi2016@yandex.ru
By the way, we have launched a translation of another book coolest - «of The Dream Machine: The history of the computer revolution" )
is especially looking for those who will help translate the bonus chapter, which is only on the video . ( translate 10 minutes, the first 20 have already taken )
Book Contents and Translated Chapters
Foreword
Who wants to help with the translation, layout and publication of the book - write in a personal email or mail magisterludi2016@yandex.ru
- Intro to The Art of Doing Science and Engineering: Learning to Learn (March 28, 1995) Translation: Chapter 1
- “Foundations of the Digital (Discrete) Revolution” (March 30, 1995) Chapter 2. Fundamentals of the Digital (Discrete) Revolution
- “History of Computers - Hardware” (March 31, 1995) Chapter 3. Computer History - Hardware
- “History of Computers - Software” (April 4, 1995) Chapter 4. History of Computers - Software
- History of Computers - Applications (April 6, 1995) Chapter 5. Computer History - Practical Application
- “Artificial Intelligence - Part I” (April 7, 1995) Chapter 6. Artificial Intelligence - 1
- “Artificial Intelligence - Part II” (April 11, 1995) Chapter 7. Artificial Intelligence - II
- “Artificial Intelligence III” (April 13, 1995) Chapter 8. Artificial Intelligence-III
- “N-Dimensional Space” (April 14, 1995) Chapter 9. N-Dimensional Space
- “Coding Theory - The Representation of Information, Part I” (April 18, 1995) Chapter 10. Coding Theory - I
- “Coding Theory - The Representation of Information, Part II” (April 20, 1995) Chapter 11. Coding Theory - II
- “Error-Correcting Codes” (April 21, 1995) Chapter 12. Error Correction Codes
- Information Theory (April 25, 1995) Chapter 13. Information Theory
- Digital Filters, Part I (April 27, 1995) Chapter 14. Digital Filters - 1
- Digital Filters, Part II (April 28, 1995) Chapter 15. Digital Filters - 2
- Digital Filters, Part III (May 2, 1995) Chapter 16. Digital Filters - 3
- Digital Filters, Part IV (May 4, 1995) Chapter 17. Digital Filters - IV
- “Simulation, Part I” (May 5, 1995) Chapter 18. Modeling - I
- “Simulation, Part II” (May 9, 1995) Chapter 19. Modeling - II
- “Simulation, Part III” (May 11, 1995) Chapter 20. Modeling - III
- Fiber Optics (May 12, 1995) Chapter 21. Fiber Optics
- Computer Aided Instruction (May 16, 1995) Chapter 22. Computer-Aided Learning (CAI)
- Mathematics (May 18, 1995) Chapter 23. Mathematics
- Quantum Mechanics (May 19, 1995) Chapter 24. Quantum Mechanics
- Creativity (May 23, 1995). Translation: Chapter 25. Creativity
- “Experts” (May 25, 1995) Chapter 26. Experts
- “Unreliable Data” (May 26, 1995) Chapter 27. Invalid Data
- Systems Engineering (May 30, 1995) Chapter 28. Systems Engineering
- “You Get What You Measure” (June 1, 1995) Chapter 29. You Get What You Measure
- “How Do We Know What We Know” (June 2, 1995) translate in 10 minute slices
- Hamming, “You and Your Research” (June 6, 1995). Translation: You and Your Work
Who wants to help with the translation, layout and publication of the book - write in a personal email or mail magisterludi2016@yandex.ru
