Probability in quantum mechanics. Where did it come from and how to simplify it for understanding

Introduction

This article is intended for people who have an initial knowledge of quantum mechanics, which is usually part of the university course in theoretical physics, as well as a keen interest in it. Quantum mechanics, like matanalysis, requires certain initial knowledge, and without it, any reading will either be fiction or lead to misconceptions. All the promises of quantum mechanics are for everyone a gift akin to socialist election slogans. Nevertheless, this necessary knowledge is not as great as it might seem, especially for those who know mathematics. At the beginning of the study, many people have a problem - the probabilistic meaning of the wave function and related things: the measurement process and the hypothesis of reduction of the wave function are difficult to understand. Moreover, in the future, when solving problems, this probabilistic meaning or interpretation, as a rule, is not required, therefore, many do not even think about it. Nevertheless, I would like to understand where it came from and why it is needed at all, and whether it is necessary at all. It turns out that the considerations, which probably formed the basis of such complex and contradictory postulates, became null and void as quantum electrodynamics progressed. Deep knowledge for understanding is not required - you can simply believe the well-known results from textbooks, but the initial level is still necessary.

On the problem of interpreting the wave function, disputes were conducted from the very beginning of the development of quantum mechanics. The most famous is the discussion between Bohr and Einstein, which lasted for many years. The interpretation of the wave function as the probability amplitude was developed mainly by Born [1] and supplemented by Bohr and Heisenberg [2] - physicists of the “Copenhagen School”. Later in the literature the name “Copenhagen interpretation” was adopted, hereinafter CI. I use the standard notation adopted in the Course of Theoretical Physics by L.D. Landau and E.M. Lifshitz [3] and in most other similar textbooks. The second part of the article proposes critical experiments that could refute or confirm CI. Unfortunately, they are not technically feasible in our time.

Probabilistic interpretation

In KI it is postulated that the wave function 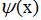is the amplitude of the probability density of the particle coordinates. It means thatis the probability density distribution of its detection at the point x. In this case, the concept of measurement and the postulate of reduction of the wave function, which does not follow from the Schrödinger equation, are introduced. If in all previous sections of physics the measurement process was concrete, described by the same equations and obeyed the same laws as any other physical process, then in quantum mechanics it is not defined clearly and is not described by clear equations. For example, in the classic textbook Landau and Lifshitz [3] absolutely incomprehensible words are sentenced that quantum mechanics needs a classical (non-quantum) device, etc. The most interesting thing is that in the future no classic device is required. It is completely incomprehensible during further study why the evolution of the wave function of an electron in interaction with a completely classical (with great accuracy, if we distract from the spin) by the object - the atomic nucleus, it is calculated using the Schrödinger equation and is well studied, and the interaction with the measuring device causes a mysterious reduction of the wave function, which cannot be proved using the Schrödinger equation. The reduction of the wave function is another postulate of CI that causes quite a few objections.

At present, the classical Born interpretation has undergone a fair revision, so many are not satisfied with either the concept of measurement or the mysterious reduction. Quite a lot of work on this topic has appeared. However, following the Born or some other interpretation does not affect the methods of solving problems in theory and the mathematical results obtained. Therefore, these works are more like philosophical or popularizing ones; it is difficult to attribute them to serious theoretical physics. For example, the multivariate interpretation proposed in 1957 by Everett [4], discussed in [5], introduces many variants of realities from which it is not known how the choice is made. New categories are introduced that are not used anywhere else. Such a number of different versions suggests that none is well-founded. At the same time, it is precisely an incomprehensible interpretation that greatly complicates the study of quantum mechanics at the initial stage. There is an axiomatic presentation of quantum theory [6], where there is no physical interpretation of the state vector at all. This is convenient for a mathematician, but a physicist is not suitable for a beginner.

All available works do not answer the simple question: “What made many first-class talents come to such a controversial interpretation in the 1920s and introduce concepts that were not defined even at the physical level of rigor - measurement, a classical device, and the hypothesis of wave function reduction, not backed by weighty arguments. " To understand, we must remember that in these years in quantum mechanics there was only one type of interaction - the electromagnetic field, and the main type of objects - electrons.

In classical field theory there are also auxiliary concepts - a test charge or a frame with current. But they are needed to explain the physical meaning of the introduced field strengths and potentials. A consistent and logical theory is constructed without them, on the basis of the Lagrangian of the field and charges. Since quantum mechanics is started, having already mastered field theory, the beginner has a question - is this probabilistic interpretation necessary at all? What is the bad point of view of Einstein, who considered particles simply as states of fields? Let's forget about the classical particles and just look at the field 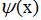for which there is the Schrödinger equation. Moreover, many authorities disagreed with the probabilistic interpretation (CI), both in the past (Einstein, de Broglie) and now (for example, Hawking). Just like the vector potential in electrodynamics,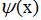does not have a direct physical meaning. Some quadratic expressions have physical meaning. For an electron, the charge density is - e , and the current density is e, m is the charge and mass of the electron, is Planck's constant. The experiments with electron diffraction on crystals and two slits are interpreted in this case very simply - the electron, like the light wave, passes immediately through the BOTH slots. From the Schrödinger equation, as well as from the wave equation for light, it is determined 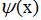on a photographic plate. Further, we assume that the degree of blackening is proportional by analogy with light, where the degree of blackening is proportional to the average ( E- electric field strength). This assumption is quite plausible. In this case, the Heisenberg uncertainty principle is just a well-known mathematical relation between the mean-square dispersion of a function and its Fourier image.

What arguments did the Copenhagen school have in favor of CI?

CI also allows you to interpret a number of experiments, for example, on electron diffraction. But the experiments are purely qualitative — blackening of the photographic plate was considered [7] . In principle, we can consider the simplest detector model consisting of a (x) -shaped hole in a large box. The electron gives off energy to the photon and passes to the bound level in the well. For the experiment to be correct, the localization radius in-the well should be much smaller than the electron wavelength. However, such a detector, as is easy to show, noticeably changes the stationary wave function of the electron in the box, so the experiment loses its meaning.

One of the main arguments of Bourne was that, according to the Schrödinger equation, the wave packet of a microscopic particle is indefinitely blurred with time. It seemed absurd to him. However, in the Bose - Einstein condensate, each particle is smeared over the entire macroscopic sample, so the Born argument is incorrect. There must be other arguments against the simplest field interpretation 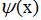close to Einstein's point of view.

Indeed, you can simply enter the complex fieldby postulating the expressions written above for the charge density and current, based on the continuity equation. The Schrödinger equation is derived in the usual way, and the Hamiltonian operator is a generalization of the classical expression for a charged particle. But then there arises an unsolvable problem at the then level of theory. With this approach, in the Hamiltonian of the hydrogen atom, it would be necessary, in addition to the interaction with the electrostatic field of the nucleus, to include the interaction of the electron cloud with its own electrostatic field, i.e. a term of the form

(1) would appear in energy

This term can also be derived as the energy of the electromagnetic field of the electron cloud, neglecting currents. For a hydrogen atom, such a term is of the same order as the interaction with the nucleus, i.e., a well-known and experimentally verified spectrum would change dramatically. Moreover, even for a free electron absurd consequences arise - Coulomb repulsion leads to the expansion of the wave packet and smearing of the electron cloud throughout the available space. Nothing of the kind is observed in the experiment. Perhaps this is precisely what led the Copenhagen school to CI, since all the above simple considerations probably came to their minds. Indeed, for a point particle such a term is absent; more precisely, it reduces to a constant. Further, for a helium atom, taking into account the Coulomb interaction of two electrons with each other gives quite plausible results, which again corresponds to the concept of point particles. That is, KI appeared for want of a better one. But in nonrelativistic quantum mechanics, particles do not arise and do not disappear. Then the assertion that the electron is at one point contradicts experiments with the diffraction of one electron on 2 slits. Also in the mentioned[7] experiment observed interference on a single electron crystal. So it’s simple and logical to explain the Schrödinger equation and well-known experiments on the basis of CI and known experiments. As a result, a certain algorithm was invented, which in some cases prescribes to consider an electron to be a particle, and in others - to be a wave, and called KI with the addition of “particle-wave dualism”. At the same time, the usual field interpretation seems impossible due to the absence of terms of type (1) in the energy, i.e. "Self-action" of one electron.

In fact, when writing (1), one unproven assumption was implicitly made - the electrons interact with the classical electromagnetic field. Can the electromagnetic field of an electron be considered classical? To understand, you need to use quantum electrodynamics. After all, in fact, there is no Coulomb potential, but there is an electromagnetic field interacting with electrons. In this case, the electromagnetic field included in the Schrödinger or Dirac equation for a hydrogen atom is fundamentally different from that which causes the interaction between electrons. It is classical, that is, it has a certain meaning at each point, and is generated by the classical object - the core.

In order to correctly investigate the problem, one needs to go over to relativistic quantum theory, then the wave function becomes an operator. There is no need (and also a place) to write the corresponding formulas and calculations, those who wish will find them in the textbook (see, for example, [8]). I confine myself to presenting the known results. Let's start with a free electron. To understand what will happen to his wave packet (or cloud), you need to find out how his Green's function or propagator changes due to interaction with an electromagnetic field. The corrections to the Green's function of a free electron, arising when the interaction with an electromagnetic field is taken into account, formally written according to perturbation theory, is known to be reduced to divergent integrals. However, this problem has been resolved. Was shown, that taking into account the interaction with a quantized electromagnetic field for a free electron simply leads to the replacement in the corresponding formulas of the charge and mass by the renormalized (observed) quantities [8]. Thus, in the nonrelativistic case of small momenta, taking into account the interaction of one electron with an electromagnetic field simply leads to the usual linear Schrödinger equation with renormalized charge and mass instead of term (1), that is, the assumption that the electromagnetic field is classical gives a fundamentally incorrect result in this case. A similar solution with renormalization exists for an electron in an external field — it is considered in the Lamb shift theory for a hydrogen atom [8, 9]. in the nonrelativistic case of small pulses, taking into account the interaction of one electron with an electromagnetic field simply leads to the usual linear Schrödinger equation with renormalized charge and mass instead of term (1), that is, the assumption that the electromagnetic field is classical gives a fundamentally incorrect result in this case. A similar solution with renormalization exists for an electron in an external field — it is considered in the Lamb shift theory for a hydrogen atom [8, 9]. in the nonrelativistic case of small pulses, taking into account the interaction of one electron with an electromagnetic field simply leads to the usual linear Schrödinger equation with renormalized charge and mass instead of term (1), that is, the assumption that the electromagnetic field is classical gives a fundamentally incorrect result in this case. A similar solution with renormalization exists for an electron in an external field — it is considered in the Lamb shift theory for a hydrogen atom [8, 9].

We now consider two electrons. For the case of small, nonrelativistic momenta, one can introduce some effective interaction between them into the Schrödinger equation. You can determine its form by the amplitude of the mutual scattering - it is uniquely associated with the interaction. In the Feynman diagram technique, diagrams with 4 external electronic lines correspond to it. In the case of small momenta, the corresponding scattering amplitude transforms into the Rutherford classical formula with allowance for exchange [8], that is, the interaction between the electrons in the atom can indeed be considered using the Coulomb potential.

Thus, unpleasant contradictions arising from the interpretation of the wave function as an ordinary field, without any corpuscular properties, can be eliminated if relativistic quantum theory is involved. However, insofar as the electromagnetic field is considered, this is quite logical. In any case, this is much more understandable than the notorious dualism and CI, and is close to Einstein's point of view. In relativistic theory, 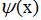it becomes already a quantized field, that is, for a given x, it is no longer a number, but an operator. But all these results were obtained approximately 30 years after the theoretical calculation of the spectrum of the hydrogen atom in the framework of nonrelativistic quantum mechanics and a remarkable coincidence with experiment. Over the years, CI has taken root in heads and textbooks.

The question may arise: why did the CI not disappear from the textbooks, if it is so easy to do without it now? I showed this article to several familiar professors from different universities and found that this subject was of little interest to them. For people who have already deeply mastered theoretical physics, it is irrelevant. It is also irrelevant for mathematicians working in theoretical physics. Large scientists generally ceased to be interested in learning and disseminating knowledge to the extent that it was 50 years ago. Landau was the last of the great theoretical physicists who put teaching and work with students on a par or higher than personal results, but he did not manage to master new methods of quantum electrodynamics - he had a fatal accident.

The measurement process, the values ​​of the physical quantity and stationary states. Other problems in understanding

From the probabilistic interpretation (CI) and the measurement process, which is not specified in any way, there is another confusion with the probabilities of states and the values ​​of some physical quantity F of a quantum particle. It is argued that the expansion coefficients 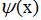in eigenfunctions are the probability amplitudes for detecting the corresponding eigenvalue or, which is the same, the probability amplitudes for the particle to be in the corresponding eigenstate. Once defined as a function giving a complete description of the properties of a particle or system, such a postulate is hardly perceived. Approximately, as the statement that in a bottle of vodka with a probability of 0.4 is pure alcohol, and with a probability of 0.6 - pure water. Further, it is postulated that the quantity is the average value of F in the probabilistic sense,- the operator corresponding to F. From here the student makes the completely incorrect conclusion that the value F can take only values ​​from its spectrum, and conservation laws are probabilistic in nature. This is completely wrong both from a formal point of view and from a physical one. The laws of conservation of the basic physical quantities - energy, momentum, angular momentum, etc., are much more fundamental than the Schrödinger equation, since they follow from the general properties of space-time. From a formal point of view, the quantity is conserved (independent of time) if the operator commutes with the Hamiltonian, i.e. if F is the integral of motion. In this case, it is logical to consider the value of F in the stateotherwise, it will be necessary to assume that, for example, energy is conserved only on average. Then the value of the physical quantity F (energy, momentum, angular momentum) of the particle can be any, that is, not necessarily an eigenvalue of the operator .

Considerable confusion in this area is created by considering exclusively stationary states, that is, the eigenvectors of the Hamiltonian. Students often have the conviction that there are no other states at all, and energy takes values ​​only from the spectrum of the Hamiltonian. Meanwhile, stationary states are idealization, in its pure form rarely existing. Much closer to reality (for example, for free particles) coherent states that minimize the uncertainty relation. The restriction of consideration exclusively to stationary states leads to the statement, wandering from textbook to textbook, that the energy of the electromagnetic field mode with frequency always changes by a multiple, i.e., an integer number of photons. But this is only true if the initial and final states are stationary, which is completely optional. In general, it is said almost universally in the educational literature that the electromagnetic field is a collection of photons, that is, non-stationary states are again ignored. This is completely incorrect, and leads to problems in solving simple problems. Consider, for example, an electron in a potential well with two levels . Somehow, for example, as a result of a short-term disturbance, he goes into the state and - wave functions corresponding to and . This state has more energy than the ground one, and over time the electron must return to the lower level, giving up excess energy to the electromagnetic field (we assume that the transitionnot forbidden due to some symmetries). It is easy to see that, if we restrict ourselves to the first order of the perturbation theory, then the transition can occur only as a result of interaction with the mode of the electromagnetic field of frequency . This follows from the time dependence of the initial and final wave functions in the Schrödinger representation. But the transition with the emission of a photon with energy is impossible due to the law of conservation of energy - the energy difference between the initial and final states is less . After this, the student concludes that the transition is prohibited. However, if we abandon the unfounded assumption that the final state is stationary, then the answer is easy. For definiteness, let the initial state of the electromagnetic mode c be ground, then its final statesatisfies the law of conservation of energy and has the desired frequency so that the transition of an electron to the ground level is possible. But talking about the birth of a photon is incorrect. From this example, by the way, it is seen that for a qualitative (simplified) explanation of the emission and absorption spectra in the nonrelativistic case, as well as the photoelectric effect, it is not necessary to use the "corpuscular" properties of electromagnetic waves.

The disassembled two-level problem is of greatest interest in relation to the electron spin. Let there be an electron in a bound state with spin along the x axis. We apply a magnetic field along the z axis. Then the wave function of the electron can be written in the form , where , a and- wave functions with spin along and against the z axis, which are eigenfunctions of the Hamiltonian. If you adhere to the CI, then with a probability of ½ an electron will emit a photon with energy . If we abandon the CI, as a result of emission we obtain the unsteady state of the electromagnetic field mode with frequency described above . Since it is always assumed that the frequency corresponds to energy , it is concluded from the total radiation energy that the number of emitted photons is half the number of electrons, i.e., half of the electrons were in the state. If during the experiment it was possible to distinguish an unsteady state with half energy from a standard photon, then it would be possible to give experimental confirmation or refutation of the CI. But, in any case, the Schrödinger equation, written for the electron and the photon mode , cannot lead to the emission of a photon with energy - this follows from the law of conservation of magnitude , where the operator is the Hamiltonian. This requires a mysterious reduction of the wave function.

One could distinguish a non-stationary state from a stationary one by the electron recoil momentum. In the second case (if KI is discarded), it is 2 times smaller. For a localized state of an electron with a binding energy E of the order of 10 ^-1the electron-volt ionization probability will be different in both cases, and the ionization threshold in the magnetic field will be 2 times different. Unfortunately, the estimate shows that too strong magnetic fields of 10 ¹¹ gs are needed for ionization . Such fields are currently unattainable.

It would be possible to use free electrons for experimental verification, the spin orientation of which is given by a magnetic field. Let us consider a setup consisting of a chamber with free electrons in a strong magnetic field along the z axis. Electrons fly out of the hole in the chamber with a magnetic field, having a spin along the z axis, into the chamber, where 2 identical disks with holes displaced by an angle φ are located on the rotating axis. Such a setup makes it possible to obtain an electron beam of the same energy parallel to the x axis. Once in a magnetic field directed along the x axis, electrons with spins oriented along the z axis should start emitting frequency photonsor the above non-stationary modes of the same frequency. In this case, the recoil momentum can reduce or increase the speed of the electron. If the speed of the electrons in the beam is sufficiently small, then electrons will appear, flying backward, which can be detected. This would allow a critical experimental verification of CI. Unfortunately, at the highest magnetic fields currently achievable ~ 10 ⁶ G, the recoil momentum corresponds to an energy of 3 * 10 ^-11 eV or a velocity of the order of 3 m / s. It is difficult enough to provide such a low electron velocity, since it is much less than the thermal.

Conclusion

Field interpretation allows returning quantum mechanics to the framework of a systematic exposition adopted in the remaining sections of the course of theoretical physics. Indeed, all volumes of the theoretical physics course by Landau and Lifshitz are constructed according to a single scheme, with a clear system of concepts and postulates, and only volume 3 is based on some external concepts like the measurement process, a classical device, etc., and these concepts themselves are clearly not defined.

It is therefore not surprising that there is evidence of the niece of L.D. Landau [10] that he himself, having placed in his famous “Course in Theoretical Physics” a detailed exposition of CI [3], treated her completely indifferently:
“To my brother, then a student, Lena Kardashinsky, according to his literal recollections, in answer to the question: what is an electron, Dau, in his decisive manner characteristic of him, answered:“ The electron is not a corpuscle and not a wave. From my point of view - he is an equation, in the sense that his properties are best described by the equation of quantum mechanics, and there is no need to resort to other models - corpuscular or wave ”. ". The conclusions of this article are, in general, in line with Landau's opinion - no additional concepts, postulates, etc. are needed. to explain the physical meaning of quantum mechanics. The traditional notion of a field is enough.

As I wrote above, for specialists this issue is usually irrelevant. But for physics students who master the material and try to understand the physical meaning of the formulas, it is very important. Especially now, when the general interest in physics fell below the plinth.

If the article arouses interest, I can write a sequel on the so-called "quantum entanglement." In fact, this name in Russian-language materials comes from illiteracy - in textbooks, for example, [3] §14, these conditions are always called mixed, but the authors of the articles, it seems, have not read the textbooks. From simple reasoning, it will be clear why no quantum teleportation of information exists, and why spectacular experiments with these states are of little interest to science. These are effects on the public, and not for specialists.

Literature:

1. Born M. Statistical interpretation of wave mechanics // Atomic Physics - M .: Mir, 1965
2. Heisenberg V. Development of the interpretation of quantum theory // Niels Bohr and the development of physics / collection of books. edited by Pauli V. - M: IL, 1958. - P. 23-45.
3. Landau, L. D., Lifshits, E. M. Quantum mechanics (nonrelativistic theory). - 3rd edition, revised and supplemented. - M .: Nauka, 1974.- 752 p. - (“Theoretical Physics”, Volume III).
4. Hugh Everett. “Relative State” Formulation of Quantum Mechanics. Rev. Mod. Phys., Vol. 29, N 3, July 1957.
5. Mensky M. B. Man and the quantum world. Fryazino: Vek2, 2005. - 320 p. - (Science for everyone). ISBN 5-85099-161-1 UDC 530.1 BBK 22.31 M50
6. Bogolyubov N. N., Logunov A. A., Todorov I.T. Fundamentals of the axiomatic approach in quantum field theory., “Science”, Main Edition of the Physics and Mathematics Literature, 1969 E30.1 B 74 UDC B30.14B
7. Diffraction of single alternately flying electrons. From the current literature. Physics-Uspekhi, 1949 August, XXXVIII, no. 4
ufn.ru/ufn49/ufn49_8/Russian/r498e.pdf
8. Akhiezer A. I., Berestetskiy V. B. Quantum electrodynamics. - 3rd edition, revised. - M .: Nauka, 1969 .-- 623 p.
9. P.A.M. Dirac. Lectures on quantum field theory. Translated from English by B. A. Lysov. Edited by A. A. Sokolov. Mir Publishing House, Moscow 1971
10. Ella RYDINA. Leo Landau: strokes for the portrait // Bulletin, No. 5, 6, 7 (No. 342-344). March 2004 www.vestnik.com/issues/2004/0303/win/ryndina.htm