What holds the nuclei of atoms?
- Transfer
Now that we know that the nucleus of an atom is tiny , we have an obvious question: why is it so small? Atoms are made up of tiny particles, but they are much larger in size . We have already figured out why this is happening. But at the same time, the nuclei do not differ greatly in size from the protons and neutrons of which they consist. Is there a reason for this, or is it a coincidence?
We already know that atoms hold electrical forces . What forces hold the nucleus of an atom?
And here we are entering a new territory, very different from what we studied earlier - because it becomes obvious that a force is working here that we have not yet discussed.
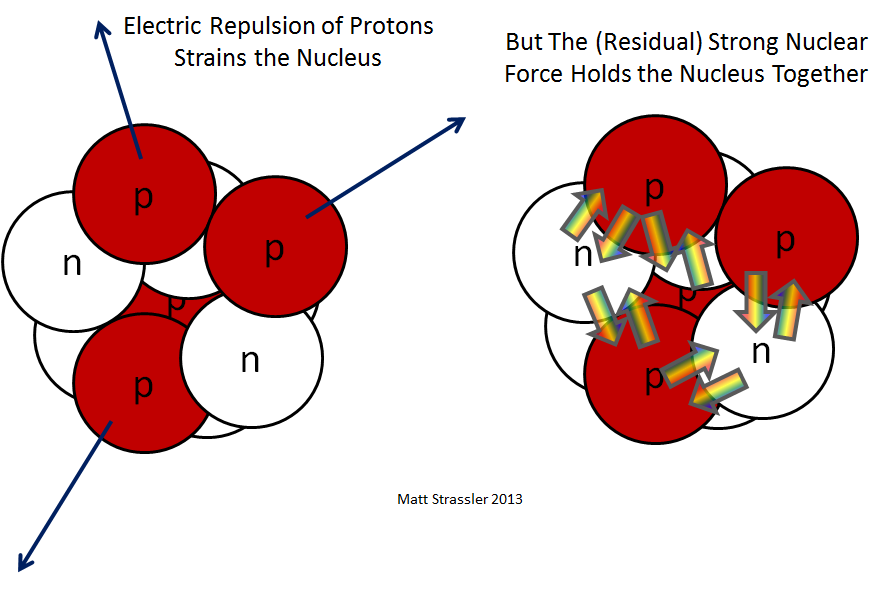
Fig. 1: the opposing forces in the nucleus of an atom - the electrical repulsion of protons and the residual strong nuclear interaction of protons and neutrons
If only gravitational and electrical interactions existed in nature, which we encounter in everyday life, nuclei with many protons would simply fly apart: the electric forces pushing protons apart from each other would exceed their gravitational attraction by a million million million times. So there must be another force that provides attraction, overpowers electric repulsion. This force is a strong nuclear interaction - although only the shadow of its true greatness can be observed in the core itself. Having studied the structure of the protons and neutrons themselves, we will understand the true possibilities of strong nuclear interaction. And in the core we find only what is often called “residual interaction” - and I will call it “residual strong nuclear interaction”.
Warning: in the end, it turns out that although in general strong nuclear interaction - the force acting between particles (quarks, gluons, antiquarks) inside a proton or neutron - is quite simple, in a sense, the residual strong nuclear interaction is a complex residue of various mutually annihilating effects, in connection with which there is no simple picture describing the entire physics of the nucleus. And this is not surprising, given the internal complexity of the structure of protons and neutrons. Here we can draw a certain analogy between atoms and molecules.
In an atom, a tiny nucleus and even smaller electrons are located far from each other in relation to their size, and the electric forces that hold them in the atom are simple. But in molecules, the distance between atoms is comparable to the size of atoms, so the internal complexity of atoms begins to play a role. The variety and complex sets of partially compensating electric forces, and the processes in which electrons are able to move between atoms, make the history of molecules much richer and more complicated than that of atoms. Also, the distance between protons and neutrons in the nucleus is comparable to their size - therefore, like with molecules, the forces that hold atomic nuclei turn out to be much more complicated (in certain senses) of the forces that hold protons or neutrons.
After studying the structure of protons and neutrons, this story will become (a little) cleared up. The basic properties of nuclear physics are quite clear, but this topic remains extremely technical, and many details are still being investigated. I will not be able to properly describe it in this article, in particular because I am not well versed in this topic in order to conveniently simplify it for you.

Fig. 2: The lightest of stable and nearly stable nuclei, together with a neutron. The neutron and tritium are indicated by a dotted line, as they eventually decay. Alternate names are indicated in blue.
Let's see what can be learned from simple reasoning about the work of this force. One clue is that all nuclei, with the exception of the most common hydrogen isotope (one proton), contain neutrons; that is, there are no nuclei with several protons and without neutrons (Fig. 2). So clearly neutrons play an important role in helping protons stick together.
Conversely, there are no nuclei consisting of neutrons alone; in the lightest nuclei, for example, in oxygen or silicon, there are approximately as many neutrons as protons (Fig. 2). In larger and more massive nuclei, for example, gold and radium, there are slightly more neutrons than protons (Fig. 3). Two things follow from this:
An illustration of the last statement is presented in Fig. 3, which shows stable (black) and relatively long-lived, but unstable (colored) nuclei, in the form of a graph of the dependence of the number of protons Z on the number of neutrons N contained in them. Note that for stable nuclei, Z and N are approximately equal at small values, but N gradually becomes larger than Z, with their increase. Also note that the band of stable and long-lived nuclei remains quite narrow for all Z values. Despite the tremendous progress of nuclear physics over the past 80 years, there is no universally accepted and simple explanation for this remarkable fact. I think he is considered a strange coincidence.
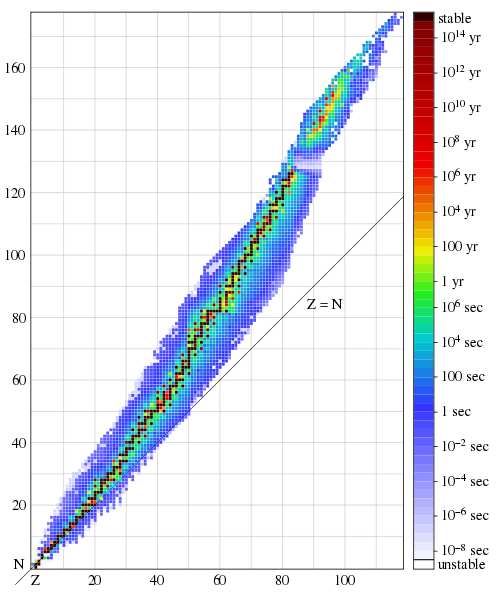
Fig. 3
One of the main goals of this article is to explain why the nuclei of atoms are small compared to the size of an atom. To do this, we start with the simplest nucleus containing protons and neutrons - with the second most common isotope of hydrogen, consisting of one electron (like all hydrogen isotopes) and a nucleus consisting of a proton and neutron. This isotope is often called deuterium, and the deuterium nucleus (see Fig. 2) is sometimes called the deuteron. How to understand what holds the deuteron? We can naively assume that this system does not differ from the hydrogen atom, which also contains two particles (proton and electron) - see Fig. 4.
As we saw in the previous article , the fact that the mass of electrons is small compared with protons and neutrons ensures that:
What about a deuteron? It similarly consists of two objects, but of almost equal mass (the mass of the neutron and proton differs by only 1/1500, for reasons that we will understand later), so both of them are equally important in determining the mass and size of the deuteron. Suppose we would have a new force that attracts a proton to a neutron, similar to an electromagnetic one (in fact, everything is wrong, but just imagine): then, by analogy with hydrogen, we would expect that the size of the deuteron would be inversely proportional to the mass of the proton or neutron, and is inversely proportional to the strength of the new interaction. If this interaction were as strong at a certain distance as electromagnetism, it would mean that, since the proton is about 1850 times heavier than the electron, the deuteron (and any nucleus) should be at least 1000 times less than hydrogen.
But we already guessed that the residual strong interaction is stronger than electromagnetism at the same distance - because otherwise it could not have prevented the electromagnetic repulsion of protons that would break the nucleus. So this additional force will pull together protons and neutrons together even denser. Therefore, it is not surprising that the deuteron and other nuclei are not just a thousand, but tens of thousands of times smaller than atoms! I repeat, this is all because:
This naive conjecture led us to an almost correct answer! But it does not fully describe the complexity of the interactions between a proton and a neutron in deuterium. One obvious problem is a force similar to electromagnetism, but a large one in power would obviously affect everyday life, and we do not observe anything like this. So something at this interaction should differ from electric.
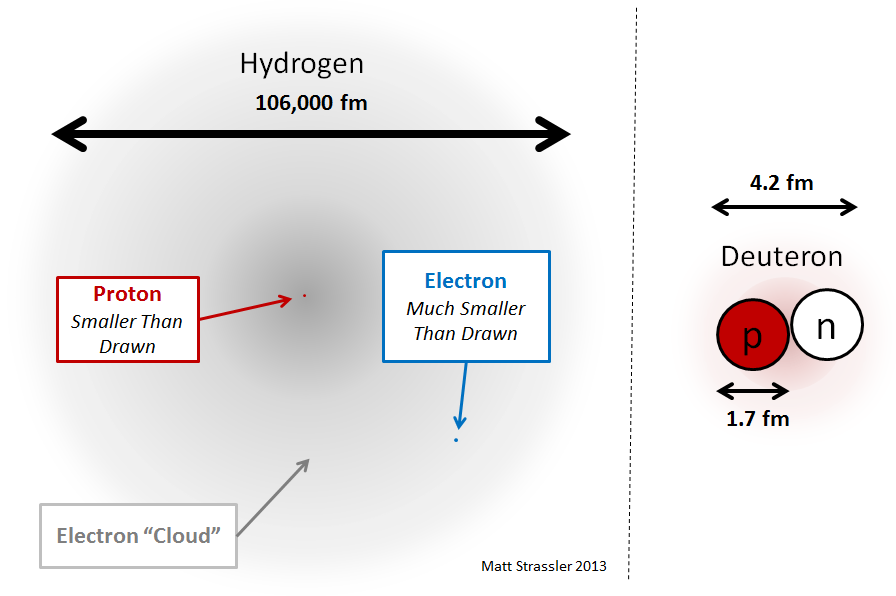
Fig. 4
The difference is that this residual strong nuclear interaction is very important and powerful for protons and neutrons located very close to each other, but at sufficiently large distances (at a distance of the force) it begins to decrease very quickly, much faster than electromagnetic. The distance - by some coincidence - turns out to be equal to the size of a relatively large nucleus, only several times larger than the proton. If you bring the proton and neutron together, at a distance comparable to this distance, they will be attracted to each other and form a deuteron. If you leave them at a greater distance, they almost do not feel the attraction. And if you bring them very close together, so that they overlap each other, they will begin to push off; hell, I warned you that the residual strong nuclear interaction is very complex! In short:
Larger nuclei are held more or less by the same interaction that holds the deuteron, but the details of this process are complex and technical, and they are not easy to describe. Yes, they are still not fully understood. Although the general contours of nuclear physics have been well understood for decades, many important details are still being explored.
We already know that atoms hold electrical forces . What forces hold the nucleus of an atom?
And here we are entering a new territory, very different from what we studied earlier - because it becomes obvious that a force is working here that we have not yet discussed.

Fig. 1: the opposing forces in the nucleus of an atom - the electrical repulsion of protons and the residual strong nuclear interaction of protons and neutrons
Residual strong nuclear interaction
If only gravitational and electrical interactions existed in nature, which we encounter in everyday life, nuclei with many protons would simply fly apart: the electric forces pushing protons apart from each other would exceed their gravitational attraction by a million million million times. So there must be another force that provides attraction, overpowers electric repulsion. This force is a strong nuclear interaction - although only the shadow of its true greatness can be observed in the core itself. Having studied the structure of the protons and neutrons themselves, we will understand the true possibilities of strong nuclear interaction. And in the core we find only what is often called “residual interaction” - and I will call it “residual strong nuclear interaction”.
Warning: in the end, it turns out that although in general strong nuclear interaction - the force acting between particles (quarks, gluons, antiquarks) inside a proton or neutron - is quite simple, in a sense, the residual strong nuclear interaction is a complex residue of various mutually annihilating effects, in connection with which there is no simple picture describing the entire physics of the nucleus. And this is not surprising, given the internal complexity of the structure of protons and neutrons. Here we can draw a certain analogy between atoms and molecules.
In an atom, a tiny nucleus and even smaller electrons are located far from each other in relation to their size, and the electric forces that hold them in the atom are simple. But in molecules, the distance between atoms is comparable to the size of atoms, so the internal complexity of atoms begins to play a role. The variety and complex sets of partially compensating electric forces, and the processes in which electrons are able to move between atoms, make the history of molecules much richer and more complicated than that of atoms. Also, the distance between protons and neutrons in the nucleus is comparable to their size - therefore, like with molecules, the forces that hold atomic nuclei turn out to be much more complicated (in certain senses) of the forces that hold protons or neutrons.
After studying the structure of protons and neutrons, this story will become (a little) cleared up. The basic properties of nuclear physics are quite clear, but this topic remains extremely technical, and many details are still being investigated. I will not be able to properly describe it in this article, in particular because I am not well versed in this topic in order to conveniently simplify it for you.

Fig. 2: The lightest of stable and nearly stable nuclei, together with a neutron. The neutron and tritium are indicated by a dotted line, as they eventually decay. Alternate names are indicated in blue.
Scheme of work
Let's see what can be learned from simple reasoning about the work of this force. One clue is that all nuclei, with the exception of the most common hydrogen isotope (one proton), contain neutrons; that is, there are no nuclei with several protons and without neutrons (Fig. 2). So clearly neutrons play an important role in helping protons stick together.
Conversely, there are no nuclei consisting of neutrons alone; in the lightest nuclei, for example, in oxygen or silicon, there are approximately as many neutrons as protons (Fig. 2). In larger and more massive nuclei, for example, gold and radium, there are slightly more neutrons than protons (Fig. 3). Two things follow from this:
- For protons to stick together, neutrons are needed, and for neutrons to stick together, protons are needed.
- If the number of protons and neutrons becomes very large, then the electrical repulsion of protons must be compensated by the addition of several additional neutrons.
An illustration of the last statement is presented in Fig. 3, which shows stable (black) and relatively long-lived, but unstable (colored) nuclei, in the form of a graph of the dependence of the number of protons Z on the number of neutrons N contained in them. Note that for stable nuclei, Z and N are approximately equal at small values, but N gradually becomes larger than Z, with their increase. Also note that the band of stable and long-lived nuclei remains quite narrow for all Z values. Despite the tremendous progress of nuclear physics over the past 80 years, there is no universally accepted and simple explanation for this remarkable fact. I think he is considered a strange coincidence.

Fig. 3
Core size
One of the main goals of this article is to explain why the nuclei of atoms are small compared to the size of an atom. To do this, we start with the simplest nucleus containing protons and neutrons - with the second most common isotope of hydrogen, consisting of one electron (like all hydrogen isotopes) and a nucleus consisting of a proton and neutron. This isotope is often called deuterium, and the deuterium nucleus (see Fig. 2) is sometimes called the deuteron. How to understand what holds the deuteron? We can naively assume that this system does not differ from the hydrogen atom, which also contains two particles (proton and electron) - see Fig. 4.
As we saw in the previous article , the fact that the mass of electrons is small compared with protons and neutrons ensures that:
- The mass of an atom is almost equal to the mass of its nucleus,
- The size of an atom (the size of an electron cloud) is inversely proportional to the mass of the electron and inversely proportional to the strength of the electromagnetic interaction; the uncertainty principle of quantum mechanics plays a critical role here.
What about a deuteron? It similarly consists of two objects, but of almost equal mass (the mass of the neutron and proton differs by only 1/1500, for reasons that we will understand later), so both of them are equally important in determining the mass and size of the deuteron. Suppose we would have a new force that attracts a proton to a neutron, similar to an electromagnetic one (in fact, everything is wrong, but just imagine): then, by analogy with hydrogen, we would expect that the size of the deuteron would be inversely proportional to the mass of the proton or neutron, and is inversely proportional to the strength of the new interaction. If this interaction were as strong at a certain distance as electromagnetism, it would mean that, since the proton is about 1850 times heavier than the electron, the deuteron (and any nucleus) should be at least 1000 times less than hydrogen.
But we already guessed that the residual strong interaction is stronger than electromagnetism at the same distance - because otherwise it could not have prevented the electromagnetic repulsion of protons that would break the nucleus. So this additional force will pull together protons and neutrons together even denser. Therefore, it is not surprising that the deuteron and other nuclei are not just a thousand, but tens of thousands of times smaller than atoms! I repeat, this is all because:
- Protons and neutrons are almost 2000 times heavier than electrons,
- At such distances, the strong nuclear interaction between the protons and neutrons of the nucleus is many times stronger than the corresponding electromagnetic forces (including the electromagnetic repulsion of protons in the nucleus).
This naive conjecture led us to an almost correct answer! But it does not fully describe the complexity of the interactions between a proton and a neutron in deuterium. One obvious problem is a force similar to electromagnetism, but a large one in power would obviously affect everyday life, and we do not observe anything like this. So something at this interaction should differ from electric.

Fig. 4
Short range of action of this force
The difference is that this residual strong nuclear interaction is very important and powerful for protons and neutrons located very close to each other, but at sufficiently large distances (at a distance of the force) it begins to decrease very quickly, much faster than electromagnetic. The distance - by some coincidence - turns out to be equal to the size of a relatively large nucleus, only several times larger than the proton. If you bring the proton and neutron together, at a distance comparable to this distance, they will be attracted to each other and form a deuteron. If you leave them at a greater distance, they almost do not feel the attraction. And if you bring them very close together, so that they overlap each other, they will begin to push off; hell, I warned you that the residual strong nuclear interaction is very complex! In short:
- The residual strong nuclear interaction is much, much weaker than electromagnetism at distances much larger than the size of a typical nucleus, so we do not meet it in everyday life.
- At short distances comparable to the nucleus, it becomes much stronger - this attraction (at not too short distances) can exceed the electrical repulsion of other protons.
Larger nuclei are held more or less by the same interaction that holds the deuteron, but the details of this process are complex and technical, and they are not easy to describe. Yes, they are still not fully understood. Although the general contours of nuclear physics have been well understood for decades, many important details are still being explored.
