Color: Hex to Eye
- Transfer
Why do we perceive
background-color: #9B51E0this particular purple color? 
For a long time, I thought I knew the answer to this question. But after a good reflection, he realized significant gaps in his knowledge.
Now I hope to fill some of these gaps by studying electromagnetic radiation, optical biology, colorimetry, and color imaging equipment. If you want, you can skip to a specific section, here is the table of contents:
- Electromagnetic radiation
- Visible light
- Perceptible brightness
- Color quantification
- Optical biology
- Color spaces
- Wright and Guild Color Experiments
- Visualization of color spaces and chromaticity
- Gamma and spectral locus
- CIE XYZ color space
- Screen subpixels
- sRGB
- Hexadecimal sRGB codes
- Gamma correction
- From hexadecimal codes to the eye
- Brief note on adjusting brightness
- Things I missed
- References
Otherwise, let's start with physics.
Electromagnetic radiation
Radio waves, microwaves, infrared radiation, visible light, ultraviolet light, x-rays and gamma radiation are all forms of electromagnetic radiation. Although they are called differently, these names simply refer to different wavelength ranges in the electromagnetic spectrum.
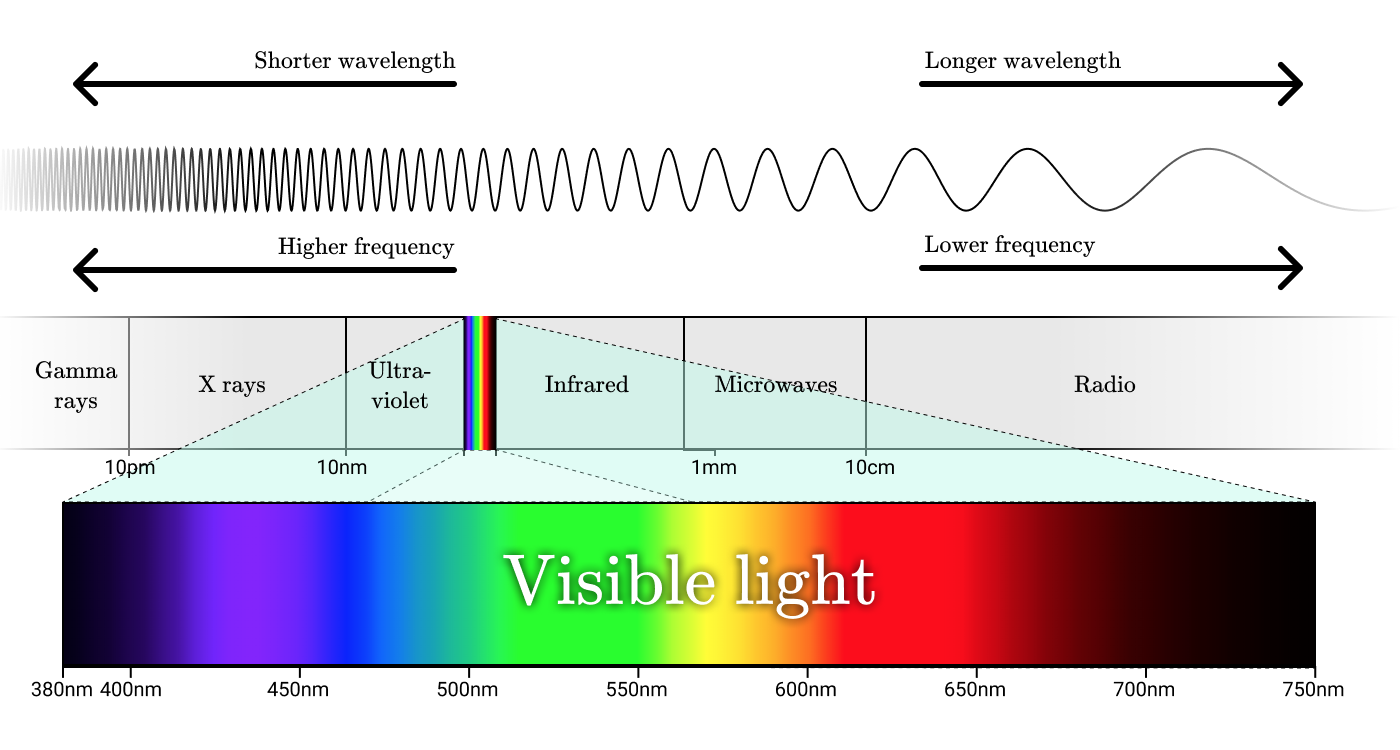
Electromagnetic spectrum
The smallest unit of electromagnetic radiation is a photon. The photon energy is proportional to the frequency of the corresponding wave, and high-energy photons correspond to high-frequency waves.
To understand color, one must first understand radiation. Let’s take a closer look at the light from an incandescent lamp.

Photo: Alex Iby
We can ask you how much energy the lamp emits. Radiation flux (
If we want to know how much energy falls on each wavelength range, then we can look at the spectral density of the radiation . Spectral radiation density (
If we depict the spectral radiation density of our incandescent bulb as a function of wavelength, it will look something like this:

The area of the region bounded by this curve corresponds to the radiation flux. In the form of an equation:
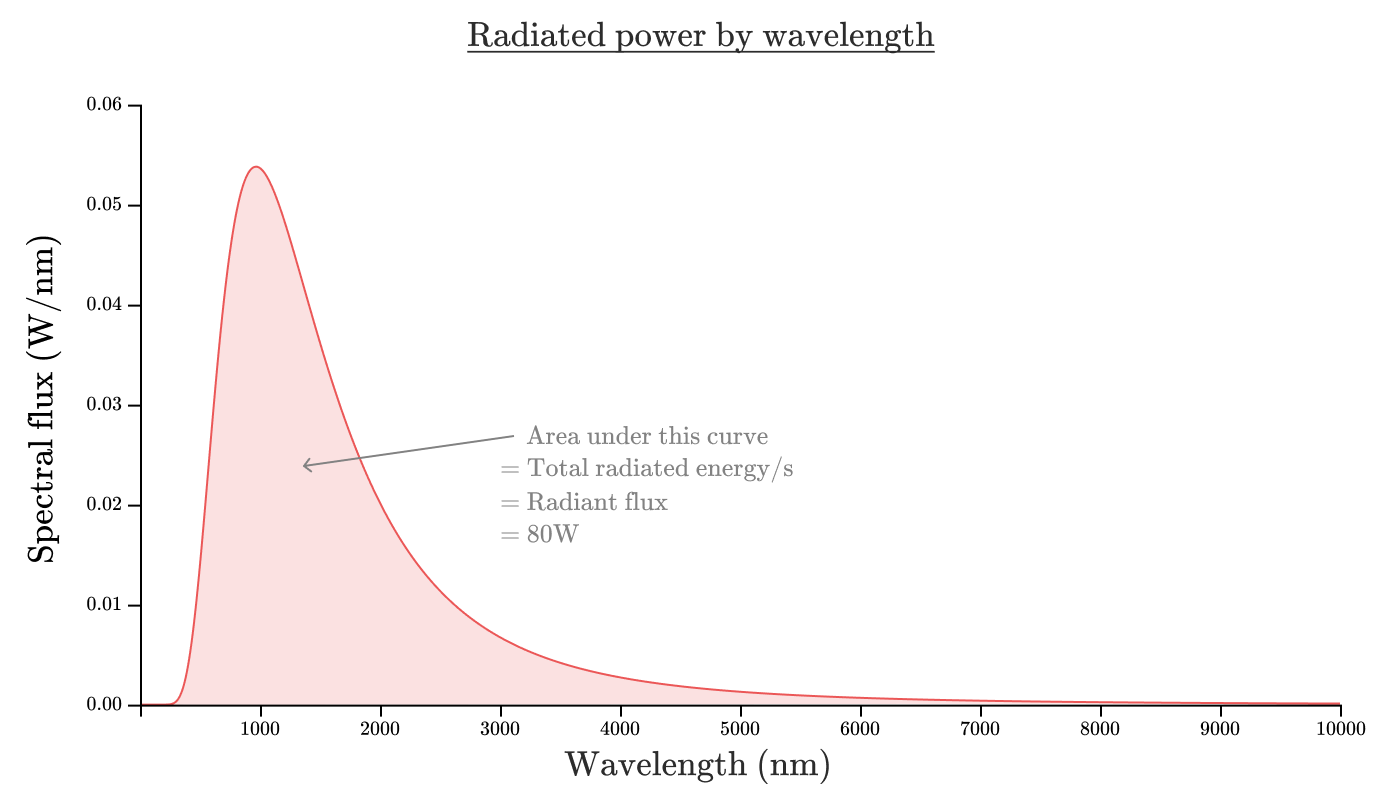
You may have heard from environmentalists that incandescent bulbs are extremely ineffective and you think: “Hmm, 80% doesn’t seem such a bad efficiency.”
And it is true. An incandescent bulb is a very effective way to convert electricity to radiation. Unfortunately, this is a terrible way to convert electricity into human visible radiation.
Visible light
Visible light is in the wavelength range from

So, in the visible range , 8.7 W is emitted, which gives us an efficiency of 8.7%. It looks awful. In fact, the situation is even worse.
To understand why, let's look at why visible light is visible .
Perceptible brightness

Photo: Christopher Burns
Just as an incandescent lamp does not emit equally at all wavelengths, our eyes are also not equally sensitive to radiation in all ranges. If we measure the sensitivity of the human eye to each wavelength, then we obtain a function of the relative spectral light efficiency of monochromatic radiation . Standard Spectral Luminous Efficiency Function
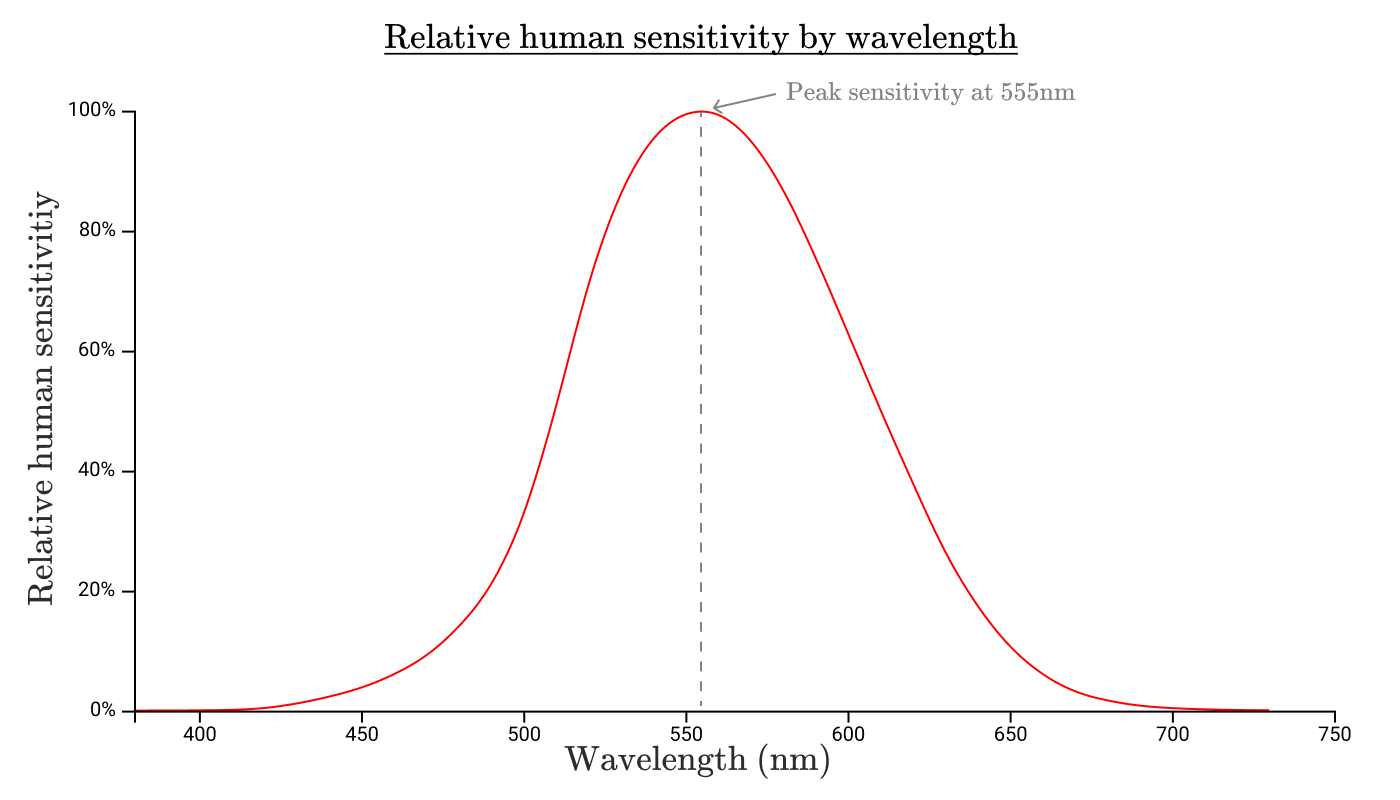
The boundaries of this function determine the range of visible light. We will not see anything outside this range, because our eyes do not perceive this light!
This curve also shows that our eyes are much more sensitive to radiation at 550 nm than to radiation at 650 nm or 450 nm.
The eyes of other animals are sensitive to other ranges of waves and, therefore, other functions of relative spectral light efficiency act for them. Birds can see radiation in the UV range from

Photo: Timothy Rhyne
Multiplying the plot of the spectral density of radiation by a function of the relative spectral light efficiency of monochromatic radiation
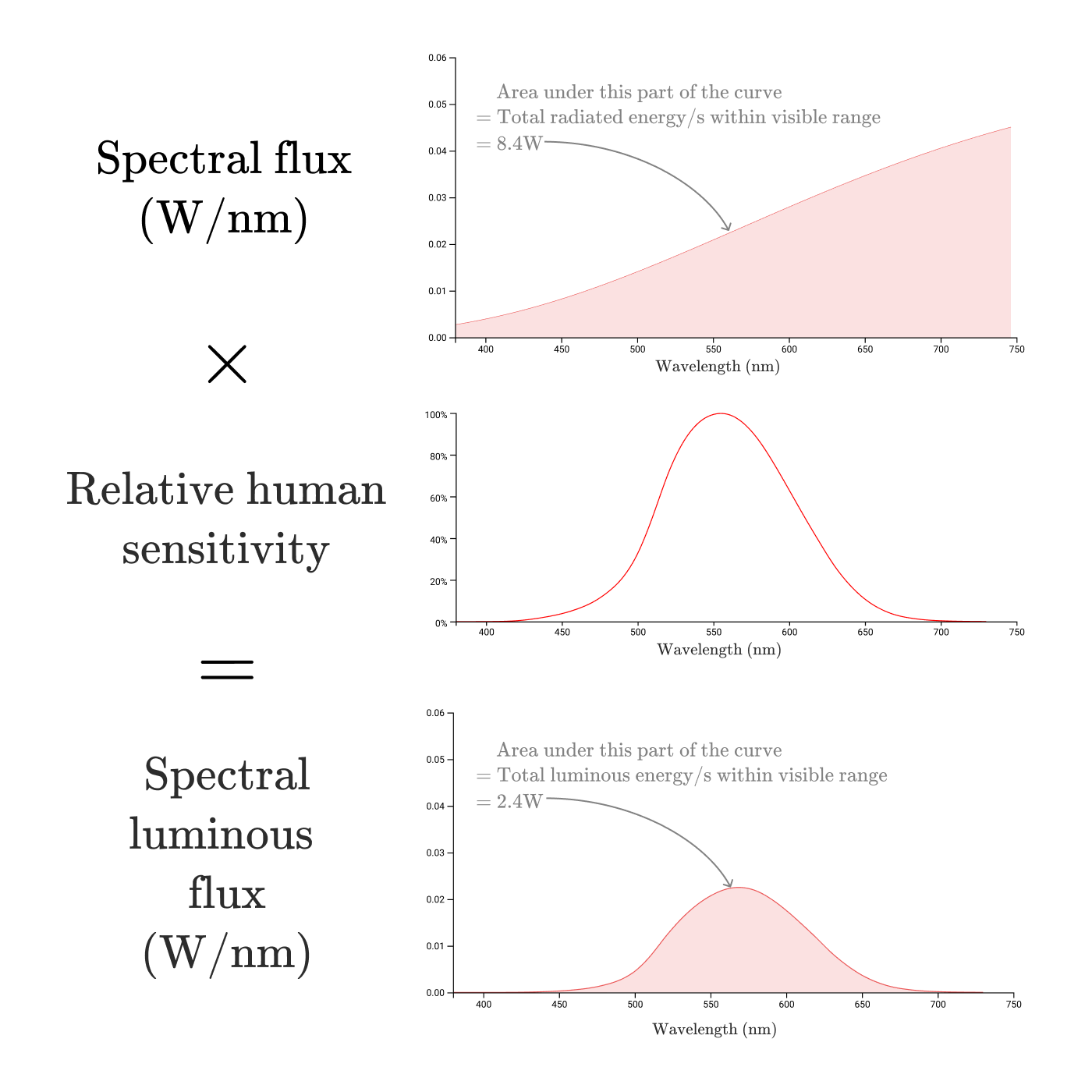
This is the spectral density of the light flux (
Luminous flux (
Just as we calculated the radiation flux by calculating the area of the region bounded by the curve of the radiation flux, we can find the luminous flux by taking the region bounded by the spectral density curve of the light flux , with the conversion from watts of perceived radiation to lumens:
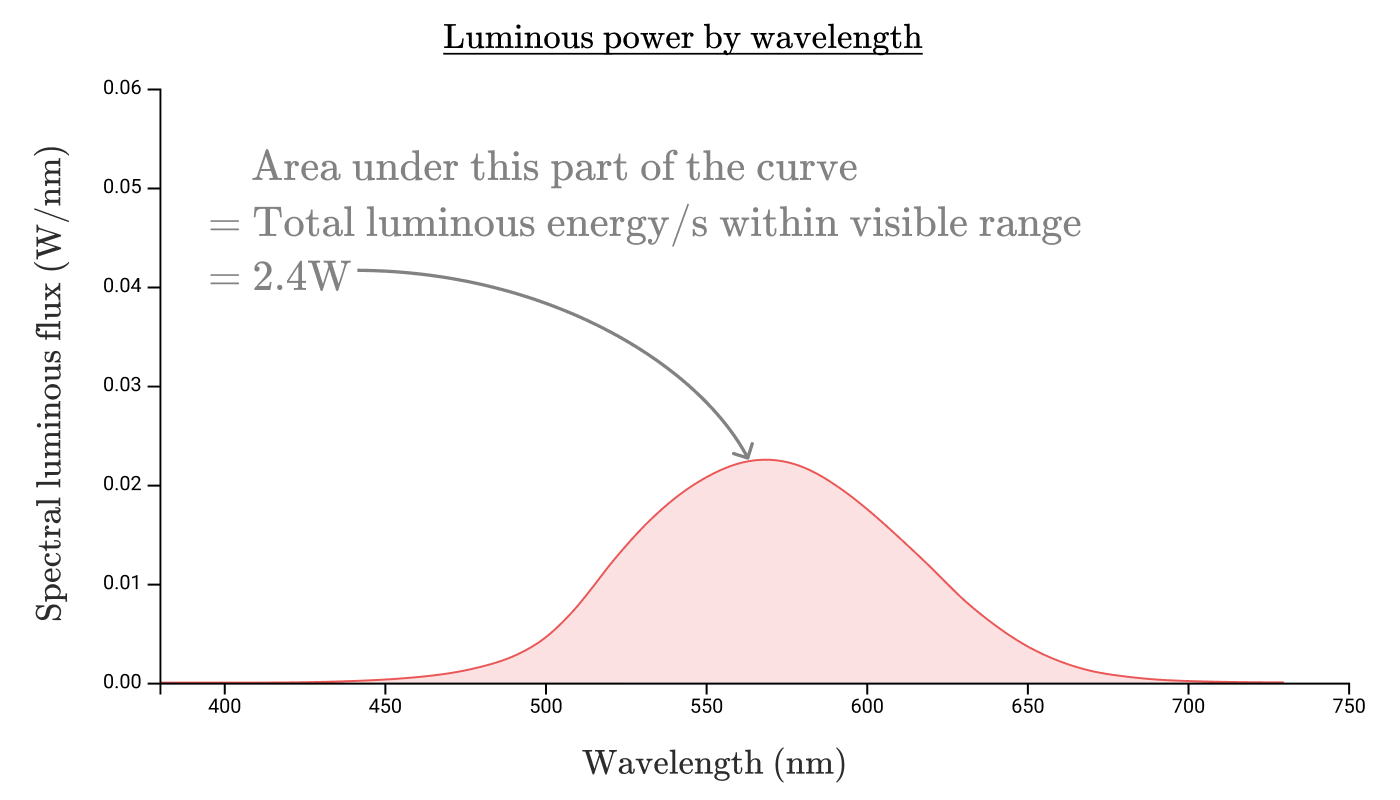
So the luminous flux of our 100-watt incandescent lamp is a miserable 2.4 W or 1600 lumens! An incandescent lamp has a luminous efficiency of only 2.4%, which is far from the efficiency of 80% conversion of electricity into radiation.
Perhaps if our light source concentrated its radiation in the visible range, then we could get more efficient lighting. Let us compare the spectra of incandescent, fluorescent and LED lamps:

Indeed, fluorescent and LED lamps spend much less energy in ranges invisible to humans. If incandescent lamps have an efficiency of 1-3%, then for fluorescent lamps it is about 10%, and for LED lamps it is up to 20%!
But enough about the brightness, back to the topic of the article: color!
Color quantification

Photo: Lauren Mancke
How to identify this color? If there is a lemon in front of me, how can I say on the phone what color it is? I can say that the lemon is yellow, but which one is yellow? How to accurately identify each of these shades of yellow?

Armed with the knowledge that color is a person’s interpretation of electromagnetic radiation, it may be tempting to determine color mathematically using the spectral density of radiation. Any color seen by a person will be a kind of balanced combination of monochromatic colors (single wavelengths). Monochromatic colors are also known as spectral colors.
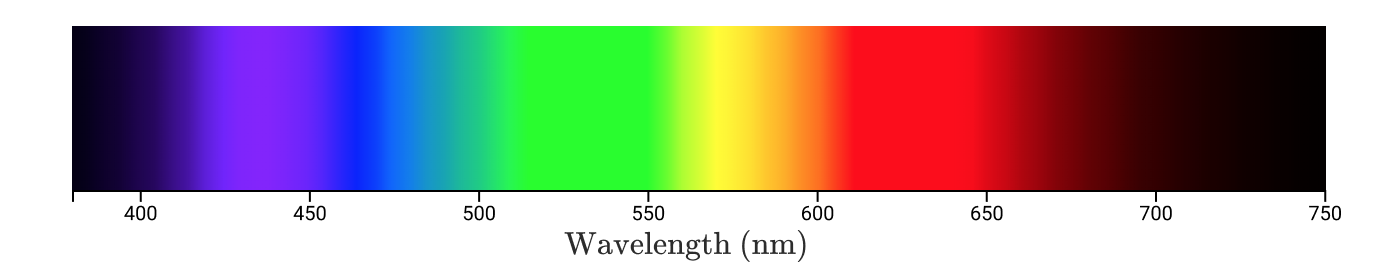
Monochromatic wavelength colors
For any given object, you can measure the spectrum of radiation (or reflection) - and use it to accurately determine the color. If you can reproduce the spectrum, then we will accurately reproduce the color!
The sunlight reflected from a point on a lemon may have approximately the following reflection spectrum:
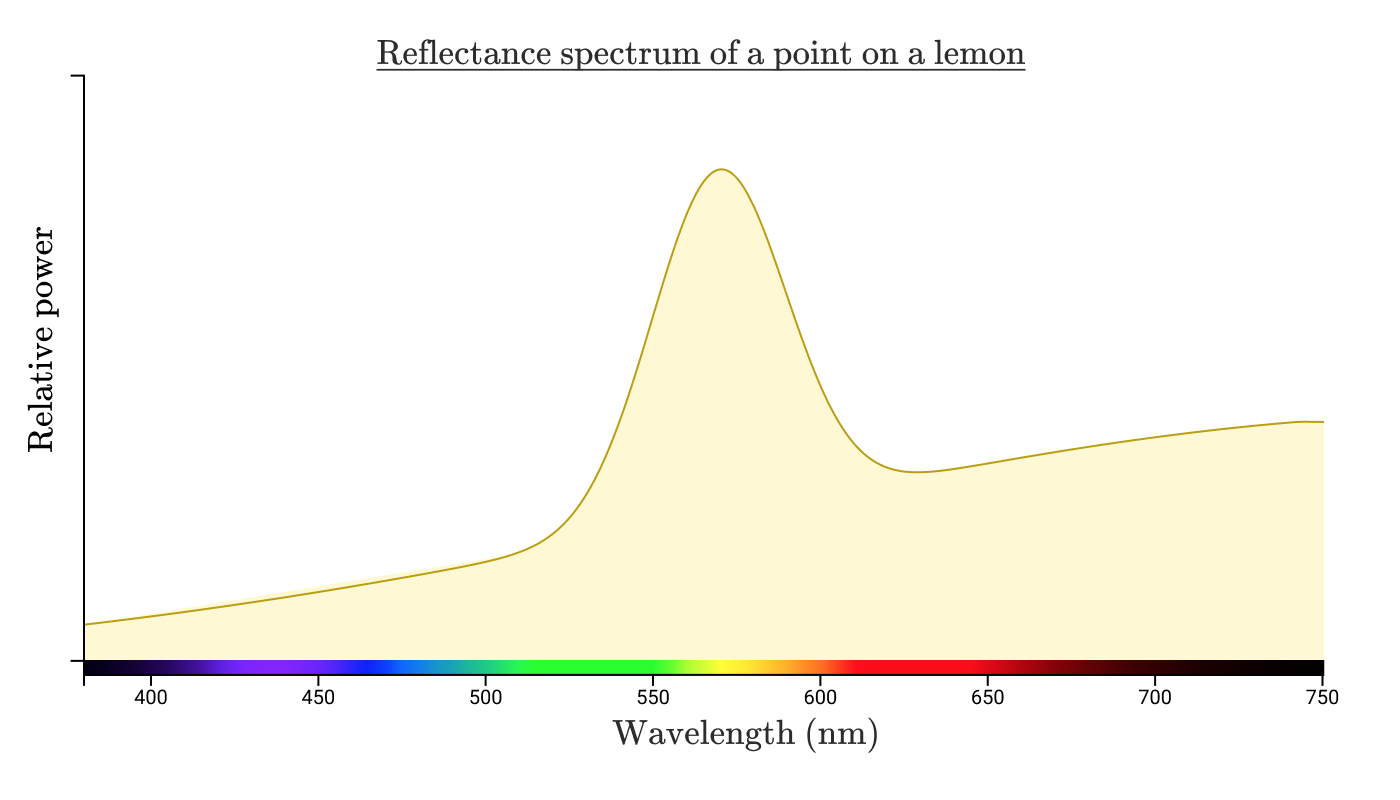
Note: the power and intensity distribution of the radiation reaching the eye depends on the power and emission spectrum of the light source, the distance from the light source to the illuminated object, the size and shape of the object, the absorption spectrum object and the distance from you to the object. There is a lot to think about, so let's focus on what happens when this light reaches the human eye. For now, ignore units and focus on concepts.
When energy with such a spectral distribution enters the human eye, he perceives it as "yellow." Suppose I took a picture of a lemon and uploaded the photo to a computer. Then he carefully adjusted the colors on the screen so that the specific point of the lemon on the screen does not differ from the color of the actual lemon in my real hand.
If you measure the spectral intensity distribution from the screen, how do you think it will look? It is reasonable to expect that it is similar to the reflection spectrum of the lemon above. But in reality it looks something like this:

Two different distributions of spectral intensity that look the same for a human observer are called metamers .
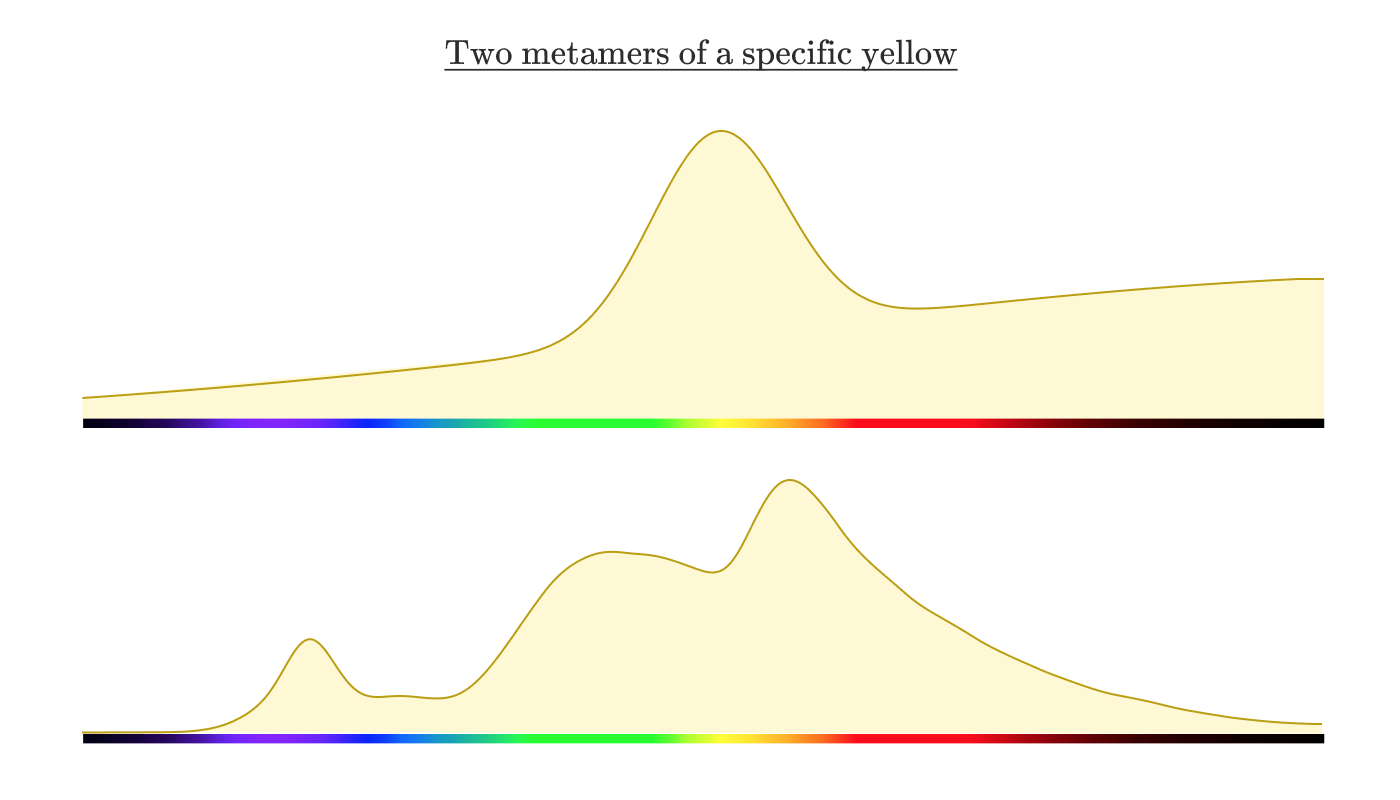
To understand how this is possible, consider the biology of the eye.
Optical biology

Photo: Amanda Dalbjorn
Specialized cells in the retina of the eye, rods and cones are responsible for our perception of light. The sticks are important mainly in low light conditions and do not play a big role in the perception of color, so we will focus on cones.
People usually have three types of cones. The presence of three different types of cones makes a person a “trichromat”. However, there is at least one confirmed case of human tetrachromat ! Other animals have even more cone species. We mantis - sixteen species.
Each type of cone is indicated by the wavelengths of light to which it responds. The standard designation is S, M and L (short, medium, long waves).

Three curves show how sensitive cones of a certain type are to each wavelength. The highest point of each curve is called the "peak wavelength", indicating the wavelength to which the cone is most sensitive.
Let's see how our cones process the light reflected from the lemon in the hand.
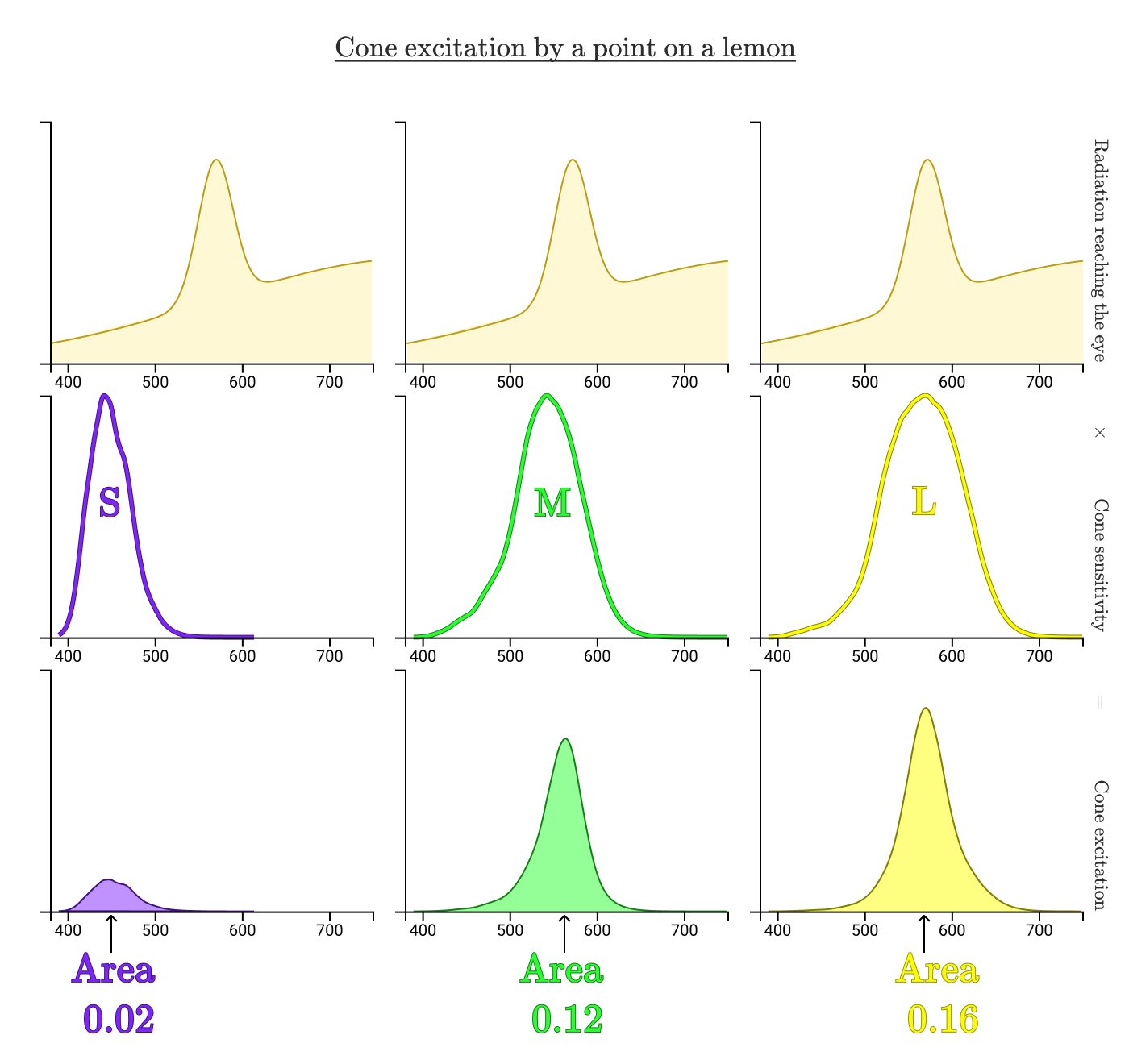
The areas bounded by the curves show how much of the radiation reflected from the lemon excites each type of cone. In this case, the normalized excitations of the cones S, M, and L are 0.02, 0.12, and 0.16, respectively. Now repeat the process for the lemon on the screen.

Despite completely different emission spectra, cone excitations are the same (S = 0.02, M = 0.12, L = 0.16). That's why a dot on a real lemon and a dot on a digital lemon look the same for us!
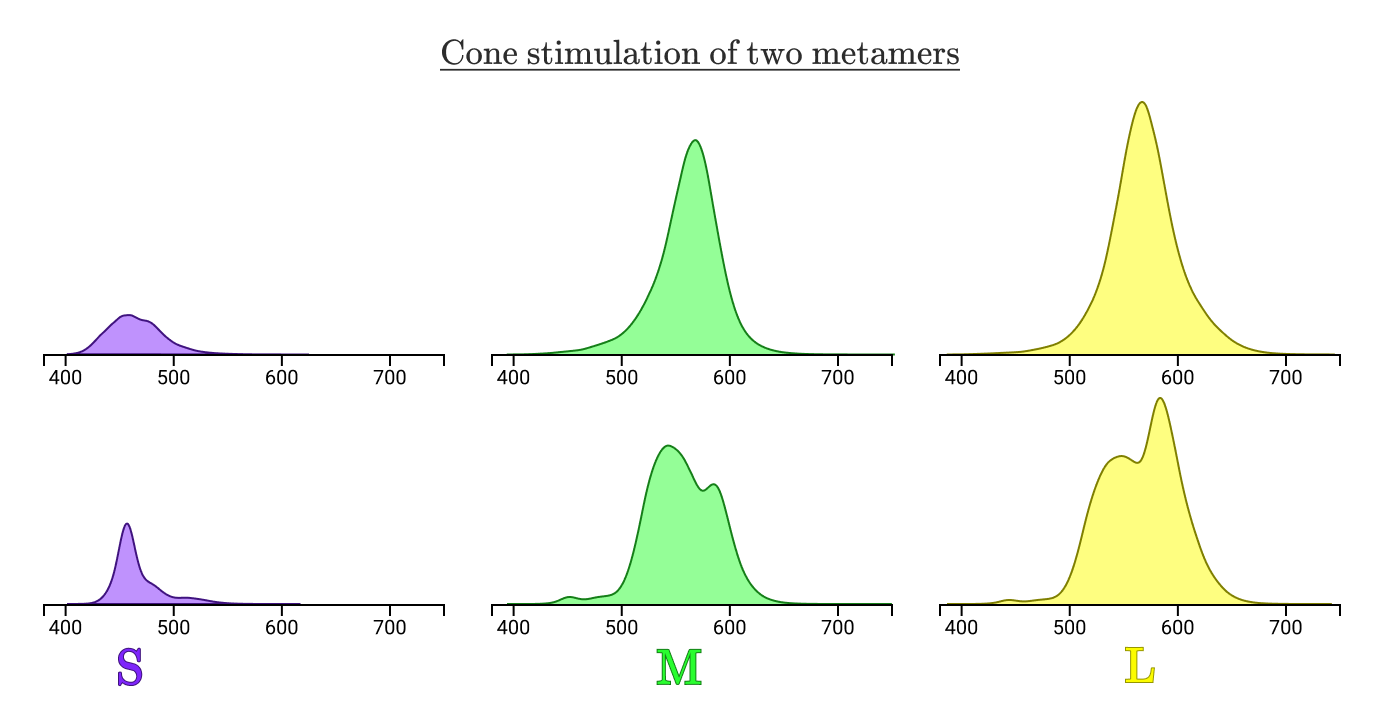
Metamers will always have a normalized area under the stimulation curves of three types of cones.
Our three sets of cones reduce any spectral flux density curve.
Triplet in reality
Color spaces
Color spaces allow you to quantify color. In the previous chapter, we saw that a specific yellow color can be represented as (0.02, 0.12, 0.16) in the SML color space, which is better known as the LMS color space .
Since this color space describes the stimulation of cones, by definition, any visible color of a person can be represented by the positive LMS coordinates (with the exception of extremely rare tetrachromat people who need four coordinates instead of three).
Unfortunately, this color space has some useless properties.
First, not all triplet values (also called color components or color coordinates) физически возможны. Например, координаты LMS (0, 1, 0). Чтобы выйти на эту координату, нужно как-то стимулировать колбочки М, при этом вообще не стимулируя колбочки L и S. Но это невозможно, потому что кривая чувствительности колбочек M значительно перекрывает L или S на всех длинах волн!

Любая длина волны, которая стимулирует колбочки M, также будет стимулировать колбочки типа L или S (или оба типа!)
В итоге возникает проблема, что реально сложно увеличить стимуляцию только одного типа колбочек. Из-за такого побочного эффекта, в частности, данная цветовая модель не очень совместима с производством дисплеев.
Another historical, practical problem is that the exact sensitivity of cones was not known until the 1990s, and the need to develop a mathematically accurate color model arose much earlier. The first significant progress in this area occurred in the late 1920s.
Wright and Guild Color Experiments
In the late 1920s, William David Wright and John Guild conducted experiments. They accurately identified individual colors by the contribution of three specific wavelengths.
Although they probably did not know about the three types of cones on the retina, but a hundred years before they came up with the idea that all visible colors can be represented as a combination of three colors.
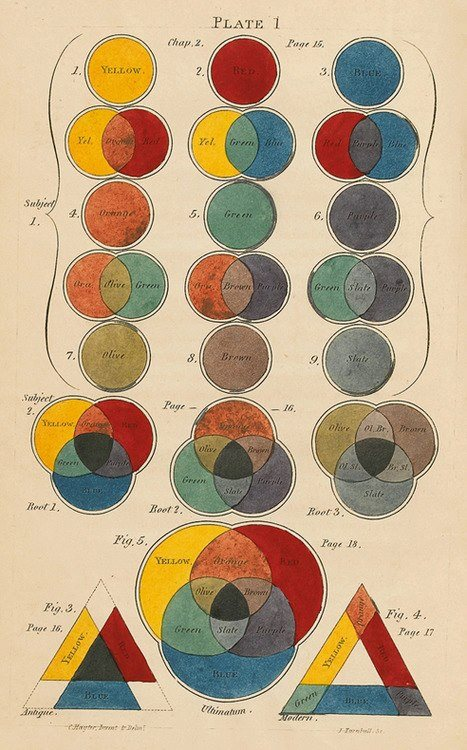
Charles Hayter’s tricolor color theory example, 1826.
Wright and Guild came up with the idea to build an apparatus that would allow subjects to determine test color as a combination of three light sources with a fixed wavelength. The setup looked something like this: The
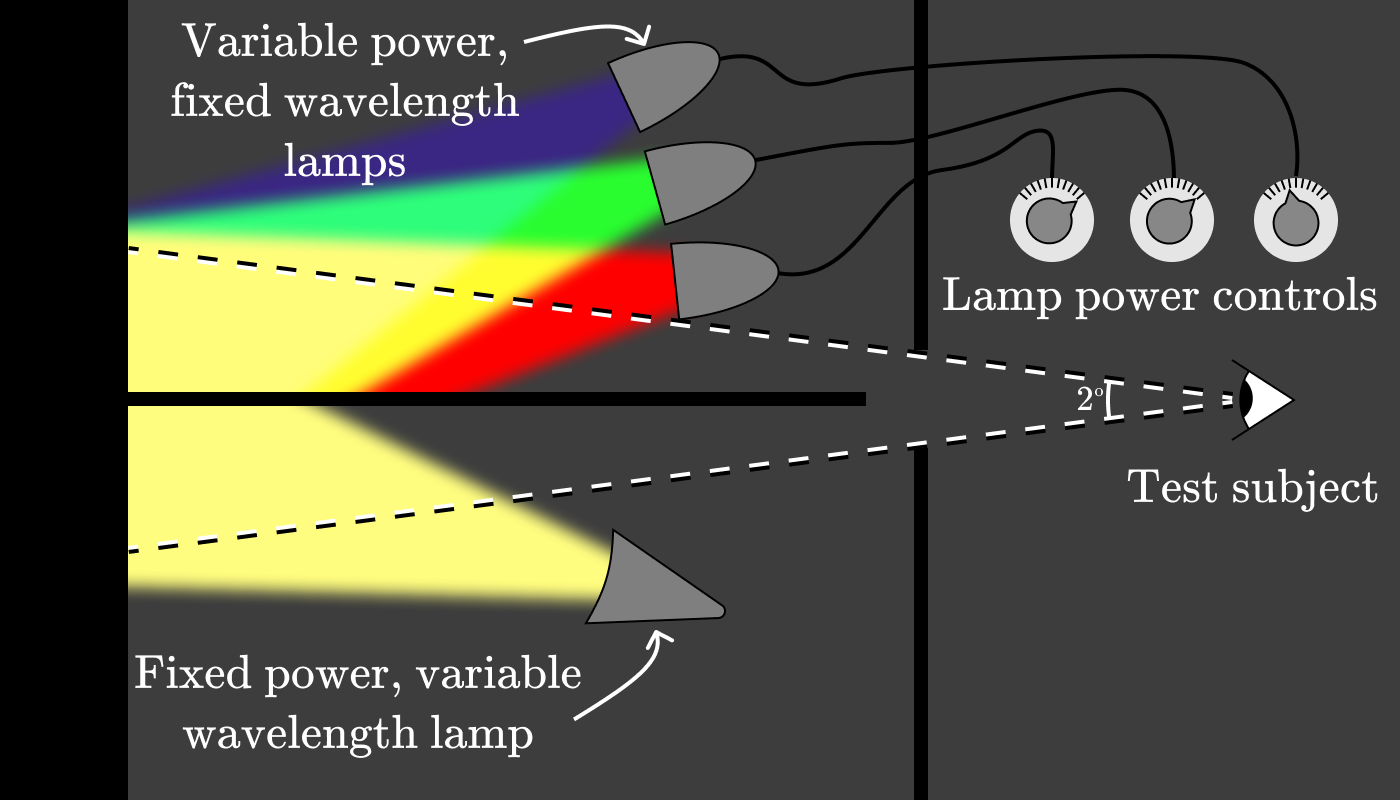
experimenter tuned the lamp below for a specific wavelength, (for example, 600 nm), and then asked the subjects to adjust the power of the three control lamps so that the color matches.
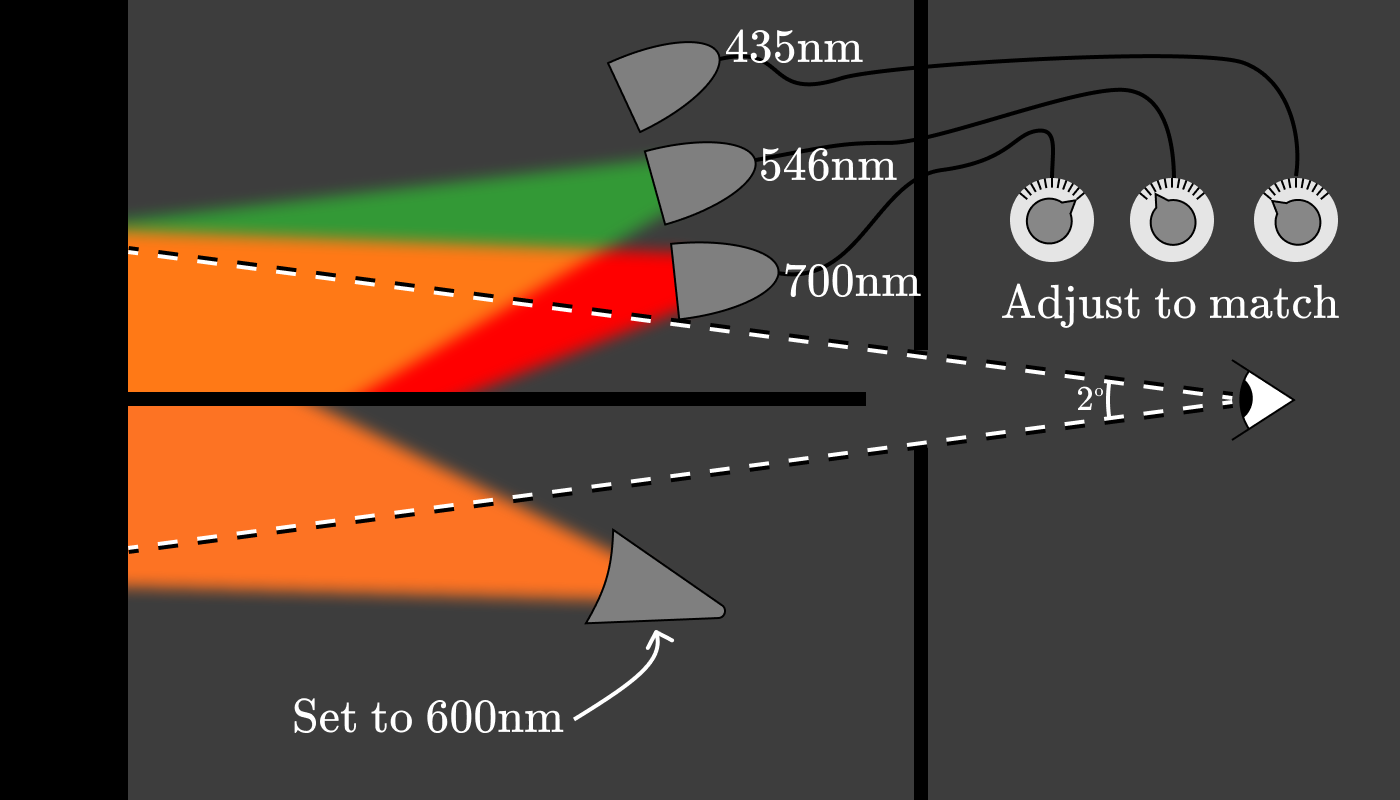
The power of each of the three lamps (red, green and blue) gives us a triplet of pure spectral colors, which corresponds to 600 nm. After repeating this experiment every 5 nm for approximately ten subjects, a graph was created showing the amount of red (700 nm), green (546 nm) and blue (435 nm) light needed to restore the appearance of the color at a given wavelength. Functions are known as color matching functions (CMFs) .
These specific color addition functions are known as
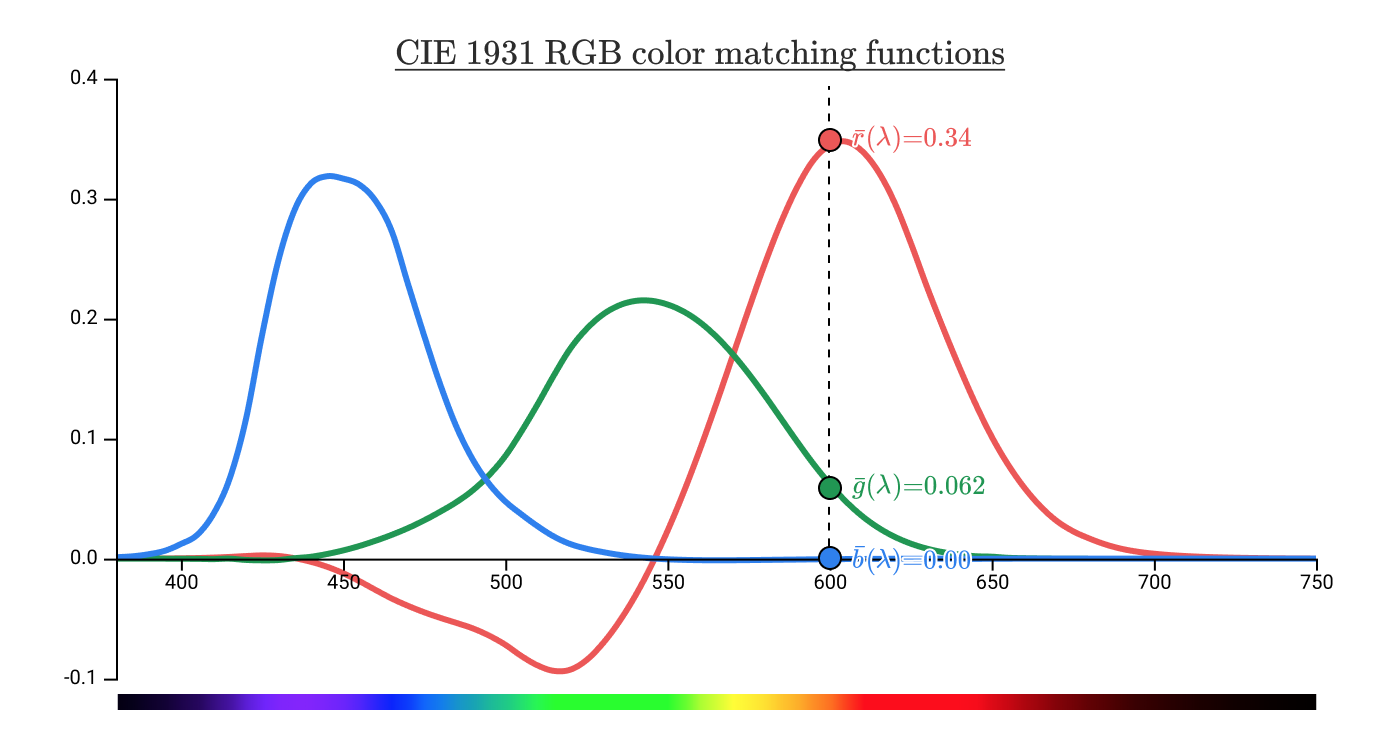
They give a clear spectral color, which is associated with a wavelength of 600 nm in
Wait, what do the negative values of the function mean?
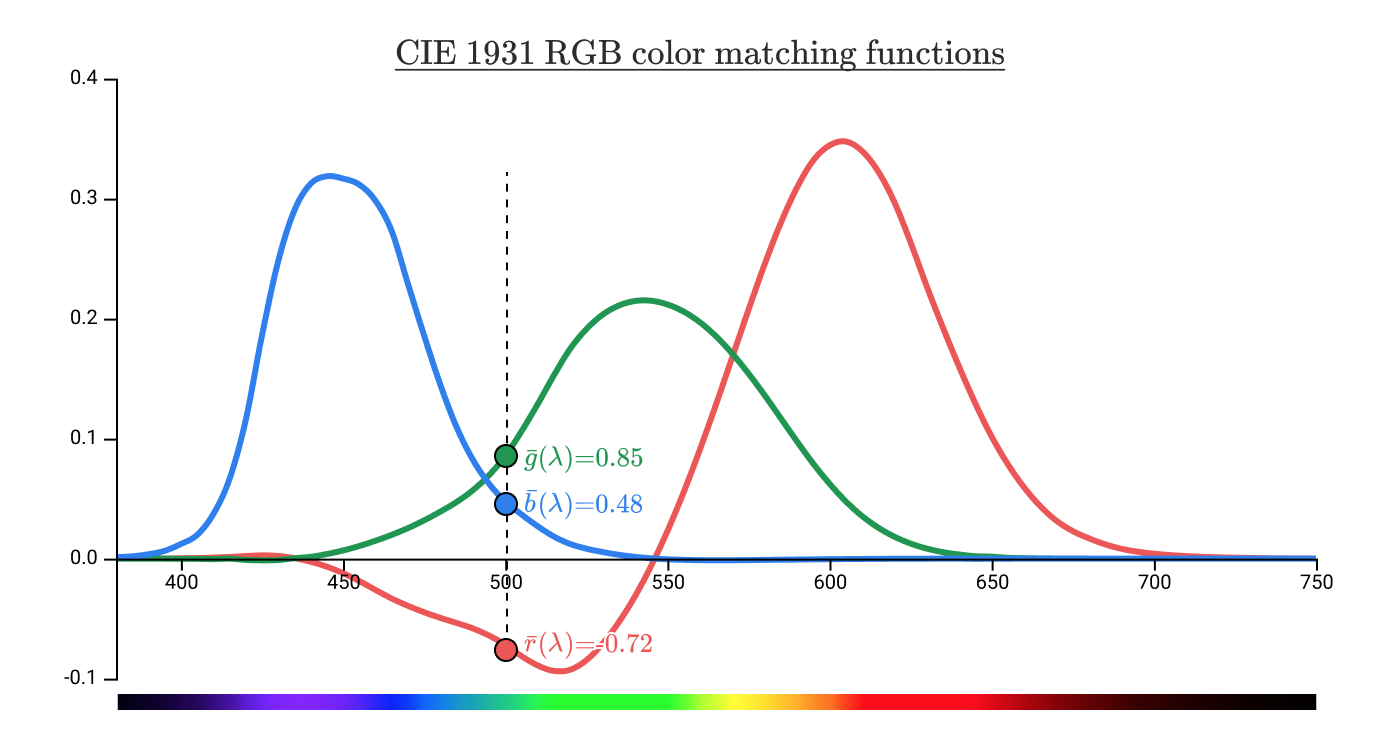
In pure spectral colors, which are associated with a color at a wavelength of 500 nm, the coordinates
It turns out that no parameters of the red (700 nm) lamp at the top make it possible to match the color of 500 nm at the bottom, regardless of the power of the blue and green lamp at the top. But you can achieve a match on both sides by moving the red lamp down .
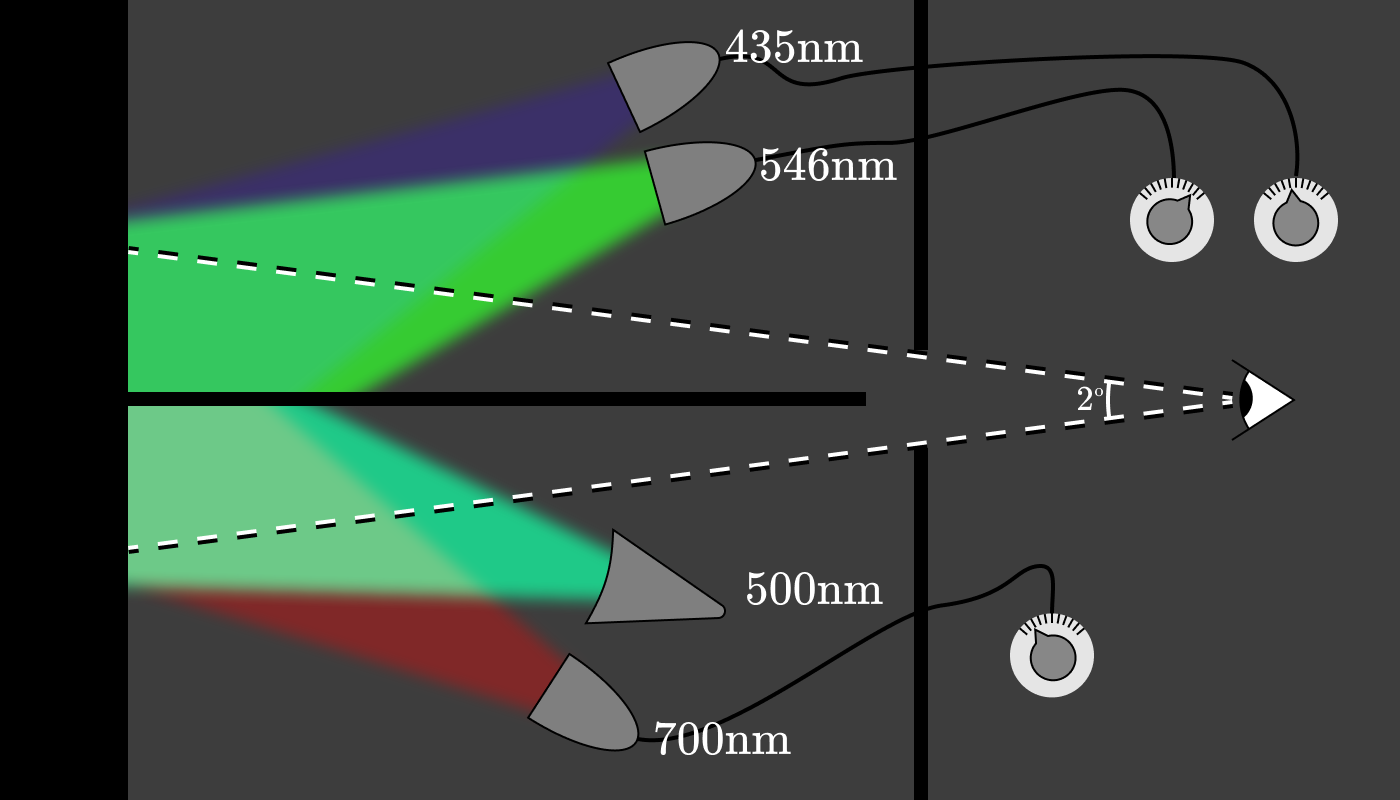
In a real experimental setup, probably, a complete set of lamps with fixed wavelengths was installed at the top and bottom to regulate each of them in the “negative” zone.
Using our color-combining functions, you can find a match for any monochromatic light by combining (possibly negative) the amount of red (700 nm), green (546 nm) and blue (435 nm) light.
The color addition functions can be analyzed in the same way as we analyzed the sensitivity of the L, M, and S cones. Take the same lemon color:
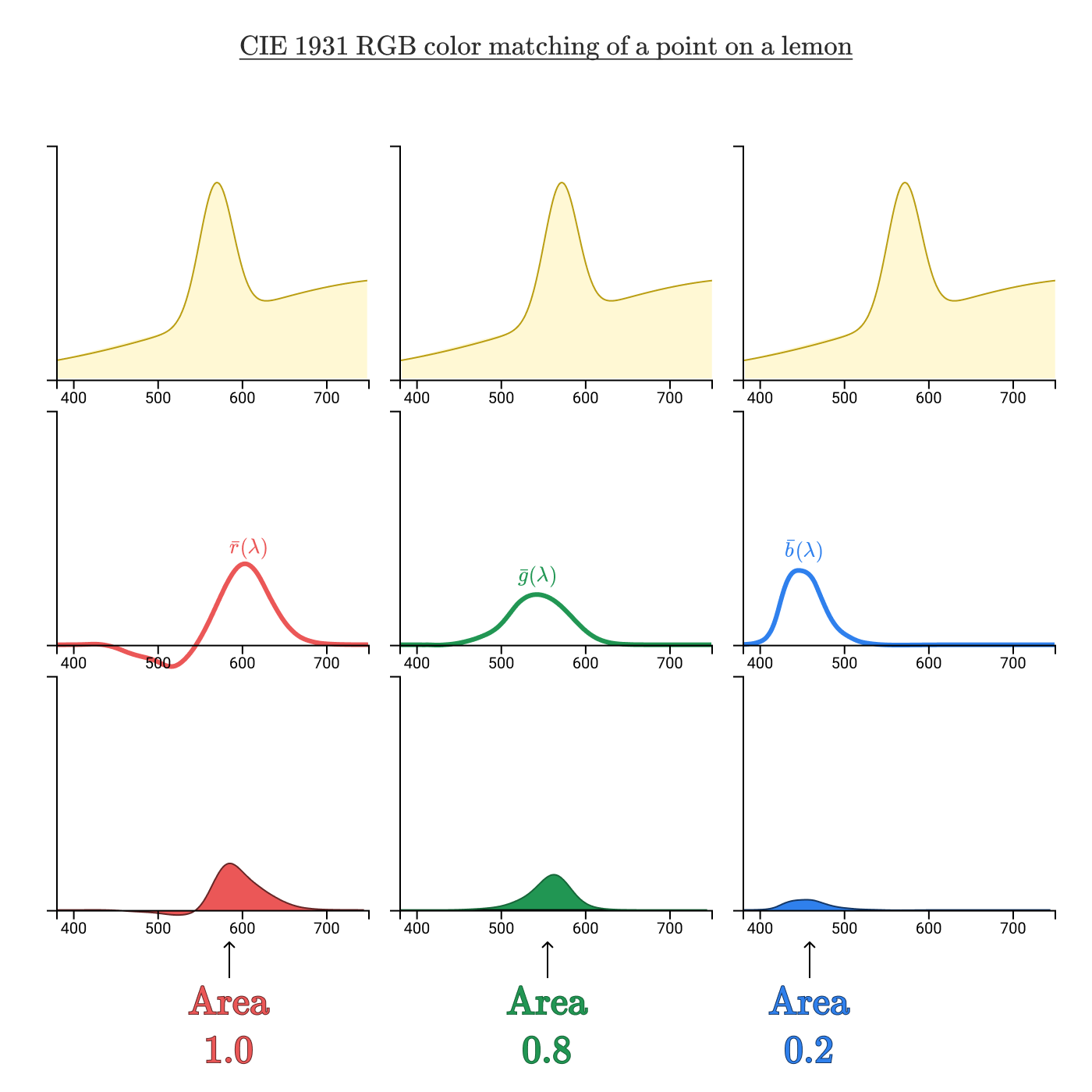
Taking the regions bounded by the product curves of the spectral curve and color addition functions, we got an RGB triplet (1,0, 0, 8, 0,2), which uniquely identifies this color.
While the color space
But this graph only shows which spectral colors cannot be reproduced. What about non-spectral colors? Is it possible to produce pink color with a combination of R, G, B? Or cyan (blue-green color)?
To answer these questions, we need a better way to visualize color space.
Visualization of color spaces and chromaticity
So far, in most diagrams, we have arranged wavelengths along the horizontal axis, placing several graphs one after another in the same plane.

Instead, you can represent color as a function

Cool! A wider range of colors is displayed here, not just the spectral colors of the rainbow.
To reduce to two dimensions, it is easiest to make separate diagrams for each pair of values, for example:
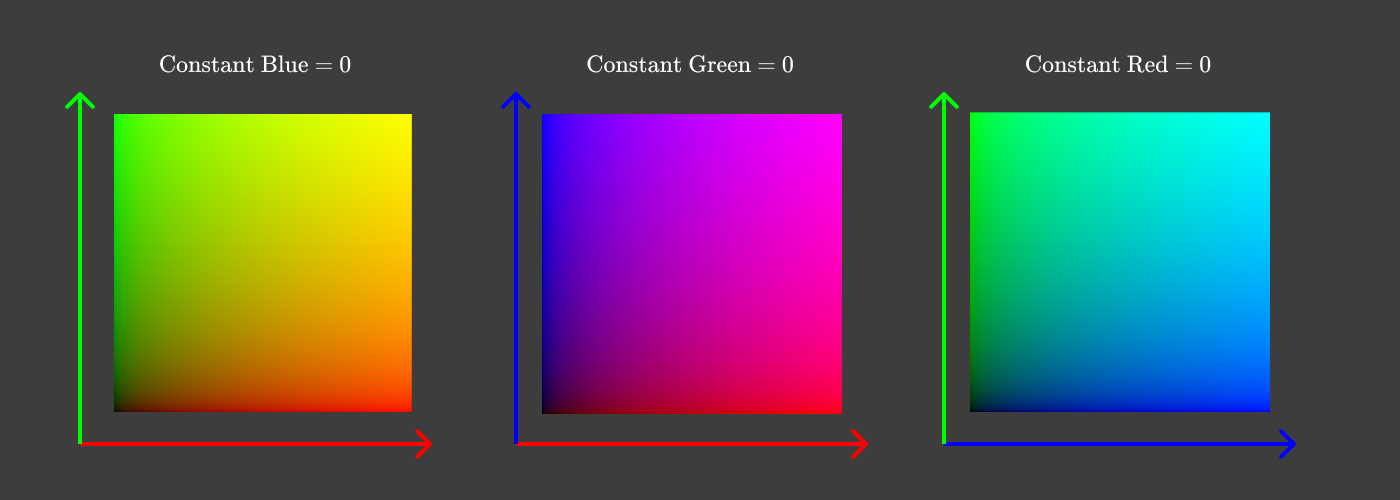
Pairs of components with a zero third component
On each of the diagrams, we discarded one dimension, zeroing out one of the three color components. But instead of fixing the red, green or blue components, it would be more convenient to see all the colors, fixing the lightness .
Looking again at the cube, we see that (0, 0, 0) corresponds to black, and (1, 1, 1) to white.

What happens if we cut the cube diagonally through a plane containing
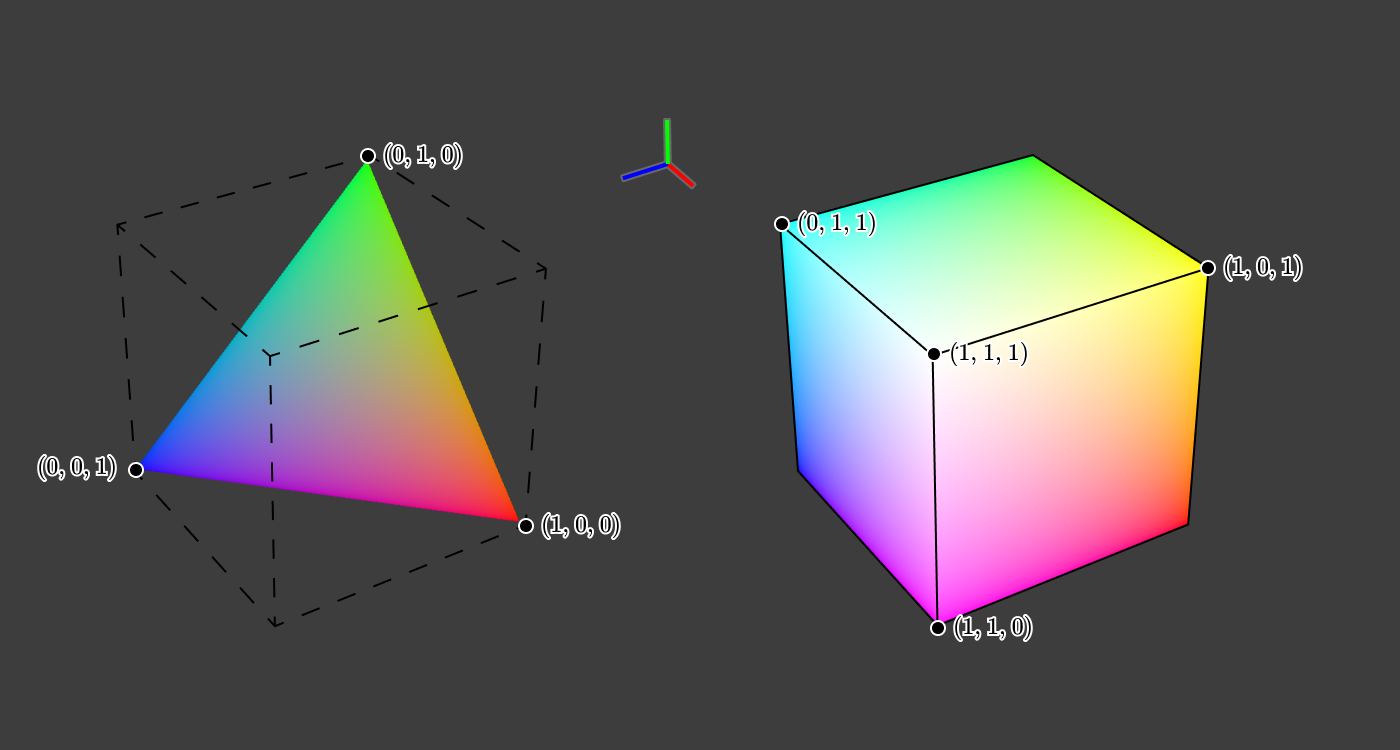
This triangular slice of the cube has the property that
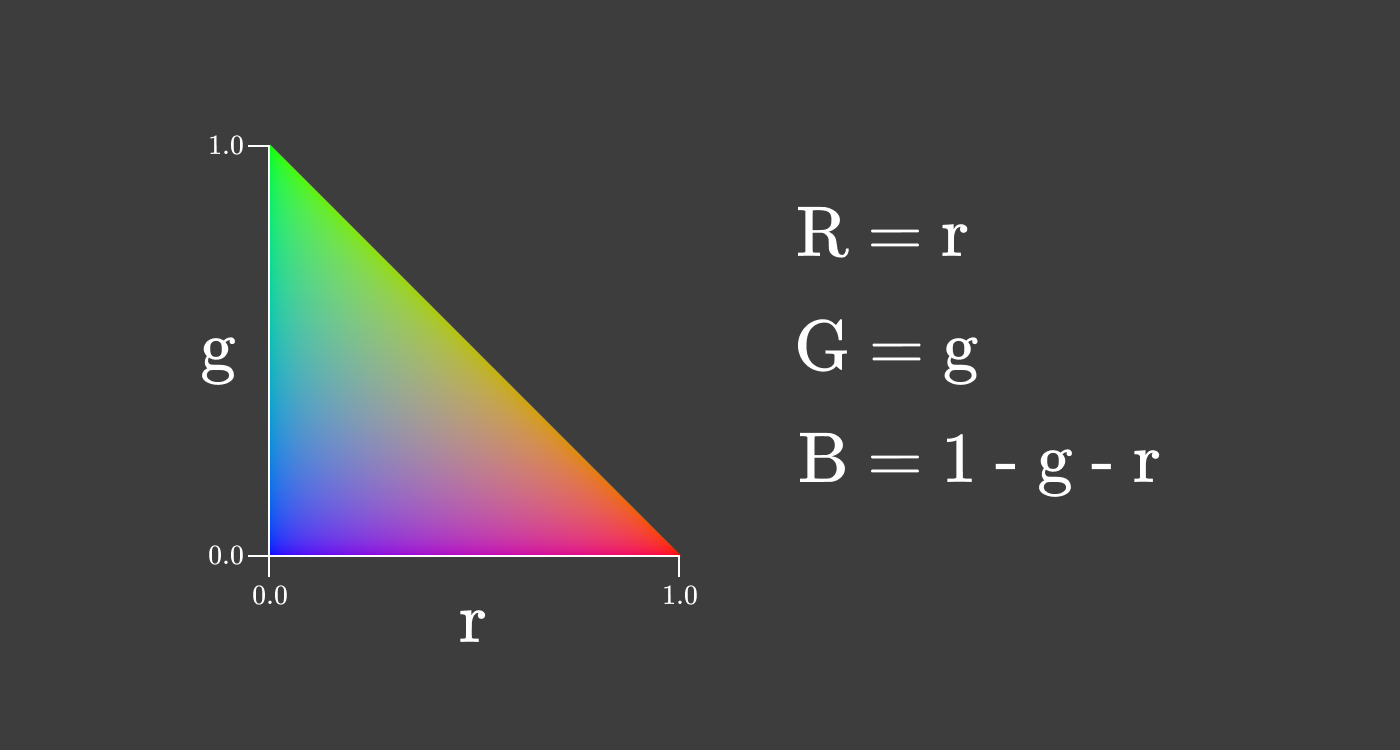
This two-dimensional representation of color is called chromaticity . This particular species is called rg-chromaticity . Chromaticity provides information on the ratio of primary colors, regardless of lightness.
This means that the same chromaticity can be maintained at different levels of lightness.
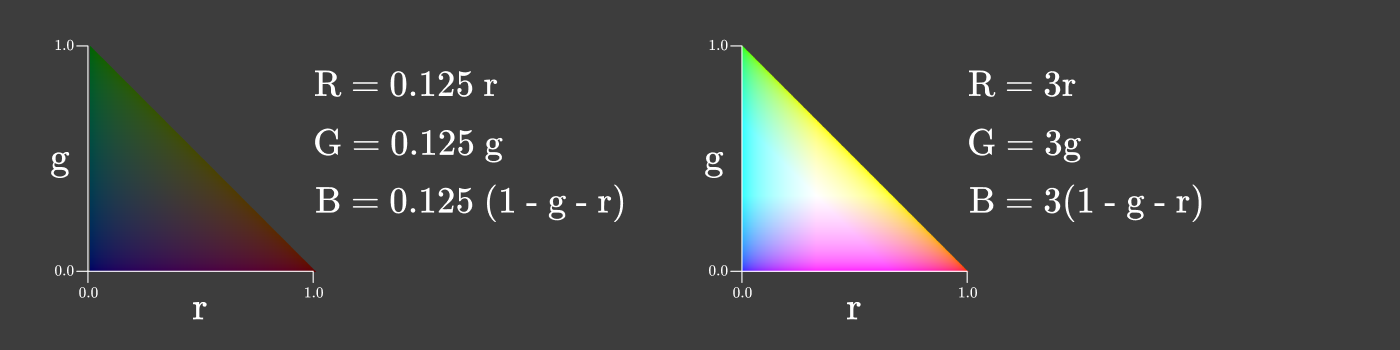
You can even make a chromaticity diagram where the intensity changes along with r and g in order to maximize the intensity while maintaining the relationship between R, G and B.
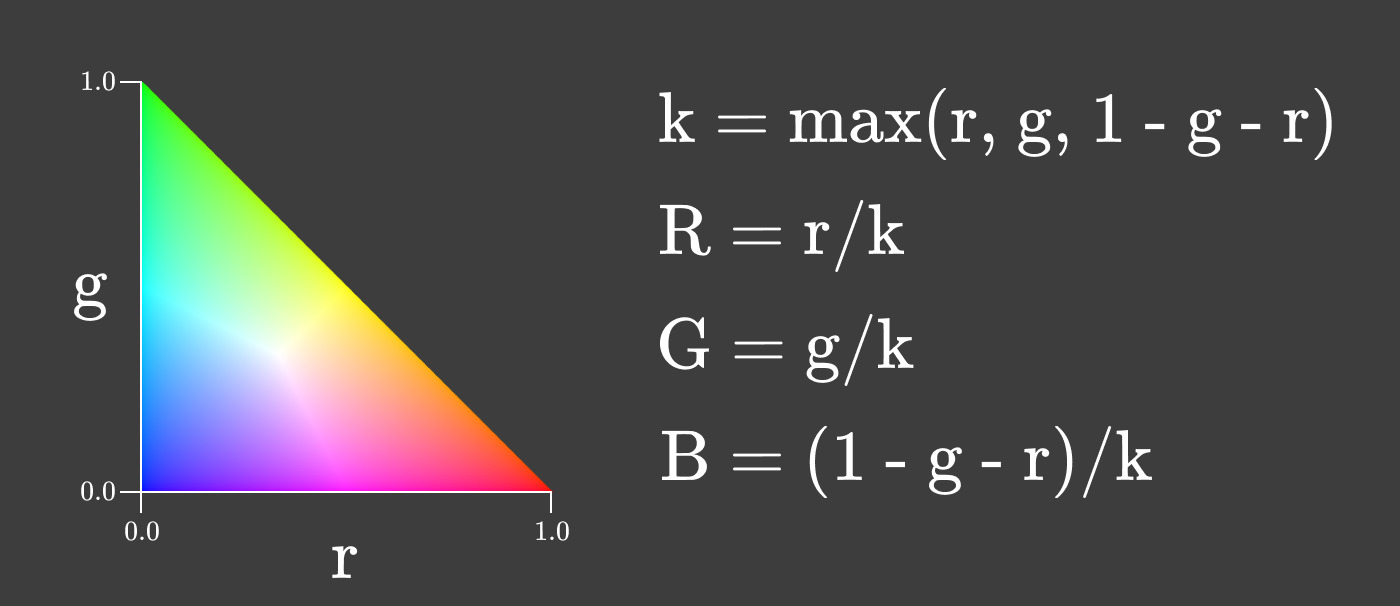
Chromaticity is a useful property of color, because it does not change when the intensity of the light source changes, as long as the source has the same spectral composition. When the brightness of the screen changes, the chromaticity remains constant!
There are many ways to divide chromaticity into two dimensions. One common method is used in HSL and HSV color spaces. In both color spaces, chromaticity is divided into “hue” and “saturation”:
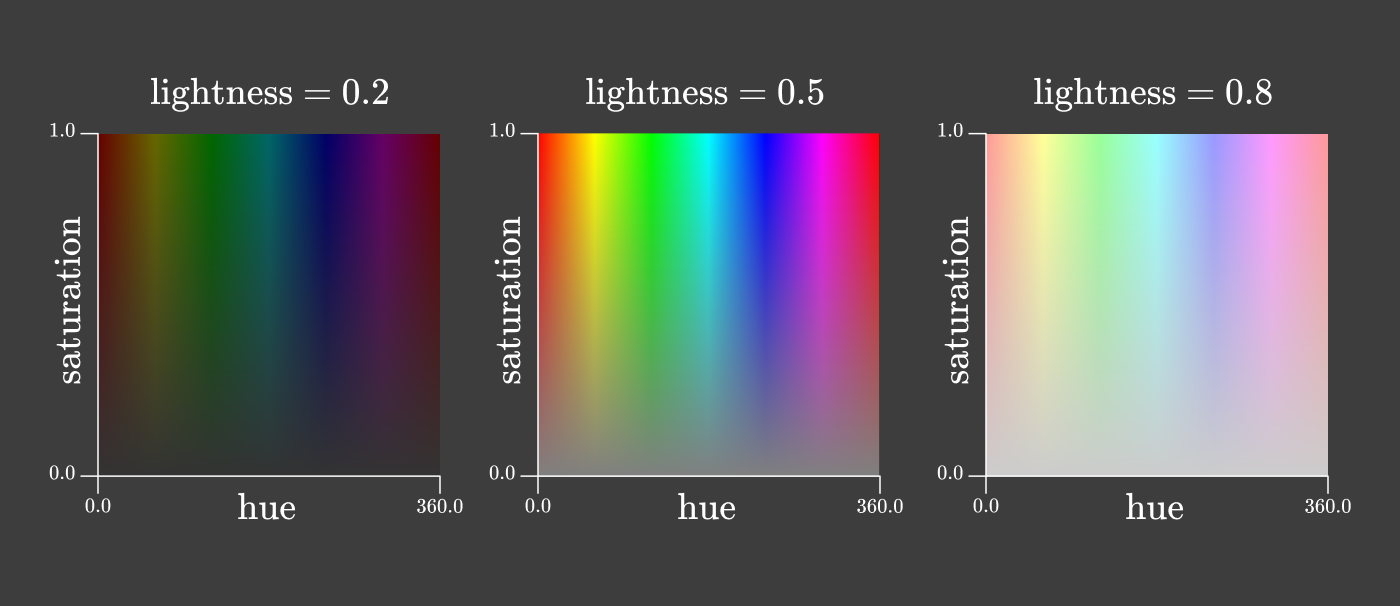
At first glance, it might seem that the rg chromaticity triangle and these hue / saturation squares contain all the colors of the rainbow. Well, it's time to get back to those annoying negative values in the color addition functions.
Gamma and spectral locus
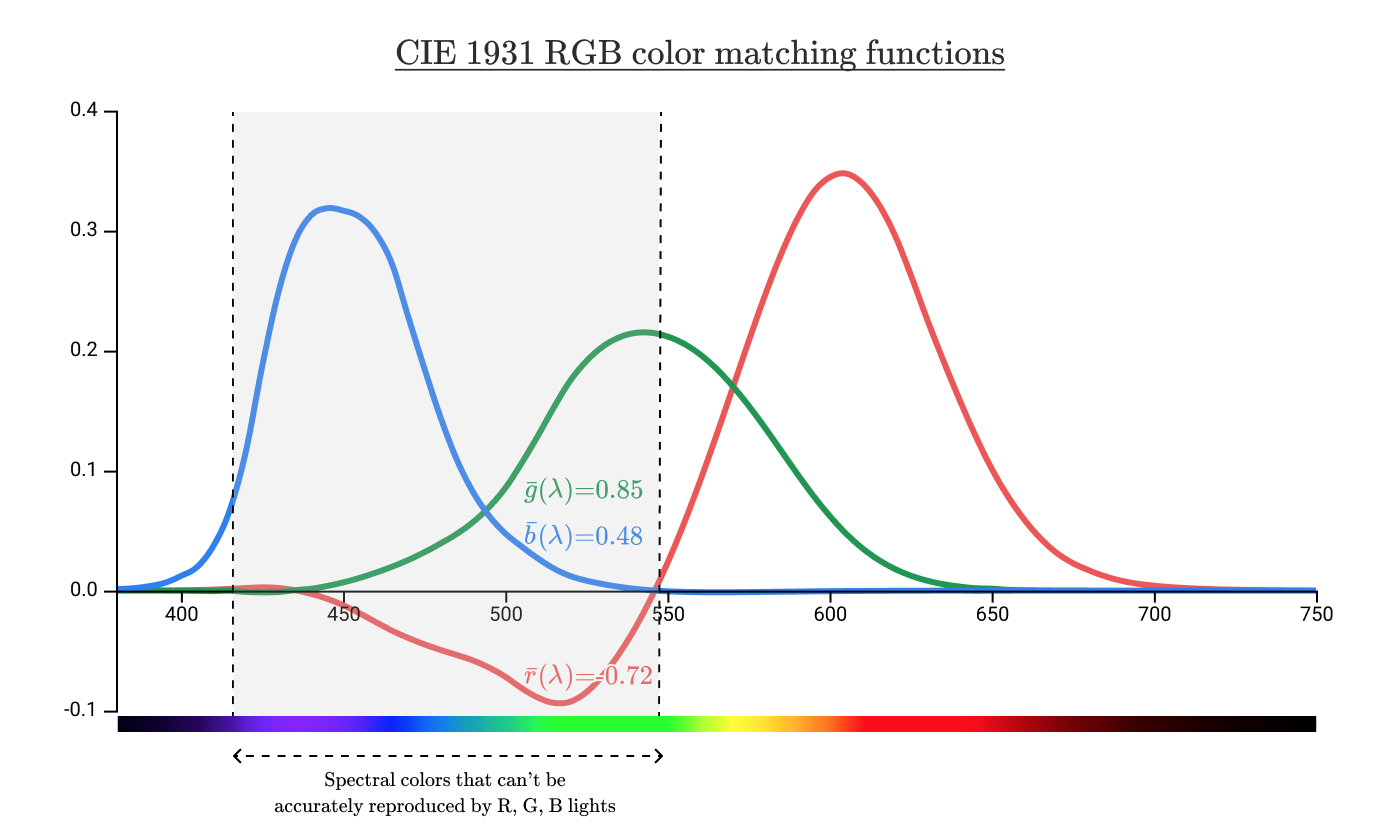
If we take our color addition functions
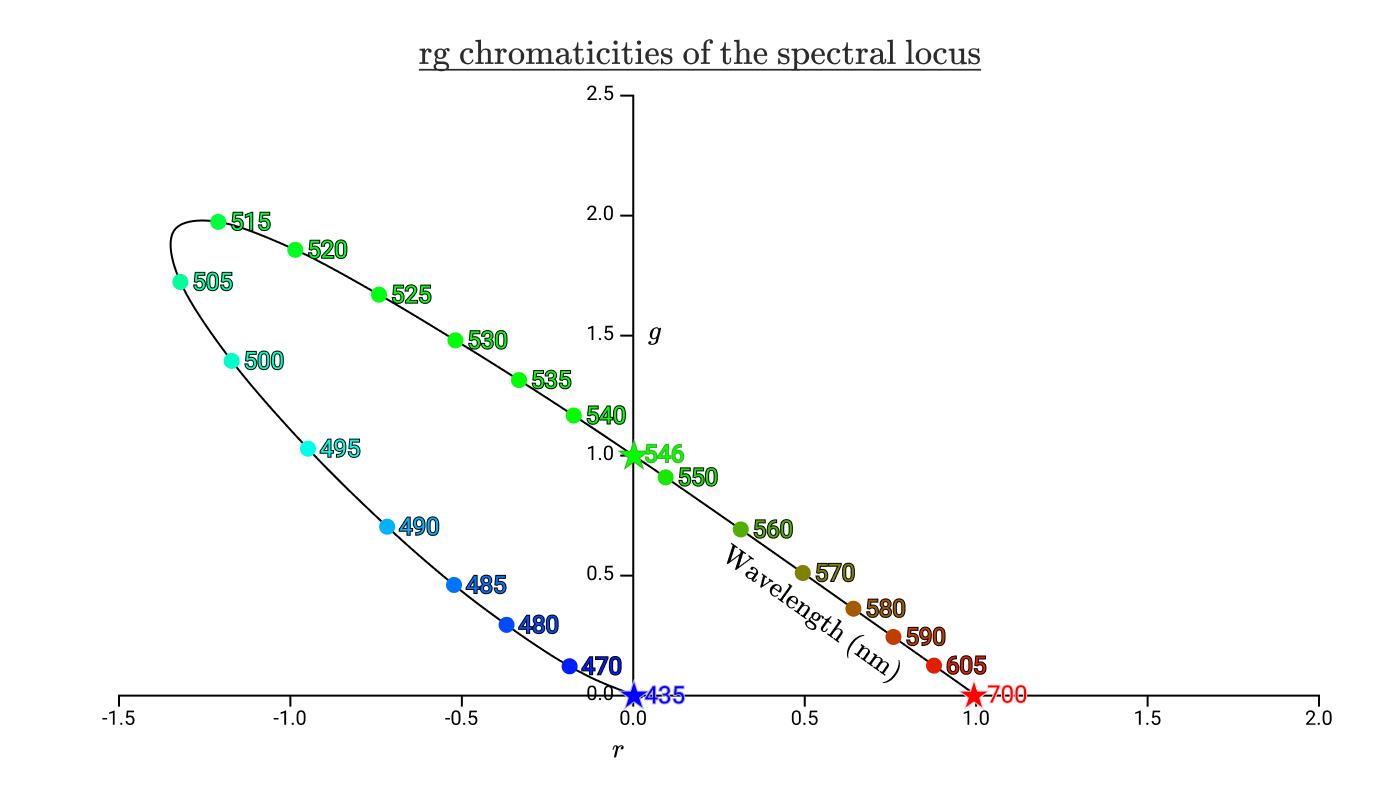
black curve with colored dots shows the chromaticity of all pure spectral colors. The curve is called the spectral locus . The asterisks correspond to the wavelengths in the lamps used in the color addition experiments.
Put the previous chromaticity triangles on this diagram.
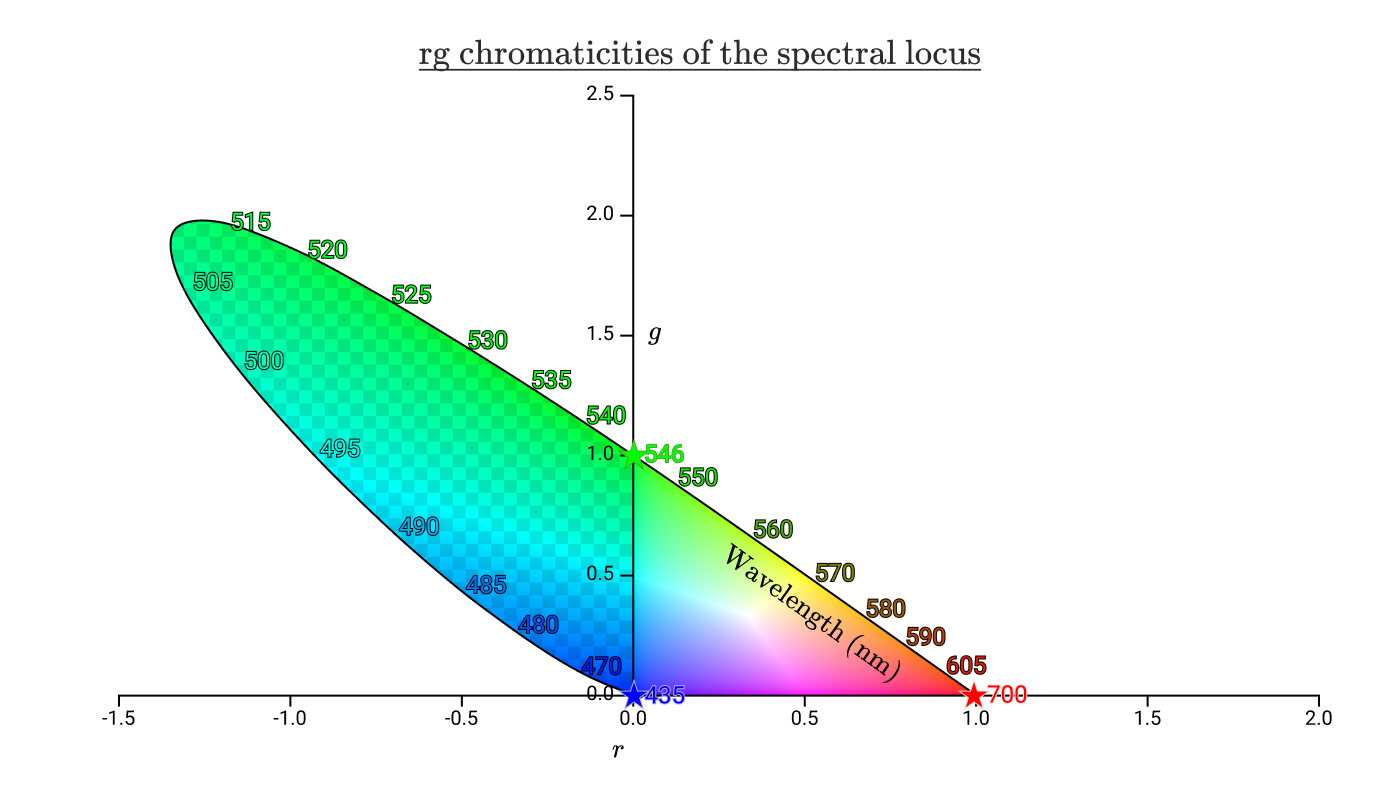
The region inside the spectral locus contains all the colors visible to humans. The checkered area shows the colors that a person perceives, but they cannot be reproduced by adding waves of 435 nm, 546 nm and 700 nm. It can be seen from this diagram that we cannot reproduce any of the spectral colors between 435 nm and 546 nm, including pure cyan.
The triangle to the right without checkers is all the colors that can be reproduced by positive values of R, G, B. We call this area the gamut of color space.
Before finally returning to the hexadecimal codes, you need to consider another color space.
CIE XYZ color space
In 1931, an International Lighting Commission was convened. She set two color spaces. The first is the RGB color space that we already discussed, created from Wright and Guild’s color-combining experiments. The second was the XYZ color space.
One of the tasks of the XYZ color space is to obtain positive values for all colors visible to humans, so that all chromaticity values are in the range [0, 1] on both axes. For this, we carefully selected a suitable linear transformation of the RGB space.
An analog of rg-chromaticity in XYZ space is xy-chromaticity, and chromaticity diagrams are placed in a more standard coordinate system.
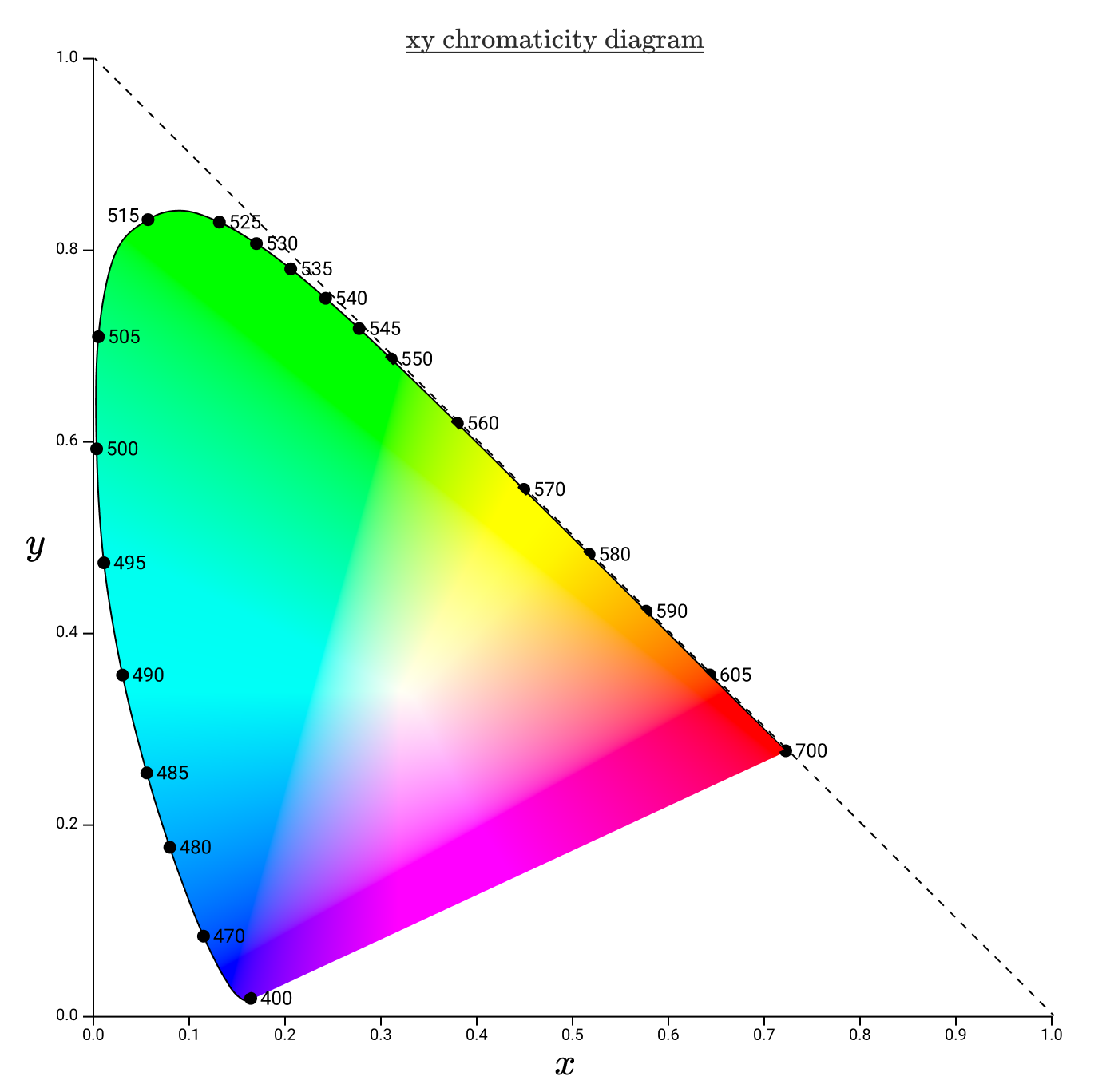
Gammas are usually represented by triangles in the xy-chromaticity diagram. For example, here's the CIE RGB gamut again, this time in xy space.
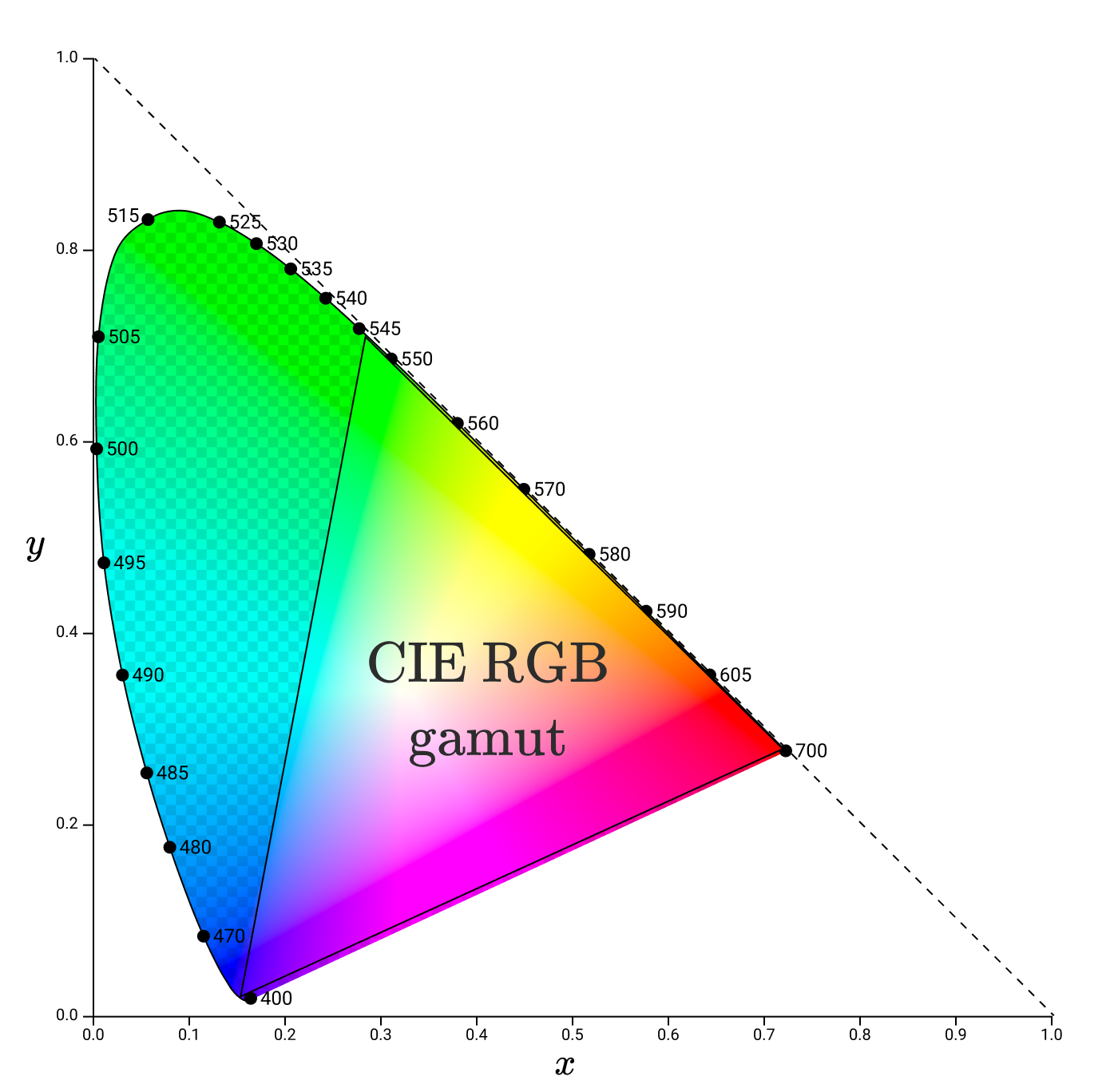
Having understood gamma & chromaticity, we can finally begin to discuss how digital displays are able to show the right colors.
Screen subpixels
Regardless of the manufacturer of the display, under a strong magnifying glass you will see a grid of pixels, where each pixel consists of three subpixels: one red, one green and one blue. It may look something like this:
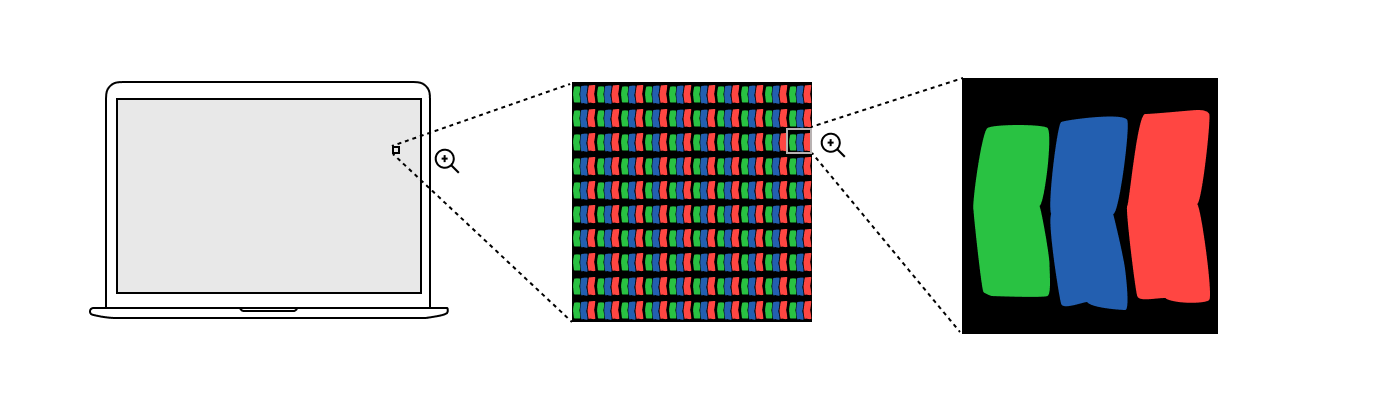
Unlike the lamps in the color addition experiment, subpixels do not emit monochromatic light. Each type of subpixel has its own spectral distribution, different for different monitors.
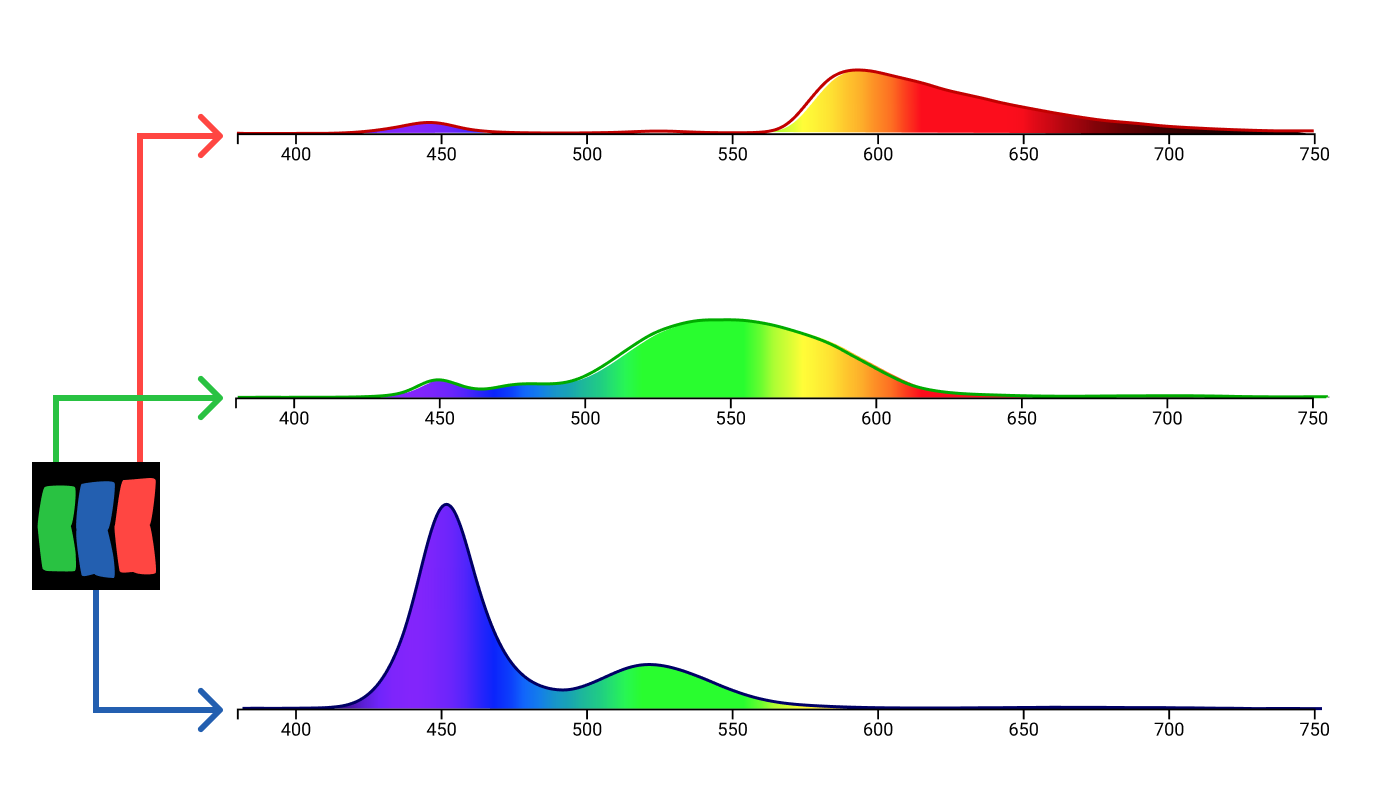
MacBook Air subpixel spectral data from f.luxometer
Using the ColorSync utility, I determined the gamma in the xy space for the display of my Macbook Pro.
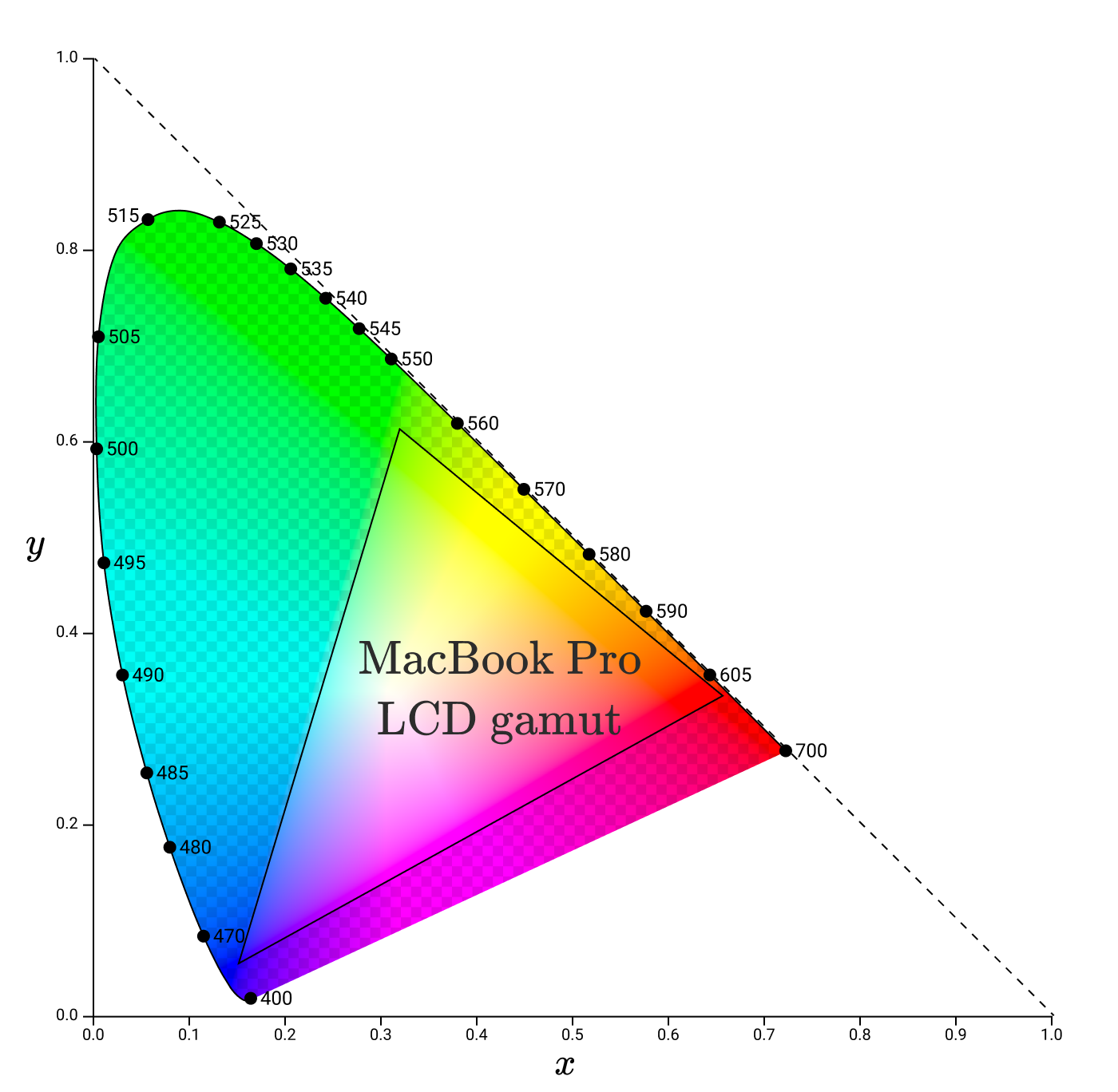
Note that gamma angles no longer lie along the spectral locus. It is understandable, because subpixels do not emit pure monochromatic light. This gamut represents the full color spectrum of the primary colors that this monitor can accurately reproduce.
While the gamut of monitors will vary, modern monitors should try to cover a certain different gamut: sRGB.
sRGB
sRGB (“standard red green blue”) is the color space created by HP and Microsoft in 1996 to accurately transmit color information between different devices.
The standard defines the chromaticity of primary colors.
| Chromaticity | Red | Green | Blue |
|---|---|---|---|
| x | 0.6400 | 0.3000 | 0.1500 |
| y | 0.3300 | 0.6000 | 0,0600 |
| Y | 0.2126 | 0.751 | 0,0722 |
If you apply them to the color space, you get a gamut similar to the gamut of the MacBook LCD screen, but a little less.
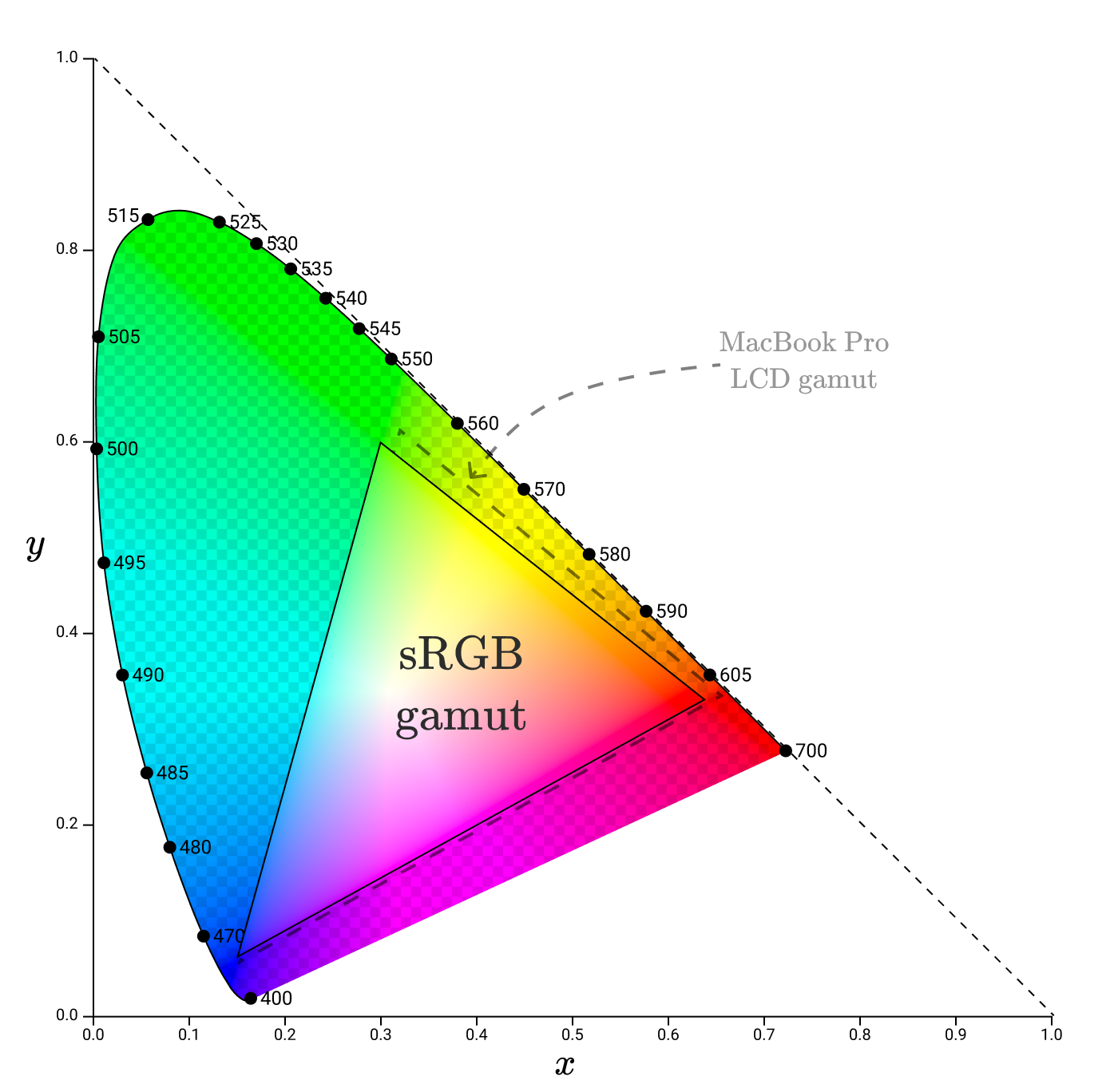
Some parts of the official sRGB gamut are not part of the MacBook Pro LCD gamut, meaning the display cannot reproduce them accurately. For this, the MacBook seems to use a modified sRGB gamut.
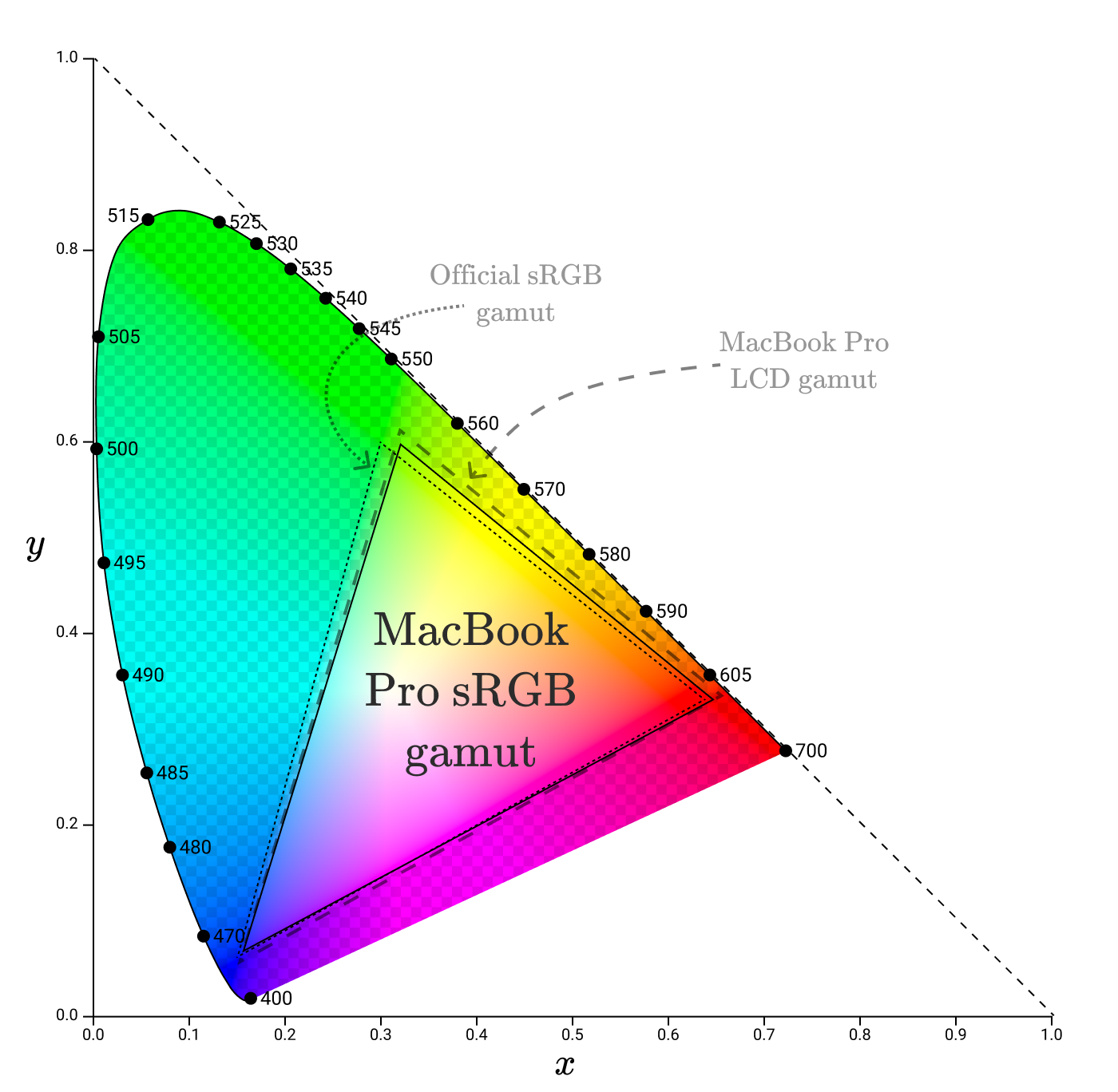
sRGB is the default color space that is used almost everywhere. This is the standard color space for browsers ( specified in the CSS standard ). All diagrams in this article are in the sRGB color space. This means that all colors outside the sRGB gamut are not correctly reproduced in the diagrams!
Which brings us finally to the color codes on the Internet.
Hexadecimal sRGB codes
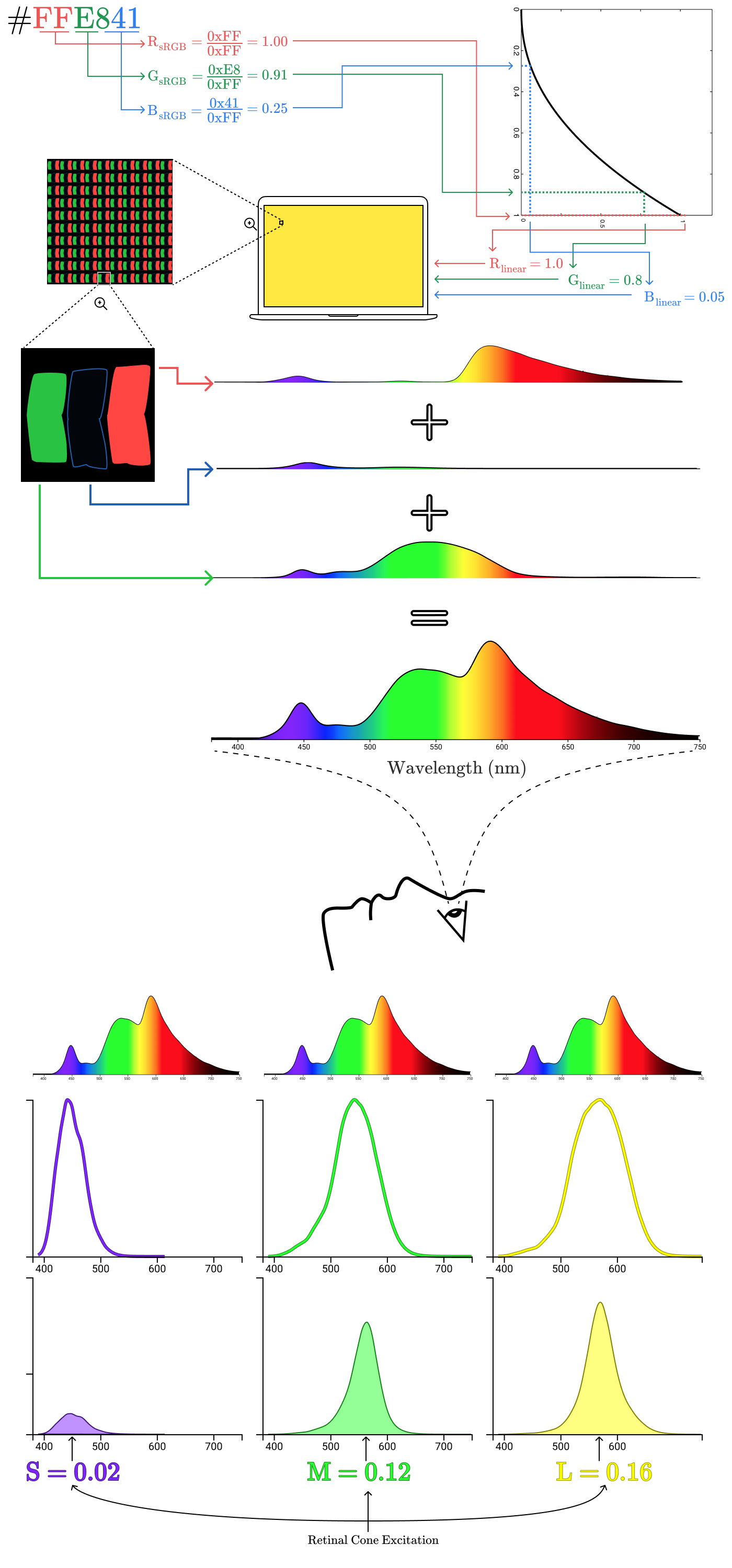
#9B51E0sets the color in sRGB space. To convert it to the corresponding coordinates (R, G, B), we divide each of the three components by 0xFF, that is, by 255. In this case:
Therefore, the coordinates will correspond to the color # 9BE1E00x9B / 0xFF = 0.61
0x51 / 0xFF = 0.32
0xE0 / 0xFF = 0.88Before sending these values to the display to set the intensity of the subpixels, you need to perform one more step: gamma correction.
Gamma correction
If each coordinate in the RGB space has 256 possible values, then I would like to make sure that each pair of neighboring coordinates is as different as possible from each other. For example, that
#030000different from #040000how #F40000from #F50000. Human vision is much more sensitive to small changes in weak light than strong light, so it is advisable to place more of these 256 values in the area of weak light.
Imagine that we want to encode shades of gray, but we only have three bits for this, which gives eight possible values.
If we construct the values of gray as a linear function of energy, then it will look something like this:

Let's call it a three-bit value
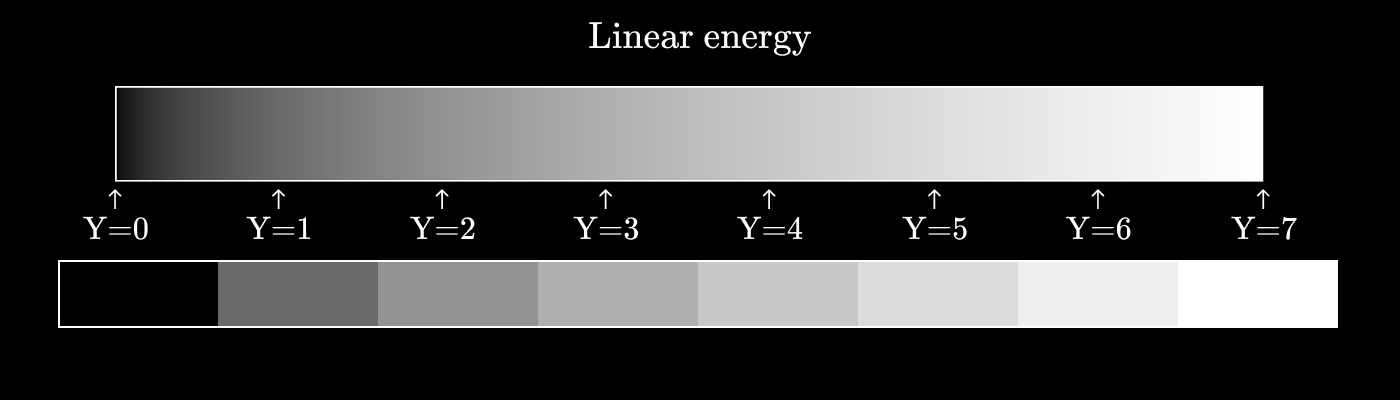
As you can see, the difference in perception between
Now let's see what happens if you use a power function instead. Let's try
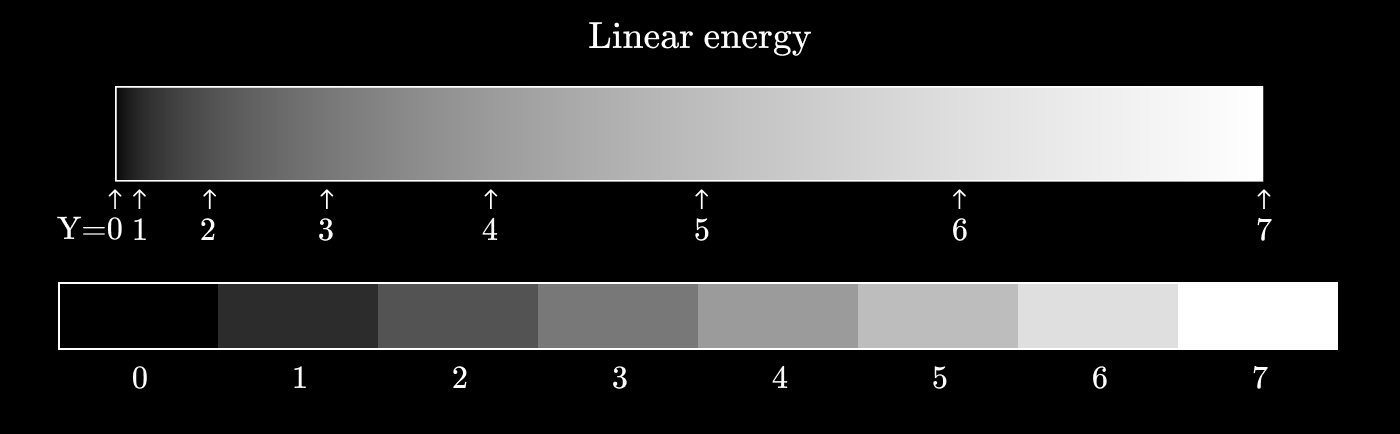
We have become much closer to uniformity of perception, so that each neighboring pair of values differs to the same extent as any other neighboring pair.
This conversion of energy values to discrete values is called gamma coding . The inverse operation (conversion of discrete values to energy) is called gamma decoding .
In general, gamma correction is performed according to the formula
The coding and decoding rules for sRGB are based on a similar idea, but the formula is a bit more complicated.
If we construct sRGB values relative to linear values, we get the following graph:
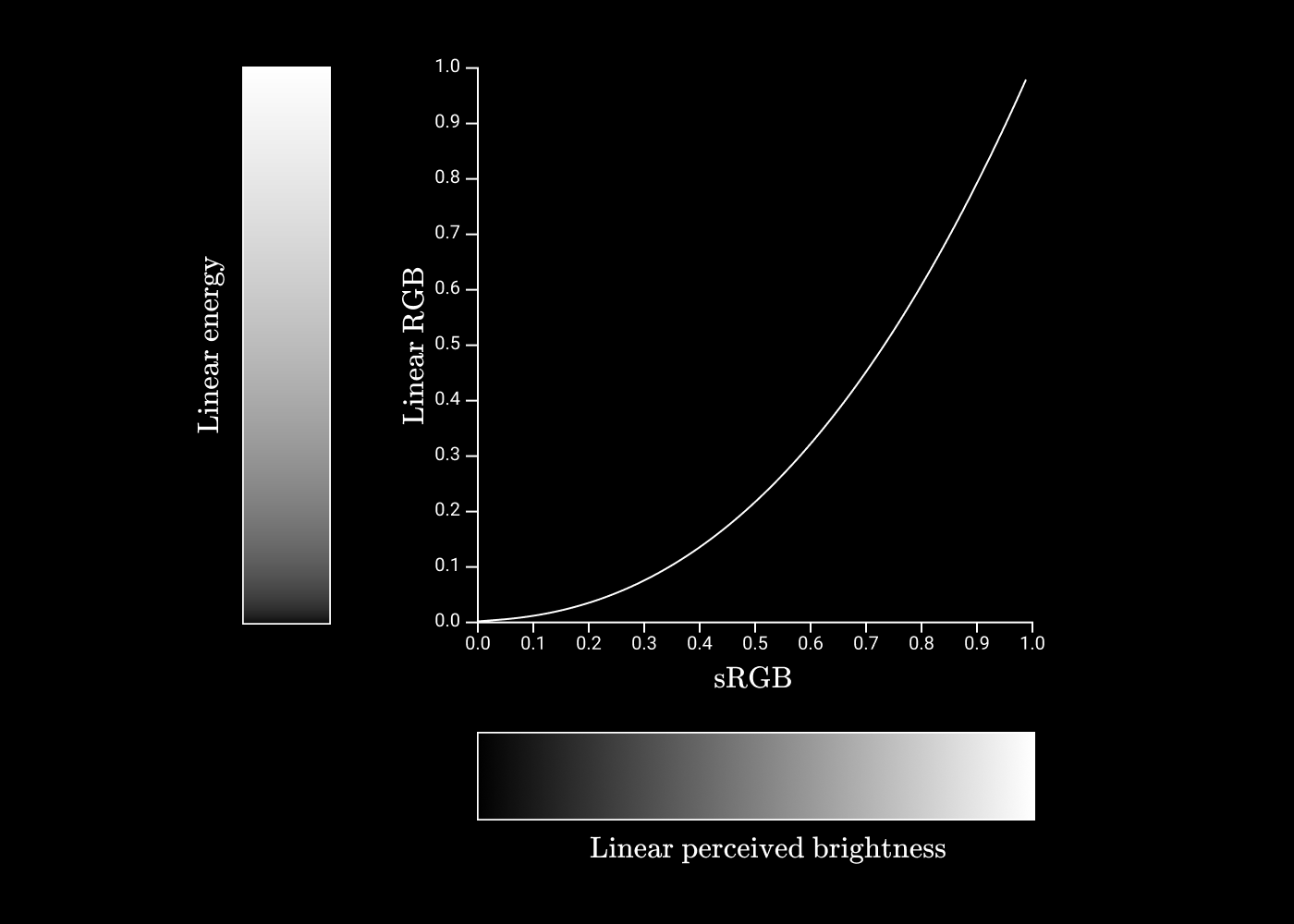
Great! This is the last piece of the puzzle to understand how we move from hexadecimal codes to eye perception! We will make a step-by-step guide.
From hexadecimal codes to the eye
First, we take
#9B51E0, divide into components R, G, B and normalize these components in the range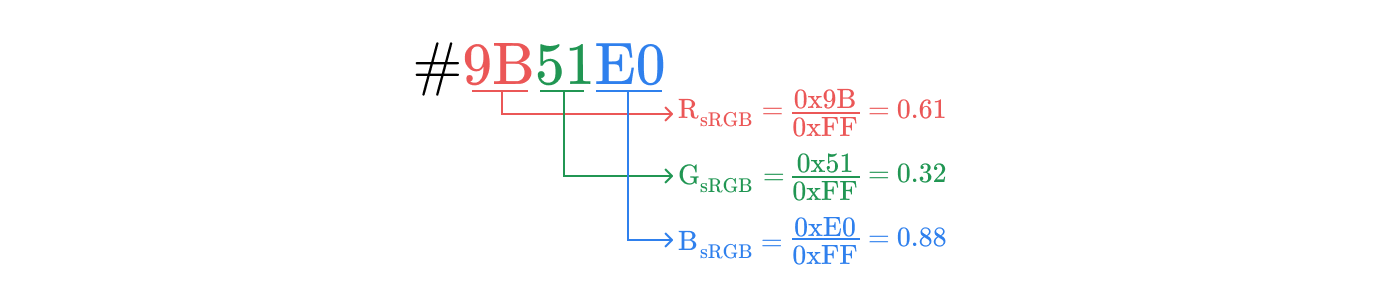
It gives us a coordinate
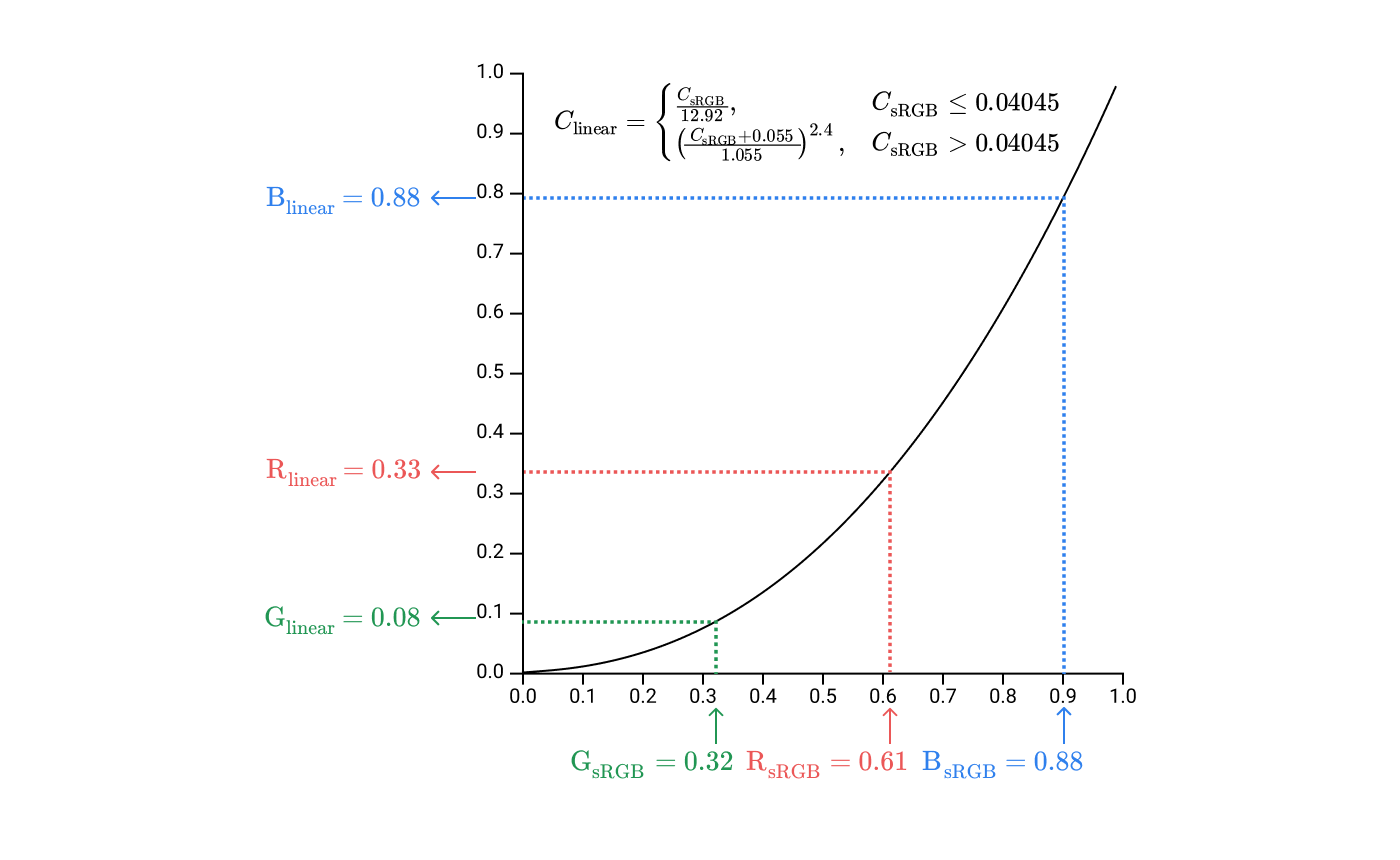
It gives us a coordinate
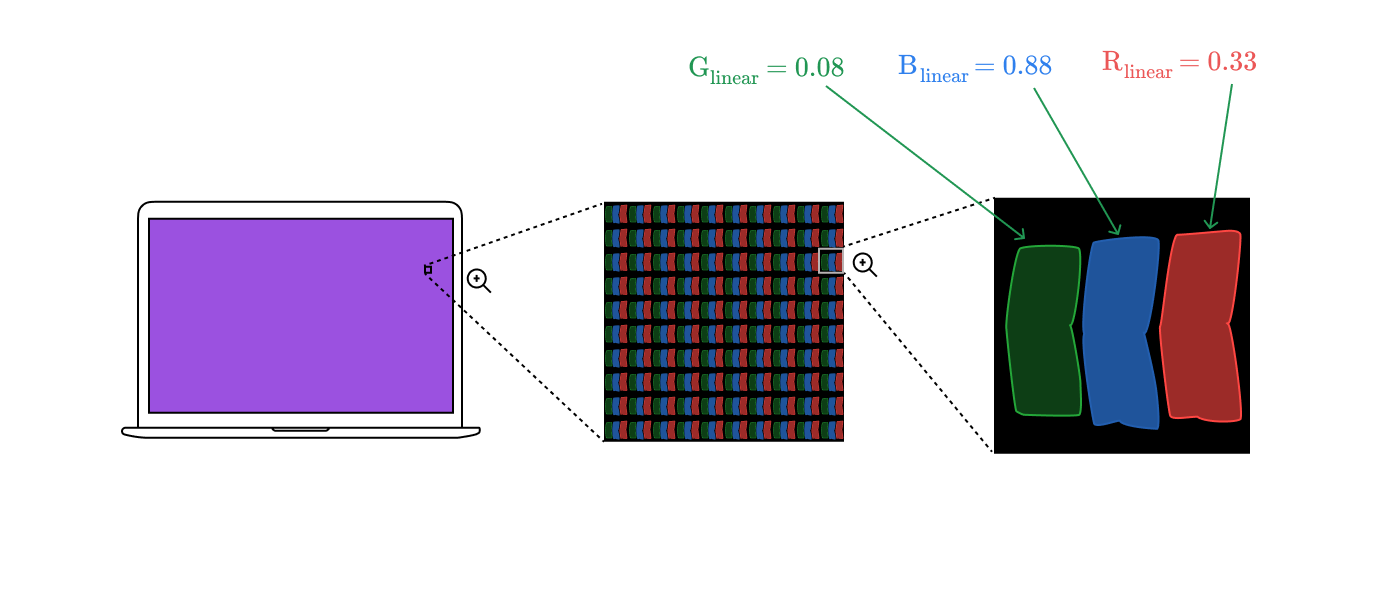
The spectral distributions of subpixels are combined into one spectral distribution for the entire pixel.

Electromagnetic radiation from a pixel passes through the cornea to the retina, exciting three types of cones.
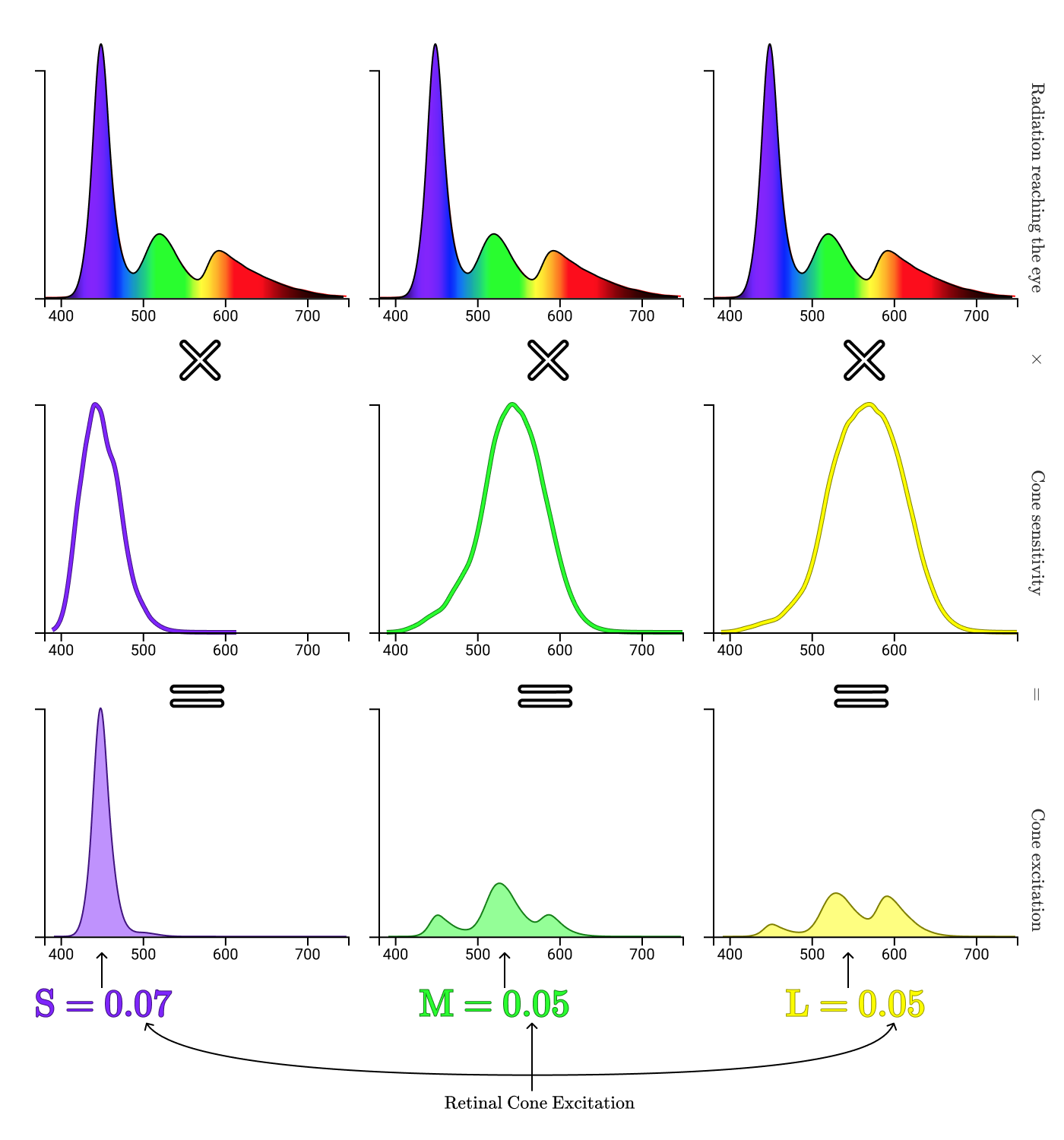
Combining all the steps together, we get an image from the beginning of the article!

Brief note on adjusting brightness

Before the sRGB values are converted to the brightness of the screen subpixels, they are attenuated according to the brightness setting of the device. Therefore, the color
0xff0000on the screen with a brightness setting of 50% may correspond to the color 0x7F0000on the same screen with a brightness of 100%. On a perfect screen, black pixels
The filter is imperfect, so when the brightness increases, black pixels will emit light when the backlight leaks through the filters. In OLED screens (as in the iPhone X and Pixel 2), the backlight is not applied, so there is a constant black regardless of the brightness of the screen.
Things I missed
In this article, we specifically omitted many aspects of color rendering and vision. For example, they did not talk about the processing of information from cones in the brain in the theory of opposite colors or the effects of color constancy . We did not talk about additive mixing and subtractive color synthesis . They did not talk about color blindness (color blindness). We did not talk about the difference between the luminous flux, luminous intensity, brightness, illumination and light radiation . We did not talk about the color profiles of ICC devices and what they are doing with color perception programs like f.lux .
I left it out of the brackets because the article turned out to be too lengthy anyway. As my friend said , even if you understand that much in life is more complicated than it seems, color will still be more complicated than you might have expected.
References
When writing this article, I spent an unusually long time simply reading the literature, because I continued to find more and more new information needed to maximize the disclosure of the topic.
Here is a short list of the most useful resources:
- Colorimetry Beginner's Guide
- CIE 1931 color space
- HSL and HSV
- Gamma correction
- Real-time rendering, third edition , pp. 210-217
I also had to process a lot of tables with data to create graphs:
- University of London Color and Vision Research Laboratory database (XYZ color matching features, cone basics)
- fluxometer.com (range of RGB subpixels on LCDs)
- CIE 15: Technical Report: Colorimetry, 3rd Edition (RGB Color Matching Features)
Special thanks to Chris Cooper and Ryan Kaplan for valuable feedback on the draft of this article.
