Search for the mysterious math on which the shape is based in iOS

This is a story about how one Figma engineer was looking for the perfect answer to a programming problem.

---

In a famous interview in 1972, Charles Eames briefly answered several fundamental questions about the nature of design . Answering the first question, he defined the design as "a layout plan for elements to achieve a specific goal."

The rest of the answers are also very concise, up to metaphors. But when Eames was asked about the role of design constraints, he stopped and gave the longest and most thoughtful answer for the entire interview: “One of the few effective keys to the design problem is the ability of the designer to recognize as many constraints as possible; his willingness and enthusiasm for working in these constraints. ”

Although I am not a designer by profession - I am a developer of FigmaWeb Design Collaborative Tool - It's easy to see that Eames’s comments apply to my work. Instead of UI elements, I compose mathematical concepts expressed in the code to create tools and functions. And the limitations of time, simplicity, support, and even aesthetics play a similar dominant role in my work.

One recent project emphasizes these parallels particularly well. I was instructed somehow to add support for the Apple figure to Figma with the fancy name of a squircle. I began to study the topic.

The study turned into a real mathematical Odyssey, full of false starts, hidden problems, emerging constraints, intelligence, tension - and resolution. In short, it was a story that, to some extent, every designer experiences almost every day.

To give pleasure to the similar mathematical prodigies of mine and to show the entire design process using mathematics, each step is described below: from the first square to the final result.

Quadrocircle: rounding operator

The story began long before I founded Figma, namely June 10, 2013 - the day iOS 7 was released. The new OS had some kind of barely noticeable update: application icons on the main screen became more juicy, more organic. Instead of a square with rounded corners, each icon turned into a quadrocircle (squircle, a combination of the words "square / rectangle" and "circle").

You ask, what's the difference? To be honest, it’s small: the usual rectangle with rounded corners is taken as the basis, but it is slightly processed by a file at the places where the curves begin. Therefore, the transition from a straight line to a curved line becomes less sharp.

If precisely formulated in the language of mathematics, then the quadrocircle has a continuous curvature of the perimeter, but the rounded square does not. This may seem trivial, but subconsciously really has a big impact: the quadrocircle does not look like a processed square; it is perceived as a separate competent entity, as a form of a smooth pebble at the bottom of the river - a single and elementary whole.


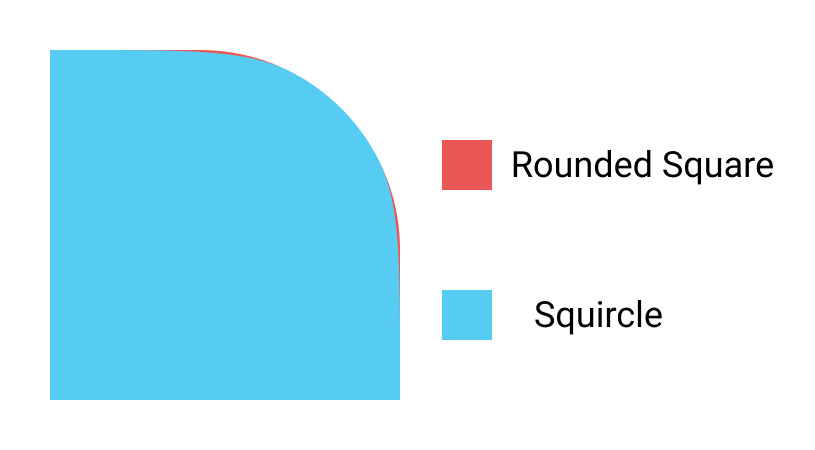
1.1. Comparison of a rounded square and a quadrocircle: obviously, the difference is small.

Industrial designers have long known how important rounding is for the perception of an object. Take a close look at the corners of your Macbook or the old-school wired headphone case under the desk lamp. Notice how difficult it is to find a position in which angles cast sharply contrasting highlights.

The reason is the continuity of curves that are specially designed by designers. It is not surprising that it was Apple, which has unique experience in developing both software and hardware, that ultimately applied the ideas of industrial design to interface design, making its icons look like physical things of its own production.

From form to formula

Of course, we at Figma love iOS designers and believe that our users should always have the right platform elements at hand. To give them access to this new form in the design, they need to find an exact mathematical description. Then we will begin to figure out how to embed this form in our tool.

Fortunately, people have been asking this question since the release of iOS 7. Of course, we are not the first to take this path! The original fundamental work of Mark Edwards contained a screenshot indicating that the shape of the icon is a special generalization of an ellipse called superellipse. The following mathematical formula describes circles, ellipses, and superellipses depending on the choice of a , b, and n :


2.1. Super-ellipse formula

Let’s say, if we choose n = 2, a = 5 and b = 3, we get a normal ellipse with large semi-axes 5 oriented along the x axis and small semi-axes 3 oriented along y . If we leave n = 2 and choose a = b = 1, then we get an ideal circle of unit radius. But if you choose n more than two, you get a superellipse - a round elliptical shape that begins to merge with the shape of the rectangle in which it is inscribed, where the corners become perfectly straight if ntends to infinity. It was originally assumed that Apple chose a form with n = 5. If you try this formula , you will see that it is really very close to the one used in iOS 7+.

If the true description really were such, then we could just apply some reasonable amount of Bezier curves - and then carefully integrate the new concept into Figma. But unfortunately, a careful follow-up analysis showed that the superellipse formula is not entirely suitable (although today true superellipses are really used as other icons). In fact, for all options nin the above equation there is a small but systematic discrepancy compared to the actual shape of the icon.

This is the first dead end in history: we have an elegant simple equation for something very similar to the iOS quadrocircle, but it is fundamentally wrong. But we must give our users the right equation.

Moving forward requires serious efforts, and again I am glad to reap a crop sown by others. One researcher Mike Swanson of Juicy Bits hypothesized that the angles of a quadrocircle are based on a sequence of Bezier curves. He used a genetic algorithm to optimize similarities with the official form of Apple. The results are consistent with the original, as proven by excellent direct comparison.Manfred Schwind, who studied the iOS code directly generating the icons. Thus, we have two different approaches that give the same structure to Bezier curves: iOS 7 quadcircles are hacked and double-checked by independent researchers, and we don’t even need to calculate anything!

File in action

Two important details remain that prevent us from cloning the form directly in Figma.

Firstly, the amazing fact is that the version of the iOS formula (at least during the study) was made with some quirks - the angles are not completely symmetrical, but on the one hand there is a tiny straight segment that obviously should not be here. We do not need it, because it complicates both the code and the tests, it is easy to remove it by simply mirroring half the angle where the bug is missing.

Secondly, when aligning the aspect ratio of a real rectangle from iOS, the shape of the icon changes dramatically from the quadcircle we need to a completely different shape. Such a twist will be unpleasant for designers, and it forces one to clearly determine what forms “should” appear under certain conditions.

The most natural and useful behavior when aligning the quadrocircle would be the gradual disappearance of the smoothing until there is no room for the transition between the round and straight parts of the corner. Further alignment should reduce the radius of the rounded section, which is consistent with Figma’s current behavior. The Apple quadrocircle formula doesn’t help us much here, because it rounds out in a fixed way: it does not give instructions on how to approach or move away from the old rounded rectangle. What we really need is a parameterizable rounding, where a certain parameter value very closely matches the shape of Apple.

As an additional bonus, if we can parameterize the transformation of a rounded rectangle into a quadrocircle, then we can quite apply the same process in other places of Figma where rounding is used: stars, polygons and even corners in arbitrary hand-drawn vector networks. Despite the complexity, it starts to look much more complete and valuable features than just adding the iOS 7 quadrocircle. Now we give designers an infinite variety of new forms for use in many situations, and one of them corresponds to the quadrocircraft icon with which it all started.

The requirement that our round-off curve is smoothly adjustable, but at the same time conform to the shape of iOS 7 at a certain convenient point from the adjustment range, is the first limitation that has arisen in our history and is difficult to satisfy. For a ballerina, a similar task would be to design a whole jump from one photograph in flight, so that at some point the jump phase corresponds to the photograph. Sounds damn hard. So maybe you still need some kind of calculation?

Powerful tool: differential geometry of plane curves

Before plunging into the parameterization of the quadrocircles, let us step back and blow dust off some formal tools that will help us analyze what is happening. First of all, you need to decide how to describe the quadrocircle. Previously, in the case of superellipses, we used the equation with x and y , where all points ( x, y ) on the plane that satisfy the conditions of the equation deduced the superellipse. This is elegant in the case of a simple equation, but real quadrocircles are a patchwork of the Bezier curves connected together, which leads to an uncontrolled pile of equations.

This complication can be dealt with using a more explicit approach: take one variable t, limit it to a finite interval and compare each value of t in this interval with a separate point on the perimeter of the quadrocircle (in fact, Bezier curves are almost always represented in this way). If we concentrate only on one of the angles, thereby limiting our analysis to a curved line with a clear beginning and end, then we can choose a mapping between t and the angle so that t = 0 corresponds to the beginning of the line, t = 1 corresponds to the end of the line, and a smooth change in t from 0 to 1 smoothly traced the rounded part of the corner. In mathematical language, we describe our angle of the curve r (t) , which is structured as


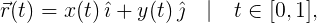
4.1. Bijection of a plane curve with [0,1]

wherex (t) and y (t) are separate functions of t for the x and y components of r. We can imagine r (t) as a peculiar story of the path of, say, your trip by car. For each point in time t between departure and arrival, you can estimate r (t) and get the position of your car on the route. From the path r (t), we can derive the velocity v (t) and the acceleration a (t) :


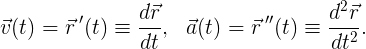
4.2. Speed ​​and acceleration of a flat curve

Finally, the mathematical curvature, which plays a major role in our history, in turn can be expressed in terms of speed and acceleration:


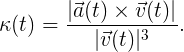
4.3. The unsigned curvature of plane curves

But what does this formula really mean? Although this may look a little complicated, the curvature has a simple geometric design, originally due to Cauchy:

1. The center of curvature C at any point P along the curve lies at the intersection of the normals to the curve P and the other normal line taken infinitely close to P . (As a note, a circle centered in C is called an osculating circle in P , from the Latin verb osculare , which means “kiss.” Isn't that wonderful?)
2. The radius of curvature R  - is the distance between C and P .
3. The curvature κ is the inverse of a R .

As shown above, the curvature κ is non-negative and does not differ by turning to the right or left. Since this difference is important to us, we form the sign curvature k from κ , assigning a positive sign if the curve turns to the right and a negative sign if to the left. This concept can also be compared to driving a car: at any point t, the sign curvature k (t) is just the angle that the steering wheel rotates at time t , with a plus sign for turning right and minus for turning left.

Geometry rules: parameterization of arc length

With the introduction of curvature, it remains to settle only a few details. First, imagine for a moment two cars moving along the corner of a quadrocircle; one car accelerates sharply, and then it brakes all the time, and the other evenly accelerates to the very end. These two different driving methods will give rise to very different track histories, even with the same path. We are only concerned about the shape of the corner, not the way to achieve it, since how can they lead to a common denominator? The main thing here when marking history points is not to use time, but the total distance traveled, that is, the length of the arc. That is, instead of the question "Where was the car in ten minutes of travel?" it’s better to answer the question “Where was the car ten miles from the start of the trip?” This way of describing the trajectory captures only the geometry and nothing more.

If we have some history of the path r (t) , we can always extract the length of the arc s as a function of the time t of the path, integrating the speed as follows:


5.1. Arc length integral

If we can invert this relation and find t (s) , then we can substitute it instead of t in our history of the path r (t) in order to obtain the desired parameterization of the arc length r (s) . The parameterization of the arc length for the path is equivalent to the history of the path of a car moving at a unit speed, therefore it is not surprising that the speed v (s) is always a unit vector and the acceleration a (s)always perpendicular to speed. Consequently, in the variant with parameterization along the arc length, the description of the curvature is simplified only up to the acceleration value.


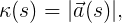
5.2. Curvature in the variant with parameterization along the length of the arc

AND, you can set the corresponding right or left sign to form the signed curvature k (s) . Obviously, most of the complications in the more general definition of curvature simply consisted of the non-geometric content of the history of the path. After all, curvature is a purely geometric quantity, so it’s very nice to see that it looks simple in geometric parameterization.

Design curvature, calculate curve

Now about another detail. We just figured out how to go from the description of the history of the path r (t) to the description of the arc length parameter r (s) and how to extract the sign curvature k (s) from it. But can we do the opposite? Design a curvature profile - and derive a parent curve from it? Let's look at the analogy with the car again: suppose that when we were driving at a constant unit speed along the entire route, we fixed the position of the steering wheel continuously throughout the entire journey. If we take this steering data and then transfer it to another driver, will he be able to completely restore the route if he correctly reproduces the positions of the steering wheel and drives at exactly the same speed? Intuitively, we have enough information to restore the parent curve, but how does this calculation look mathematically? Although a little rough, but this is possible thanks to Euler by parameterizing the length of the arc. If we choose such a coordinate system,x , then x (s) and y (s) can be restored from k (s) as follows:


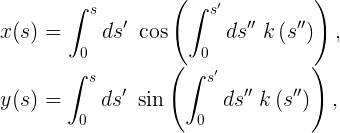
6.1. Restoring a curve from its curvature

Finally, pay attention to the argument of the sine and cosine functions: this is the integral of the sign curvature. Typically, trigonometric functions specify angles in radians as arguments. So it is in our case: the integral from a to b signed by the curvature is the rate at b minus the rate at a . Thus, if you take a rectangle and round the corner as you like, measure the curvature of the rounded part and integrate the result, as a result, we always get π / 2 .

Quadruple anatomy

Having figured out the details, we apply these analytical tools to some real forms. Let's start with the rounded corner of the rectangle, with a corner radius equal to one. First, we construct the angle itself, and then the curvature as a function of the length of the arc:


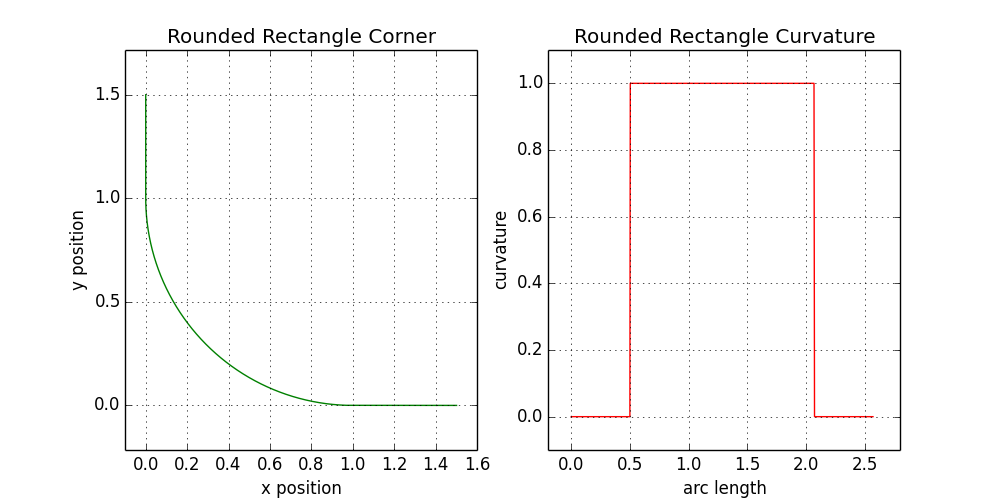
7.1. Analysis of the curvature of a rounded rectangle

Now we repeat the process for the corners of real Apple quadrocircles - and see that their curvature is very different:


7.2. Quadrocircle Curvature Analysis iOS 7

The curvature looks rather jagged, but it is not necessarily bad. As we will see later, you can find a compromise between a smooth curvature graph and a small number of Bezier curves, and there are only three of them in the iOS corner. Typically, designers are willing to sacrifice a mathematically perfect curvature profile to reduce the number of Bezier curves. Having discarded the details, the general picture appears on the right graph: the curvature rises, aligns in the middle, and then returns down.

Breakthrough: Parameterized Smoothing

Bingo! In this last observation lies the key to how to parameterize the smoothing of the angle of our quadrocircle. With zero smoothing, the curvature profile will be like a rounded rectangle: in the form of a countertop. As the smoothing gradually increases, the height of the countertop remains unchanged, but its edges turn into steep slopes, forming the profile of an isosceles trapezoid (of course, as before, with a common angle π / 2 ). When smoothing approaches the maximum, the flat part of the trapezoid disappears - and we get a wide isosceles triangle, the height of which corresponds to the height of the original countertop.


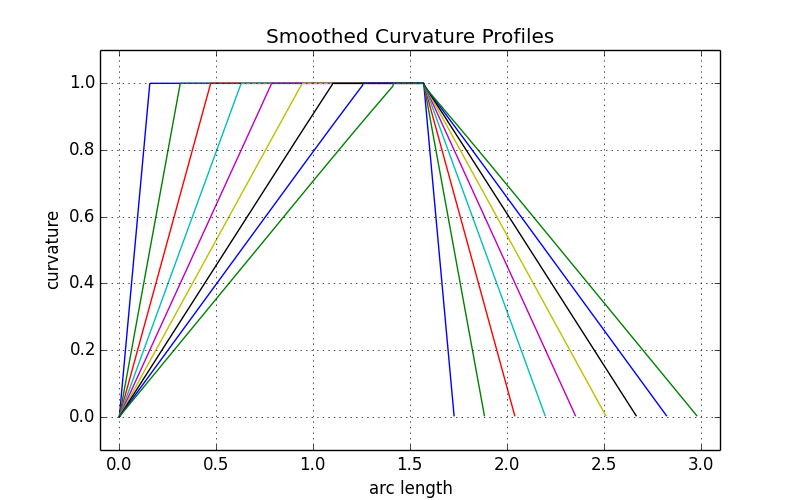
8.1. Curvature profiles for various values ​​of the smoothing parameter

Let us try to express this sketch of the curvature profile in mathematical terms using ξas a smoothing parameter that changes from zero to one. To envisage use with other shapes where there are no right angles, we also introduce a rotation angle θ , which in the case of a rectangle is π / 2 . By combining them together, a piecewise continuous function can be expressed in three parts: one for raising curvature, one for a flat top and a third for descent:


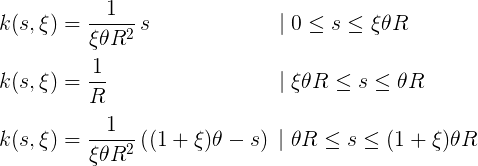
8.2. Parametrization of the curvature profile of a quadrocircle

Note that the first and third parts (ascent and descent) disappear when ξ approaches zero, and the middle part (flat top) disappears when ξ approachesto unit. Above, we showed how to go from the curvature profile to the parent curve. Let's try to do this on the first equation that describes a line whose curvature starts from zero and is steadily increasing. First we make a simple internal integral:


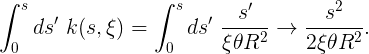
8.2. The first integral of 6.1 in relation to equations 8.2

So far, everything is fine! We can continue and form the following pair of integrals:


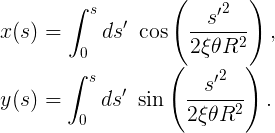
8.2. The second integral of 6.1 as applied to equations 8.2 (Fresnel integral)

Alas, here we got into a traffic jam because these integrals are not so simple. If you have heard about the connection between trigonometric functions and exponents, you can guess that these integrals are related to the error function, which cannot be expressed by elementary functions. The same applies to these integrals. So what are we going to do? The solution is beyond the scope of this article (see this post on Math StackExchange for a hint), but in this case, you can replace the sine and cosine in the power series, and then change the sum and integral:


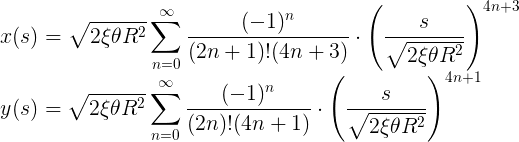
8.4. Expansion into a series of Fresnel integrals

Power series seem almost impassable, so let's take another step and explicitly write out the first few elements in each row, multiplying everything for simplification. This gives the following few elements for xand y forms:


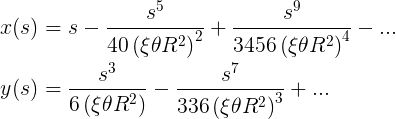
8.5. Low order elements (n <3) of 8.3

Apotheosis of clothoids

This is a concrete result! We can actually draw a graph of this pair of equations (with a reasonable choice of ξ , θ and R ) - and get the contour as a function of s . If we had an arbitrary number of elements and the ability to calculate the sums, we would see that as s increases, the curve twists into a spiral, although this happens far from the region of interest to us.

Repeating the thesis from the beginning of this article, we are again not the first to engage in such research. Due to the linear curvature, which is very useful in practice, many have come across this curve in the past. It is known as the Euler spiral, Cornu spiral or clothoid - and is widely used in the design of tracks, including roads and roller coasters.


9.1. Clotoid up to s = 5

If decomposition is used only up to n<10, as stated in 8.5, then we finally have everything we need to produce the first artifact. This series represents the ascending (first) part of equation 8.2, but it is easy to adapt it to the descending (third) part, and we will connect these parts with each other by an arc segment for a flat (second) part. This method provides a mathematically perfect angle of the quadrocircle, which exactly corresponds to the curvature design, first presented in equations 8.2. Here is the curvature analysis carried out on the clothoid for the angle of the quadrocircle with ξ  = 0.4:


9.2. The angle of the quadrocircle at ξ = 0.4 when using a ninth-order clothoid and circular arcs

Although it is nice to get such an elegant shape, it should be understood that this is only an ideal version. This exact shape will not work for several reasons. Of these, the main reason is that the center of curvature of the circular part moves as a function of the smoothing parameter ξ - ideally, it would be fixed.

More importantly, the degree of the arc length s in the conditions defined by us can reach nine. In Figma, all continuous curves must be represented by cubic Bezier curves (special cases of which are quadratic Bezier curves and lines). This limits us to the preservation of only cubic and lower order terms. That is, each of the above series for x (s) and y (s)will be truncated to one element. It is difficult to hope that after such truncation the necessary properties of the figure will be preserved.

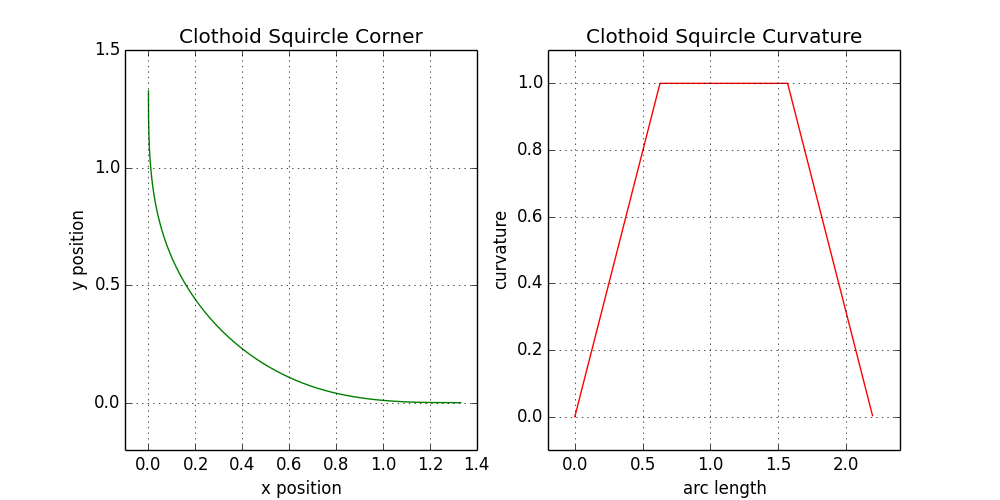
Unfortunately, it is not enough to drop members of a higher order, because the resulting construction works very poorly for large values ​​of ξ . The figure below shows the result for ξ  = 0.9:


9.3. Quadrocircle angle at ξ = 0.9 using third-order clothoid and circular arcs

This form is clearly unusable. It seems that three orders of magnitude is not enough to force the curvature to increase along the entire length of the ascent and descent. This means that we are accumulating a huge error at the time when we go out on an arc of a circle (middle segment). Unfortunately, this means that our results with clothoids are unusable. Have to start all over again.

Nothing is eternal

Let's take a step back, consider our limitations again - and try to take full advantage of our previous efforts before setting off in a new direction.

Firstly, we know that for an ideal clothoid design, the curvature profile is exactly what we need, but the center of curvature of the central circular section changes its location as a function of the smoothing parameter ξ. This is undesirable because in the UI, a point is right in the center of curvature to round a rectangle. The user sets the radius of the corner by dragging it. It will be a little strange if this point begins to move as the smoothing changes. In addition, in the form of iOS, the central section is where it would be in the case of a simple rounded rectangle, which once again indicates the complete independence of the center location from ξ . Thus, we can keep the same main goal of the design of curvature and add the restriction that the circular section maintains a fixed center of curvature when ξ changes .

Secondly, we know that designers don’t need a too complicated tool for creating corners of a quadrocircle. In the Apple shape (after removing the weird tiny straight part) there is only one Bezier curve connecting the circular section to the incoming part of the curve - maybe we can do that too?

Thirdly, we have a little incomprehensible technical limitations. They are not obvious from the very beginning, but they become a serious implementation problem. To understand them, consider a square of 100 × 100 pixels, with a standard rounding for a radius radius of 20px. This means that on each side of the square there is 60px of a straight line. If we flatten a square into a rectangle of 80 × 100px, then the straight section of the short side will be only 40px. What happens when we narrow the rectangle so much that we end up with a straight fragment? Or if we continue to narrow it further into a rectangle, say, 20 × 100px? At the moment, Figma determines the maximum applicable value for rounding corners - and uses it. Thus, in a rectangle of 20 × 100px there will be a fillet with a radius of 10px.

If p pixels are used to smooth corners with radius R and parameter ξ , then the function p (R, ξ) must be invertible in ξ (R, p).

Any smoothing process in a quadrocircle will eat even more pixels of the straight side than a simple rounding. Imagine the same square 100 × 100px, make a rounding 20px, and then apply some smoothing procedure, which removes another 12 pixels from the straight sides. This leaves us with only 36px in the straight section. What happens when the rectangle is narrowed to 60 × 100px? By analogy, it seems almost obvious that the smoothing scale should be reduced to such a level that it does not exceed the size of the straight section. But how to calculate the quantity ξ satisfying a certain number of pixels? The calculation must be fast, otherwise we will not be able to implement this function.

Again, the problem is very accurately described mathematically: if smoothing corners with radius Rand the parameter ξ consumes p pixels, then the function p (R, ξ) must be invertible in ξ (R, p) . This is a somewhat hidden limitation, which also excludes the solution of a nearby high-order clothoid.

Finally, we have a usability limitation: the change in smoothing should be at least somehow noticeable in the figure. If we pull the smoothing parameter ξ back and forth between zero and one, we would like to see the difference! Imagine that all our work leads only to subtle changes - this is unacceptable. This is fundamentally a requirement of utility, and in fact this is the most important limitation.

The simpler the better

Let's try the simplest approach that we can come up with, while meeting the above restrictions. Just take one parametrized Bezier curve, which takes the circular part and connects it to the straight side. The figure below shows the appropriate type of Bezier curve.


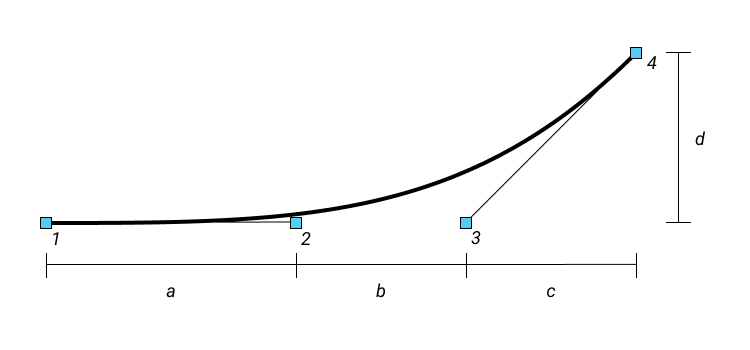
11.1. Control points of the cubic Bezier curve for the ascending part of the angle of the quadrocircle

Some properties of this Bezier curve deserve further explanation. First, control points 1, 2, and 3 line up. This ensures zero curvature at point 1, which connects to the straight part of the quadrocircle. In general, if you define a coordinate system and connect point 1 with P1 , point 2 with P2 , etc., the curvature at point 1 is given by the following formula:


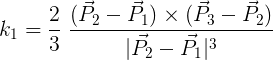
11.2. Un simplified curvature at point 1 in Fig. 11.1

The fraction reduction is clearly visible if points 1-3 are lined up. We apply the same formula to point 4, indicating the coordinates in the reverse order:


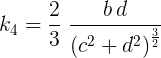
11.3. The simplified curvature at point 4 in Fig. 11.1

Ideally, the curvature will be the same as in the circular section, or 1 / R , which leads to another limitation. Finally, the values ​​of c and d are fixed due to the fact that the end of this curve must coincide with the circular part and affect the places of contact. So, the above curvature restriction just gives us a value of b :


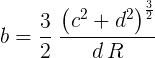
11.4. The solution for b in Fig. 11.1 providing continuity of curvature

If it is important for us to maintain the initial linear increase in curvature (which is an ideal solution with clothoids at point 1), we can set a equal to b , which fixes all the points on the Bezier curve and gives us a potential solution. Using these observations, we create a simple quadrocircle on the Bezier curves, using the smoothing ξ = 0.6.



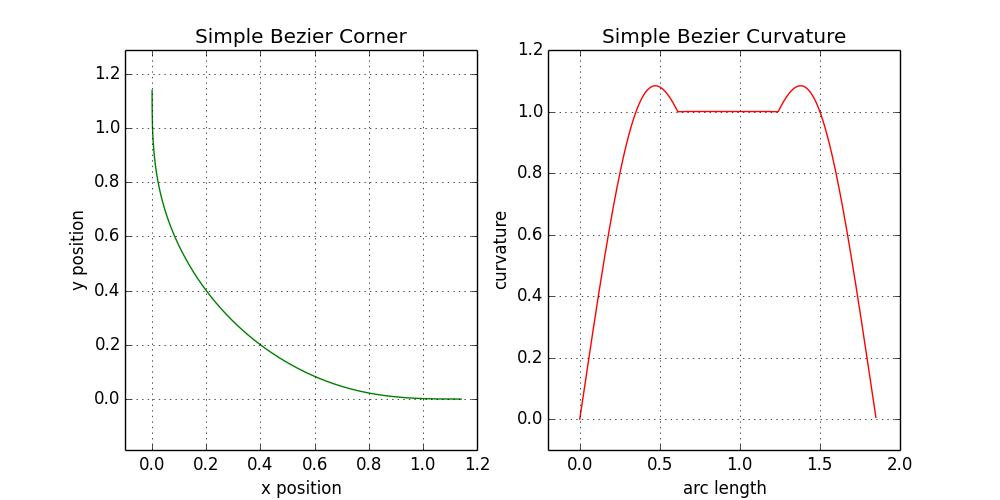
It looks good, and many clues are used here from the initial calculation of the clothoid. Unfortunately, the scatter over the entire range of ξ from 0 to 1 is practically invisible to the eye. The angles at two zoom levels are shown below, with the curves for ξ  = 0.1, 0.3, 0.5, 0.7, and 0.9 in different colors:



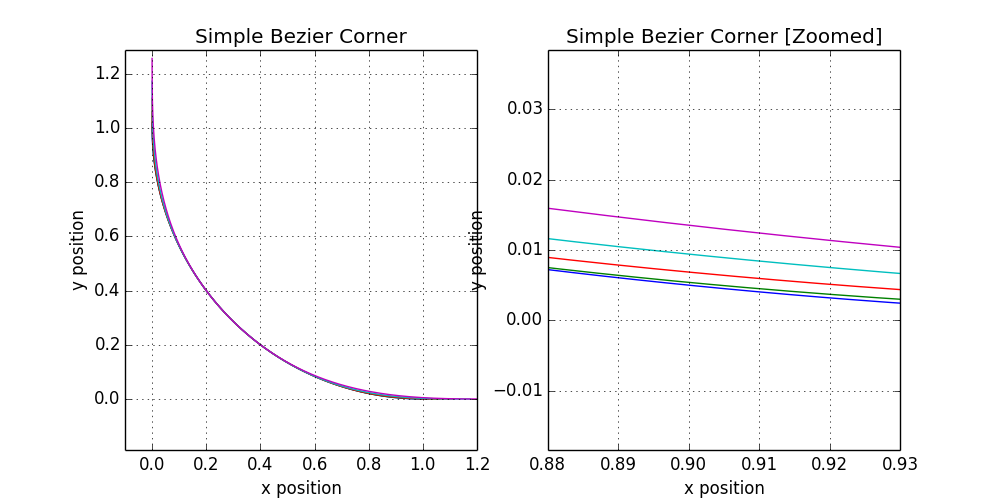
Despite the good mathematical properties, the effect is barely noticeable. Of course, this option is closer to the real product than the curve obtained earlier by reducing the number of clothoids. If only I could adjust the formula for more variation!

Small touches

You can go a step further and reflect on how to proceed. Recall that we need a reversible relationship between the pixels that are used for smoothing and the smoothing parameter ξ . First, you can focus on this transformation and make it as simple as possible. Then we’ll see what happens when we try to make quadratic circles parametrization from it.

We already know something about how pixels are used in simple rounding of corners. I do not want to mention the necessary trigonometry, but the aperture angle θ , rounded with a radius R , uses q pixels from the top of the angle, and q is defined as follows:


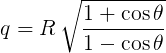
12.1. Round segment length

What if we choosep (R, ξ) based on q in the simplest way, for example:


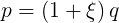
12.2. The segment length for rounding and smoothing

This means that with the maximum smoothing parameter, the same segment length will be used as we used for normal rounding. Such a choice will fix the quantity a + b in the figure above. Recall that under any circumstances c and d are firmly fixed, so the additional fixation of a + b means that we have to make one last decision: how big is a with respect to b ? Again, if you make the simplest choice, namely a = b, then we finish with the definition of the parameterization of the Bezier curve, the angles and curvatures of which are shown below:


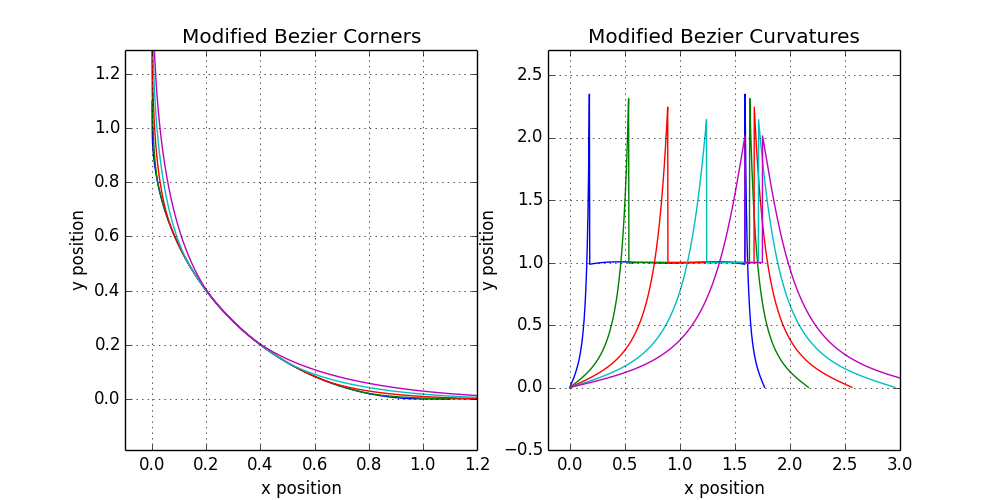
12.3. Angle shape and curvature profile for a simple smoothing scheme

This visual variety already looks promising! The curves look attractive and solid. But the curvature profile is rude. Now, if you smooth the peaks a little, then you get a serious candidate for the final release. Despite the weak profile, even in this simple family of forms there is an instance very similar to the version of the quadrocircle from Apple. It is almost good enough to roll it out with a clear conscience for our users.

Now let's move on to the profile of curvature, our last unresolved problem. Instead of evenly dividing the difference between a and b, as we did above, why not select two-thirds of the interval a, and the rest b ? This will prevent the curvature from growing too fast by shortening the long tails on the curvature profile and cutting off the peaks. Such a change leads to the following forms:


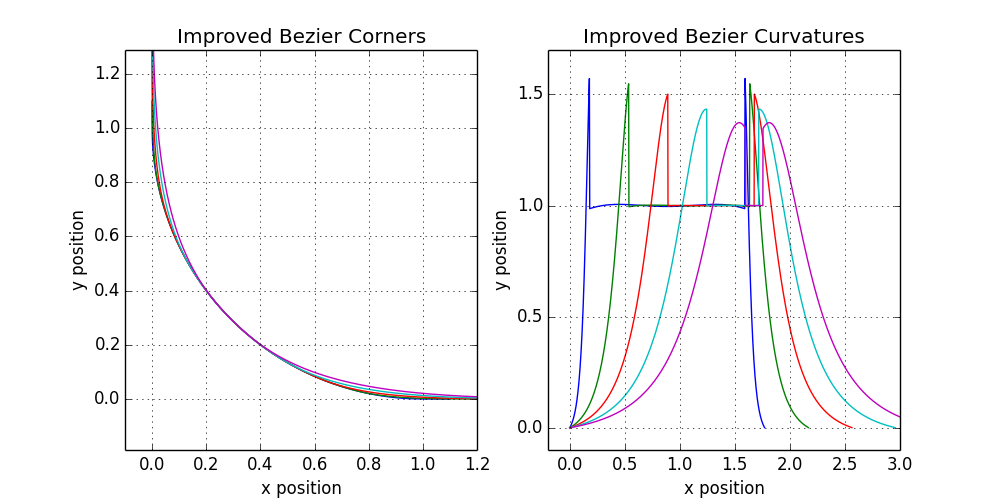
12.4. Angle shape and curvature profile for an improved simple smoothing scheme

Curvature profiles have improved significantly, and visual diversity is still sufficient to produce a real product. The smoothing parameter ξ  = 0.6 almost perfectly matches the iOS shape, and the good appearance of the curves is preserved despite the amazing simplicity of their generation. So it's time to ask a question: what prevents it from being released? Nothing.

Post-release thoughts

As a result, it is useful to reflect on the process itself. The same thing has been repeatedly confirmed in this story - the strength and effectiveness of the simplest possible approach. In the worst case, we will get a basis for comparison if it does not work. A serious assessment of it will help determine the most important thing to consider when finalizing the approach and further promotion. And in the best case, as with us, the simplest approach already gives a fairly good result!

In the end, I want to reflect on the difference between a good and a perfect product. I'm a little embarrassed that I didn't come up with a better curvature profile. I am sure that more time could be allocated, because many options remained for research. From an intellectual point of view, it’s a little unpleasant that we got such a beautiful series of clothoids, but could not use it in the final version. But there is a more important conclusion: time limits when working in a small company are very real - and a design that violates them cannot be considered good.