Distant Joining: choosing a representative set of genes
Modern methods of bioinformatics can quite accurately restore evolutionary histories based on sequences of genes or proteins of living organisms. And thanks to next-generation sequencing technologies, sequences are produced faster than they can be analyzed. That's just evolutionary reconstruction - it is computationally expensive and it would be nice to be able to get representative samples of a suitable size for analysis. How to do this and what is generally “representative” in this case - under the cut.
First of all, we will formulate clearly what is happening and what we are trying to achieve. We want to know where this gene or, say, a person came from and how it evolved. Or potatoes, or unicellular algae, the methods for any organism will be approximately the same. In biological databases, one can find related sequences of other organisms, put them into a certain magic program and get a phylogenetic tree as an output. The problem is that there are likely to be thousands of related sequences. And the construction of phylogenetic trees using maximum likelihood methods or Bayesian phylogenetics- NP-complete problem and solution consists, roughly speaking, in enumerating different trees and parameters of the evolutionary model. It usually takes me a couple of days to a week on 2 16-core AMD Opteron 6276 processors with 64 Gb of RAM for several hundred medium-length genes. There are polynomial methods of phylogenetic analysis, but they are less accurate and publishing an article based on them in a decent journal will be unrealistic.
So, you need to take the correct selection from this set: select a relatively small set of sequences of a given size and draw conclusions about the entire population from it. Next, some phylogenetic terminology will be used, explanations under the spoiler.
We define the “correct selection” as follows: let there be a certain number of treasures of interest to us in the tree that includes all the sequences from the set. What is their biological meaning, no matter; the main thing is that they are basically monophyletic (that is, they go back to a single ancestor each) and are basically separated by a more or less long branch from the rest of the tree. Each treasure corresponds to a subset of its sequences. We will consider a correct sample such that each of these subsets is represented in it by at least one sequence.
The most obvious idea is to take the sequences randomly and hope that the selection will be more or less correct. But chance - it is chance; maybe it will be correct, or maybe not. In practice, most likely it will not, because the biosphere is studied unevenly. Man and a number of model objects (Drosophila fly, baker's yeast, Escherichia coli E. colietc.) are studied in great detail and everything that is possible is repeatedly sequenced for them. Economically or medically significant objects (for example, rice and HIV) and the closest relatives of significant objects (for example, primates as relatives of a person) have been studied a little worse, but also very well. But unicellular plankton, no matter how diverse it is, is of little interest to anyone and is relatively rarely sequenced. Therefore, in a set of 100 homologous genes, 30 sequences of animals, 30 sequences of plants, 20 sequences of fungi, and one or two sequences of all other eukaryotic groups may well appear.
For a random sample, the ratio of the number of groups as a whole will be preserved. But we do not need to save it, it still reflects the number of scientists involved in a particular taxon and their financing rather than some biological reality. We need to reach as many groups as possible, including small ones.
Okay, the next idea is that since we already have taxonomic meta-information (which organism has which sequence), why not use it? Take one human gene, take more or less evenly a dozen genes of other animals, a dozen genes of fungi, and so on. Not a bad idea, people do itbut not universal. If all the genes in the original set are orthologs to each other, that is, their evolution completely coincides with the evolution of their owners, then it is best to do so. But this is far from always the case. Take a look, for example, at the picture:
This is the evolution of chitin synthases (proteins responsible for chitin synthesis) from our article last year . As you can see, the mushroom proteins (Fungal class *) do not form a single treasure; instead, they are scattered at two different ends of the tree. The same thing happens with other organisms: for example, most oomycete species have one gene from each of the four oomycete treasures. Even if we accept for simplicity that there are only two treasures, they still need to be taken into account.
The conditional “ten mushroom genes” should not be a dozen genes of one of the clades, it should be several genes from one clade and several from another. The same is true for the remaining groups.
Chitin synthases have a rather complicated evolution, and for most genes the tree will be much simpler. But the complexity of a tree cannot be estimated before it is built, and therefore a universal sampling method should be able to work with such data.
Finally, the third idea. Somewhere in the beginning, casual and quicker and less reliable methods of phylogenetic analysis were mentioned. Why not build a tree with their help, not isolate treasures in it and not take a sample of them already? Yes, the tree will not be very accurate, but most likely it will be more or less similar to the true one. You can make a selection based on such a tree, and already calculate it properly. In this form, the idea is not very practical, because “highlighting treasures” is a non-trivial task. I mentioned above that the treasure is actually as many as the nodes in the tree, and it is not known in advance which of them are of interest to the user. But you can build on this idea.
One of the most common ways to quickly get a tree is to build a distance matrix for sequences (and distance metrics for biological sequences are very different) and use it to build a tree using some kind of NJ or UPGMA . Of course, the construction of the distance matrix is quadratic in time and memory from the number of sequences, but unlike ML or Bayesian phylogenetics, it is at least polynomial.
Without even building a tree, on the basis of the distance matrix, you can get a sample that will include as many sequences as possible. Since sequences in any clade are by definition more similar to each other than other sequences, this method should cover most clades. The algorithm is quite simple: we include in the sample an arbitrary sequence, for each of the remaining we remember the distance to it. Then we include in the sample the remaining one for which this distance is maximum, for the others we remember the distance to it too. Then, from the remaining ones, we select the one with the largest minimum distance to one of the sequences in the sample, add it to the sample, and remember the distance. Repeat until the sample reaches the desired size. For its resemblance to the Neighbor Joining algorithm, we called this method Distant Joining. INin code, it looks like this:
Or a picture:
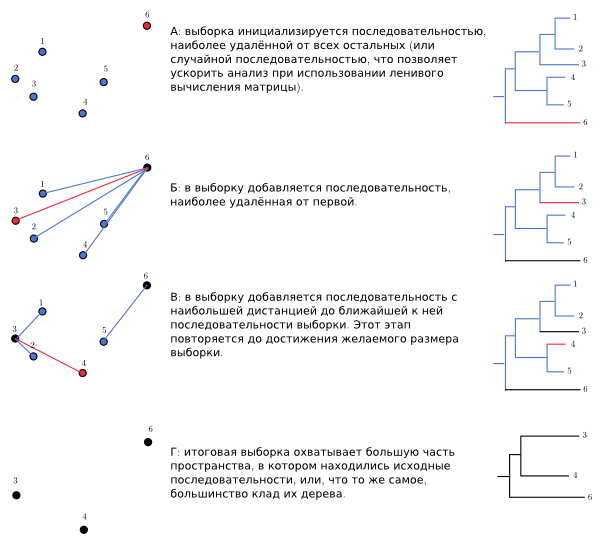
Red - added at this iteration, black - already added.
As it turned out, the described method works pretty well. Here are the results on a thousand simulated sets of sequences (blue - Distant Joining, black - RS, random selection, red - SS, choosing how many sequences are closest to the given):

For each simulation, a tree was created with a size of about a dozen or two treasures (normal distribution with an average of 15 and a standard deviation of 5) of different sizes, from units to hundreds of sequences each. According to this tree, random nucleotide sequences were generated, and then from 10% to 90% of the sequences were taken from the generated set. Efficiency was estimated as the proportion of clades represented in a reduced sample by at least one sequence. As you can see, when choosing a small number of DJ sequences, it is much more effective than the other two methods.
By the way, what kind of monstrously ineffective and obviously meaningless choice of n sequences closest to any one? This, of course, is not a method of downsampling, it is a possible artifact. Roughly speaking, a query to a biological database can be formulated either as “give me 100 sequences that are most similar to this one” or “give me all sequences that look like this at least that much”. The first formulation is useful for other tasks (and most often it is the default one), but in the case of phylogenetic analysis it can lead to serious imbalances in the data set.
Based on real data, the taxonomy-based AST method can also be included in testing.. Below are the results on two data sets: on the left is a large set of ribosomal RNAs. This is a classic marker gene, inherited with virtually no duplication or deletion, and therefore is widely used to study the evolution of species. On the right is a set of chitin synthases from the tree above.

The result is fairly predictable: in the case of rRNA, taxonomic metadata ideally describes evolution, and therefore AST greatly circumvents other methods. But he does not cope with chitin synthases for the reasons described above. The horizontal line at the top is not a frame around the chart, this DJ covers all treasures even when the data set is reduced by five times.
Strictly speaking, there is nothing specifically biological in the described algorithm. Yes, in this case, I used sequences and biological metrics of the distance between them. But in the same way, you can take samples from the collections of any objects for which there is a distance matrix and the diversity of which you need to cover the sample fairly evenly.
You just need to keep in mind that Distant Joining does not fight emissions (which it perceives as significant diversity and is one of the first in the sample) and does not preserve the ratio of cluster sizes.
Python 3 prototype available on github . If he suddenly comes in handy for someone in scientific work - please quote this article here .

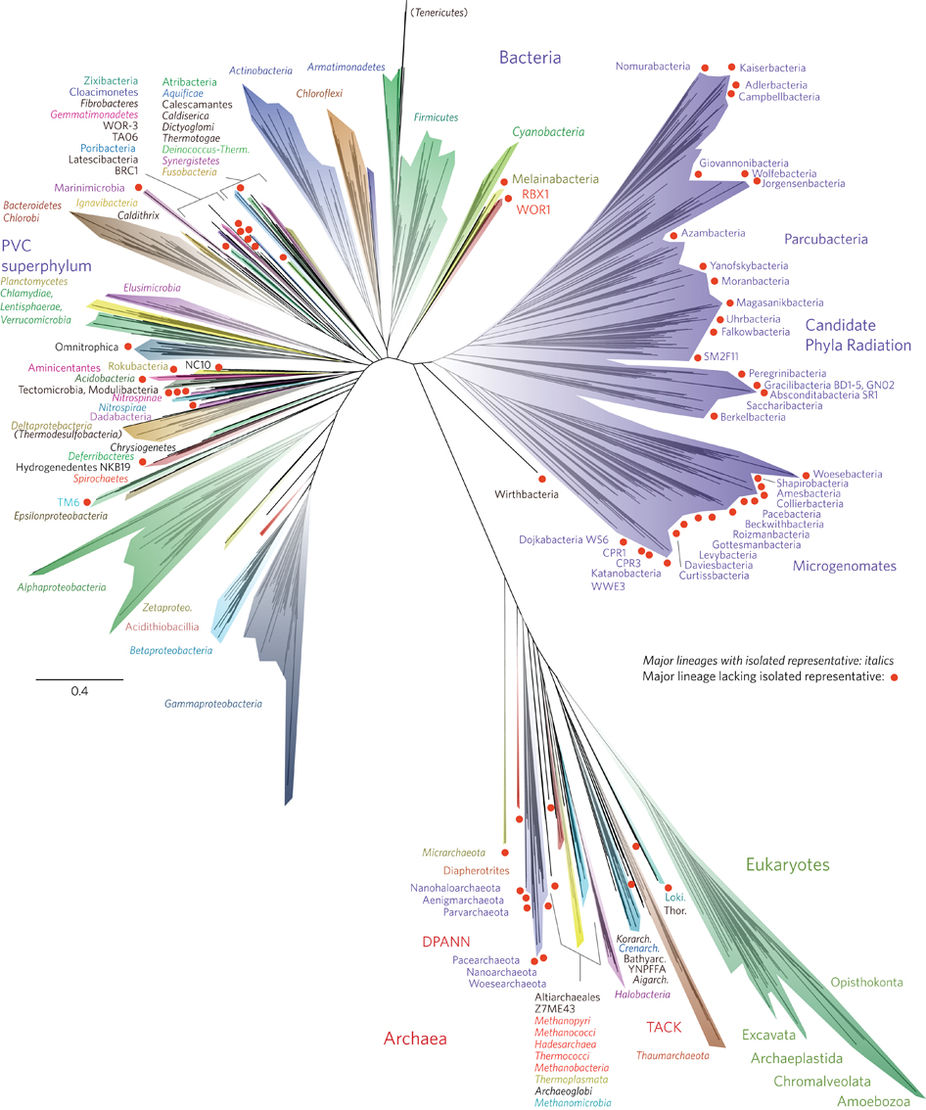
What's on KDPV?
The most complete tree of life that currently exists . All multicellular life fits in a green spot in the lower right corner and makes up a rather small fraction of it, and all animals and mushrooms (collectively called Opistokonta) - in the rightmost ledge of this spot. This is approximately the diversity of life on the planet, and such is the amount of data that is produced in the process of studying it.
Red circles, by the way, highlight groups of unicellular organisms that no one has ever seen. In no laboratory does culture grow in Petri dishes or ingenious bioreactors. Their existence became known only in recent years from metagenomic studies, when all DNA, which is, is extracted from the medium and analyzed all at once. But this is so, by the way. The picture is included in the article exclusively as the most amazing tree in recent years and is not important for understanding the article.
Red circles, by the way, highlight groups of unicellular organisms that no one has ever seen. In no laboratory does culture grow in Petri dishes or ingenious bioreactors. Their existence became known only in recent years from metagenomic studies, when all DNA, which is, is extracted from the medium and analyzed all at once. But this is so, by the way. The picture is included in the article exclusively as the most amazing tree in recent years and is not important for understanding the article.
What should be done
First of all, we will formulate clearly what is happening and what we are trying to achieve. We want to know where this gene or, say, a person came from and how it evolved. Or potatoes, or unicellular algae, the methods for any organism will be approximately the same. In biological databases, one can find related sequences of other organisms, put them into a certain magic program and get a phylogenetic tree as an output. The problem is that there are likely to be thousands of related sequences. And the construction of phylogenetic trees using maximum likelihood methods or Bayesian phylogenetics- NP-complete problem and solution consists, roughly speaking, in enumerating different trees and parameters of the evolutionary model. It usually takes me a couple of days to a week on 2 16-core AMD Opteron 6276 processors with 64 Gb of RAM for several hundred medium-length genes. There are polynomial methods of phylogenetic analysis, but they are less accurate and publishing an article based on them in a decent journal will be unrealistic.
So, you need to take the correct selection from this set: select a relatively small set of sequences of a given size and draw conclusions about the entire population from it. Next, some phylogenetic terminology will be used, explanations under the spoiler.
Key concepts and terms
To begin with, what is a phylogenetic tree? This is a binary tree that describes the appearance of many modern DNA or protein sequences from a single ancestor through successive divergences. The genes (or proteins) united by such an ancestor are homologous to each other . Even if it existed billions of years ago, there must have been a single ancestor, otherwise the whole analysis does not make sense.
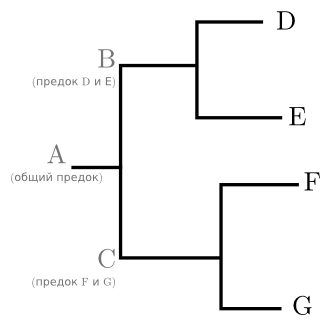
For example (figure below): once there was an ancestral gene A, which had descendants B and C. B left descendants D and E, and C - F and G. Only four sequences D, E, F and G are observed; the ancestors from A to C existed once upon a time and by now have disappeared. Accordingly, we can talk about them solely on the basis of modern sequences and mainly in terms such as “the common ancestor of such-and-such, such-and-such and such-and-such”. The part of the tree, united by a common ancestor, is called a treasure. This term can be applied both to the actual part of the graph and to sequences located at its ends. In the tree in the figure, for example, there are treasures (D, E) and (F, G). Although nominally there are as many treasures in a tree as there are internal nodes, usually a researcher is only interested in a few treasures that are significant for his work.
One may ask: why am I talking about the evolution of sequences , although everyone is used to thinking about the evolution of species. In the end, whole organisms feed, multiply and die out, rather than small pieces of DNA. This is generally true. The “tree of life" was originally invented for species, and phylogenetic trees perfectly describe their evolution. But there are two reasons for discussing trees of sequences specifically: firstly, phylogenetics as a field of bioinformatics most often deals with sequences. The evolution of organisms with a combination of characteristics is a complicated and difficult to formalize process, which, moreover, occurred millions of years ago under the influence of unknown factors and is generally not very clear with whom. The debate about what exactly was the first eukaryote, for example, is unlikely to end before the invention of the time machine. On the other hand, replacing, inserting, and deleting letters in a string is quite amenable to mathematical modeling.
Secondly, the evolution of an individual gene may differ from the evolution of the species in which it is present. The simplest scenario is described on the tree above - the common ancestor of the studied species had one copy of the studied gene, and during evolution it was simply inherited, gradually accumulating small mutations. Such genes occur to each other by orthologs . By definition, orthologs are genes of different species, dating back to the single gene of their common ancestor.
But suppose ancestor C has duplicatedthe investigated gene. There was one gene, and there were two identical ones that began to be inherited and mutate independently of each other. It is likely that one of the copies of the gene continued to do the same as before, and the second (since there is someone to perform its old function without it) will mutate and bring some new advantage. But species E or one of its recent ancestors lost this gene altogether. This happens if the gene is not so vital. Although the relationships between species have not changed, the tree will take the following form:
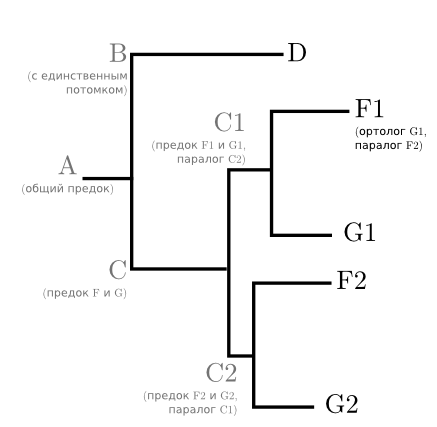
Based on this tree, it is already quite difficult to talk about the evolution of species. E is not at all, and F and G meet twice each. But it allows us to understand when the * 1 and * 2 genes appeared and how far they went. Genes of F1 and G1 fall to each other paralogs- genes of one species, going back to the only gene of his ancestor.
In addition to duplications and deletions, other events also occur: sometimes genes are acquired by organisms not from parents, but from other non-related organisms (called horizontal gene transfer or HGT), sometimes a piece from some other gene is added to one gene, or vice versa , a piece is cut off, sometimes several genes are combined into one. A lot of interesting things are happening in general. So it is not known in advance what result will be obtained if all homologous sequences are thrown into the analysis.
For example (figure below): once there was an ancestral gene A, which had descendants B and C. B left descendants D and E, and C - F and G. Only four sequences D, E, F and G are observed; the ancestors from A to C existed once upon a time and by now have disappeared. Accordingly, we can talk about them solely on the basis of modern sequences and mainly in terms such as “the common ancestor of such-and-such, such-and-such and such-and-such”. The part of the tree, united by a common ancestor, is called a treasure. This term can be applied both to the actual part of the graph and to sequences located at its ends. In the tree in the figure, for example, there are treasures (D, E) and (F, G). Although nominally there are as many treasures in a tree as there are internal nodes, usually a researcher is only interested in a few treasures that are significant for his work.

One may ask: why am I talking about the evolution of sequences , although everyone is used to thinking about the evolution of species. In the end, whole organisms feed, multiply and die out, rather than small pieces of DNA. This is generally true. The “tree of life" was originally invented for species, and phylogenetic trees perfectly describe their evolution. But there are two reasons for discussing trees of sequences specifically: firstly, phylogenetics as a field of bioinformatics most often deals with sequences. The evolution of organisms with a combination of characteristics is a complicated and difficult to formalize process, which, moreover, occurred millions of years ago under the influence of unknown factors and is generally not very clear with whom. The debate about what exactly was the first eukaryote, for example, is unlikely to end before the invention of the time machine. On the other hand, replacing, inserting, and deleting letters in a string is quite amenable to mathematical modeling.
Secondly, the evolution of an individual gene may differ from the evolution of the species in which it is present. The simplest scenario is described on the tree above - the common ancestor of the studied species had one copy of the studied gene, and during evolution it was simply inherited, gradually accumulating small mutations. Such genes occur to each other by orthologs . By definition, orthologs are genes of different species, dating back to the single gene of their common ancestor.
But suppose ancestor C has duplicatedthe investigated gene. There was one gene, and there were two identical ones that began to be inherited and mutate independently of each other. It is likely that one of the copies of the gene continued to do the same as before, and the second (since there is someone to perform its old function without it) will mutate and bring some new advantage. But species E or one of its recent ancestors lost this gene altogether. This happens if the gene is not so vital. Although the relationships between species have not changed, the tree will take the following form:

Based on this tree, it is already quite difficult to talk about the evolution of species. E is not at all, and F and G meet twice each. But it allows us to understand when the * 1 and * 2 genes appeared and how far they went. Genes of F1 and G1 fall to each other paralogs- genes of one species, going back to the only gene of his ancestor.
In addition to duplications and deletions, other events also occur: sometimes genes are acquired by organisms not from parents, but from other non-related organisms (called horizontal gene transfer or HGT), sometimes a piece from some other gene is added to one gene, or vice versa , a piece is cut off, sometimes several genes are combined into one. A lot of interesting things are happening in general. So it is not known in advance what result will be obtained if all homologous sequences are thrown into the analysis.
We define the “correct selection” as follows: let there be a certain number of treasures of interest to us in the tree that includes all the sequences from the set. What is their biological meaning, no matter; the main thing is that they are basically monophyletic (that is, they go back to a single ancestor each) and are basically separated by a more or less long branch from the rest of the tree. Each treasure corresponds to a subset of its sequences. We will consider a correct sample such that each of these subsets is represented in it by at least one sequence.
What we will not do
The most obvious idea is to take the sequences randomly and hope that the selection will be more or less correct. But chance - it is chance; maybe it will be correct, or maybe not. In practice, most likely it will not, because the biosphere is studied unevenly. Man and a number of model objects (Drosophila fly, baker's yeast, Escherichia coli E. colietc.) are studied in great detail and everything that is possible is repeatedly sequenced for them. Economically or medically significant objects (for example, rice and HIV) and the closest relatives of significant objects (for example, primates as relatives of a person) have been studied a little worse, but also very well. But unicellular plankton, no matter how diverse it is, is of little interest to anyone and is relatively rarely sequenced. Therefore, in a set of 100 homologous genes, 30 sequences of animals, 30 sequences of plants, 20 sequences of fungi, and one or two sequences of all other eukaryotic groups may well appear.
For a random sample, the ratio of the number of groups as a whole will be preserved. But we do not need to save it, it still reflects the number of scientists involved in a particular taxon and their financing rather than some biological reality. We need to reach as many groups as possible, including small ones.
Okay, the next idea is that since we already have taxonomic meta-information (which organism has which sequence), why not use it? Take one human gene, take more or less evenly a dozen genes of other animals, a dozen genes of fungi, and so on. Not a bad idea, people do itbut not universal. If all the genes in the original set are orthologs to each other, that is, their evolution completely coincides with the evolution of their owners, then it is best to do so. But this is far from always the case. Take a look, for example, at the picture:
Eukaryotic Chitin Synthase Tree

This is the evolution of chitin synthases (proteins responsible for chitin synthesis) from our article last year . As you can see, the mushroom proteins (Fungal class *) do not form a single treasure; instead, they are scattered at two different ends of the tree. The same thing happens with other organisms: for example, most oomycete species have one gene from each of the four oomycete treasures. Even if we accept for simplicity that there are only two treasures, they still need to be taken into account.
The conditional “ten mushroom genes” should not be a dozen genes of one of the clades, it should be several genes from one clade and several from another. The same is true for the remaining groups.
Chitin synthases have a rather complicated evolution, and for most genes the tree will be much simpler. But the complexity of a tree cannot be estimated before it is built, and therefore a universal sampling method should be able to work with such data.
Finally, the third idea. Somewhere in the beginning, casual and quicker and less reliable methods of phylogenetic analysis were mentioned. Why not build a tree with their help, not isolate treasures in it and not take a sample of them already? Yes, the tree will not be very accurate, but most likely it will be more or less similar to the true one. You can make a selection based on such a tree, and already calculate it properly. In this form, the idea is not very practical, because “highlighting treasures” is a non-trivial task. I mentioned above that the treasure is actually as many as the nodes in the tree, and it is not known in advance which of them are of interest to the user. But you can build on this idea.
What will we do
One of the most common ways to quickly get a tree is to build a distance matrix for sequences (and distance metrics for biological sequences are very different) and use it to build a tree using some kind of NJ or UPGMA . Of course, the construction of the distance matrix is quadratic in time and memory from the number of sequences, but unlike ML or Bayesian phylogenetics, it is at least polynomial.
Without even building a tree, on the basis of the distance matrix, you can get a sample that will include as many sequences as possible. Since sequences in any clade are by definition more similar to each other than other sequences, this method should cover most clades. The algorithm is quite simple: we include in the sample an arbitrary sequence, for each of the remaining we remember the distance to it. Then we include in the sample the remaining one for which this distance is maximum, for the others we remember the distance to it too. Then, from the remaining ones, we select the one with the largest minimum distance to one of the sequences in the sample, add it to the sample, and remember the distance. Repeat until the sample reaches the desired size. For its resemblance to the Neighbor Joining algorithm, we called this method Distant Joining. INin code, it looks like this:
leader = not_sampled[0]
reduced_list.append(leader)
minima = {x: dist(leader, x) for x in not_sampled[1:]}
while len(reduced_list) < final_count:
leader = max(minima.items(), key=lambda a: a[1])
reduced_list.append(leader[0])
del minima[leader[0]]
not_sampled.remove(leader[0])
for i in not_sampled:
d = self[(leader[0], i)]
if d < minima[i]:
minima[i] = d
Or a picture:

Red - added at this iteration, black - already added.
As it turned out, the described method works pretty well. Here are the results on a thousand simulated sets of sequences (blue - Distant Joining, black - RS, random selection, red - SS, choosing how many sequences are closest to the given):

For each simulation, a tree was created with a size of about a dozen or two treasures (normal distribution with an average of 15 and a standard deviation of 5) of different sizes, from units to hundreds of sequences each. According to this tree, random nucleotide sequences were generated, and then from 10% to 90% of the sequences were taken from the generated set. Efficiency was estimated as the proportion of clades represented in a reduced sample by at least one sequence. As you can see, when choosing a small number of DJ sequences, it is much more effective than the other two methods.
By the way, what kind of monstrously ineffective and obviously meaningless choice of n sequences closest to any one? This, of course, is not a method of downsampling, it is a possible artifact. Roughly speaking, a query to a biological database can be formulated either as “give me 100 sequences that are most similar to this one” or “give me all sequences that look like this at least that much”. The first formulation is useful for other tasks (and most often it is the default one), but in the case of phylogenetic analysis it can lead to serious imbalances in the data set.
Based on real data, the taxonomy-based AST method can also be included in testing.. Below are the results on two data sets: on the left is a large set of ribosomal RNAs. This is a classic marker gene, inherited with virtually no duplication or deletion, and therefore is widely used to study the evolution of species. On the right is a set of chitin synthases from the tree above.

The result is fairly predictable: in the case of rRNA, taxonomic metadata ideally describes evolution, and therefore AST greatly circumvents other methods. But he does not cope with chitin synthases for the reasons described above. The horizontal line at the top is not a frame around the chart, this DJ covers all treasures even when the data set is reduced by five times.
Conclusion
Strictly speaking, there is nothing specifically biological in the described algorithm. Yes, in this case, I used sequences and biological metrics of the distance between them. But in the same way, you can take samples from the collections of any objects for which there is a distance matrix and the diversity of which you need to cover the sample fairly evenly.
You just need to keep in mind that Distant Joining does not fight emissions (which it perceives as significant diversity and is one of the first in the sample) and does not preserve the ratio of cluster sizes.
Python 3 prototype available on github . If he suddenly comes in handy for someone in scientific work - please quote this article here .
