Test Method Design Methods
In the course of working with global optimization, a need arose for constructing multi-extreme test functions. Often, most of the ready-made functions, for example from Wikipedia , are not suitable for the correct evaluation of the algorithm. Some functions are single extreme; for such examples, local search algorithms are more suitable, while the other relates to ravine ones. For global optimization, it is necessary to use multiextremals, where the extrema significantly differ in magnitude.
Let us consider some methods that make it easy to construct test multiextremal functions, while allowing us to set specific properties: the Feldbaum method, functions based on hyperbolic potentials, and functions based on exponential potentials. In addition to these methods, there are harmonic multi-extreme functions and their various combinations.
This method is based on simple power one-extremal functions of the form:
The above function will have a minimum at a point , and the value at this point will be equal .
If (the degree of smoothness of the function in the region of the extremum), then at the minimum point the function will be smooth, and if , then at the minimum point the function will be angular (not differentiable).
Coefficientresponsible for the degree of coolness of the function in the extremum region.
To construct a multiextremal function, it is necessary to apply the minimum operator to the set of one-extremal functions. The general view will be as follows:
Example:
The graph of lines of equal levels of the given function will look as follows:

Slice function at :
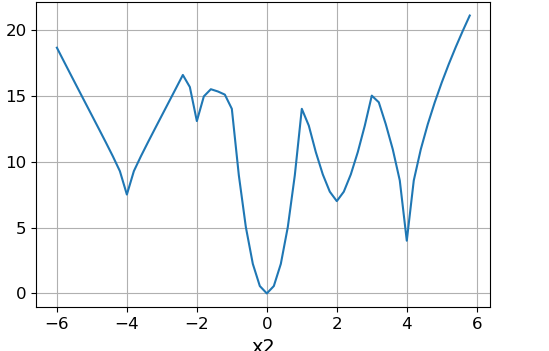
Slice function at :
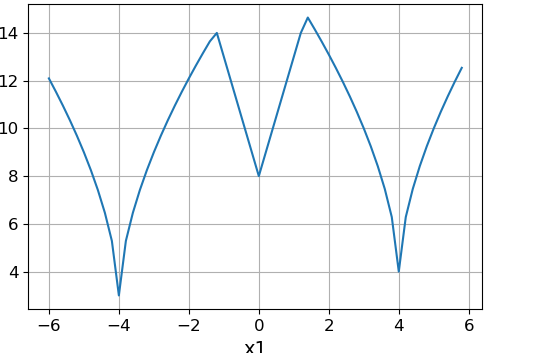
The above function has minima at the points: (0, 0), (-2, 0), (0, -2), (0, 4), (2, 2), (4, 0), (4, 4 ), (-4, 4), (-4, -4), (3, -5). Global is the minimum at the point (0, 0).
Code for generating test functions:
The one-extremum function has the form:
This function also has a minimum at a point , its depth is determined by . The degree of slope is set using the coefficient, the larger it is, the narrower the extremum region and the steeper the function.
To obtain a multi-extreme function, it is necessary to apply the summation operator:
Example:
The graph of lines of equal levels of the given function will look as follows:
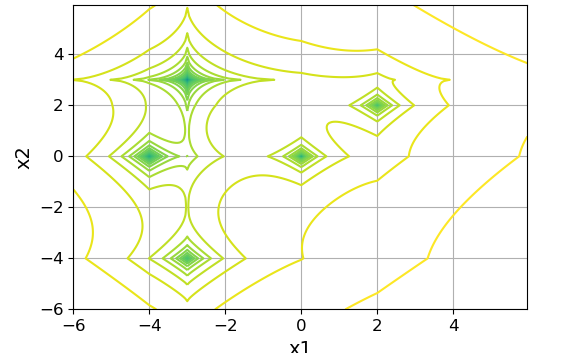
Slice function at :
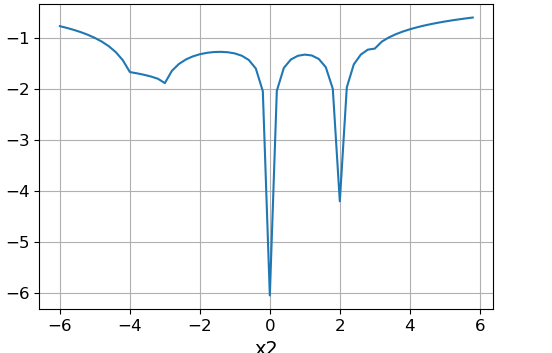
Slice function at :
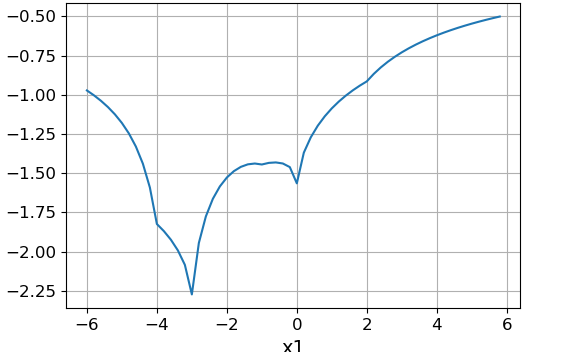
The above function has minima at the points: (-4, 0), (0, 0), (-3, 3), (2, 2), (-3, -4). Global is the minimum at the point (-3, 3).
Below the spoiler is the code for generating a test function with additive modular functions in the denominator.
The one-extremum function has the form:
Here, all letter designations have the same meaning as in the previous method.
To obtain a multi-extreme function, we also use the summation operator:
Example:
The graph of lines of equal levels is presented below:
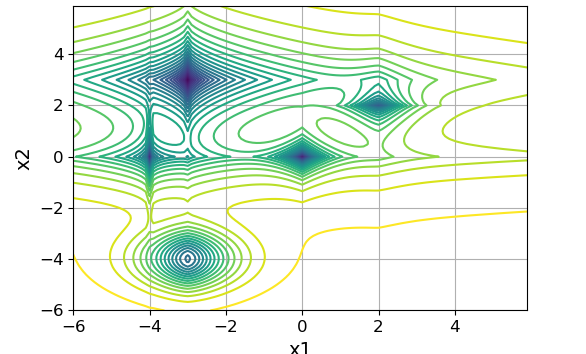
Slice function at :

Slice function at :
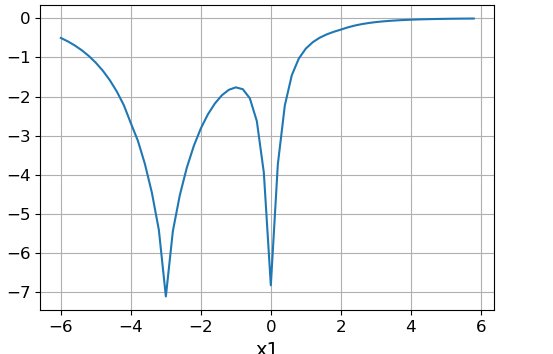
The above function has minima at the points: (-4, 0), (0, 0), (-3, 3), (2, 2), (-3, -4). Global is the minimum at the point (-3, 3).
In addition to the above methods, harmonic functions can be used, however, their construction is a more complex process. And the main disadvantage is the inability to control all local lows. You can also combine all of these methods to get even more complex functions.
Ruban A. I. Construction of multiextremal functions
Wikipedia. Test functions for optimization
Let us consider some methods that make it easy to construct test multiextremal functions, while allowing us to set specific properties: the Feldbaum method, functions based on hyperbolic potentials, and functions based on exponential potentials. In addition to these methods, there are harmonic multi-extreme functions and their various combinations.
Feldbaum Method
This method is based on simple power one-extremal functions of the form:
The above function will have a minimum at a point , and the value at this point will be equal .
If (the degree of smoothness of the function in the region of the extremum), then at the minimum point the function will be smooth, and if , then at the minimum point the function will be angular (not differentiable).
Coefficientresponsible for the degree of coolness of the function in the extremum region.
To construct a multiextremal function, it is necessary to apply the minimum operator to the set of one-extremal functions. The general view will be as follows:
Example:
Analytical view of the function
The graph of lines of equal levels of the given function will look as follows:

Slice function at :

Slice function at :

The above function has minima at the points: (0, 0), (-2, 0), (0, -2), (0, 4), (2, 2), (4, 0), (4, 4 ), (-4, 4), (-4, -4), (3, -5). Global is the minimum at the point (0, 0).
Code for generating test functions:
def get_test_function_method_min(n: int, a: List[List[float]], c: List[List[float]],
p: List[List[float]], b: List[float]):
"""
:param n: количество экстремумов
:param a: список коэффициентов крутости экстремумов, чем выше значения,
тем быстрее функция убывает/возрастает и тем уже область экстремума
:param c: список координат экстремумов
:param p: список степеней гладкости в районе экстремума
:param b: список значений функции
:return: возвращает функцию, которой необходимо передавать одномерный список
координат точки, возвращаемая функция вернет значение тестовой функции в данной точке
"""
def func(x):
l = []
for i in range(n):
res = 0
for j in range(len(x)):
res = res + a[i][j] * np.abs(x[j] - c[i][j]) ** p[i][j]
res = res + b[i]
l.append(res)
res = np.array(l)
return np.min(res)
return func
Hyperbolic Potential Functions
The one-extremum function has the form:
This function also has a minimum at a point , its depth is determined by . The degree of slope is set using the coefficient, the larger it is, the narrower the extremum region and the steeper the function.
To obtain a multi-extreme function, it is necessary to apply the summation operator:
Example:
Analytical view of the function
The graph of lines of equal levels of the given function will look as follows:

Slice function at :

Slice function at :

The above function has minima at the points: (-4, 0), (0, 0), (-3, 3), (2, 2), (-3, -4). Global is the minimum at the point (-3, 3).
Below the spoiler is the code for generating a test function with additive modular functions in the denominator.
The code
def get_tf_hyperbolic_potential_abs(n: int, a: List[float], c: List[List[float]],
p: List[List[float]], b: List[float]):
"""
:param n: количество экстремумов
:param a: коэффициенты, определяющие крутость функции в районе экстремума
:param c: список координат экстремумов
:param p: степени гладкости функции в районе экстремума
:param b: список коэффициентов, определяющих значения функции в точках экстремумов
"""
def func(x):
value = 0
for i in range(n):
res = 0
for j in range(len(x)):
res = res + np.abs(x[j] - c[i][j]) ** p[i][j]
res = a[i] * res + b[i]
res = -(1 / res)
value = value + res
return value
return func
Exponential potential functions
The one-extremum function has the form:
Here, all letter designations have the same meaning as in the previous method.
To obtain a multi-extreme function, we also use the summation operator:
Example:
Analytical view of the function
The graph of lines of equal levels is presented below:

Slice function at :

Slice function at :

The above function has minima at the points: (-4, 0), (0, 0), (-3, 3), (2, 2), (-3, -4). Global is the minimum at the point (-3, 3).
Code for generating an exponential potential function
def get_tf_exponential_potential(n: int, a: List[float], c: List[List[float]],
p: List[List[float]], b: List[float]):
"""
:param n: количество экстремумов
:param a: коэффициенты, определяющих крутость функции в районе экстремума
:param c: координаты экстремумов
:param p: степени гладкости функции в районе экстремума
:param b: значения функции в точках экстремумов
"""
def func(x):
value = 0
for i in range(n):
res = 0
for j in range(len(x)):
res = res + np.abs(x[j] - c[i][j]) ** p[i][j]
res = (-b[i]) * np.exp((-a[i]) * res)
value = value + res
return value
return func
In addition to the above methods, harmonic functions can be used, however, their construction is a more complex process. And the main disadvantage is the inability to control all local lows. You can also combine all of these methods to get even more complex functions.
List of references
Ruban A. I. Construction of multiextremal functions
Wikipedia. Test functions for optimization
