The effect of group polarization and its mathematical modeling

Introduction

Once upon a time, the American psychologist J. Stoner conducted an interesting experiment (at a time when people could be mocked with impunity so badly). He took a group of students and handed each a questionnaire with (conditionally) dichotomous questions. After they answered, Stoner invited them to discuss these issues together. And after discussion, once again answer the same questions. To his great scientific success, the result was extremely interesting.

After a group discussion, the responses began to be more “risky" in nature. The word "risky" is, of course, such a kind of euphemism, which hides the fact that people faced in a group of like-minded people with a group of ideological opponents were a little brutalized and began to more aggressively defend their initial views. This phenomenon has been called "group polarization."



By naivety, scientists then (and many now) think that discussion helps to reach consensus. Not. Discussion of a dichotomy does not help to reach consensus, if it was not planned. The discussion helps society split into two camps that cannot stand each other. And with the advent of the Internet and endless Internet disputes over any occasion, this process has become even more ambitious .

But, no matter how sad it may be, the social consequences of such a process and the endless polarizing cries of various fighters for the idea do not bother me much. But the ability to simulate this with the help of mathematics interests me.

main idea

A society is generated where each member has his own dichotomous opinion on a particularly burning issue in the form of numbers from -1 to 1. For example, wear red pants or blue. For example, a person who corresponds to the figure -0.9 - loves red pants very much, and 0.9 - blue ones. A man with zero to his pants is indifferent and wears skirts.

In addition, each person has a level of protective reactions, which prevents him from accepting new views and the desire for any reason to go personal.

Once in an iteration, some kind of social act occurs. Conditionally - "People in blue pants went to a rally." Not all, but especially ideological. At the rally, each of them interacts with random people. He may or may not agree with them, depending on how much the interlocutor is unanimous with him and is not inclined to transfer to personalities.
That's all.

After several iterations, it looks like the distribution of love for a different color of pants over the population has changed.

Model description

A “society” is modeled from $$individuals. Each individual has several characteristics:

$$- cultural affiliation. A number from -1 to 1.
$$ - level of defense reactions, “correlated” with $$. The more you fit into the culture, the stronger the defensive reaction.$$- a random variable distributed normally with respect to 0 with a standard deviation of 0.4.
$$- Ad hominem rate. The desire for any reason to go personal. Naturally, the bigger it is, the less understanding there is with a person with whom you have different views.$$- uniform distribution from 0 to 1.

Constants:
$$ - The basic step of changing the cultural context (love of the color of the pants).
$$- The basic step of changing the level of protection.

Iteration (public social act):
For random people with ideals who have$$, it is checked how big ideals are, by comparing with a random number:
If$$, then the person interacts with [1: 6] random people from the entire sample. And so for all who have inequality.
Questions may arise - why$$, but not $$. It may turn out that in the distribution there are too few people with a sufficiently large ideology, therefore$$ multiplied by 2. But in general, it can all from $$and do not depend.

Actually the interaction of people:
If people have the same views
Naturally, they cannot quarrel on the issue, therefore, for them, success and failure are not checked. But they can assert themselves by agreeing with each other. Therefore, first we find how close they are in their unanimity$$and then:

If$$ then each of them:

$$

$$

Those. they believe more in their theory and their defenses regarding their theory are strengthened.

If people of different views
Then they$$, 0.5, so that the unit does not climb. And the probability of consent is considered as follows:

$$

Here $$ - the desire to go over to the personality of the participant in the interaction in his text, $$- defensive reaction of the reader. Naturally, a complete transition to personality guarantees 0 understanding, as well as too strong defensive reactions.

If communication is successful and$$ more random $$then:

$$

$$

$$

The perceiver shifts his gaze toward the participant. Both defenses fall.

If communication is unsuccessful and$$ less random $$then:

$$

$$

The person who reads looks away from the participant and both defenses rise.
Values$$ and $$- limited by the maximum values ​​that are calculated from the original sample.

Again, questions may arise on such a calculation of the likelihood of agreement, provided that there are no protective reactions and a transition to the individual:$$. But here everything is simple$$ - a member that cannot exceed 1. “5” is a coefficient that would be good to select empirically, but in this case it is simply voluntarily appointed so that the process converges for an acceptable number of iterations.

Some modeling scenarios

Neutral society

1000 people $$. 150 iterations.


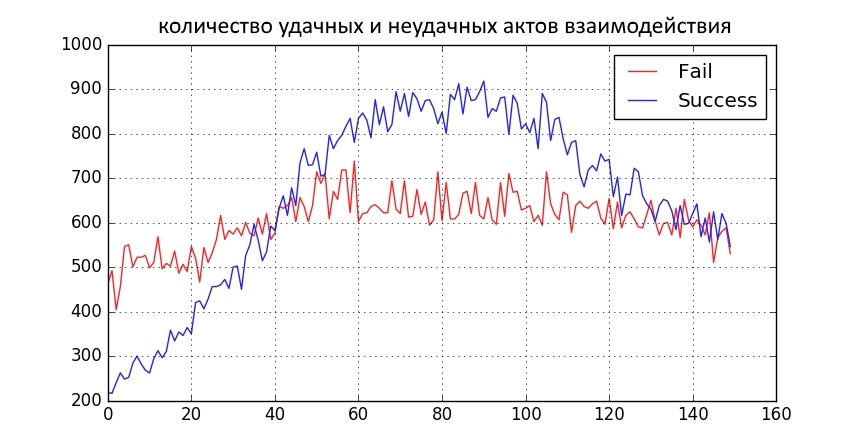
The upper two graphs show how the distribution of views over 150 iterations changed. On the x axis - the severity of views. On the y axis - the number of viewers (normalized). The bottom graph shows the number of successful and unsuccessful acts of interaction with people of opposing views for iteration.

What can be seen in the graphs?

1. Society dichotomized.
2. The red part of the distribution "pressed" to 0, but remained red. Those. There are a lot of moderate red pants lovers.
3. The “blue” part either went into a moderate minus (to the red ones), or crawled away into the “blue” radicalism.
4. The number of good interactions over the period increased, then decreased. This is predictable because the blue ones have radicalized and the red ones have remained red.
5. Due to radicalization, more people began to participate in promotions. Then the blue part of the distribution began to spread and became less involved.

Red Pants Society

1000 people $$, 150 iterations.

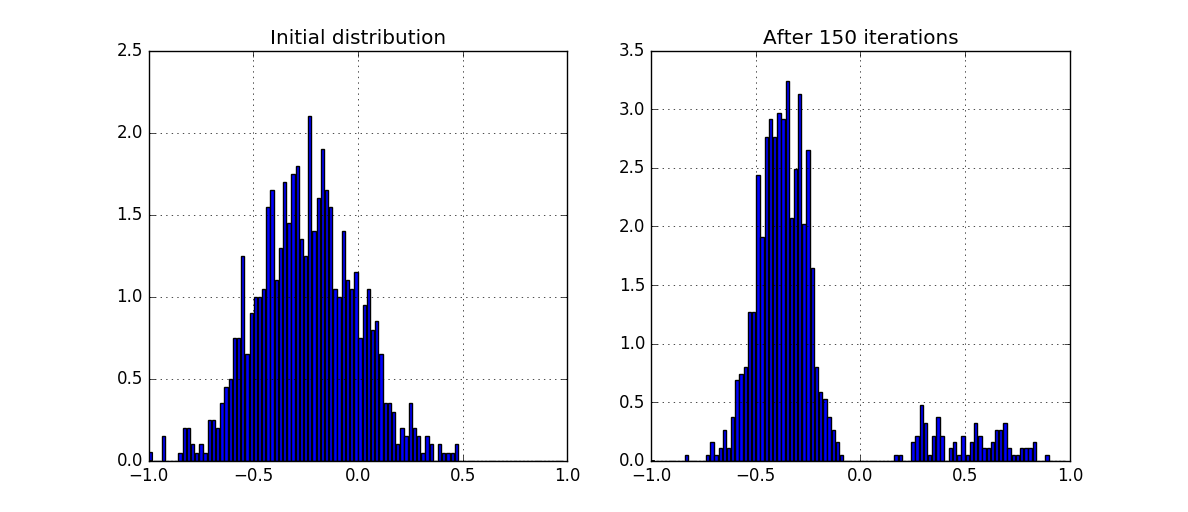
1. Society dichotomized.
2. The "red part" did NOT "collapse" to 0, although it has such a weak tendency.
3. The blue part is smeared into a roughly “uniform” distribution.
4. The number of both successful and not very communications has increased.

Dual society

500 people with $$, 500 people with $$, 150 flash mobs.




The situation is close to the first, but immediately a large level of communication failures due to the great radicalism of both groups.

Neutral homogeneous society

1000 people with c = N (0,1). 150 iterations. The homogeneity lies in the fact that the distribution is much narrower than in the first embodiment. Those. all people are very close in their initial nonsense to the color of their pants. Just a little bit do not care. Just a little bit.

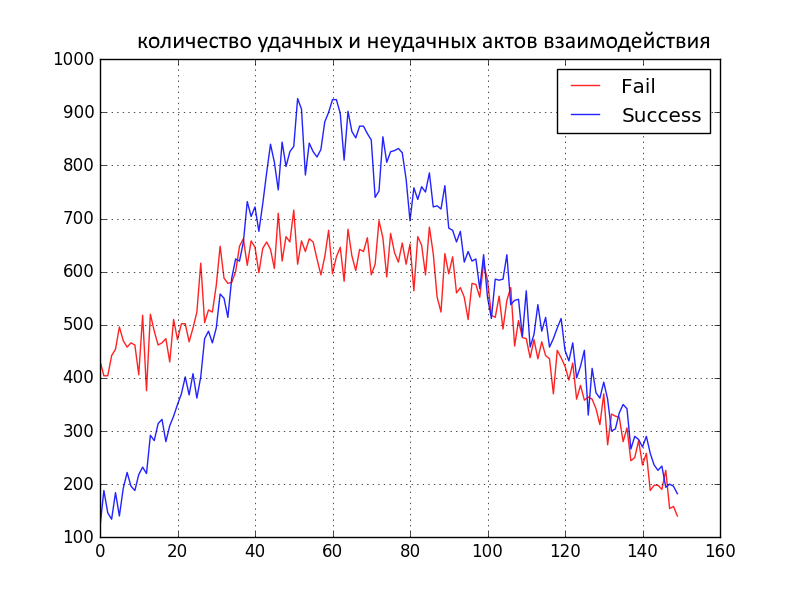
1. This is the only option when the blue pants “win” and the red ones are in the minority. This is largely due to a narrower initial distribution, due to the presence of which people are supposedly cursing less because there is less radicalism in views and defensive reactions. The population, which is smoothly indifferent to the color of the pants, is shifting towards the general adoption of blue pants.
2. Positive and negative interactions go to 0, because for the interactions of people of the same views, these parameters are not considered.

Model Limitations Considerations

• Тут не учитывается, что люди крутятся в близких им кругах, поэтому по большей части взаимодействуют со своими. НО. Это только хуже сказывается на способности слушать противоположную точку зрения, поэтому мы можем считать, что в этой модели достаточно позитивный вариант взаимодействия.
• Не учитывается, что есть всякие лидеры мнений, которые могут обращаться сразу к большой части выборки.
• Активную позицию занимает только сторона синих штанов. Только она проводит «акции». Но это как бы фича by design, а не бага.
• Коэффициенты несколько с потолка, ну а откуда их взять? Можно настроить по данным оригинального эксперимента или результатов голосования в каком-нибудь ток-шоу. Посмотрим.

Мини-вывод

Under this model, people still manage to agree on dichotomous issues. But only if they initially do not give a damn about the question. This fits well with the qualitative description of the phenomenon where “group polarization” does not arise when people are not interested or unfamiliar with the question. Moreover, it follows from the model that if people initially do not give a damn about something, it is much easier for them to accept something as their own views. The thing is how trivial, and has never been applied in practice by deeply ideological leaders of opinions. Forever they need to immediately start shouting something loudly so that people immediately split into two teams.

Article author: Alexander Bespalov, Data Analysis Specialist, Maxilect