A bit about arithmetic

Have you ever thought about how we think? How is the score low? For example, how the unit segments in the expression 1 + 1 = 2 look on the straight line . Or what is the square root of$$.

The account appeared not just to count, but to count some objects. For example, the number of apples or antelopes in the herd. That is, there is always a unit of measure.

It can be counted on fingers or sticks, that is, to set some correspondence between units. One antelope - one stick. Since any other units can be replaced with sticks, we will consider only them. The wand is an abstract unit of measure.

Simple actions

It should be noted that the score is in ascending order. Such a counting stick in itself implies the presence of the next stick. That is, the unit has a direction. So this is a unit vector.

Adding one unit vector to the end of the other, we will move along the number line, getting new values.

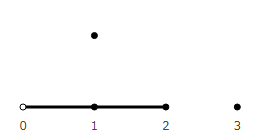
And then 4 options appear.



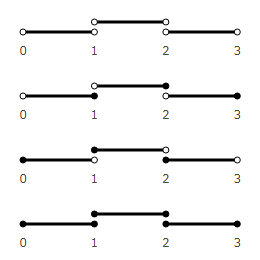
What do the ends of a single segment look like? Which option best simulates a real account?

The first does not fit. Moving in this way, we will never hit an integer. It seems that they counted to 1, but it does not belong to the first or second vector.

A fourth does not fit either. If we are at point 1, then it is not clear whether this is the first vector or the second. When we count the lambs jumping over the fence, they have no common points.

The second looks the most correct. We reached point 1 - that means they counted 1 object. Each point belongs to one vector. We will use it in the future.

The third one also looks suitable. But he has a feature - point 0 belongs to the first vector. When there is nothing yet, we believe that something already exists. This is not like a real account. But it looks like an account used in computers. The first 32-bit cell in RAM occupies bytes with addresses 0, 1, 2, 3. To make it look like a count of real objects, it would be necessary to count from the address 1 * 4 and take bytes with an offset of 0, -1, -2, -3.

So, the second option.



Please note, there is no zero. If you just take it in order, it is not entirely obvious that the reference point is not the first unit, but something before it. Perhaps that is why zero appeared later than the appearance of the account itself.

The result of addition can be represented as a single vector from the start point to the end.

How to do a subtraction? To do this, add to the consideration a vector directed in the opposite direction.



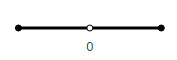
We assume that the filled point means an arrow, that is, it shows the direction of the vector.

To distinguish between these vectors, we call them positive and negative, respectively.

You can enter a change direction operation. After applying it to a positive vector, a negative one is obtained. After applying it 2 times, the original vector is obtained. In another way it can be called "unary minus" or "change of sign."

Negative vectors also form a sequence.



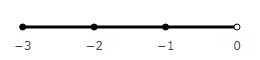
If we considered only the negative direction, we could use the same numbers as for the positive, that is, unsigned. But we are considering both, and it is necessary to distinguish the readings in the positive and negative directions. Therefore, the numbers in the negative direction have a minus sign. You can also designate positive numbers with a plus sign, but this is not necessary, the difference is so.



What does this mean? That is positive and negative 0. Geometrically they are at one point. This links the positive and negative beam of the counting direction.

Zero can be drawn filled, but for this we need to introduce a special vector of zero length, to which we add the unit ones. It can be obtained from unit vectors.

3 + -3 = 0


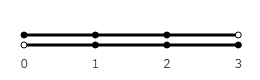
Technically, his left edge is also not turned on, but his right edge is at the same point. That is, a vector turns into a point, or in another way, a point is a special case of a vector.

An interesting point, we can go to zero on the left or on the right. Accordingly, the sign will be positive or negative. Something similar is mentioned here .

Since point 0 is a vector of zero length, we can say that, taken separately on a straight point 1, or 2, or 3, it is also a vector of zero length. It turns out that there are zero vectors that are connected non-zero. This solves the question of why a segment of nonzero length consists of an infinite number of points of zero length. Because points are always connected by nonzero vectors. These are the two opposites that make up the system. Like 0 and 1 in binary notation.

With multiplication, everything is simple - we take the whole second vector as many times as there are units in the first vector.

Division is more difficult. Just as subtraction is addition with a change of sign, so division is multiplication by the inverse number. That is, you need to specify a method for obtaining the vector 1 / N. Since it is less than a unit vector, a smaller unit of measure must be introduced.

For example, how to divide a vector of length 12 into 10 parts? We introduce a new vector of some length and set the condition that this vector repeated 10 times gives the original unit vector. As a result, we again obtain the calculations in integers. We divide 120 small vectors into 10 parts, we get 12 small or 1.2 unit ones.



How to express pi through such vectors? No way. An exact expression in units of measure means an exact decimal notation. Similarly, they cannot express the number$$= 0.333 (3) . Otherwise, it will be necessary to infinitely introduce ever smaller units of measure. You can only denote these numbers in another way - a letter or expression.
Number$$= 0.5 can be expressed, but only because the base of our number system is a multiple of this number. In the decimal system, all fractions are periodic, except for those whose denominators are a multiple of 2 or 5. This may not be entirely obvious, since we often work with finite fractions

We go beyond the borders

How to get to this point?



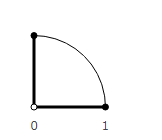
Moving only in a straight line we cannot get into it. So, we need to introduce one more unit vector perpendicular to the first. Enter a positive and negative direction, define the rules of addition and subtraction between all types of vectors. It turns out too complicated. There are many entities and set rules, besides similar to each other.

What if you approach from the other side? What needs to be done to get to a point away from the main direction? Need to turn.



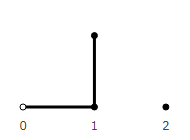
We rotate one vector and add it to another.

It is easy to see that turning a positive unit vector 2 times gives a negative vector.



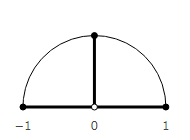
Doesn’t resemble anything? But this is a multiplication by an imaginary unit.

So what happens.$$ it is not a vector perpendicular to the material direction. $$this is a right angle rotation. This is not a unit of direction, but a unit of rotation. Multiplication of a vector by$$ means the rotation of the vector by $$through complex space. A change of sign is a turn 2 times.

“Complex space” means that if we consider a two-dimensional graph of a function$$the imaginary part $$is in a plane perpendicular to the surface of the graph. To display it, you need a third dimension, and the imaginary part$$will require the fourth. For a one-dimensional number line, the second is enough.

And what is the square root of$$? Apparently this is such a value that multiplying a unit vector by it 2 times gives a vector$$.
Times multiplying by$$ it's a turn on $$then multiplying by the root of $$ it's a turn on $$.

Check it out at Wolfram Alpha. Yeah, it is. Any expression of the form






$$ can be represented as $$where $$ this is the length of the vector, and $$ sets the rotation angle as a coefficient for $$.

$$


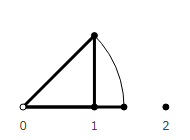
When multiplying numbers, the lengths are multiplied, and the angles are added.

$$

$$

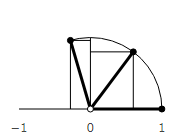
4 multiplications by i return the vector to its original state. Multiplication by$$with a degree change of 0.1 gives the usual unit circle. If you rotate it along the axis$$, we get the usual sine and cosine. What do you think sine and cosine look like in 3D? This is a spiral.

$$






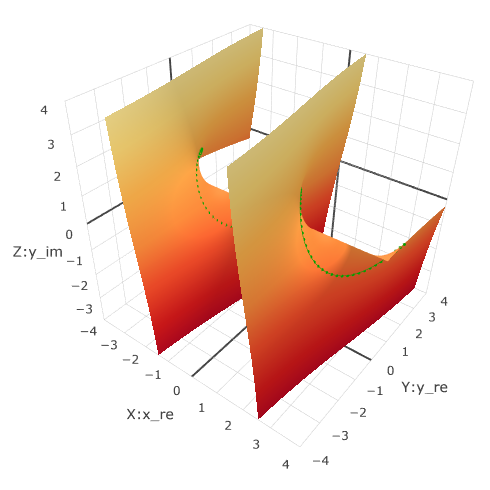
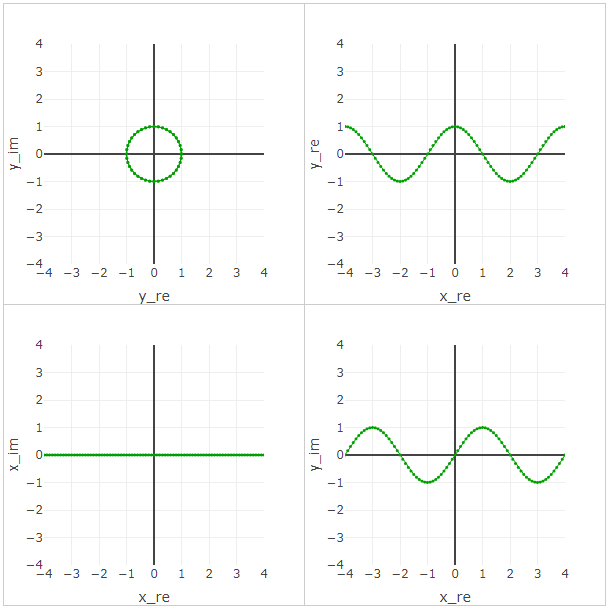
Here the period is integer, since $$revolutions are counted, not the circumference.

Pictures are clickable, the links are an interactive page with graphs. The Axis mappping block determines which 3 of the 4 axes are shown in 3D. In the field “Function 1” and “Function 2” is the javascript code from which an object of type Function is created.
The URL hash, the base64 hash, the base64 json, the json field values.
Signatures do not refer to the central axes, but to the lines along which the figures are laid.
Calculations in complex numbers are performed using math.js , graphs are made using plotly.js .

But what if you do not multiply by$$but on $$? Instead of a circle, a diverging logarithmic spiral is obtained . Let us return briefly to division. The inverse is the power of -1. This is due to movement along this logarithmic spiral. This is a function graph.







$$. The length of the vector varies from$$up to 2. The graph of the length of the radius is a regular exponential graph of the form



$$.

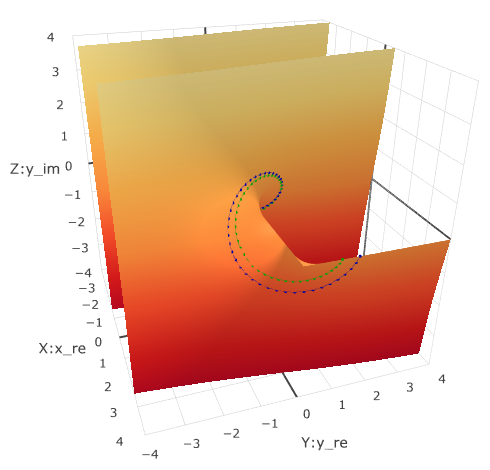
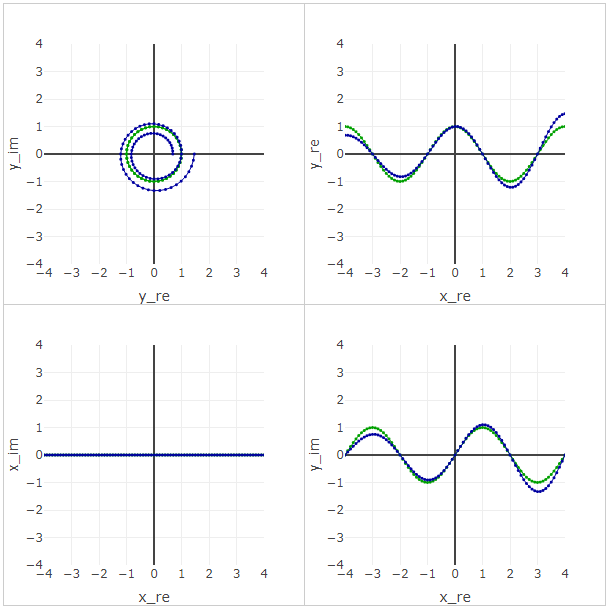
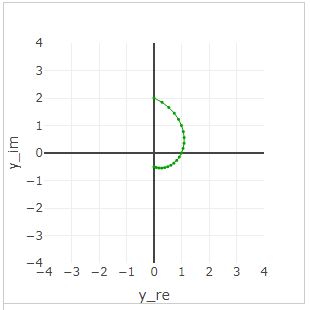
A special case

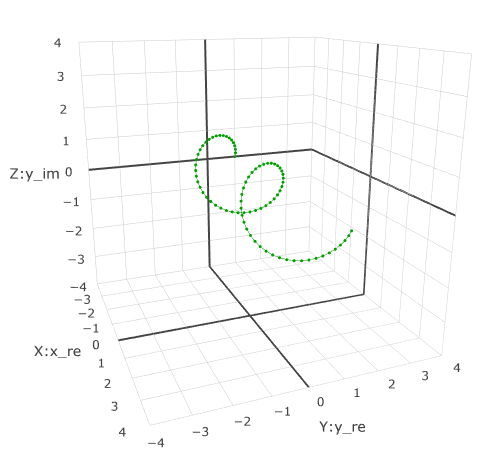
Consider the function graph $$




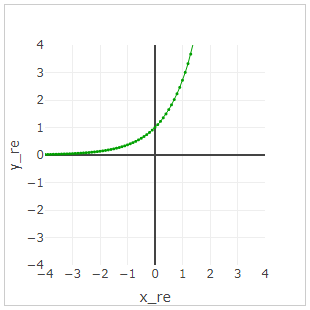
Euler's identity looks like this:
$$

This is a special case of the Euler formula. What does it mean?
It means that the value of the function$$ at the material point $$ with imaginary part $$equal to -1.

Add function graph$$. It goes perpendicular to the material and looks like



$$. therefore$$, $$, $$also equal to -1.

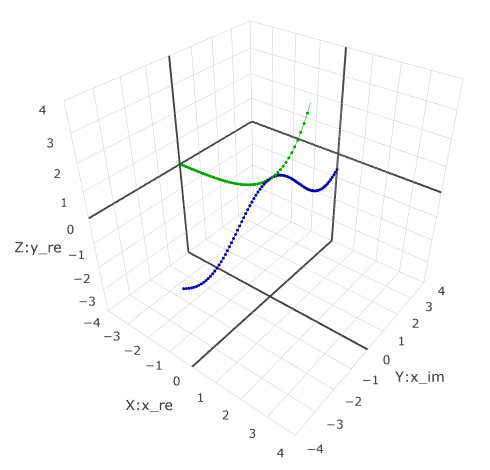
The picture that is drawn on Wikipedia can be obtained as follows . The value for the Y axis is different in Axis mapping.

In a three-dimensional form, a wavy surface is obtained. To get the latest chart, you must additionally run the function in the console . Only 2 series of points can be set in the interface, and 3 on the last one. There are functions for series management . There is also a function that shows the record of a complex number in the form






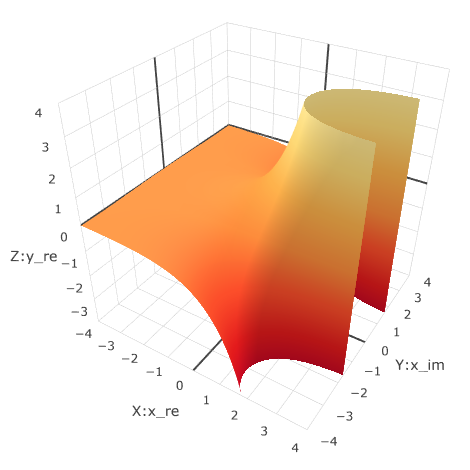
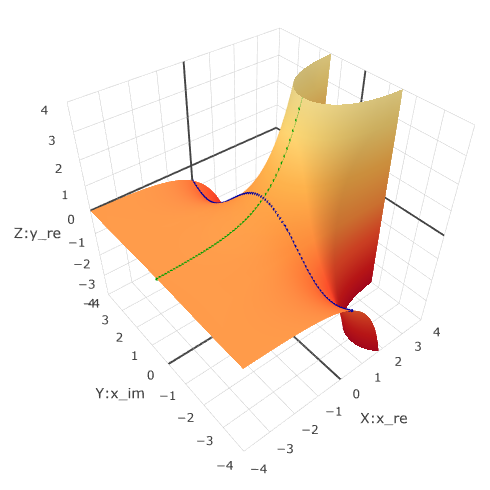
buildFuncSurface()addTraces()/deleteTraces()

altform()$$

console.log(altform(math.i.sqrt()))
0.707106781187 + 0.707106781187i = 1 * i^0.5 = 1 * i^(1/2)

There are also objects Plotlyand maththat are added by libraries.