November 27, 2017 at 16:10Binary matrix neural network
An artificial neural network in the form of a matrix, the inputs and outputs of which are sets of bits, and neurons implement the binary logic functions of several variables. Such a network differs significantly from perceptron-type networks and can give such advantages as a finite number of options for a complete enumeration of the network functions, and therefore a finite training time, and comparatively simple hardware implementation.
Attempts to create artificial neural networks are based on the fact of the existence of their natural prototypes. The method of transmitting and processing information in a natural neural network is determined by the chemical and biological properties of living neuron cells. However, the artificial neural network model does not have to completely copy both the function of neurons and the structure of the natural brain, since it implements only the function of converting information inputs to outputs. Therefore, the implementation of the function of an artificial neural network can differ significantly from its natural counterpart. An attempt to directly copy the structure of the natural brain inevitably encounters the following problems, which, if not resolved, may turn out to be insurmountable. As known,
How to find out the inputs of which neurons should be connected with the outputs of other neurons? How many neurons must be associated with each particular neuron in the network in order for the network to fulfill its function?
There are no answers to these questions yet, and connecting neurons to each other by brute force ensures an almost infinite learning time for such a network, given that the number of neurons in the real brain is in the billions.
In artificial neural networks of the perceptron type, all neurons of adjacent layers are connected to each other. And the “strength” of communication is determined by the value of the coefficients. The all-with-all connection is a solution to the problem of neuron connections using brute force. In this case, the neural network can contain only a relatively small number of neurons in the intermediate layers for an acceptable training time, for example, for several weeks [2].
Before the neural network begins to produce a result, for example, to classify images, it must go through the training stage, that is, the tuning stage. At the training stage, the interaction configuration and the general function of the network neurons are determined. In fact, to train a neural network means to choose a conversion function so that at given inputs it gives the correct outputs with a given level of error. Then, after training, we give arbitrary data to the network input, and we hope that the function of the neural network is selected accurately enough and the network will, from our point of view, correctly classify any other input data. In popular perceptron-type networks, the network structure is initially fixed, see for example [2], and the function is found by selecting the neural linkage coefficients of the intermediate layers.
The principle of decomposition of several parallel connections into a sequence of pairs or triples of bonds of only neighboring neurons is the basis of the matrix described below. The restriction is accepted that it is not at all necessary to train the network by connecting all the others to the neuron, it is enough to limit oneself to neighboring neurons only, and then sequentially reduce the error of the network learning function. This version of the neural network is based on the author’s previous work [1].
The following matrix structure of the neural network allows us to solve the problem of connecting neurons and limit the number of combinations when searching for the function of the neural network. This network also allows in theory to find the function of a neural network with zero error on training sets of inputs / outputs due to the fact that the network function is a discrete vector function of several variables.
Figure 1 shows an example of a binary matrix. The inputs and outputs of this matrix are binary four-component vectors. Inputs are fed from below, from above we get output values. Each matrix cell is a neuron with a binary function of several variables f. Each neuron has a horizontal and vertical septum, separating it from neighboring neurons and determining the flow of data. The vertical septum of a neuron, depicted to the left of each neuron, can have three positions: closed (dark bar), open to the right (green arrow to the right), open to the left (yellow arrow to the left).
The horizontal septum, depicted below the neuron, can have two positions: closed “stop” (dark bar) or open up (green arrow). Thus, the data flow in the matrix can be from bottom to top and left / right. In order to avoid the allocation of boundary discharges of data, the first and last neurons in each row are logically looped, i.e., for example, the left arrow of the first neuron in the row is the input of the last neuron in the same row, as shown in Fig. 1 for the second row neurons.
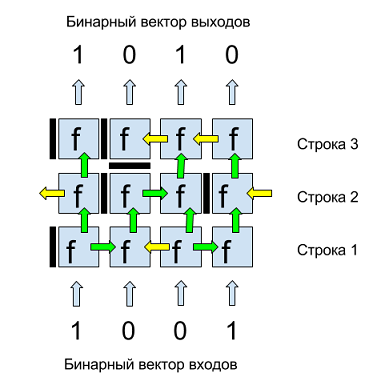
Fig. 1. An example of a binary matrix of 3 rows and 4 binary inputs / outputs.
The matrix structure is subject to the rules of step-by-step line-by-line construction. If this set of strings of neurons does not solve the problem, then the following are added to them, and so on until the objective function is achieved.
Before training, the matrix consists of one first row. Matrix training consists in sequentially adding rows. New lines are added after finding one or more septum configurations on the current line, as well as the internal parameters of neurons at which the error value on the training sets of the matrix is minimal and less than the value of the learning error on the previous line.
Neurons perform the function of converting data, transmitting or stopping a signal. The function of neuron f , depending on the current configuration of partitions and internal constants, must satisfy the following mandatory requirements:
1. be able to transmit data without changes;
2. be able to transmit a constant (0 or 1) without input data;
3. It should not depend on the sequence of application of the input data from neighboring neurons, that is, the neuron gives the resulting value from all its inputs received, as it were, simultaneously.
One of the options for such a function f is addition modulo 2 or exclusive OR or XOR, as it is often indicated in programming languages.
Transmission without change means the actual absence of a neuron and is needed only from the point of view of transmitting the matrix level without changing the data.
Depending on the position (values) of the partitions of the neuron and its neighboring neurons, each neuron can have from zero to three inputs (bottom, right and left) and always one output (up), which, however, may not be connected to the neuron of the next line , due to the position of the horizontal septum of the upper neuron “stop”.
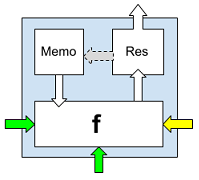
Fig. 2. A neuron with binary function f , Memo cell and Res field.
1. Data transmission without changes is provided by the option depicted in Fig. 3. Here Memo = 0, the horizontal lower partition in the “up” value, the left and right partitions in the “stop” value.
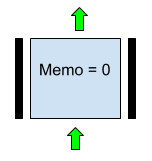
Fig. 3. A variant of the neuron parameters that implements the transfer of input from the previous line without changing in the case f = XOR.
2. The transfer of the constant is provided by the values of the horizontal and vertical “stop” partitions, and the Memo value is the value of the transmitted constant.
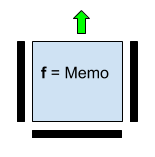
Fig. 4. A neuron with a function transferring an independent binary constant Memo. Input values below, left and right are not used.
3. The requirement of independence of the value of the neuron function from the sequence of processing the input values of the neuron is ensured by the XOR associativity.
Sequential, line-by-line construction of the matrix function allows you to effectively optimize the learning process by replacing a complete enumeration of the binary function combinations of all matrix neurons with a full enumeration of the combination of row neuron functions. One of the key points in network training is the number of combinations of a complete enumeration of the functions of neurons on one line.
For the variant of the neuron described above, the following are involved in enumerating the functions of the neuron:
1. horizontal septum with two positions: stop and up;
2. The vertical septum of the neuron with three positions: stop, left and right;
3. binary field Memo with values 0 and 1.
To calculate the number of variants of neuron functions based on combinations of these parameters, we multiply the number of variants of values for each of these parameters:
. Thus, each neuron, depending on the number of parameters that came to the input, can have one of 12 options for a binary function. We calculate the number of options for a complete enumeration of functions of one row of a matrix of 8 neurons, which, thus, can process data of 1 byte size:
.
For a modern personal computer, this is not a very large number of calculations. When choosing a neuron function with fewer options, for example, without the Memo field, the number of combinations decreases significantly to
. Even such a significantly simplified version of the neuron function demonstrates a reduction in learning errors during optimization. In software tests with different variants of neural functions in the C # language, the author was able to obtain an enumeration speed in the range of 200-600 thousand variants per second, which gives a complete enumeration of the options for the matrix row functions in about 3 seconds. However, this does not mean that, for example, an 8x8 matrix will be trained in 24 seconds. The fact is that there are several possible versions of the string function giving the same current minimum value of the learning error (metric). Which of these tens, hundreds or thousands of combinations will result in a zero error in learning the entire matrix, we do not know, and then in the worst case it will be necessary to check each of them, which leads to the construction of an optimization search tree.
The matrix learning error function will be called the metric. The metric value shows the degree of deviation of the matrix output from the expected on the training data.
An example of a metric. Assume that the inputs and outputs of the matrix are 4-bit numbers. And we want to train the matrix to multiply the input numbers by
. Let's say that three input values are used for training
, ideal for which there will be numbers 
.
, and the outputs, respectively 
, one bit per input and output string neuron, respectively.
The learning process of the matrix consists in sequentially sorting the positions of the septa of the neurons and the values of the Memo fields in the neurons of the string, which together act as search parameters. After each change of one of these parameters, that is, for example, changing the position of the horizontal septum of one of the neurons from the stop position to the up position or changing the Memo field value from 1 to 0, we get the current combination of partitions and fields and calculate the metric value .
To get the metric value on a certain combination of partitions and Memo fields, we substitute the values of the training inputs into the matrix and get the outputs.
. We translate them in decimal form
.
In this case, the learning error is 5 and the task is to find such a configuration of neurons on the current top row of the matrix for which the metric value is less
.
General algorithm for constructing a matrix optimization tree.
The details of this algorithm can be different, both in terms of saving memory and accelerating the speed of work, for example, sorting lists due to the peculiarities of the configurations of the septum of matrix neurons or discarding previous branch lists in accordance with a decrease in the current metric value.
Practical experiments show that the matrix learning algorithm in most cases converges. For example, in one of the tests with the XOR neuron function, an 8-bit-wide matrix learned to multiply by 2 numbers from 1 to 6 with zero learning error. Substituting 7 for input, I got 14 at the output, which means the matrix learned to extrapolate one move ahead, but already at number 8 the matrix gave the wrong result. All training took several minutes on a home personal computer. However, experiments with more complex training samples require different computational powers.
From plane neurons, one can go to three-dimensional ones, i.e. consider them not as square elements, but as cubes, each face of which receives or transmits data, and then (so far theoretically) you can get a completely tangible three-dimensional artificial brain.
1. AV Kazantsev, VISUAL DATA PROCESSING AND ACTION CONTROL USING BINARY NEURAL NETWORK - IEEE Eighth International Workshop (WIAMIS '07) Image Analysis for Multimedia Interactive Services, 2007.
2. Natalya Efremova, Neural Networks: practical application (habrahabr.ru)
3 . Functional completeness of Boolean functions (Wikipedia)
Prerequisites for creating a binary matrix neural network
Attempts to create artificial neural networks are based on the fact of the existence of their natural prototypes. The method of transmitting and processing information in a natural neural network is determined by the chemical and biological properties of living neuron cells. However, the artificial neural network model does not have to completely copy both the function of neurons and the structure of the natural brain, since it implements only the function of converting information inputs to outputs. Therefore, the implementation of the function of an artificial neural network can differ significantly from its natural counterpart. An attempt to directly copy the structure of the natural brain inevitably encounters the following problems, which, if not resolved, may turn out to be insurmountable. As known,
How to find out the inputs of which neurons should be connected with the outputs of other neurons? How many neurons must be associated with each particular neuron in the network in order for the network to fulfill its function?
There are no answers to these questions yet, and connecting neurons to each other by brute force ensures an almost infinite learning time for such a network, given that the number of neurons in the real brain is in the billions.
In artificial neural networks of the perceptron type, all neurons of adjacent layers are connected to each other. And the “strength” of communication is determined by the value of the coefficients. The all-with-all connection is a solution to the problem of neuron connections using brute force. In this case, the neural network can contain only a relatively small number of neurons in the intermediate layers for an acceptable training time, for example, for several weeks [2].
Before the neural network begins to produce a result, for example, to classify images, it must go through the training stage, that is, the tuning stage. At the training stage, the interaction configuration and the general function of the network neurons are determined. In fact, to train a neural network means to choose a conversion function so that at given inputs it gives the correct outputs with a given level of error. Then, after training, we give arbitrary data to the network input, and we hope that the function of the neural network is selected accurately enough and the network will, from our point of view, correctly classify any other input data. In popular perceptron-type networks, the network structure is initially fixed, see for example [2], and the function is found by selecting the neural linkage coefficients of the intermediate layers.
The principle of decomposition of several parallel connections into a sequence of pairs or triples of bonds of only neighboring neurons is the basis of the matrix described below. The restriction is accepted that it is not at all necessary to train the network by connecting all the others to the neuron, it is enough to limit oneself to neighboring neurons only, and then sequentially reduce the error of the network learning function. This version of the neural network is based on the author’s previous work [1].
The structure of the matrix and neuron
The following matrix structure of the neural network allows us to solve the problem of connecting neurons and limit the number of combinations when searching for the function of the neural network. This network also allows in theory to find the function of a neural network with zero error on training sets of inputs / outputs due to the fact that the network function is a discrete vector function of several variables.
Figure 1 shows an example of a binary matrix. The inputs and outputs of this matrix are binary four-component vectors. Inputs are fed from below, from above we get output values. Each matrix cell is a neuron with a binary function of several variables f. Each neuron has a horizontal and vertical septum, separating it from neighboring neurons and determining the flow of data. The vertical septum of a neuron, depicted to the left of each neuron, can have three positions: closed (dark bar), open to the right (green arrow to the right), open to the left (yellow arrow to the left).
The horizontal septum, depicted below the neuron, can have two positions: closed “stop” (dark bar) or open up (green arrow). Thus, the data flow in the matrix can be from bottom to top and left / right. In order to avoid the allocation of boundary discharges of data, the first and last neurons in each row are logically looped, i.e., for example, the left arrow of the first neuron in the row is the input of the last neuron in the same row, as shown in Fig. 1 for the second row neurons.
Fig. 1. An example of a binary matrix of 3 rows and 4 binary inputs / outputs.
The matrix structure is subject to the rules of step-by-step line-by-line construction. If this set of strings of neurons does not solve the problem, then the following are added to them, and so on until the objective function is achieved.
Before training, the matrix consists of one first row. Matrix training consists in sequentially adding rows. New lines are added after finding one or more septum configurations on the current line, as well as the internal parameters of neurons at which the error value on the training sets of the matrix is minimal and less than the value of the learning error on the previous line.
Neurons perform the function of converting data, transmitting or stopping a signal. The function of neuron f , depending on the current configuration of partitions and internal constants, must satisfy the following mandatory requirements:
1. be able to transmit data without changes;
2. be able to transmit a constant (0 or 1) without input data;
3. It should not depend on the sequence of application of the input data from neighboring neurons, that is, the neuron gives the resulting value from all its inputs received, as it were, simultaneously.
One of the options for such a function f is addition modulo 2 or exclusive OR or XOR, as it is often indicated in programming languages.
Transmission without change means the actual absence of a neuron and is needed only from the point of view of transmitting the matrix level without changing the data.
Depending on the position (values) of the partitions of the neuron and its neighboring neurons, each neuron can have from zero to three inputs (bottom, right and left) and always one output (up), which, however, may not be connected to the neuron of the next line , due to the position of the horizontal septum of the upper neuron “stop”.
Fig. 2. A neuron with binary function f , Memo cell and Res field.
1. Data transmission without changes is provided by the option depicted in Fig. 3. Here Memo = 0, the horizontal lower partition in the “up” value, the left and right partitions in the “stop” value.
Fig. 3. A variant of the neuron parameters that implements the transfer of input from the previous line without changing in the case f = XOR.
2. The transfer of the constant is provided by the values of the horizontal and vertical “stop” partitions, and the Memo value is the value of the transmitted constant.
Fig. 4. A neuron with a function transferring an independent binary constant Memo. Input values below, left and right are not used.
3. The requirement of independence of the value of the neuron function from the sequence of processing the input values of the neuron is ensured by the XOR associativity.
The number of combinations of full enumeration of string functions
Sequential, line-by-line construction of the matrix function allows you to effectively optimize the learning process by replacing a complete enumeration of the binary function combinations of all matrix neurons with a full enumeration of the combination of row neuron functions. One of the key points in network training is the number of combinations of a complete enumeration of the functions of neurons on one line.
For the variant of the neuron described above, the following are involved in enumerating the functions of the neuron:
1. horizontal septum with two positions: stop and up;
2. The vertical septum of the neuron with three positions: stop, left and right;
3. binary field Memo with values 0 and 1.
To calculate the number of variants of neuron functions based on combinations of these parameters, we multiply the number of variants of values for each of these parameters:
. Thus, each neuron, depending on the number of parameters that came to the input, can have one of 12 options for a binary function. We calculate the number of options for a complete enumeration of functions of one row of a matrix of 8 neurons, which, thus, can process data of 1 byte size:. For a modern personal computer, this is not a very large number of calculations. When choosing a neuron function with fewer options, for example, without the Memo field, the number of combinations decreases significantly to
. Even such a significantly simplified version of the neuron function demonstrates a reduction in learning errors during optimization. In software tests with different variants of neural functions in the C # language, the author was able to obtain an enumeration speed in the range of 200-600 thousand variants per second, which gives a complete enumeration of the options for the matrix row functions in about 3 seconds. However, this does not mean that, for example, an 8x8 matrix will be trained in 24 seconds. The fact is that there are several possible versions of the string function giving the same current minimum value of the learning error (metric). Which of these tens, hundreds or thousands of combinations will result in a zero error in learning the entire matrix, we do not know, and then in the worst case it will be necessary to check each of them, which leads to the construction of an optimization search tree.Building a tree of optimization or searching for zero matrix learning errors
The matrix learning error function will be called the metric. The metric value shows the degree of deviation of the matrix output from the expected on the training data.
An example of a metric. Assume that the inputs and outputs of the matrix are 4-bit numbers. And we want to train the matrix to multiply the input numbers by
. Let's say that three input values are used for training, ideal for which there will be numbers ., and the outputs, respectively , one bit per input and output string neuron, respectively.The learning process of the matrix consists in sequentially sorting the positions of the septa of the neurons and the values of the Memo fields in the neurons of the string, which together act as search parameters. After each change of one of these parameters, that is, for example, changing the position of the horizontal septum of one of the neurons from the stop position to the up position or changing the Memo field value from 1 to 0, we get the current combination of partitions and fields and calculate the metric value .
To get the metric value on a certain combination of partitions and Memo fields, we substitute the values of the training inputs into the matrix and get the outputs.
. We translate them in decimal form.In this case, the learning error is 5 and the task is to find such a configuration of neurons on the current top row of the matrix for which the metric value is less
.General algorithm for constructing a matrix optimization tree.
1. Задаем начальное положительное значение метрики, например max(Int32). Создаем матрицу, изначально состоящую из одной строки с начальными значениями перегородок "стоп" и нулевыми константами Memo.
2. Цикл: для каждой конфигурации перегородок и констант нейронов первой строки вычисляем значение метрики по всему обучающему набору данных.
a. Если значение метрики меньше ее текущего минимального значения, то запоминаем новое минимальное значение, а матрицу заносим в список поиска как точку ветвления, предварительно очистив этот список.
b. Если значение метрики равно текущему, то заносим текущую конфигурацию матрицы в список поиска как точку ветвления.
c. Если значение метрики больше текущего минимального, то матрица отбрасывается, берем следующую комбинацию и идем на начало цикла.
d. Если значение метрики равно нулю, то поиск закончен и найден один (из нескольких возможных) вариант обученной матрицы.
3. После перебора всех комбинаций функций на первой строке берем последовательно матрицы из списка поиска на первой строке, добавляем к ним строку и для каждой из этих матриц применяем алгоритм поиска.The details of this algorithm can be different, both in terms of saving memory and accelerating the speed of work, for example, sorting lists due to the peculiarities of the configurations of the septum of matrix neurons or discarding previous branch lists in accordance with a decrease in the current metric value.
Conclusion
Practical experiments show that the matrix learning algorithm in most cases converges. For example, in one of the tests with the XOR neuron function, an 8-bit-wide matrix learned to multiply by 2 numbers from 1 to 6 with zero learning error. Substituting 7 for input, I got 14 at the output, which means the matrix learned to extrapolate one move ahead, but already at number 8 the matrix gave the wrong result. All training took several minutes on a home personal computer. However, experiments with more complex training samples require different computational powers.
From plane neurons, one can go to three-dimensional ones, i.e. consider them not as square elements, but as cubes, each face of which receives or transmits data, and then (so far theoretically) you can get a completely tangible three-dimensional artificial brain.
References
1. AV Kazantsev, VISUAL DATA PROCESSING AND ACTION CONTROL USING BINARY NEURAL NETWORK - IEEE Eighth International Workshop (WIAMIS '07) Image Analysis for Multimedia Interactive Services, 2007.
2. Natalya Efremova, Neural Networks: practical application (habrahabr.ru)
3 . Functional completeness of Boolean functions (Wikipedia)