Neural network with amoeba solved the traveling salesman problem for 8 cities
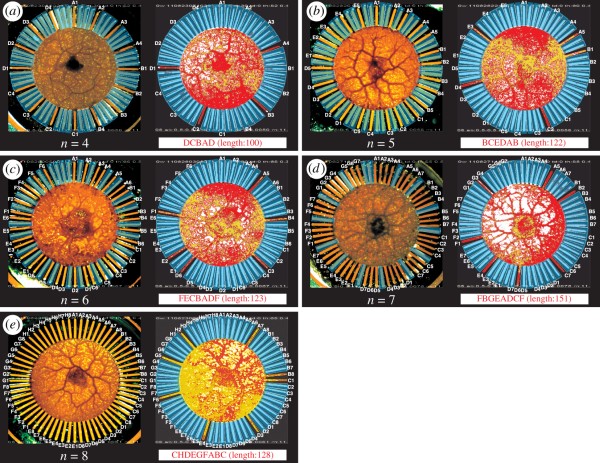
Solutions of the traveling salesman problem, obtained by amoeba-based computing system. Examples of traveling salesman tours in four, five, six, seven and eight cities, obtained in experiments where each tour is colored red on the corresponding channels from the right figure. The left panels show the transmitted bright images of the initial states (
A group of Japanese researchers from Keio University in Tokyo demonstrated that the amoeba is capable of generating approximate solutions to a surprisingly complex mathematical task known as a traveling salesman problem .
The traveling salesman task is one of the most well-known combinatorial optimization problems, which consists in finding the most profitable route that passes through the specified cities at least once and then returns to the source city.
The optimization formulation of the problem belongs to the class of NP-hard problems, however, like most of its special cases. The “decision problem” version (that is, a question that asks whether a route exists no longer than the specified value of k) belongs to the class of NP-complete problems.
The complexity of calculating the correct solution increases exponentially, the more cities are added to the task. For example, for four cities there are three possible solutions, and for six cities - 360. In the future, exponential growth continues.
Despite the great computational complexity, a large number of heuristic and exact algorithms are known that can completely solve some cases with tens of thousands of cities, and even problems with millions of cities can be approximated within 0.05% . This link is an attempt to solve for the instance from 1 904 711 cities of the Earth from the base of the National Geographic Society.
The base of the National Geographic Society of 1,904,711 cities
At the moment, the record for the minimum distance for cities on Earth is 7,515,772,107 km, it was set on March 13, 2018 using the heuristic algorithm LKH .
The classic traveling salesman problem in computer science is used as a reference test for optimization algorithms.
Amoebas are single-celled organisms that have no idea about the complexity of combinatorial optimization. They have nothing even remotely resembling the central nervous system, which makes them less suitable candidates for solving problems of such complexity. However, Japanese researchers have found that a certain type of amoeba can be used to calculate almost optimal solutions for the traveling salesman problem for eight cities.
According to a scientific article , an ameba called Physarum polycephalum , which had previously been used as a biological computer in several other experiments , participated in the experiments. This creature is considered particularly useful in biological computation, because it can expand various areas of its body in search of a more efficient way of obtaining food, and it hates the light.
To transform this natural food mechanism into a computer, Japanese researchers placed an amoeba on a special plate with 64 channels, in the direction of which the animal could pull the body. The amoeba is constantly trying to expand the body to cover as much of the nutrient plate as possible. However, each channel in the plate can be illuminated, which causes an amoeba, out of disgust at the light, to get out of this channel.
To simulate the traveling salesman problem, each of the 64 channels on the plate was assigned a city code between A and H, in addition to the number from 1 to 8, which indicates the order of the cities (the order of the cities corresponds to the order in which they visit the traveling salesman).
To program the amoeba, the researchers used a neural network that included data on the current position of the amoeba and the distance between cities to illuminate certain channels. The neural network was more likely to cover cities (channels) with greater distances between them.
In the interaction of the algorithm and amoebas, the latter takes the form that represents approximate solutions of the traveling salesman problem. The most interesting thing is that the amount of time it takes for an ameba to produce these almost optimal solutions grows linearly , although the number of solutions increases exponentially . In the near future, researchers are going to make chips with tens of thousands of channels so that the ameba can try to solve the traveling salesman problem in hundreds of cities.
The scientific article was published on December 19, 2018 in the journal Royal Society Open Science (doi: 10.1098 / rsos.180396).
