Beautiful and informative animation: cases of circular movement and vibrations
Hello.
In my previous article, I talked about how I did the animation of the planets of the solar system for my son. Thank you all for the feedback left there and the “warm” welcome. Today I prepared some more interesting animations, conditionally united under the theme “circular motion and vibrations”. In other words, what is described using cosines and sines.

For drawing I used javascript and canvas. For each example, a link is given where you can look at everything carefully. You can look at the source code, you can copy yourself - I will not mind. The material may well be useful in the classroom and electives in physics, mathematics or computer science.
So let's go.
Let's start with celestial mechanics. My favorite question for schoolchildren is: “The Earth moves [almost] in a circle around the Sun, and the Moon in a circle around the Earth. What does the moon's trajectory look like in the Sun's frame of reference? ”I hope that dear readers will be more prepared and will not begin to draw such“ curlicues ”:
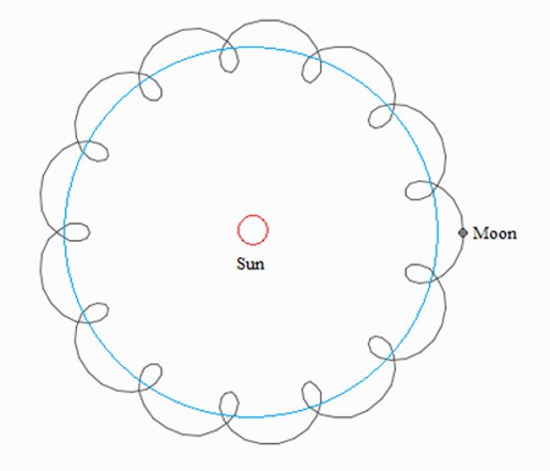
Although such a trajectory is suitable for common sense, but specifically with the Moon this does not happen. In fact, the Earth "rushes" in orbit, and the Moon, as tied, turns out to be slightly to the left, then slightly to the right. Indeed: the orbital velocity of the Earth is ~ 30 km / s, the Moon - about 1 km / s. Obviously, the speed of the moon is not enough, so that it can move in the opposite direction. A more accurate explanation is related to the calculation of forces acting on the moon (from the side of the Earth and the Sun) and on where the radius of curvature of the trajectory is directed (I will leave this for independent study).
So, the theory seems to be understandable. But still there is some understatement. I want to see how it really is. Let's make a model1 pixel scale = 30,000 km. This is a compromise option for the orbits to be distinguishable, although the scale of the image still turns out to be huge: 15,000 * 15,000 pixels. On the animation, the movement of the Earth and the Moon is described by the laws of circular motion: a blue trajectory for the Earth, and black for the Moon. Having drawn, you can see the result. It can be seen how small the total deviations of the moon's orbit from the Earth's orbit. Here, for example, a small fragment of a picture:

So, having pictures on the Internet is extremely distorted, you need to remember this.
By the way, for the sake of interest, you can make the same animation with some satellite of Jupiter. In theory, there should already be “curls”.
Once upon a time, when I was studying at the Novosibirsk Physics and Mathematics School, we had a laboratory work of Lissajs Figures, as it should be, with generators and a Soviet oscilloscope. It looked thoroughly and interesting. Depending on the frequencies of the signals applied to the inputs, different shapes are obtained on the oscilloscope screen:
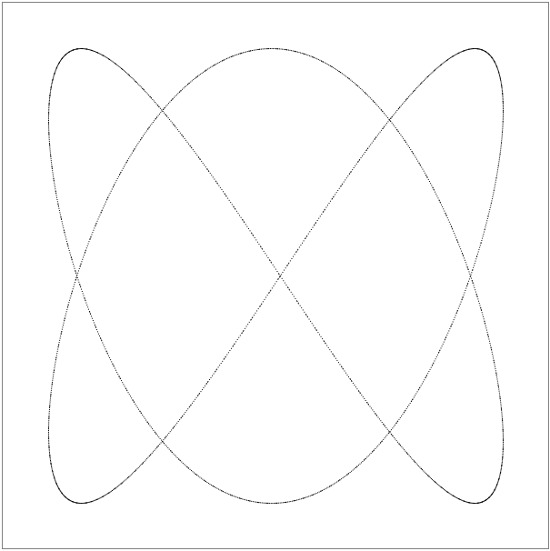
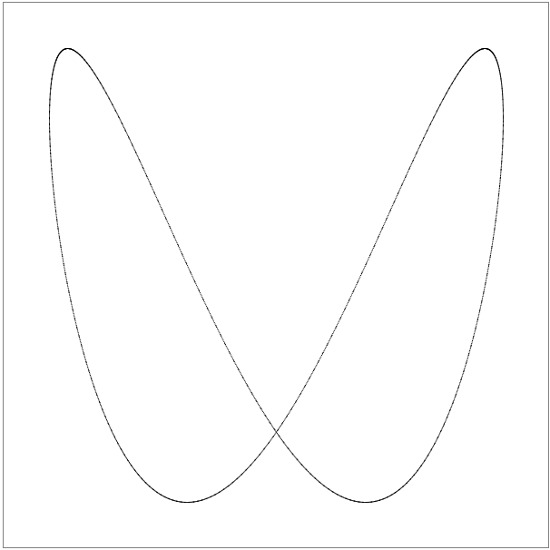
In fact, each shape is the addition of two simultaneous oscillations - along the X axis and along the Y axis. The frequencies of these oscillations can be related as 1: 1 (one X, one for Y; can be a circle, an ellipse or a straight line), 1: 2 (one for X, two for Y; a parabola or “saddle” is obtained), 1: 3, 2: 3 (more complex shapes) and so on - I think you understood the principle. You can find a detailed theoretical basis on Wikipedia , and I have prepared a separate page.where you can "play" with different coefficients.
An interesting parameter is the phase shift between oscillations. If it is continuously changed, the figure "comes to life" - begins to rotate. Here my favorite question is: “and in which direction does it rotate?” Someone says that in one direction, someone in the other, but in general you can “switch” the direction of rotation right on the go. This is purely a matter of perception. Try it and you do so.
Complicate our animation by adding a damping to it . In this case, the point gradually “falls” into the center, but, again, along an intricate and rather beautiful trajectory.

By the way, this can be done and live. As advised in one book, you need to make a cylinder with a small hole at the bottom, pour decoys into it, hang it in a doorway and swing it. Poured out semolina just and will draw a fading Lissajous figure.
A toy from childhood memories, when I, at the age of 6-7 years, drew patterns at a visit to my grandmother:

If suddenly someone, by some unheard of coincidence, is not familiar with this miracle, then running to Wikipedia . We look at the page with animation . Parameters, as in a real spirocount, are only three: the radii of the small / large circle and the distance from the point to the center of the small circle. But their different combinations give a huge number of patterns (examples you saw at the beginning of this article).
By the way, the script revealed one interesting feature: you can set such combinations in it, which are simply impossible in a real spirograph - for example, to make the inner circle more external , or in generalbring the hole out of the inner circle . The program allows you to invent anything.
Let's summarize. As you can see, our animations are at the junction of physics and computer science. It is good and interesting to read about the moon or the same Lissajous figures, but it is doubly good and interesting to see it on the screen and play with the parameters. Of course, if there are real objects to get the result, then, of course, you need to use it (for example, electronic devices - generators, an oscilloscope - to observe Lissajous figures). I am generally a supporter of "working with your hands." But often there is nothing suitable - in such cases, the animation helps out on the computer.
I would also like to specifically mention the aesthetic component. Nature, in my personal conviction, is incredibly beautiful in its essence. Agree, it's nice to look at a short and simple formula that describes a whole class of phenomena. Or, again, on the graphic representation of a formula (as with a spirograph). And, for example, magnetic field lines? And the result of a collision of particles? I remember that at the university, we also painted solutions of differential equations - even there we had our own grace and beauty. If you know all this and understand what I am talking about - let's shake hands with each other. And if you are just now interested in this - for you everything is just beginning. Today was the first step.
In my previous article, I talked about how I did the animation of the planets of the solar system for my son. Thank you all for the feedback left there and the “warm” welcome. Today I prepared some more interesting animations, conditionally united under the theme “circular motion and vibrations”. In other words, what is described using cosines and sines.

For drawing I used javascript and canvas. For each example, a link is given where you can look at everything carefully. You can look at the source code, you can copy yourself - I will not mind. The material may well be useful in the classroom and electives in physics, mathematics or computer science.
So let's go.
Moon trajectory
Let's start with celestial mechanics. My favorite question for schoolchildren is: “The Earth moves [almost] in a circle around the Sun, and the Moon in a circle around the Earth. What does the moon's trajectory look like in the Sun's frame of reference? ”I hope that dear readers will be more prepared and will not begin to draw such“ curlicues ”:

Although such a trajectory is suitable for common sense, but specifically with the Moon this does not happen. In fact, the Earth "rushes" in orbit, and the Moon, as tied, turns out to be slightly to the left, then slightly to the right. Indeed: the orbital velocity of the Earth is ~ 30 km / s, the Moon - about 1 km / s. Obviously, the speed of the moon is not enough, so that it can move in the opposite direction. A more accurate explanation is related to the calculation of forces acting on the moon (from the side of the Earth and the Sun) and on where the radius of curvature of the trajectory is directed (I will leave this for independent study).
So, the theory seems to be understandable. But still there is some understatement. I want to see how it really is. Let's make a model1 pixel scale = 30,000 km. This is a compromise option for the orbits to be distinguishable, although the scale of the image still turns out to be huge: 15,000 * 15,000 pixels. On the animation, the movement of the Earth and the Moon is described by the laws of circular motion: a blue trajectory for the Earth, and black for the Moon. Having drawn, you can see the result. It can be seen how small the total deviations of the moon's orbit from the Earth's orbit. Here, for example, a small fragment of a picture:

So, having pictures on the Internet is extremely distorted, you need to remember this.
By the way, for the sake of interest, you can make the same animation with some satellite of Jupiter. In theory, there should already be “curls”.
Figures Lissajous
Once upon a time, when I was studying at the Novosibirsk Physics and Mathematics School, we had a laboratory work of Lissajs Figures, as it should be, with generators and a Soviet oscilloscope. It looked thoroughly and interesting. Depending on the frequencies of the signals applied to the inputs, different shapes are obtained on the oscilloscope screen:


In fact, each shape is the addition of two simultaneous oscillations - along the X axis and along the Y axis. The frequencies of these oscillations can be related as 1: 1 (one X, one for Y; can be a circle, an ellipse or a straight line), 1: 2 (one for X, two for Y; a parabola or “saddle” is obtained), 1: 3, 2: 3 (more complex shapes) and so on - I think you understood the principle. You can find a detailed theoretical basis on Wikipedia , and I have prepared a separate page.where you can "play" with different coefficients.
An interesting parameter is the phase shift between oscillations. If it is continuously changed, the figure "comes to life" - begins to rotate. Here my favorite question is: “and in which direction does it rotate?” Someone says that in one direction, someone in the other, but in general you can “switch” the direction of rotation right on the go. This is purely a matter of perception. Try it and you do so.
Complicate our animation by adding a damping to it . In this case, the point gradually “falls” into the center, but, again, along an intricate and rather beautiful trajectory.

By the way, this can be done and live. As advised in one book, you need to make a cylinder with a small hole at the bottom, pour decoys into it, hang it in a doorway and swing it. Poured out semolina just and will draw a fading Lissajous figure.
Spirograph
A toy from childhood memories, when I, at the age of 6-7 years, drew patterns at a visit to my grandmother:

If suddenly someone, by some unheard of coincidence, is not familiar with this miracle, then running to Wikipedia . We look at the page with animation . Parameters, as in a real spirocount, are only three: the radii of the small / large circle and the distance from the point to the center of the small circle. But their different combinations give a huge number of patterns (examples you saw at the beginning of this article).
By the way, the script revealed one interesting feature: you can set such combinations in it, which are simply impossible in a real spirograph - for example, to make the inner circle more external , or in generalbring the hole out of the inner circle . The program allows you to invent anything.
results
Let's summarize. As you can see, our animations are at the junction of physics and computer science. It is good and interesting to read about the moon or the same Lissajous figures, but it is doubly good and interesting to see it on the screen and play with the parameters. Of course, if there are real objects to get the result, then, of course, you need to use it (for example, electronic devices - generators, an oscilloscope - to observe Lissajous figures). I am generally a supporter of "working with your hands." But often there is nothing suitable - in such cases, the animation helps out on the computer.
I would also like to specifically mention the aesthetic component. Nature, in my personal conviction, is incredibly beautiful in its essence. Agree, it's nice to look at a short and simple formula that describes a whole class of phenomena. Or, again, on the graphic representation of a formula (as with a spirograph). And, for example, magnetic field lines? And the result of a collision of particles? I remember that at the university, we also painted solutions of differential equations - even there we had our own grace and beauty. If you know all this and understand what I am talking about - let's shake hands with each other. And if you are just now interested in this - for you everything is just beginning. Today was the first step.
