The theory of happiness. Dizzy flight of a sandwich with butter
I continue to acquaint Habr's readers with chapters from his book “The Theory of Happiness” with the subtitle “Mathematical foundations of the laws of meanness”. This is not yet a popular science book published, very informally telling how mathematics allows us to look at the world and life of people with a new degree of awareness. It is for those who are interested in science and for those who are interested in life. And since our life is complex and, by and large, unpredictable, the emphasis in the book is mainly on probability theory and mathematical statistics. Here theorems are not proved and the fundamentals of science are not given; this is by no means a textbook, but what is called recreational science. But it is this almost playful approach that allows us to develop intuition, brighten up with vivid examples lectures for students and, finally, explain to nemathematicians and our children,

In this chapter, we look at the law of the sandwich and organize the whole study using the Monte Carlo method, and the analysis of dimensions. And finally, we will debunk the popular myth that it is oil that is the cause of this law of meanness.
The theme of falling sandwiches does not rest either the general public or the researchers. For decades, experiments have been carried out, films are shot, articles are written, a falling sandwich acquires legends and wrong conclusions. Not only is this useless task attracted so much attention, and if you think that all this is self-indulgence, then keep in mind that even bonuses are given for its solution, but not serious ones either. In 1995, Robert Matthews received the Snobel Prize for his "Falling Sandwich, Murphy's Law and Fundamental Constants", published in the European Journal of Physics. Despite the comic topic and the corresponding reaction of the scientific community, this is a completely interesting article, which thoroughly analyzes the process of slipping, and makes a far-reaching conclusion: on whatever planet anthropomorphic creatures live in the atmosphere, they will be doomed to the law of the sandwich. After such a triumph of useless research, one could close the topic, but why miss the opportunity to consider interesting and objectively useful methods using the example of an amusing puzzle!
We seldom throw sandwiches like a coin, at least when we are older than two years. More often than not, we involuntarily repeat approximately the same experiment: a sandwich, originally placed with butter up, slips out of the hands, or slips off the table. In the process of slipping, it twists, flies in the air, and, finally, slaps on the table or on the floor. The initial stage of the fall is affected by a number of parameters: friction against the fingers or the surface of the table, the initial position of the sandwich and its initial speed, the height of the fall, and finally, the size of the sandwich. We have a dynamic system with several input parameters and one output - the position of the sandwich on the floor. Inside the system, as in the case of the coin, mechanical laws work, which are described by differential equations and they are deterministic. This means that there are no accidents in them - the result depends only on the input data, and if we exactly repeat the parameters, we should get identical results. This refers to a sandwich model presented as a system of differential equations, but what about real sandwiches, rough and unique, dropped by real people in restaurants, on the street, or on the couch? The variability of the real world can be described by applying random parameters to the input of the deterministic system.
However, even an algebra of random variables, which includes only addition and multiplication, is not easy, but we have differential equations! We will not get into this fascinating jungle, but use the well-developed technique in many areas - the Monte-Carlo method. It consists in the accumulation of statistics and in the determination of the properties of a certain complex system as a result of repeated tests with various random parameters. I stress once again: the system under investigation is not stochastic and not chaotic, and it reacts predictably to random input data. In the Monte-Carlo method, randomness is needed only in order to effectively sort through as many options as possible and look into all realistic “corners”, gaining insight into the behavior of the system.
Essentially, we have already used this method, watching the cyclists on the hill and still will use arranging deadlines in the office, and sharing money in a closed society. The one-to-one correspondence between probability and a measure of volume or area, which we talked about earlier, allows us to use the Monte Carlo method for numerical integration. The peculiarity of the upcoming experiment with a sandwich is that we will be interested not in the probability distribution (exact or empirical), but in the dependence of the probability on the parameters of the problem. We will look for the answer to the question: under what circumstances is the law of the sandwich executed? We will feed various specific parameters to the input of our dynamic system and collect statistics on oil drops up and oil down. In this way,
I’m convinced that intentionally dropping real sandwiches on the floor is wrong, so we’ll use mathematical modeling. To solve the problem of the fall of a sandwich, I chose one of the available simulators of the physical world that are used to create online games. He allowed to create a virtual table and floor, as well as two sandwiches. One turned out to be on the edge of the table, and the second - “slipped out of the fingers”, that is, slipped from the point support. In my power to set the initial position and angle of the sandwich, the horizontal speed (the case of brushing the sandwich off the table), the friction coefficients, the size of the sandwich and the height of the fall. Experiments look something like this:
 Experiments with the fall of the virtual sandwiches in the simulator of the physical world.
Experiments with the fall of the virtual sandwiches in the simulator of the physical world.
The moment the sandwich touches the floor, the angle of the sandwich is fixed, or rather, the angle of the vector normal to it. About which side the oil turned out to be, we are told by the sine of this angle: a good case corresponds to a good case, and a negative one is positioned oil down. The result is entered in the table, and the new virtual sandwich is ready to fall. We will set the following task: to estimate the probability of a butter sandwich falling down when it falls from a given height.
The Monte Carlo method implies that random variables are used as parameters. And here it is worth saying a few words about what a random variable is.. Let's return to mathematicians and mathematical structures. What structure can simulate the results of falling numbers on the dice, or the water level in the river, because there is constant excitement on the water? How to work with the number of cars passing the intersection for an hour? What structure can describe the state of the electron? On the one hand, these are concrete numbers from a well-defined set of values: for a bone, for example, from a set , and this value is easy to obtain by conducting an experiment. However, a repeated experiment will give a different result; this is clearly not just a number: today it’s one, tomorrow it’s another. There may even be a philosophical question: does it make sense to talk about some exact meaning of the “water level in the river”, or the number of cars, because these values cannot be “caught” and fixed? Can there be with any sense an exact knowledge of a random variable?
, and this value is easy to obtain by conducting an experiment. However, a repeated experiment will give a different result; this is clearly not just a number: today it’s one, tomorrow it’s another. There may even be a philosophical question: does it make sense to talk about some exact meaning of the “water level in the river”, or the number of cars, because these values cannot be “caught” and fixed? Can there be with any sense an exact knowledge of a random variable?
Often, speaking of such random variables, they are limited to only the average value, but this is a great way to get confused or even deliberately confuse. Two numbers: mean and standard deviation, is already better, but this is clearly not all the information about the object of interest. Maybe these are not numbers, but sets? Say, the water level in a river can be tried to describe the interval of possible values, taking into account the excitement, and for an example with cars one can say that from 1 to 100 cars travels in an hour, etc. But it is easy to see that the set of possible values is also not enough, for example, if you repeatedly measure the number of cars on the street, some numbers will occur more often, and some we will not wait at all. In the last chapter, we introduced a measure of probability, as a function on a probability space.probability distributionfor this value. And this is already exhaustive and accurate information. The function can be represented analytically or as an approximation by another function, in the form of a table, a histogram, or in the form of a graph. All these representations are models of the same object - a random variable, and the most important thing here is not so much a specific kind of representation, as the mathematical properties of this function. For probability distributions, properties are different: the number of parameters, the number of modes, entropy, infinite divisibility, additivity, stability, integrability, and so on. Modeling an unknown random variable obtained from an experiment, the statistician from a huge arsenal of known distributions with precisely defined properties chooses not so much the “most similar” function as the function, most fully coincides in properties with the observed random variable. This is the essencestatistical analysis and techniques for testing statistical hypotheses that are familiar to every student who has touched mathematical statistics.
We now have a task, in some sense, the opposite. We need to set sandwich parameters with random variables, not having statistical data, but following the necessary properties of these quantities. This is an important and interesting part of the Monte Carlo method, on which both the solution and its correctness depend.
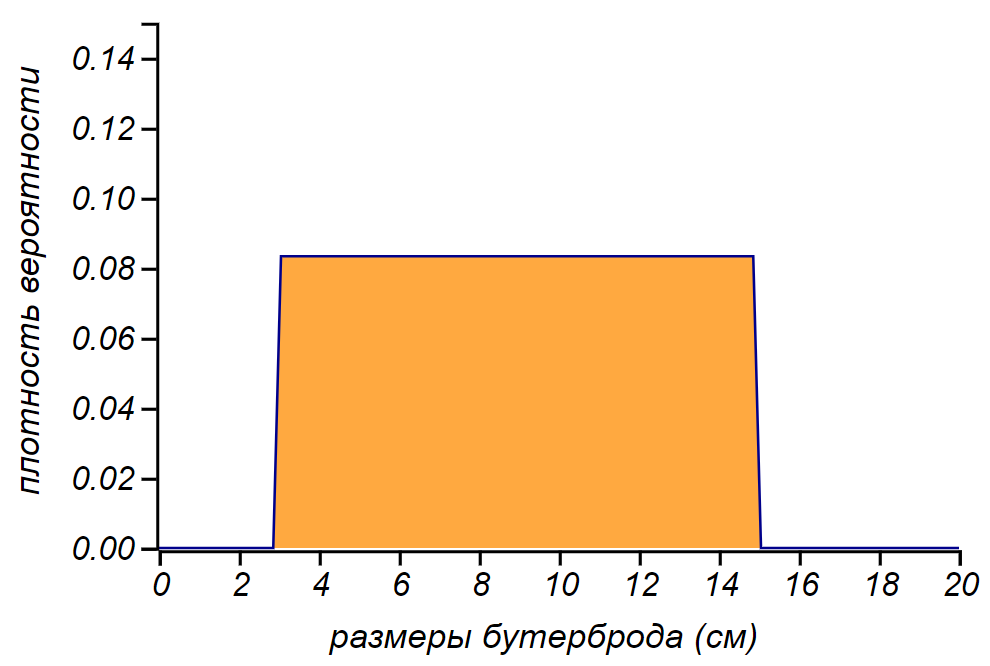 1. The size of the sandwich. What can they be? A reasonable size canape has a centimeter
1. The size of the sandwich. What can they be? A reasonable size canape has a centimeter wide, and the student's good "bast" can be centimeters
wide, and the student's good "bast" can be centimeters  . Most often, sandwiches are sized from
. Most often, sandwiches are sized from before
before  see. The probability of meeting a millimeter or meter width sandwich is, in a practical sense, zero. I cannot say anything more about sandwiches and will accept the size of the sandwiches evenly distributed in the specified range. The choice is not ideal, yet normal sandwiches we often meet tiny or giant. But later we will see that this weak point can be gracefully circumvented.
see. The probability of meeting a millimeter or meter width sandwich is, in a practical sense, zero. I cannot say anything more about sandwiches and will accept the size of the sandwiches evenly distributed in the specified range. The choice is not ideal, yet normal sandwiches we often meet tiny or giant. But later we will see that this weak point can be gracefully circumvented.
2. Initial position. Here, without further thinking, we will set a uniform distribution for shifting the sandwich over the edge of the table, if only it would fall.
 3. Coefficient of friction. This is a dimensionless quantity that depends only on the material. Tables and tablecloths are different, fingers squeeze a sandwich with different strength. Coefficient range from
3. Coefficient of friction. This is a dimensionless quantity that depends only on the material. Tables and tablecloths are different, fingers squeeze a sandwich with different strength. Coefficient range from before
before  , while extreme values are unlikely, on average we can expect something around
, while extreme values are unlikely, on average we can expect something around  . Any bell-shaped asymmetrical distribution of a non-negative magnitude, such as a gamma distribution or a log-normal, will help us .
. Any bell-shaped asymmetrical distribution of a non-negative magnitude, such as a gamma distribution or a log-normal, will help us .
 4. Starting speed. We rarely run sandwiches at high speed, and most often we don’t throw them at all, but brushing does happen. About the magnitude of the speed it is known only that it is positive and it can be assumed that when we brush on average we move as well as our hands move on average, that is, at a speed of about
4. Starting speed. We rarely run sandwiches at high speed, and most often we don’t throw them at all, but brushing does happen. About the magnitude of the speed it is known only that it is positive and it can be assumed that when we brush on average we move as well as our hands move on average, that is, at a speed of about m / s If only this is known about the value, then it is reasonable to describe it by an exponential distribution (why, we will talk later when we learn about the entropy of distributions). Its mode is zero, so the proportion of sandwiches that fell without a large initial speed will be quite decent. In the "tail" will be sandwiches, inadvertently launched into the flight while brushing crumbs off the table.
m / s If only this is known about the value, then it is reasonable to describe it by an exponential distribution (why, we will talk later when we learn about the entropy of distributions). Its mode is zero, so the proportion of sandwiches that fell without a large initial speed will be quite decent. In the "tail" will be sandwiches, inadvertently launched into the flight while brushing crumbs off the table.
5. We will fix the height of the table, drop a hundred sandwiches from it, count the number of fallen butter down and put it in a table, or reflect on the graph the probabilities of height.
Here, what are the probabilities of dropping a buttered sandwich down?
 The probability of landing butter down different sandwiches with different conditions depending on the height of the fall. For each height was held
The probability of landing butter down different sandwiches with different conditions depending on the height of the fall. For each height was held tests.
tests.
Some tendency is visible, but there is a very large scatter. When averaging, it turns out that the probability of the height of the fall is almost independent and barely more than half. Can you trust such an experiment? Does he refute the law of the sandwich? Maybe we didn’t throw a lot of sandwiches enough - noisy data turned out! Let's increase the number of throws, and see what happens:
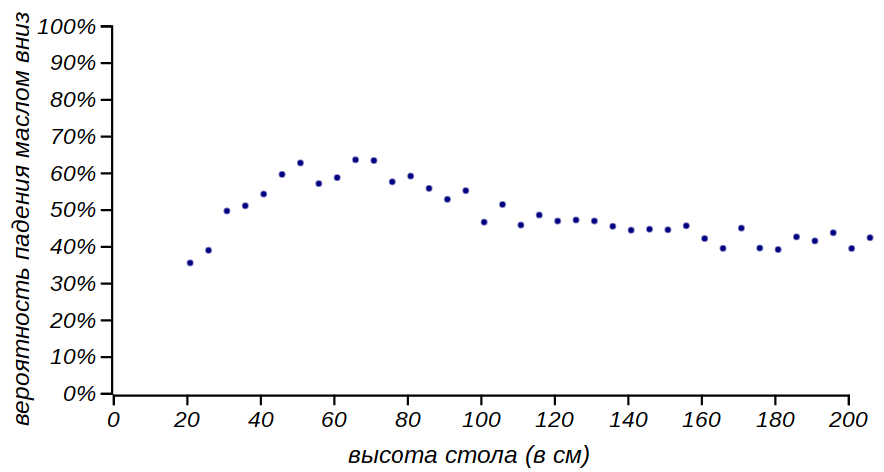 The probability of oil landing down different sandwiches counted for a larger number of tests (500 for each height).
The probability of oil landing down different sandwiches counted for a larger number of tests (500 for each height).
Emissions became less, but even more clearly shows that the law of the sandwich is very, very weak. But did we perform our experiments correctly? The Monte Carlo method looks temptingly simple: know yourself substitute what kind of data and see what happens. Mathematics is an honest thing: what kind of question is it ready to give what answer is . But whether this answer makes sense strongly depends on the question.
Before embarking on experiments, not so toy as ours, but real and expensive, using an orbiting satellite, an elementary particle accelerator or a thousand real butter sandwiches, it is necessary to carry out preparatory work. And one of the powerful and beautiful ways to understand how to conduct an experiment correctly is the analysis of the dimensions of the problem.
We modeled the sandwich with generalized coordinates, momenta and forces - physical quantities, which, in turn, are related by equations of analytical mechanics. In physics, the quantitative quantities with which we deal, which we measure and substitute into equations, do not “fit” into ordinary numbers — they have an additional structure, which is called the dimension. Not all valid mathematical expressions make sense if dimensional values are involved. Let's say it makes no sense to add speed and mass, it is impossible to compare force and distance. However, one can consider the product of velocity and mass, obtaining a new dimensional quantity — the amount of motion, or momentum; You can square the speed and divide it by distance, thus obtaining a value that has the dimension of acceleration.
Dimension analysis and similarity theory were born long ago, since the days of Lord Rayleigh. They are used in mechanics, electrodynamics, astrophysics and cosmology, allowing with a frightening elegance to approach the solution of complex problems. However, research in this area has not been completed and the rigorous definitionthe structure formed by quantitative (dimensional) values was given only in 2016 by the Spanish mathematician Alvaro Raposo.
The limitations imposed by the dimensions on physical formulas are often perceived by pupils and students as an extra hassle to follow. But on the other hand, logically agreed restrictions are extremely useful! They exclude incorrect expressions, they allow one to “foresee” the structure of solving a physical problem before its detailed solution, they are a powerful tool in planning and analyzing experimental data.
But what is interesting. We calculated the fall of the sandwich in the program, using ordinary and not dimensional numbers. How can one “clear” a physical quantity from a dimension and turn it into a number? For this we serve well to usunits of measurement of physical quantities: all these meters, pounds, minutes and newtons. The units of measurement assume the dimensional part of the value, leaving us a multiplier - a real number, which the computer can already deal with. For example, the speed in the chosen direction is km / h can be represented by number
km / h can be represented by number  . But there is a subtlety: the numerical representation depends on the choice of units. When selecting other units (say, meters and seconds) , the same speed will be represented by a different number:
. But there is a subtlety: the numerical representation depends on the choice of units. When selecting other units (say, meters and seconds) , the same speed will be represented by a different number: . The numbers are different, but the value is one, and it does not depend on our choice of any units.
. The numbers are different, but the value is one, and it does not depend on our choice of any units.
The question arises: is there in any sense the "best" system of units? It turns out that it exists; for this, when solving a problem, it is necessary to use the dimensional quantities included in the task as units of measurement.
In this chapter we have sandwiches flying, in the previous one coins were flying, let us give one more flying example. How should the flight characteristics of different birds be compared? It is clear that the speeds that the birds develop are different: in a pigeon - km / h, near the swift -
km / h, near the swift -  km / h, in crane, sparrow or mallard -
km / h, in crane, sparrow or mallard -  km / h, at a hummingbird -
km / h, at a hummingbird -  km / h But all these birds differ significantly in size and manner of flight. If the length of a parrot is measured in parrots, and time - in periods of flapping of its wings, one can get some, as they say, own speed . You can divide the speeds that these birds can develop into their own values and get a dimensionless speed, which shows how many hull lengths a bird can move in one wing stroke. Here's what happens with this comparison:
km / h But all these birds differ significantly in size and manner of flight. If the length of a parrot is measured in parrots, and time - in periods of flapping of its wings, one can get some, as they say, own speed . You can divide the speeds that these birds can develop into their own values and get a dimensionless speed, which shows how many hull lengths a bird can move in one wing stroke. Here's what happens with this comparison:
It can be seen that the swift is rightfully considered the best flyer, but the hummingbird does not use energy efficiently, however, this bird does not have the task to fly for a long time, like a pigeon. The identical absolute speeds of the crane, sparrow and duck differ significantly when converted to dimensionless quantities. This kind of calculations are used to simulate a real big plane, testing a small model in a wind tunnel. If all the dimensionless parameters of these two systems are close, they can be considered physically similar and modeling makes sense. We have already used this approach, reflecting relative units instead of absolute ones in the Lorentz diagrams. This allowed us to compare different phenomena and distributions.
It is clear what will be the most suitable system of units in the analysis of the flight of a sandwich. Of course, the length should be measured in sandwiches. Per unit of time you can take the value where
where  - the length of the sandwich, and
- the length of the sandwich, and  - acceleration of gravity. And the height of the table should not be measured in meters, but in its own units. Having thus obtained the result, we can immediately generalize it both to the case of a canape and to a solid “bast shoe”. So, we repeat the calculations, but on the graph we will reflect the height of the table in relative units. If we did everything right, then for two sandwiches of different sizes we should get very similar graphics. Let's check it out:
- acceleration of gravity. And the height of the table should not be measured in meters, but in its own units. Having thus obtained the result, we can immediately generalize it both to the case of a canape and to a solid “bast shoe”. So, we repeat the calculations, but on the graph we will reflect the height of the table in relative units. If we did everything right, then for two sandwiches of different sizes we should get very similar graphics. Let's check it out:
 The probability of an oil landing down a sandwich of a certain fixed value, at different heights of incidence, calculated in relative units. Blue dots correspond to a sandwich size of 5 cm, red - 10 cm.
The probability of an oil landing down a sandwich of a certain fixed value, at different heights of incidence, calculated in relative units. Blue dots correspond to a sandwich size of 5 cm, red - 10 cm.
In the original formulation, we went through different sizes and obtained a cloud of results, in which the dependence of interest was hidden. With the increase in the number of tests, we averaged this cloud and received an uninteresting answer. To show more clearly what the methodological mistake was, imagine that we want to calculate the probability of the butter falling down, turning randomly both the initial conditions and the size of the sandwich and the height. This is equivalent to averaging all the results we obtained at once. As a result, we will get a confident middle point - the probability is very close to as when tossing a coin! This is a very logical and expected result, but it is completely uninteresting. Averaging a lot of data for different sizes, we have already come close to this conclusion. But if the purpose of modeling is to identify patterns, then it makes sense to minimize the number of parameters.
as when tossing a coin! This is a very logical and expected result, but it is completely uninteresting. Averaging a lot of data for different sizes, we have already come close to this conclusion. But if the purpose of modeling is to identify patterns, then it makes sense to minimize the number of parameters.
The cleared data now clearly speak in favor of the law of meanness, limiting it, however, to a certain range of heights: from before
before  the size of the sandwich (from the height of the elbow above the table to the height of the arm of a standing person). Outside of this range, a sandwich has a higher chance of turning the right side before falling.
the size of the sandwich (from the height of the elbow above the table to the height of the arm of a standing person). Outside of this range, a sandwich has a higher chance of turning the right side before falling.
And what if you look further and throw sandwiches out of the window? It is clear that when falling from a great height, it doesn’t matter which side fell what turned into a sandwich, and air resistance stabilizes the fall, but theoretically, what do we expect to see? Probably, some fluctuations of probability should be observed with increasing flight time. Let's get a look:
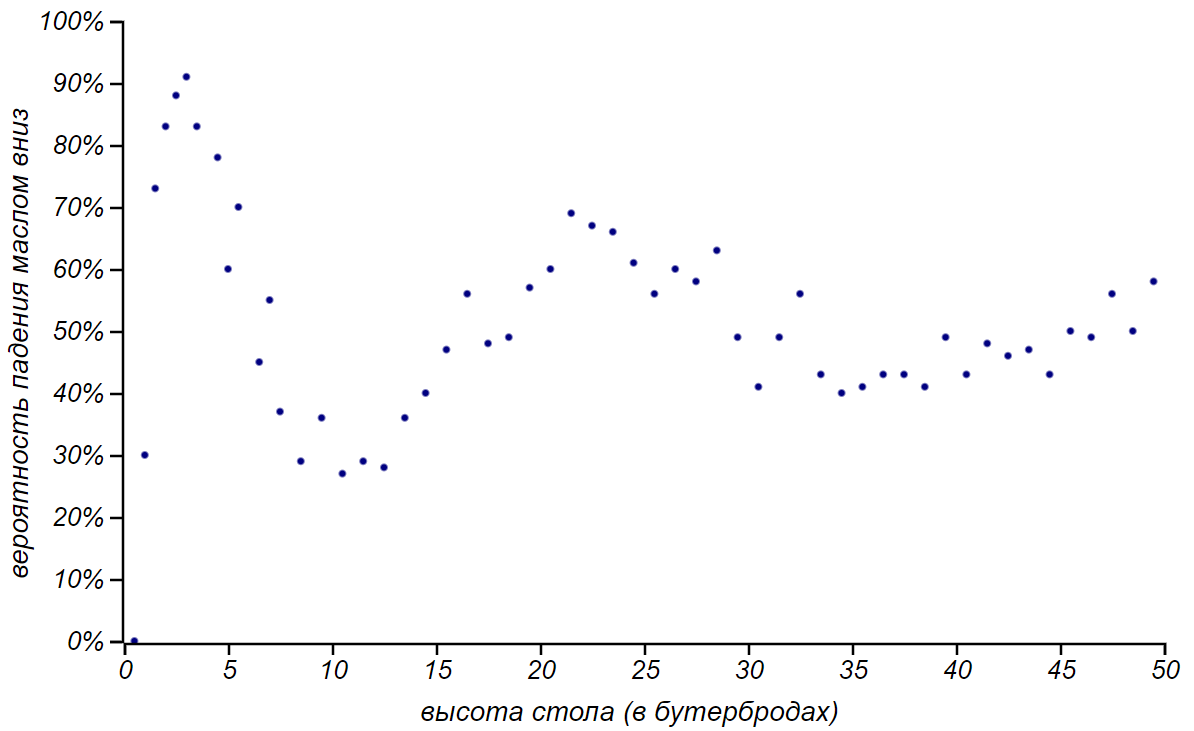 The likelihood of landing the butter down a sandwich when falling from a great height.
The likelihood of landing the butter down a sandwich when falling from a great height.
We guessed with frequency, but it is curious that the amplitude decreases, and the fluctuations of probability converge to . What can it say? Is this the same effect as in the case of a coin, when the consequences of deviations of the initial conditions become more significant with an increase in the duration of the flight? It turns out that in this case the nature of the leveling of probabilities is different.
. What can it say? Is this the same effect as in the case of a coin, when the consequences of deviations of the initial conditions become more significant with an increase in the duration of the flight? It turns out that in this case the nature of the leveling of probabilities is different.
No matter how frivolous the topic of our book is, we speak the language of mathematics, and he is striving for exact solutions. The Monte Carlo method allowed us to get an idea of the solution, but this was what is called brute force. It is not as interesting as any analytical solution. Dimension analysis will allow us to obtain the theoretical form of the dependence obtained by the Monte Carlo method. To do this, we do not need to solve differential equations, moreover, all our reasoning does not go beyond the limits of quite primitive and obvious relations. This is the charm of dimensional analysis, which, incidentally, sometimes looks like fiction. So let's start, limiting for simplicity just sliding the length of the sandwich from the height table
from the height table  with zero horizontal speed.
with zero horizontal speed.
1. The angle of rotation of the falling sandwich depends on the time and angular velocity:
2. The angular velocity equal to the product of the time of sliding and angular acceleration:
3. The creeping time can be expressed in terms of the acceleration of free fall and part of the length of the sandwich, which was in contact with the table with the following proportion: - the length of the sandwich lying on the table. Here we use the proportionality relation indicated by
- the length of the sandwich lying on the table. Here we use the proportionality relation indicated by . Expression
. Expression can be replaced by
can be replaced by  where
where  - some unknown constant. I love this relationship very much. Proportionality "absorbs" all that is complex, which turns into a constant: the fact that when turning changes the moment of gravity, and that during sliding, the center of rotation changes. All this, of course, you need to know for an exact calculation, but the result will be just a dimensionless coefficient, and it does not matter in our analysis. With one badge we saved ourselves from tedious integration.
- some unknown constant. I love this relationship very much. Proportionality "absorbs" all that is complex, which turns into a constant: the fact that when turning changes the moment of gravity, and that during sliding, the center of rotation changes. All this, of course, you need to know for an exact calculation, but the result will be just a dimensionless coefficient, and it does not matter in our analysis. With one badge we saved ourselves from tedious integration.
4. Angular acceleration comes from the acceleration of gravity and depends on the shoulder, to which the force of gravity is attached: allowed us not to calculate the moment of inertia of the plate for the axis lying in its plane, as well as the changing projection of gravity (these are two more integrals).
allowed us not to calculate the moment of inertia of the plate for the axis lying in its plane, as well as the changing projection of gravity (these are two more integrals).
5. Finally, the fall time depends on the height of the table and the acceleration of gravity:
6. Substituting all these expressions in the first formula, we get a simple result:
 and
and  . Well, everything converges - the angle is dimensionless and it depends on dimensionless coefficients. This angle does not depend on the time scale; pure geometry remains. The denominator is not dangerous when
. Well, everything converges - the angle is dimensionless and it depends on dimensionless coefficients. This angle does not depend on the time scale; pure geometry remains. The denominator is not dangerous when the sandwich will not fall at all (we consider zero horizontal speed), so
the sandwich will not fall at all (we consider zero horizontal speed), so  .
.
Which side the sandwich drops is determined by the sign of the sine of the angle that is, a function
that is, a function  . This function returns
. This function returns for the case of "oil up" and
for the case of "oil up" and  for "oil down." We can use this function to express the probability of a deterministic sandwich falling if we bring it to the range from
for "oil down." We can use this function to express the probability of a deterministic sandwich falling if we bring it to the range from before
before  :
:  appearing in the probability formula expresses all that remains hidden with the help of the sign of proportionality. It was, indeed, a very cunning move, it saved us from tedious integration, (and even three), but how do we now know what this coefficient is equal to? From the experiment, and one single experiment with measuring the angle at the time of the fall is enough to get an estimate of this value! Using a simulator, I easily found out that
appearing in the probability formula expresses all that remains hidden with the help of the sign of proportionality. It was, indeed, a very cunning move, it saved us from tedious integration, (and even three), but how do we now know what this coefficient is equal to? From the experiment, and one single experiment with measuring the angle at the time of the fall is enough to get an estimate of this value! Using a simulator, I easily found out that .
.
The next task is to express mathematically that the initial positions may be different. We are interested in the likelihood that the sandwich will drop butter down, if
may be different. We are interested in the likelihood that the sandwich will drop butter down, if will be equal
will be equal  or
or  or any number from
or any number from  before
before  . We used the “or” union, with each of these cases being considered by us as independent and excluding all others when conducting a specific experiment. Recall that probability is a measure of probability space, and if so, then probability is additive. This allows us to simply add up the probabilities.
. We used the “or” union, with each of these cases being considered by us as independent and excluding all others when conducting a specific experiment. Recall that probability is a measure of probability space, and if so, then probability is additive. This allows us to simply add up the probabilities. for all values
for all values  by multiplying from the preliminarily the probability of falling into a specific range of values. We divide the segment from
by multiplying from the preliminarily the probability of falling into a specific range of values. We divide the segment from before
before  on
on  parts, and calculate the probability estimate as a sum:
parts, and calculate the probability estimate as a sum: expresses probability for a random variable
expresses probability for a random variable  get into the width segment
get into the width segment  . Here is the result for a significant number of splits (
. Here is the result for a significant number of splits ( ) and a series of numerical experiments with zero horizontal velocity:
) and a series of numerical experiments with zero horizontal velocity:
 Theoretical and experimental estimate of the likelihood of an oil landing down a sandwich when falling from a great height. The initial horizontal velocity in the experiments is zero.
Theoretical and experimental estimate of the likelihood of an oil landing down a sandwich when falling from a great height. The initial horizontal velocity in the experiments is zero.
The solution we gave before contains more random parameters, so it turned out to be more smooth and close to . But, in principle, a dimension analysis can be carried out for a more general case.
. But, in principle, a dimension analysis can be carried out for a more general case.
Note that the probability approaching with increasing
approaching with increasing  to values close to
to values close to  . And this is not at all due to the uncertainty and influence of the initial errors. The calculations showed that this is the result of adding the set of harmonics formed by the values
. And this is not at all due to the uncertainty and influence of the initial errors. The calculations showed that this is the result of adding the set of harmonics formed by the values when summing up
when summing up  . If we forget about the unfortunate sandwich and continue the schedule
. If we forget about the unfortunate sandwich and continue the schedule then we will see that the probability estimate will continue to fluctuate near
then we will see that the probability estimate will continue to fluctuate near  gradually striving for this value.
gradually striving for this value.
Is it possible to find out without direct calculations, whether the probability will continue to converge to or ever grow again? And in this phenomenon there is also a place for non-trivial and deep mathematics. The fact is that each value
or ever grow again? And in this phenomenon there is also a place for non-trivial and deep mathematics. The fact is that each value corresponds to a certain oscillation frequency, and the whole set forms the so-called spectrum of the total function. If the spectrum is discrete, that is, consists of individual frequencies, then the total function (it is called the Fourier transform) will be periodic. Continuous spectrum in the form of a constant in the segment from
corresponds to a certain oscillation frequency, and the whole set forms the so-called spectrum of the total function. If the spectrum is discrete, that is, consists of individual frequencies, then the total function (it is called the Fourier transform) will be periodic. Continuous spectrum in the form of a constant in the segment from before
before  will correspond to aperiodic function, similar to decreasing oscillations. But we looked at a new branch of mathematics - in functional analysis .
will correspond to aperiodic function, similar to decreasing oscillations. But we looked at a new branch of mathematics - in functional analysis .
The great Enrico Fermi, the grandfather of the Monte Carlo method (the father is considered a mathematician Stanislav Ulam), taught his students to do simple evaluative calculations, to estimate on a piece of paper or on fingers, what we expect to get before starting to solve the problem exactly. It is great that if the assessment turns out to be true, it will become clear that the essence of the problem is captured, but if not, then this is all the more useful result - it means that the task turned out to be more interesting than it seems!
In our case, a simple assessment is quite enough; the problem of a sandwich is not worth a more thorough solution. The Monte-Carlo method showed us only a hint of the solution, and the dimension analysis showed only some of its general structure, but together they could show us how the required probability is arranged. Erudition allows mathematics to see ready-made structures in the solutions and make far-reaching assumptions and conclusions.
Robert Matthews, in his landmark study, also used dimensional analysis to show that the law of the sandwich is fundamental. His conclusion is based on the fact that the limiting height of an organism that has risen to the hind limbs with the goal of the forelimbs is to take a sandwich with butter is determined by the strength properties of biological tissues and gravity. In turn, the characteristic size of a sandwich should be consistent with the scale of the creature - and dwarfs on some heavy planet and little dalds on a planet with low gravity will choose their sandwiches in size. Here we come to what in science is called speculation. This is not a resale of any good at exorbitant prices, but dubious assumptions that form the basis of a logical construction. In particular, we assume creatures have hands that have proportions similar to ours, and this is more than debatable.
In merphology, there is a well-known quotation of the law X.L. Menkina Group:
As children we were amused by throwing high up the pigeon wing feather or tail feather, stuck in a piece of clay, a centimeter or two in diameter. It flew four meters, and then beautifully and smoothly descended to autorotation, like a helicopter with a muffled engine. Then we grew up, and our fun became less harmless. We got a nut and screwed in two bolts from opposite sides, pressing the stuffing from the stitched match heads. It was necessary to tie a ribbon or just a piece of rope to one of the bolts, properly unwind and launch into the sky about fifteen meters. In the fall, the lightweight tape stabilized the vertical position of the projectile, providing a quality impact on the asphalt and a small explosion, sometimes tearing the nut to pieces. (Be careful if you decide to share this childhood experience with your children!)
In both experiments, we see that a light feather or ribbon quickly turned out to be over the hard part of the apparatus and stabilized the fall. This, apparently, leads to the intuitive opinion that heavy butter and light bread should also behave in this way. Imagine a balloon: a denser basket is always located below a dense balloon. Moreover, experience suggests that if you take two fingers to the geometric center of an object with an asymmetrically distributed mass, it will tumble so that the heavy part is at the bottom.
But both of these phenomena do not work in the case of a falling sandwich.
Let's start with the second process - with “outweighing”. It was not by chance that I said boringly: "... if you take up the geometricthe middle of the object .. ", it is meant here that the touch points lie on a certain straight line forming the axis of rotation passing through the center of gravity of the object. In this case, the stable position will be such that the center of gravity is lower than the axis. But if formed by the fingers, the axis of rotation passes through the center of gravity, the system will be in indifferent balance - it will not care how it is oriented.
What makes a feather-weir, a bomb made of a nut, or a balloon with aeronauts in a basket make you orientate in the “right” way? Air. It “holds” our objects so that the axis passes above the center of gravity. More precisely, the oncoming flow of air, creating a force distributed over the area of the body. And the conditional point of application of this force will be located near the geometric center of the area of the figure. To make it clearer, let's draw the forces acting on a conditional balloon as an object with an uneven density:
 Forces that lead the balloon to a stable position.
Forces that lead the balloon to a stable position.
And what's a sandwich?
First, if we “turn off” the air, it will just fall. In free fall, the body rotates precisely around the center of mass, so that it has no reason to turn in any particular way. As they say in school: "Weightlessness is observed in a falling elevator." The butter on the sandwich is just as "weightless."
Dense oil can affect the process of slipping, it will effectively raise the center of mass above the exact touch and change in the expression for the angular acceleration on
on  where
where  - the relative thickness of the sandwich. For small values
- the relative thickness of the sandwich. For small values this expression can be calculated as
this expression can be calculated as  . We get, as they say, a second-order effect. For a sandwich with a width to thickness ratio like
. We get, as they say, a second-order effect. For a sandwich with a width to thickness ratio like to
to  relative changes do not exceed
relative changes do not exceed  . And this is the maximum upper limit of the effect, because we raised the center of mass by the thickness of the sandwich, which corresponds to infinitely dense butter!
. And this is the maximum upper limit of the effect, because we raised the center of mass by the thickness of the sandwich, which corresponds to infinitely dense butter!
Now "turn on" the air back, leaving the density of butter infinitely greater than the density of bread. We have a thin dense plate with a weightless, but air-resisting “parachute”. As long as the sandwich plane is horizontal or so, a moment of air resistance forces acts on it proportional to the sail area — the area with which the air flow interacts: . In the vertical position, the windage will decrease and, accordingly, the moment will be different:
. In the vertical position, the windage will decrease and, accordingly, the moment will be different: . The ratio of these moments:
. The ratio of these moments: I wrote a sign of proportionality here, because the drag coefficients for a plate located across and along the stream are different, and they are unknown to me. But they are not needed - it is already clear that the influence of air in the vertical position (namely, it makes the oil position unequal) is weaker than in the horizontal one. And now let us remember that the sandwich is rotating, which means that it is substituted to the stream either face up, then a plane. We can introduce a measure of action of resistance forces. If the angular velocity of rotation does not significantly change in one period (and this is so for air), then it makes sense to take as a measure the change in angular momentum proportional to the time of the force. In turn, the period of action is proportional to the angle “swept up” by the sandwich during this period. In sum, the action measures of moments
I wrote a sign of proportionality here, because the drag coefficients for a plate located across and along the stream are different, and they are unknown to me. But they are not needed - it is already clear that the influence of air in the vertical position (namely, it makes the oil position unequal) is weaker than in the horizontal one. And now let us remember that the sandwich is rotating, which means that it is substituted to the stream either face up, then a plane. We can introduce a measure of action of resistance forces. If the angular velocity of rotation does not significantly change in one period (and this is so for air), then it makes sense to take as a measure the change in angular momentum proportional to the time of the force. In turn, the period of action is proportional to the angle “swept up” by the sandwich during this period. In sum, the action measures of moments and
and  will be proportional
will be proportional  and
and  where the corners that sweep the end and the plane are shown in the drawing.
where the corners that sweep the end and the plane are shown in the drawing. 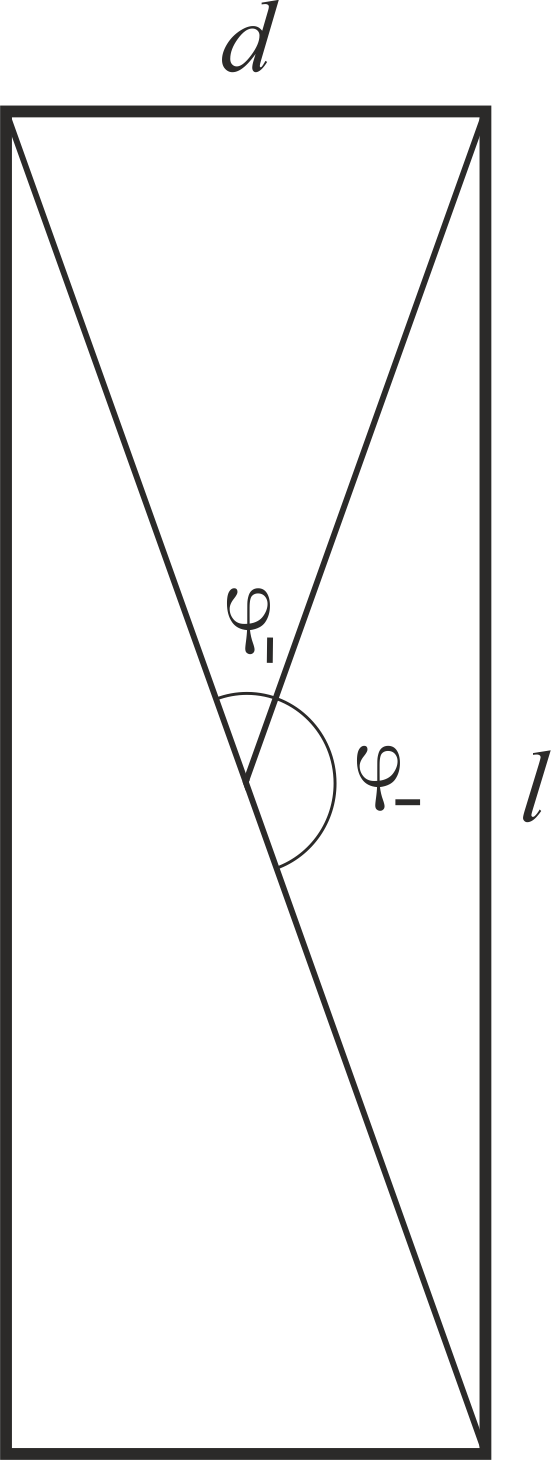 We could use the work of the resistance forces as a measure and would get the same ratio. The angle ratio is easy to calculate:
We could use the work of the resistance forces as a measure and would get the same ratio. The angle ratio is easy to calculate: ,
,  (use the property of a small angle tangent that runs from
(use the property of a small angle tangent that runs from  accuracy at angles less
accuracy at angles less  ), which means we have:
), which means we have:  .
.
If it seemed to the reader that we were now firing from a cannon on sparrows, then I completely agree with him. But, firstly, I don’t want to hear more about the “outweighing” oil, secondly, I don’t want to be unfounded, and thirdly, I wanted to show how the physicist assesses values, representing the process, but not having complete data. Of course, at the moment of landing, the oil can stick to the floor and prevent the sandwich from jumping up and rolling over again, but I certainly will not disassemble the mechanics of the impact, elastic deformation and jump of a piece of bread. So there was a bit of analysis for this problem. And the second Nobel for her will not give.
The goal of our path was not so important: a refutation or justification of the law of a sandwich, as the path itself. He showed how the combination of different mathematical methods allows us to look at the problem from different angles and gives a fairly accurate knowledge, even without a detailed solution of the problem. In the consistency of various mathematical disciplines, approaches and points of view is the strength and beauty of mathematics. It is appropriate to recall the wonderful words of Marina Tsvetaeva: “I don’t want to have a point of view, I want to have a sight” . The study of various areas of mathematics is able to give the researcher a real “three-dimensional” multidimensional vision, which allows you to look into the seemingly closed and hidden space of knowledge.
Published chapters:
• Introduction to merphology
• Accidents are not accidental?
• The dizzying flight of a butter sandwich
• The law of the watermelon rind and the normality of the abnormality
• The law of the zebra and another's line
• The director’s curse and damned printers
• Thermodynamics of class inequality
• Accidents are not accidental?
• The dizzying flight of a butter sandwich
• The law of the watermelon rind and the normality of the abnormality
• The law of the zebra and another's line
• The director’s curse and damned printers
• Thermodynamics of class inequality

In this chapter, we look at the law of the sandwich and organize the whole study using the Monte Carlo method, and the analysis of dimensions. And finally, we will debunk the popular myth that it is oil that is the cause of this law of meanness.
The theme of falling sandwiches does not rest either the general public or the researchers. For decades, experiments have been carried out, films are shot, articles are written, a falling sandwich acquires legends and wrong conclusions. Not only is this useless task attracted so much attention, and if you think that all this is self-indulgence, then keep in mind that even bonuses are given for its solution, but not serious ones either. In 1995, Robert Matthews received the Snobel Prize for his "Falling Sandwich, Murphy's Law and Fundamental Constants", published in the European Journal of Physics. Despite the comic topic and the corresponding reaction of the scientific community, this is a completely interesting article, which thoroughly analyzes the process of slipping, and makes a far-reaching conclusion: on whatever planet anthropomorphic creatures live in the atmosphere, they will be doomed to the law of the sandwich. After such a triumph of useless research, one could close the topic, but why miss the opportunity to consider interesting and objectively useful methods using the example of an amusing puzzle!
Ida throw sandwiches in Monte Carlo!
We seldom throw sandwiches like a coin, at least when we are older than two years. More often than not, we involuntarily repeat approximately the same experiment: a sandwich, originally placed with butter up, slips out of the hands, or slips off the table. In the process of slipping, it twists, flies in the air, and, finally, slaps on the table or on the floor. The initial stage of the fall is affected by a number of parameters: friction against the fingers or the surface of the table, the initial position of the sandwich and its initial speed, the height of the fall, and finally, the size of the sandwich. We have a dynamic system with several input parameters and one output - the position of the sandwich on the floor. Inside the system, as in the case of the coin, mechanical laws work, which are described by differential equations and they are deterministic. This means that there are no accidents in them - the result depends only on the input data, and if we exactly repeat the parameters, we should get identical results. This refers to a sandwich model presented as a system of differential equations, but what about real sandwiches, rough and unique, dropped by real people in restaurants, on the street, or on the couch? The variability of the real world can be described by applying random parameters to the input of the deterministic system.
However, even an algebra of random variables, which includes only addition and multiplication, is not easy, but we have differential equations! We will not get into this fascinating jungle, but use the well-developed technique in many areas - the Monte-Carlo method. It consists in the accumulation of statistics and in the determination of the properties of a certain complex system as a result of repeated tests with various random parameters. I stress once again: the system under investigation is not stochastic and not chaotic, and it reacts predictably to random input data. In the Monte-Carlo method, randomness is needed only in order to effectively sort through as many options as possible and look into all realistic “corners”, gaining insight into the behavior of the system.
Essentially, we have already used this method, watching the cyclists on the hill and still will use arranging deadlines in the office, and sharing money in a closed society. The one-to-one correspondence between probability and a measure of volume or area, which we talked about earlier, allows us to use the Monte Carlo method for numerical integration. The peculiarity of the upcoming experiment with a sandwich is that we will be interested not in the probability distribution (exact or empirical), but in the dependence of the probability on the parameters of the problem. We will look for the answer to the question: under what circumstances is the law of the sandwich executed? We will feed various specific parameters to the input of our dynamic system and collect statistics on oil drops up and oil down. In this way,
I’m convinced that intentionally dropping real sandwiches on the floor is wrong, so we’ll use mathematical modeling. To solve the problem of the fall of a sandwich, I chose one of the available simulators of the physical world that are used to create online games. He allowed to create a virtual table and floor, as well as two sandwiches. One turned out to be on the edge of the table, and the second - “slipped out of the fingers”, that is, slipped from the point support. In my power to set the initial position and angle of the sandwich, the horizontal speed (the case of brushing the sandwich off the table), the friction coefficients, the size of the sandwich and the height of the fall. Experiments look something like this:

The moment the sandwich touches the floor, the angle of the sandwich is fixed, or rather, the angle of the vector normal to it. About which side the oil turned out to be, we are told by the sine of this angle: a good case corresponds to a good case, and a negative one is positioned oil down. The result is entered in the table, and the new virtual sandwich is ready to fall. We will set the following task: to estimate the probability of a butter sandwich falling down when it falls from a given height.
The Monte Carlo method implies that random variables are used as parameters. And here it is worth saying a few words about what a random variable is.. Let's return to mathematicians and mathematical structures. What structure can simulate the results of falling numbers on the dice, or the water level in the river, because there is constant excitement on the water? How to work with the number of cars passing the intersection for an hour? What structure can describe the state of the electron? On the one hand, these are concrete numbers from a well-defined set of values: for a bone, for example, from a set
Often, speaking of such random variables, they are limited to only the average value, but this is a great way to get confused or even deliberately confuse. Two numbers: mean and standard deviation, is already better, but this is clearly not all the information about the object of interest. Maybe these are not numbers, but sets? Say, the water level in a river can be tried to describe the interval of possible values, taking into account the excitement, and for an example with cars one can say that from 1 to 100 cars travels in an hour, etc. But it is easy to see that the set of possible values is also not enough, for example, if you repeatedly measure the number of cars on the street, some numbers will occur more often, and some we will not wait at all. In the last chapter, we introduced a measure of probability, as a function on a probability space.probability distributionfor this value. And this is already exhaustive and accurate information. The function can be represented analytically or as an approximation by another function, in the form of a table, a histogram, or in the form of a graph. All these representations are models of the same object - a random variable, and the most important thing here is not so much a specific kind of representation, as the mathematical properties of this function. For probability distributions, properties are different: the number of parameters, the number of modes, entropy, infinite divisibility, additivity, stability, integrability, and so on. Modeling an unknown random variable obtained from an experiment, the statistician from a huge arsenal of known distributions with precisely defined properties chooses not so much the “most similar” function as the function, most fully coincides in properties with the observed random variable. This is the essencestatistical analysis and techniques for testing statistical hypotheses that are familiar to every student who has touched mathematical statistics.
We now have a task, in some sense, the opposite. We need to set sandwich parameters with random variables, not having statistical data, but following the necessary properties of these quantities. This is an important and interesting part of the Monte Carlo method, on which both the solution and its correctness depend.
 1. The size of the sandwich. What can they be? A reasonable size canape has a centimeter
1. The size of the sandwich. What can they be? A reasonable size canape has a centimeter2. Initial position. Here, without further thinking, we will set a uniform distribution for shifting the sandwich over the edge of the table, if only it would fall.
 3. Coefficient of friction. This is a dimensionless quantity that depends only on the material. Tables and tablecloths are different, fingers squeeze a sandwich with different strength. Coefficient range from
3. Coefficient of friction. This is a dimensionless quantity that depends only on the material. Tables and tablecloths are different, fingers squeeze a sandwich with different strength. Coefficient range from 4. Starting speed. We rarely run sandwiches at high speed, and most often we don’t throw them at all, but brushing does happen. About the magnitude of the speed it is known only that it is positive and it can be assumed that when we brush on average we move as well as our hands move on average, that is, at a speed of about
4. Starting speed. We rarely run sandwiches at high speed, and most often we don’t throw them at all, but brushing does happen. About the magnitude of the speed it is known only that it is positive and it can be assumed that when we brush on average we move as well as our hands move on average, that is, at a speed of about5. We will fix the height of the table, drop a hundred sandwiches from it, count the number of fallen butter down and put it in a table, or reflect on the graph the probabilities of height.
Here, what are the probabilities of dropping a buttered sandwich down?

Some tendency is visible, but there is a very large scatter. When averaging, it turns out that the probability of the height of the fall is almost independent and barely more than half. Can you trust such an experiment? Does he refute the law of the sandwich? Maybe we didn’t throw a lot of sandwiches enough - noisy data turned out! Let's increase the number of throws, and see what happens:

Emissions became less, but even more clearly shows that the law of the sandwich is very, very weak. But did we perform our experiments correctly? The Monte Carlo method looks temptingly simple: know yourself substitute what kind of data and see what happens. Mathematics is an honest thing: what kind of question is it ready to give what answer is . But whether this answer makes sense strongly depends on the question.
Before embarking on experiments, not so toy as ours, but real and expensive, using an orbiting satellite, an elementary particle accelerator or a thousand real butter sandwiches, it is necessary to carry out preparatory work. And one of the powerful and beautiful ways to understand how to conduct an experiment correctly is the analysis of the dimensions of the problem.
We modeled the sandwich with generalized coordinates, momenta and forces - physical quantities, which, in turn, are related by equations of analytical mechanics. In physics, the quantitative quantities with which we deal, which we measure and substitute into equations, do not “fit” into ordinary numbers — they have an additional structure, which is called the dimension. Not all valid mathematical expressions make sense if dimensional values are involved. Let's say it makes no sense to add speed and mass, it is impossible to compare force and distance. However, one can consider the product of velocity and mass, obtaining a new dimensional quantity — the amount of motion, or momentum; You can square the speed and divide it by distance, thus obtaining a value that has the dimension of acceleration.
Dimension analysis and similarity theory were born long ago, since the days of Lord Rayleigh. They are used in mechanics, electrodynamics, astrophysics and cosmology, allowing with a frightening elegance to approach the solution of complex problems. However, research in this area has not been completed and the rigorous definitionthe structure formed by quantitative (dimensional) values was given only in 2016 by the Spanish mathematician Alvaro Raposo.
The limitations imposed by the dimensions on physical formulas are often perceived by pupils and students as an extra hassle to follow. But on the other hand, logically agreed restrictions are extremely useful! They exclude incorrect expressions, they allow one to “foresee” the structure of solving a physical problem before its detailed solution, they are a powerful tool in planning and analyzing experimental data.
But what is interesting. We calculated the fall of the sandwich in the program, using ordinary and not dimensional numbers. How can one “clear” a physical quantity from a dimension and turn it into a number? For this we serve well to usunits of measurement of physical quantities: all these meters, pounds, minutes and newtons. The units of measurement assume the dimensional part of the value, leaving us a multiplier - a real number, which the computer can already deal with. For example, the speed in the chosen direction is
The question arises: is there in any sense the "best" system of units? It turns out that it exists; for this, when solving a problem, it is necessary to use the dimensional quantities included in the task as units of measurement.
In this chapter we have sandwiches flying, in the previous one coins were flying, let us give one more flying example. How should the flight characteristics of different birds be compared? It is clear that the speeds that the birds develop are different: in a pigeon -
| bird | speed, km / h | body length | stroke frequency, 1 / s | own speed, m / s | dimensionless speed |
|---|---|---|---|---|---|
| swift | 140 | 18 cm | five | 0.9 | 43 |
| post pigeon | 90 | 30 cm | five | 1.5 | 17 |
| hummingbird | 80 | 8 cm | 200 | sixteen | 1.4 |
| crane | 50 | 1m | 2.5 | 2.5 | five |
| mallard | 50 | 40 cm | 9 | 3.6 | 3.8 |
| sparrow | 46 | 12 cm | 13 | 1.6 | eight |
It can be seen that the swift is rightfully considered the best flyer, but the hummingbird does not use energy efficiently, however, this bird does not have the task to fly for a long time, like a pigeon. The identical absolute speeds of the crane, sparrow and duck differ significantly when converted to dimensionless quantities. This kind of calculations are used to simulate a real big plane, testing a small model in a wind tunnel. If all the dimensionless parameters of these two systems are close, they can be considered physically similar and modeling makes sense. We have already used this approach, reflecting relative units instead of absolute ones in the Lorentz diagrams. This allowed us to compare different phenomena and distributions.
It is clear what will be the most suitable system of units in the analysis of the flight of a sandwich. Of course, the length should be measured in sandwiches. Per unit of time you can take the value

In the original formulation, we went through different sizes and obtained a cloud of results, in which the dependence of interest was hidden. With the increase in the number of tests, we averaged this cloud and received an uninteresting answer. To show more clearly what the methodological mistake was, imagine that we want to calculate the probability of the butter falling down, turning randomly both the initial conditions and the size of the sandwich and the height. This is equivalent to averaging all the results we obtained at once. As a result, we will get a confident middle point - the probability is very close to
The cleared data now clearly speak in favor of the law of meanness, limiting it, however, to a certain range of heights: from
And what if you look further and throw sandwiches out of the window? It is clear that when falling from a great height, it doesn’t matter which side fell what turned into a sandwich, and air resistance stabilizes the fall, but theoretically, what do we expect to see? Probably, some fluctuations of probability should be observed with increasing flight time. Let's get a look:

We guessed with frequency, but it is curious that the amplitude decreases, and the fluctuations of probability converge to
Some more dimensional analysis
No matter how frivolous the topic of our book is, we speak the language of mathematics, and he is striving for exact solutions. The Monte Carlo method allowed us to get an idea of the solution, but this was what is called brute force. It is not as interesting as any analytical solution. Dimension analysis will allow us to obtain the theoretical form of the dependence obtained by the Monte Carlo method. To do this, we do not need to solve differential equations, moreover, all our reasoning does not go beyond the limits of quite primitive and obvious relations. This is the charm of dimensional analysis, which, incidentally, sometimes looks like fiction. So let's start, limiting for simplicity just sliding the length of the sandwich
1. The angle of rotation of the falling sandwich depends on the time and angular velocity:
2. The angular velocity equal to the product of the time of sliding and angular acceleration:
3. The creeping time can be expressed in terms of the acceleration of free fall and part of the length of the sandwich, which was in contact with the table with the following proportion:
4. Angular acceleration comes from the acceleration of gravity and depends on the shoulder, to which the force of gravity is attached:
5. Finally, the fall time depends on the height of the table and the acceleration of gravity:
6. Substituting all these expressions in the first formula, we get a simple result:
Which side the sandwich drops is determined by the sign of the sine of the angle
The next task is to express mathematically that the initial positions

The solution we gave before contains more random parameters, so it turned out to be more smooth and close to
Note that the probability
Is it possible to find out without direct calculations, whether the probability will continue to converge to
The great Enrico Fermi, the grandfather of the Monte Carlo method (the father is considered a mathematician Stanislav Ulam), taught his students to do simple evaluative calculations, to estimate on a piece of paper or on fingers, what we expect to get before starting to solve the problem exactly. It is great that if the assessment turns out to be true, it will become clear that the essence of the problem is captured, but if not, then this is all the more useful result - it means that the task turned out to be more interesting than it seems!
In our case, a simple assessment is quite enough; the problem of a sandwich is not worth a more thorough solution. The Monte-Carlo method showed us only a hint of the solution, and the dimension analysis showed only some of its general structure, but together they could show us how the required probability is arranged. Erudition allows mathematics to see ready-made structures in the solutions and make far-reaching assumptions and conclusions.
Robert Matthews, in his landmark study, also used dimensional analysis to show that the law of the sandwich is fundamental. His conclusion is based on the fact that the limiting height of an organism that has risen to the hind limbs with the goal of the forelimbs is to take a sandwich with butter is determined by the strength properties of biological tissues and gravity. In turn, the characteristic size of a sandwich should be consistent with the scale of the creature - and dwarfs on some heavy planet and little dalds on a planet with low gravity will choose their sandwiches in size. Here we come to what in science is called speculation. This is not a resale of any good at exorbitant prices, but dubious assumptions that form the basis of a logical construction. In particular, we assume creatures have hands that have proportions similar to ours, and this is more than debatable.
About oil and wind
In merphology, there is a well-known quotation of the law X.L. Menkina Group:
Difficult problems always have simple, easy to understand wrong decisions.It is very often heard that the law of the sandwich is to blame butter, which is denser than bread and therefore “outweighs”. And although this does not apply to the subject of our book, I want to make out this question in order to put in it, finally, a full stop. So that anyone could then refer to the fact that "scientists have proved that the presence of butter does not affect which side the sandwich splash!"
As children we were amused by throwing high up the pigeon wing feather or tail feather, stuck in a piece of clay, a centimeter or two in diameter. It flew four meters, and then beautifully and smoothly descended to autorotation, like a helicopter with a muffled engine. Then we grew up, and our fun became less harmless. We got a nut and screwed in two bolts from opposite sides, pressing the stuffing from the stitched match heads. It was necessary to tie a ribbon or just a piece of rope to one of the bolts, properly unwind and launch into the sky about fifteen meters. In the fall, the lightweight tape stabilized the vertical position of the projectile, providing a quality impact on the asphalt and a small explosion, sometimes tearing the nut to pieces. (Be careful if you decide to share this childhood experience with your children!)
In both experiments, we see that a light feather or ribbon quickly turned out to be over the hard part of the apparatus and stabilized the fall. This, apparently, leads to the intuitive opinion that heavy butter and light bread should also behave in this way. Imagine a balloon: a denser basket is always located below a dense balloon. Moreover, experience suggests that if you take two fingers to the geometric center of an object with an asymmetrically distributed mass, it will tumble so that the heavy part is at the bottom.
But both of these phenomena do not work in the case of a falling sandwich.
Let's start with the second process - with “outweighing”. It was not by chance that I said boringly: "... if you take up the geometricthe middle of the object .. ", it is meant here that the touch points lie on a certain straight line forming the axis of rotation passing through the center of gravity of the object. In this case, the stable position will be such that the center of gravity is lower than the axis. But if formed by the fingers, the axis of rotation passes through the center of gravity, the system will be in indifferent balance - it will not care how it is oriented.
What makes a feather-weir, a bomb made of a nut, or a balloon with aeronauts in a basket make you orientate in the “right” way? Air. It “holds” our objects so that the axis passes above the center of gravity. More precisely, the oncoming flow of air, creating a force distributed over the area of the body. And the conditional point of application of this force will be located near the geometric center of the area of the figure. To make it clearer, let's draw the forces acting on a conditional balloon as an object with an uneven density:

And what's a sandwich?
First, if we “turn off” the air, it will just fall. In free fall, the body rotates precisely around the center of mass, so that it has no reason to turn in any particular way. As they say in school: "Weightlessness is observed in a falling elevator." The butter on the sandwich is just as "weightless."
Dense oil can affect the process of slipping, it will effectively raise the center of mass above the exact touch and change in the expression for the angular acceleration
Now "turn on" the air back, leaving the density of butter infinitely greater than the density of bread. We have a thin dense plate with a weightless, but air-resisting “parachute”. As long as the sandwich plane is horizontal or so, a moment of air resistance forces acts on it proportional to the sail area — the area with which the air flow interacts:
 We could use the work of the resistance forces as a measure and would get the same ratio. The angle ratio is easy to calculate:
We could use the work of the resistance forces as a measure and would get the same ratio. The angle ratio is easy to calculate:If it seemed to the reader that we were now firing from a cannon on sparrows, then I completely agree with him. But, firstly, I don’t want to hear more about the “outweighing” oil, secondly, I don’t want to be unfounded, and thirdly, I wanted to show how the physicist assesses values, representing the process, but not having complete data. Of course, at the moment of landing, the oil can stick to the floor and prevent the sandwich from jumping up and rolling over again, but I certainly will not disassemble the mechanics of the impact, elastic deformation and jump of a piece of bread. So there was a bit of analysis for this problem. And the second Nobel for her will not give.
The goal of our path was not so important: a refutation or justification of the law of a sandwich, as the path itself. He showed how the combination of different mathematical methods allows us to look at the problem from different angles and gives a fairly accurate knowledge, even without a detailed solution of the problem. In the consistency of various mathematical disciplines, approaches and points of view is the strength and beauty of mathematics. It is appropriate to recall the wonderful words of Marina Tsvetaeva: “I don’t want to have a point of view, I want to have a sight” . The study of various areas of mathematics is able to give the researcher a real “three-dimensional” multidimensional vision, which allows you to look into the seemingly closed and hidden space of knowledge.
