Last time, we looked at the PostgreSQL indexing mechanism , the access method interface , and two methods: a hash index and a B-tree . In this part, we will deal with the GiST indices.

Gist

GiST stands for generalized search tree. This is a balanced search tree, just like the b-tree discussed earlier.

What is the difference? The b-tree index is tightly tied to the semantics of comparison: support for the operators "more", "less", "equal" is all that it is capable of (but it is capable of very well!). But modern types of data are also stored in modern databases for which these operators simply do not make sense: geodata, text documents, pictures ...

Here the GiST index method comes to the rescue. It allows you to specify the principle of distributing data of an arbitrary type in a balanced tree, and the method of using this view to access some operator. For example, in the GiST index, you can “stack” an R-tree for spatial data with support for relative positioning operators (located on the left, right; contains, etc.), or an RD-tree for sets with support for intersection or entry operators.

Due to extensibility in PostgreSQL, it’s quite possible to create a completely new access method from scratch: for this you need to implement an interface with an indexing mechanism. But this requires thinking through not only the logic of indexing, but also the page structure, the effective implementation of locks, support for the write-ahead log - which implies a very high qualification of the developer and great laboriousness. GiST simplifies the task by taking on low-level problems and providing its own interface: several functions related not to the technical field, but to the application area. In this sense, we can say that GiST is a framework for building new access methods.

Device

GiST is a height-balanced tree consisting of page nodes. Nodes are made up of index entries.

Each record of a leaf node (leaf record) contains, in the most general form, a predicate (logical expression) and a link to a table row (TID). Indexed data (key) must satisfy this predicate.

Each record of the internal node (internal record) also contains a predicate and a link to a child node, and all indexed data of the child subtree must satisfy this predicate. In other words, the predicate of the internal record includes the predicates of all child records. This is an important property that replaces the GiST index with simple B-tree ordering.

A search in the GiST tree uses a special function of consistency (consistent) - one of the functions defined by the interface, and implemented in its own way for each supported family of operators.

The consistency function is called for the index record and determines whether the predicate of the record is “consistent” with the search condition (of the form “ indexed-field operator expression ”). For an internal record, it actually determines whether it is necessary to go down to the corresponding subtree, and for a sheet record, whether the indexed data satisfies the condition.

A search, as usual in a tree, starts from the root node. Using the consistency function, it is found out which child nodes it makes sense to go into (there may be several), and which ones do not. Then the algorithm is repeated for each of the found child nodes. If the node is a leaf node, then the record selected by the consistency function is returned as one of the results.

The search is performed in depth: the algorithm first of all tries to get to some leaf node. This allows you to quickly return the first results as soon as possible (which may be important if the user is not interested in all the results, but only a few).

Once again, we note that the consistency function should not have any relation to the operators “more”, “less” or “equal”. Its semantics can be completely different, and therefore it is not assumed that the index will produce values ​​in any particular order.

We will not consider algorithms for inserting and deleting values ​​in GiST - for this, several more interface functions are used. But there is one important point. When a new value is inserted into the index, a parent record is selected for it so that its predicate should be expanded as little as possible (ideally, not expanded at all). But when the value is deleted, the predicate of the parent record no longer narrows. This happens only in two cases: when the page is divided into two (when the page does not have enough space to insert a new index record) and when the index is completely rebuilt (with reindex or vacuum full commands). Therefore, the effectiveness of the GiST index with frequently changing data can degrade over time.

Further we will consider some examples of indexes for different data types and useful properties of GiST:

• points (and other geometric objects) and the search for nearest neighbors;
• intervals and exclusion restrictions;
• full text search.

R-tree for points

Let us demonstrate what was said above using an example of an index for points on a plane (similar indices can also be constructed for other geometric objects). A regular B-tree is not suitable for this type of data, since comparison operators are not defined for points.

The idea of ​​an R-tree is that the plane is divided into rectangles, which in total cover all indexed points. The index record stores the rectangle, and the predicate can be formulated as follows: "the desired point lies inside the given rectangle."

The root of the R-tree will contain some of the largest rectangles (possibly even intersecting). The child nodes will contain smaller rectangles nested in the parent, together covering all the underlying points.

Leaf nodes, in theory, should contain indexable points, however, the data type in all index records should match; therefore, all the same rectangles are stored, but “collapsed” to the points.

To visualize such a structure, below are the figures of the three levels of the R-tree; the points represent the coordinates of the airports (similar to the airports table of the demo base, but more data from openflights.org is taken here ).


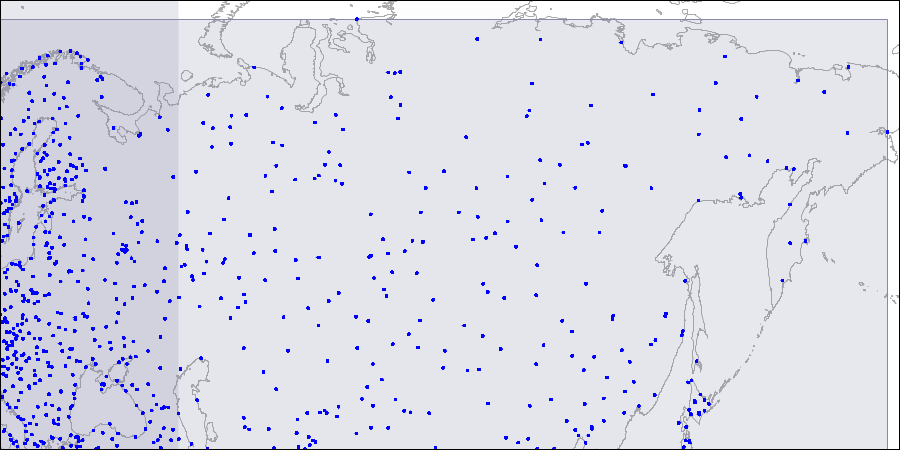
First level; two large intersecting rectangles are visible.


Second level; large rectangles break up into smaller areas.


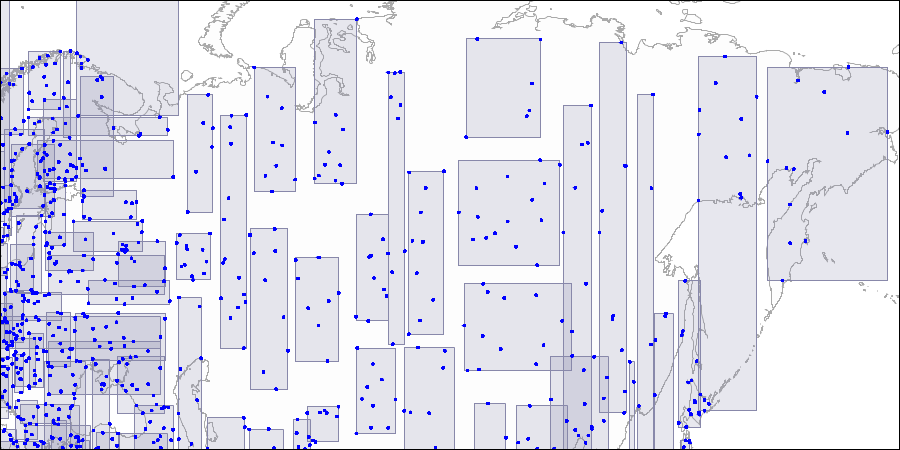
Third level; each rectangle contains so many points to fit on one index page.

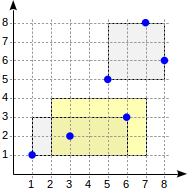
Now let's take a closer look at a very simple “single-level” example:



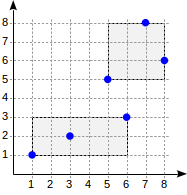
postgres=# create table points(p point);
CREATE TABLE
postgres=# insert into points(p) values
  (point '(1,1)'), (point '(3,2)'), (point '(6,3)'),
  (point '(5,5)'), (point '(7,8)'), (point '(8,6)');
INSERT 0 6
postgres=# create index on points using gist(p);
CREATE INDEX

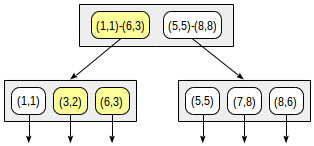
The structure of the index with such a partition will look like this:



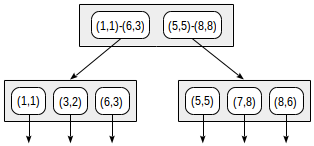
The created index can be used to speed up, for example, such a query: "find all points that are in the given rectangle." This condition is formulated as follows: p <@ box '(2,1),(6,3)'(an operator <@from the points_ops family means "contained in"): The consistency function for such an operator (" indexed field <@ expression ", where indexed field is a point and expression  is a rectangle) is defined as follows. For an internal record, it returns “yes” if its rectangle intersects with the rectangle defined by the expression.

postgres=# set enable_seqscan = off;
SET
postgres=# explain(costs off) select * from points where p <@ box '(2,1),(7,4)';
                  QUERY PLAN                  
----------------------------------------------
 Index Only Scan using points_p_idx on points
   Index Cond: (p <@ '(7,4),(2,1)'::box)
(2 rows)

For a sheet record, the function returns “yes” if its point (“collapsed” rectangle) is contained in the rectangle defined by the expression.



The search begins at the root node. The rectangle (2,1) - (7,4) intersects with (1,1) - (6,3), but does not intersect with (5,5) - (8,8), so there is no need to go down to the second subtree.



Arriving at the leaf node, we sort out the three points contained there and return two of them as a result: (3,2) and (6,3).

postgres=# select * from points where p <@ box '(2,1),(7,4)';
   p  
-------
 (3,2)
 (6,3)
(2 rows)


Inside

The usual pageinspect, alas, does not allow you to look inside the GiST index. But there is another way - gevel extension. It is not included in the standard delivery; See installation instructions .

If everything is done correctly, three functions will be available to you. Firstly, some statistics: Here you can see that the airport coordinates index took 690 pages and consists of four levels: the root and two internal levels were shown above in the figures, and the fourth level was sheet. In fact, the index for eight thousand points will occupy much less space: here, for clarity, it was created with a filling of 10%. Secondly, you can display the index tree:

postgres=# select * from gist_stat('airports_coordinates_idx');
                gist_stat                
------------------------------------------
 Number of levels:          4            +
 Number of pages:           690          +
 Number of leaf pages:      625          +
 Number of tuples:          7873         +
 Number of invalid tuples:  0            +
 Number of leaf tuples:     7184         +
 Total size of tuples:      354692 bytes +
 Total size of leaf tuples: 323596 bytes +
 Total size of index:       5652480 bytes+
 
(1 row)







postgres=# select * from gist_tree('airports_coordinates_idx');
                                       gist_tree                                              
-----------------------------------------------------------------------------------------
 0(l:0) blk: 0 numTuple: 5 free: 7928b(2.84%) rightlink:4294967295 (InvalidBlockNumber) +
     1(l:1) blk: 335 numTuple: 15 free: 7488b(8.24%) rightlink:220 (OK)                 +
         1(l:2) blk: 128 numTuple: 9 free: 7752b(5.00%) rightlink:49 (OK)               +
             1(l:3) blk: 57 numTuple: 12 free: 7620b(6.62%) rightlink:35 (OK)           +
             2(l:3) blk: 62 numTuple: 9 free: 7752b(5.00%) rightlink:57 (OK)            +
             3(l:3) blk: 72 numTuple: 7 free: 7840b(3.92%) rightlink:23 (OK)            +
             4(l:3) blk: 115 numTuple: 17 free: 7400b(9.31%) rightlink:33 (OK)          +
 ...

And thirdly, you can display the data itself, which is stored in index entries. Thin point: the result of the function must be converted to the desired data type. In our case, this type is box (bounding box). For example, at the top level we see five records: Actually, the figures above were prepared just on the basis of these data.

postgres=# select level, a from gist_print('airports_coordinates_idx')
  as t(level int, valid bool, a box) where level = 1;
 level |                                   a                                  
-------+-----------------------------------------------------------------------
     1 | (47.663586,80.803207),(-39.2938003540039,-90)
     1 | (179.951004028,15.6700000762939),(15.2428998947144,-77.9634017944336)
     1 | (177.740997314453,73.5178070068359),(15.0664,10.57970047)
     1 | (-77.3191986083984,79.9946975708),(-179.876998901,-43.810001373291)
     1 | (-39.864200592041,82.5177993774),(-81.254096984863,-64.2382965088)
(5 rows)


Search and collation operators

The operators considered so far (such as <@in the predicate p <@ box '(2,1),(7,4)'), can be called search ones, since they specify the search conditions in the query.

There are another type of operators - ordering ones. They are used to indicate the order of the results to be returned in the order by phrase where it is usually used a simple indication of the fields Here is an example of such a query: Here  is an expression using an ordering operator that indicates the distance from one argument to another.The meaning of the query is to return two points closest to the point (4.7). Such a search is known as k-NN - k-nearest neighbor search. To support this type of query, the access method must define an additional distance function

postgres=# select * from points order by p <-> point '(4,7)' limit 2;
   p  
-------
 (5,5)
 (7,8)
(2 rows)


p <-> point '(4,7)'<->

(distance), and the ordering operator must be included in the corresponding class of operators (for example, for points, the points_ops class). Here is a query that shows the operators and their type (s - search, o - ordering): Here are also shown the numbers of strategies with a breakdown of their value. It can be seen that there are much more strategies than btree; only part of them is supported for points. For other data types, other strategies may be defined. The distance function is called for the index element and must determine the distance (taking into account the semantics of the operator) from the value determined by the expression (" indexed-field ordering-operator expression

postgres=# select amop.amopopr::regoperator, amop.amoppurpose, amop.amopstrategy
from pg_opclass opc, pg_opfamily opf, pg_am am, pg_amop amop
where opc.opcname = 'point_ops'
and opf.oid = opc.opcfamily
and am.oid = opf.opfmethod
and amop.amopfamily = opc.opcfamily
and am.amname = 'gist'
and amop.amoplefttype = opc.opcintype;
      amopopr      | amoppurpose | amopstrategy
-------------------+-------------+--------------
 <<(point,point)   | s           |            1  строго слева
 >>(point,point)   | s           |            5  строго справа
 ~=(point,point)   | s           |            6  совпадает
 <^(point,point)   | s           |           10  строго снизу
 >^(point,point)   | s           |           11  строго сверху
 <->(point,point)  | o           |           15  расстояние
 <@(point,box)     | s           |           28  содержится в прямоугольнике
 <@(point,polygon) | s           |           48  содержится в полигоне
 <@(point,circle)  | s           |           68  содержится в окружности
(9 rows)



"), Up to this element. For a leaf element, this is simply the distance to the indexed value. For an internal element, the function should return the minimum of the distances to the child leaf elements. Since it would be very expensive to sort through all child records, the function has the right to optimistically reduce the distance, but at the cost of deteriorating search efficiency. However, it should not be exaggerated categorically - this will disrupt the index.

The distance function can return a value of any type that allows sorting (PostgreSQL will use the comparison semantics from the corresponding family of btree accessor method operators for ordering, as described earlier ).

In the case of points on a plane, distance is understood in the most ordinary sense: the meaning of the expression(x1,y1) <-> (x2,y2)equal to the root of the sum of the squares of the differences of abscissas and ordinates. The distance from a point to a bounding rectangle is the minimum distance from a point to this rectangle, or zero if the point is inside it. This value is easy to calculate without going around the child points, and it is guaranteed no more than the distance to any of the child points.

Consider the search algorithm for the above query.



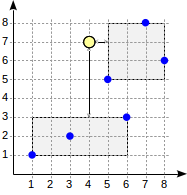
The search begins at the root node. It has two bounding boxes. The distance to (1.1) - (6.3) is 4.0, and to (5.5) - (8.8) is 1.0.

Child nodes are crawled in order of increasing distance. Thus, we first go down to the nearest child node and find the distances to the points (for clarity, we will show the numbers in the figure):



This information is already enough to return the first two points (5.5) and (7.8). Since we know that the distance to the points inside the rectangle (1,1) - (6,3) is 4.0 or more, there is no need to go down to the first child node.

What if we needed to find the first three points? Although all these points are contained in the second child node, we cannot return (8.6) without looking at the first child node, since there may be closer points (since 4.0 <4.1). This example explains the requirements for the distance function for internal records. Choosing a shorter distance for the second record (4.0 instead of real 4.5), we worsened the efficiency (the algorithm began to look at the extra node in vain), but did not violate the correct operation.

postgres=# select * from points order by p <-> point '(4,7)' limit 3;
   p  
-------
 (5,5)
 (7,8)
 (8,6)
(3 rows)








Until recently, GiST was the only access method that could work with collating operators. But the situation has changed: the RUM method has already been added to this company (which we will talk about later), and it is possible that they will be joined by the good old B-tree - a patch written by our colleague Nikita Glukhov is being discussed by the community.

R-tree for intervals

Another example of using the gist access method is indexing intervals, for example, time intervals (type tsrange). The whole difference is that the internal nodes of the tree will contain not bounding rectangles, but bounding intervals.

A simple example. We will rent a house in the village and store the booking intervals in the table: The index can be used, for example, to speed up the following request: The operator for the intervals indicates the intersection; thus, the request should return all intervals that intersect with the given one. For such an operator, the consistency function determines whether the specified interval intersects with the value in the internal or leaf record.

postgres=# create table reservations(during tsrange);
CREATE TABLE
postgres=# insert into reservations(during) values
('[2016-12-30, 2017-01-09)'),
('[2017-02-23, 2017-02-27)'),
('[2017-04-29, 2017-05-02)');
INSERT 0 3
postgres=# create index on reservations using gist(during);
CREATE INDEX



postgres=# select * from reservations where during && '[2017-01-01, 2017-04-01)';
                    during                    
-----------------------------------------------
 ["2016-12-30 00:00:00","2017-01-08 00:00:00")
 ["2017-02-23 00:00:00","2017-02-26 00:00:00")
(2 rows)

postgres=# explain (costs off) select * from reservations where during && '[2017-01-01, 2017-04-01)';
                                     QUERY PLAN                                    
------------------------------------------------------------------------------------
 Index Only Scan using reservations_during_idx on reservations
   Index Cond: (during && '["2017-01-01 00:00:00","2017-04-01 00:00:00")'::tsrange)
(2 rows)

&&

Note that in this case, we are not talking about how to obtain intervals in a certain order, although comparison operators are defined for intervals. You can use the b-tree index for them, but in this case you will have to do without supporting operations such as: (In addition to the equality, which is also part of the operator class for the btree access method.)

postgres=# select amop.amopopr::regoperator, amop.amoppurpose, amop.amopstrategy
from pg_opclass opc, pg_opfamily opf, pg_am am, pg_amop amop
where opc.opcname = 'range_ops'
and opf.oid = opc.opcfamily
and am.oid = opf.opfmethod
and amop.amopfamily = opc.opcfamily
and am.amname = 'gist'
and amop.amoplefttype = opc.opcintype;
         amopopr         | amoppurpose | amopstrategy
-------------------------+-------------+--------------
 @>(anyrange,anyelement) | s           |           16  содержит элемент
 <<(anyrange,anyrange)   | s           |            1  строго слева
 &<(anyrange,anyrange)   | s           |            2  не выходит за правую границу
 &&(anyrange,anyrange)   | s           |            3  пересекается
 &>(anyrange,anyrange)   | s           |            4  не выходит за левую границу
 >>(anyrange,anyrange)   | s           |            5  строго справа
 -|-(anyrange,anyrange)  | s           |            6  прилегает
 @>(anyrange,anyrange)   | s           |            7  содержит интервал
 <@(anyrange,anyrange)   | s           |            8  содержится в интервале
 =(anyrange,anyrange)    | s           |           18  равен
(10 rows)


Inside

You can peek inside with the same gevel extension. Just remember to change the data type in the gist_print call:

postgres=# select level, a from gist_print('reservations_during_idx')
as t(level int, valid bool, a tsrange);
 level |                       a                      
-------+-----------------------------------------------
     1 | ["2016-12-30 00:00:00","2017-01-09 00:00:00")
     1 | ["2017-02-23 00:00:00","2017-02-27 00:00:00")
     1 | ["2017-04-29 00:00:00","2017-05-02 00:00:00")
(3 rows)


Exclusion limit

The GiST index can be used to support exclude constraints.

The exclusion restriction ensures that the specified fields of any two rows of the table will not "match" each other in the sense of some operator. If “equal” is chosen as the operator, then an uniqueness constraint is exactly obtained: the specified fields of any two lines are not equal to each other.

Like the uniqueness constraint, the exception constraint is supported by the index. You can select any operator, if only he:

1. supported by the index method - the can_exclude property (for example, the btree, gist or spgist methods, but not the gin methods);
2. was commutative, that is, the condition must be satisfied: a operator b =
   b operator a.

Here is a list of suitable strategies and examples of operators (operators, as we recall, may be called differently and may not be available for all data types):

• for btree:
  
  • "equally" =
  
  
• for gist and spgist:
  
  • "Intersection" &&
  • "coincidence" ~=
  • "Fit" -|-
  
  

Note that it is possible to use the equality operator in the restriction of exclusion, but it does not make practical sense: the restriction of uniqueness will be more efficient. That is why we did not address exclusion restrictions when we talked about B-trees.

Here is an example of using an exception constraint. It is logical not to allow the reservation of the house at intersecting time intervals. After creating an integrity constraint, we can add rows: But trying to insert an intersecting interval in the table will result in an error:

postgres=# alter table reservations add exclude using gist(during with &&);
ALTER TABLE



postgres=# insert into reservations(during) values ('[2017-06-10, 2017-06-13)');
INSERT 0 1



postgres=# insert into reservations(during) values ('[2017-05-15, 2017-06-15)');
ERROR: conflicting key value violates exclusion constraint "reservations_during_excl"
DETAIL: Key (during)=(["2017-05-15 00:00:00","2017-06-15 00:00:00")) conflicts with existing key (during)=(["2017-06-10 00:00:00","2017-06-13 00:00:00")).


Btree_gist extension

Let's complicate the task. Our modest business is expanding and we are going to rent out several houses: We need to change the exclusion restriction so as to take into account the house number. However, GiST does not support the equality operation for integers: In this case, the btree_gist extension will help , which adds GiST support for operations specific to B-trees. In the end, GiST can work with any operator, so why not teach it to work with "more", "less", "equal"? Now we still cannot book the first house on the same dates: But we can book the second:

postgres=# alter table reservations add house_no integer default 1;
ALTER TABLE



postgres=# alter table reservations drop constraint reservations_during_excl;
ALTER TABLE
postgres=# alter table reservations add exclude using gist(during with &&, house_no with =);
ERROR: data type integer has no default operator class for access method "gist"
HINT: You must specify an operator class for the index or define a default operator class for the data type.



postgres=# create extension btree_gist;
CREATE EXTENSION
postgres=# alter table reservations add exclude using gist(during with &&, house_no with =);
ALTER TABLE



postgres=# insert into reservations(during, house_no) values ('[2017-05-15, 2017-06-15)', 1);
ERROR: conflicting key value violates exclusion constraint "reservations_during_house_no_excl"



postgres=# insert into reservations(during, house_no) values ('[2017-05-15, 2017-06-15)', 2);
INSERT 0 1

But you need to understand that although GiST can somehow work with the operations “more”, “less”, “equal”, the B-tree still copes with them better. So this technique should be used only if the GiST index is essentially necessary - as in our example.

Full-text RD tree

About full-text search

Let's start with a minimalist introduction to PostgreSQL full-text search (if you're in the topic, you can safely skip this section).

The task of full-text search is to select those that match the search query from a set of documents . (If there are a lot of results, it is important to find the best match, but keep silent about it.) The document is converted to a special type tsvector for search purposes, which contains tokens and their positions in the document. Tokens are words that are converted to a form that is convenient for searching. For example, by default, words are reduced to lowercase and their variable endings are cut off:



postgres=# set default_text_search_config = russian;
SET
postgres=# select to_tsvector('И встал Айболит, побежал Айболит. По полям, по лесам, по лугам он бежит.');
                            to_tsvector                            
--------------------------------------------------------------------
 'айбол':3,5 'беж':13 'встал':2 'лес':9 'луг':11 'побежа':4 'пол':7
(1 row)

It is also seen here that some words (called stop words ) are generally ejected (“and”, “by”), as they are supposedly found too often to make a meaningful search. Of course, all these transformations are customizable, but this is not about that.

The search query is represented by another type - tsquery. A query, roughly speaking, consists of one or more tokens connected by logical connectives: “and” &, “or” |, “not” !. You can also use parentheses to specify the priority of operations. For full-text search, a single @@ match operator is used. This information will be enough for now. Let's talk a bit more about full-text search in one of the following sections on the GIN index.

postgres=# select to_tsquery('Айболит & (побежал | пошел)');
            to_tsquery            
----------------------------------
 'айбол' & ( 'побежа' | 'пошел' )
(1 row)



postgres=# select to_tsvector('И встал Айболит, побежал Айболит.') @@ to_tsquery('Айболит & (побежал | пошел)');
 ?column?
----------
 t
(1 row)

postgres=# select to_tsvector('И встал Айболит, побежал Айболит.') @@ to_tsquery('Бармалей & (побежал | пошел)');
 ?column?
----------
 f
(1 row)


RD trees

In order for full-text search to work quickly, you need, firstly, to store a column of the tsvector type in the table (so as not to perform an expensive conversion each time you search), and secondly, build an index on this field. One of the possible access methods for this is GiST. The last step (converting the document to tsvector), of course, is conveniently assigned to the trigger. How should the index be arranged? The R-tree itself is not suitable here - it is not clear what the “bounding box” is for documents. But you can apply some modification of this approach for sets - the so-called RD-tree (RD is a Russian Doll, a nested doll). By a plurality in this case we mean a lot of document tokens, but in general a plurality can be any.

postgres=# create table ts(doc text, doc_tsv tsvector);
CREATE TABLE
postgres=# create index on ts using gist(doc_tsv);
CREATE INDEX
postgres=# insert into ts(doc) values
  ('Во поле береза стояла'),  ('Во поле кудрявая стояла'), ('Люли, люли, стояла'),
  ('Некому березу заломати'), ('Некому кудряву заломати'), ('Люли, люли, заломати'),
  ('Я пойду погуляю'),        ('Белую березу заломаю'),    ('Люли, люли, заломаю');
INSERT 0 9
postgres=# update ts set doc_tsv = to_tsvector(doc);
UPDATE 9



postgres=# select * from ts;
           doc           |            doc_tsv            
-------------------------+--------------------------------
 Во поле береза стояла   | 'берез':3 'пол':2 'стоя':4
 Во поле кудрявая стояла | 'кудряв':3 'пол':2 'стоя':4
 Люли, люли, стояла      | 'люл':1,2 'стоя':3
 Некому березу заломати  | 'берез':2 'заломат':3 'нек':1
 Некому кудряву заломати | 'заломат':3 'кудряв':2 'нек':1
 Люли, люли, заломати    | 'заломат':3 'люл':1,2
 Я пойду погуляю         | 'погуля':3 'пойд':2
 Белую березу заломаю    | 'бел':1 'берез':2 'залома':3
 Люли, люли, заломаю     | 'залома':3 'люл':1,2
(9 rows)



The idea of ​​RD-trees is to take a bounding set instead of a bounding box - that is, a set containing all elements of child sets.

An important question is how to represent sets in index records. Probably the most straightforward way is to simply list all the elements of the set. Here's what it might look like:



Then, for example, for access by condition, doc_tsv @@ to_tsquery('стояла')you could lower it only to those nodes that have a standing token:



The problems with this view are quite obvious. The number of tokens in a document can be quite large, so index entries will take up a lot of space and end up in TOAST, making the index much less efficient. Even if there are a few unique tokens in each document, the union of sets can still turn out to be very large - the higher the root, the more index entries there will be.

This representation is sometimes used, but for other data types. And for a full-text search, another, more compact solution is used - the so-called signature tree. His idea is well known to everyone who dealt with the Bloom filter.

Each token can be represented by its signature:a bit string of a certain length in which all bits are zero except one. The number of this bit is determined by the value of the hash function of the token (we talked about how the hash functions are arranged earlier ).

A document signature is a bitwise “or” signature of all document tokens.

Suppose the signatures of our tokens are as follows: Then the signatures of the documents are as follows: The index tree can be represented as follows: The advantages of this approach are obvious: index records are the same and small in size, the index is compact. But a drawback is also visible: accuracy is lost due to compactness. Consider the same condition

бел      1000000
берез    0001000
залома   0000010
заломат  0010000
кудряв   0000100
люл      0100000
нек      0000100
погуля   0000001
пойд     0000010
пол      0000010
стоя     0010000



Во поле береза стояла     0011010
Во поле кудрявая стояла   0010110
Люли, люли, стояла        0110000
Некому березу заломати    0011100
Некому кудряву заломати   0010100
Люли, люли, заломати      0110000
Я пойду погуляю           0000011
Белую березу заломаю      1001010
Люли, люли, заломаю       0100010








doc_tsv @@ to_tsquery('стояла'). We calculate the signature of the search query in the same way as for the document: in our case 0010000. The consistency function should return all the child nodes whose signature contains at least one bit from the query signature:



Compare with the picture above: it is clear that the tree is “yellowed” - and this means that false positives occur (what we call errors of the first kind) and extra nodes are searched for during the search. Here we hooked the “zalomat” token, the signature of which unfortunately coincided with the signature of the desired “token” token. It is important that there can be no false negative responses (errors of the second kind) in such a scheme, that is, we are guaranteed not to miss the desired value.

In addition, it may happen that different documents receive the same signatures: in our example, “luli, luli, stood” and “luli, luli, creased” were unlucky (both have 0110000 signature). And if the tsvector value itself is not stored in the sheet index entry, then the index itself will give false positives. Of course, in this case, the access method will ask the index mechanism to double-check the result against the table, so that the user will not see these false positives. But search performance may well be affected.

In fact, the signature in the current implementation takes 124 bytes instead of seven bits in our pictures, so the probability of collisions is significantly less than in the example. But after all, in practice, much more documents are indexed. To somehow reduce the number of false positives of the index method, the implementation is tricked: the indexed tsvector is stored in a sheet index record, but only if it does not take up much space (a little less than 1/16 of a page, which is about half a kilobyte for 8 KB pages) .

Example

To see how indexing works on real data, take the pgsql-hackers mailing list. The version used in the example contains 356125 letters with the date of departure, subject, author and text: Add and fill in a column of type tsvector and build an index. Here we combine three values ​​into one vector (subject, author and letter text) to show that the document does not have to be a single field, but can consist of completely arbitrary parts. A certain number of words, as can be seen, were discarded due to too large a size. But in the end, the index is built and ready to support search queries:

fts=# select * from mail_messages order by sent limit 1;
-[ RECORD 1 ]------------------------------------------------------------------------
id         | 1572389
parent_id  | 1562808
sent       | 1997-06-24 11:31:09
subject    | Re: [HACKERS] Array bug is still there....
author     | "Thomas G. Lockhart"
body_plain | Andrew Martin wrote:                                                    +
           | > Just run the regression tests on 6.1 and as I suspected the array bug +
           | > is still there. The regression test passes because the expected output+
           | > has been fixed to the *wrong* output.                                 +
           |                                                                         +
           | OK, I think I understand the current array behavior, which is apparently+
           | different than the behavior for v1.0x.                                  +
             ...



fts=# alter table mail_messages add column tsv tsvector;
ALTER TABLE
fts=# update mail_messages
set tsv = to_tsvector(subject||' '||author||' '||body_plain);
NOTICE:  word is too long to be indexed
DETAIL:  Words longer than 2047 characters are ignored.
...
UPDATE 356125
fts=# create index on mail_messages using gist(tsv);
CREATE INDEX



fts=# explain (analyze, costs off)
select * from mail_messages where tsv @@ to_tsquery('magic & value');
                        QUERY PLAN
----------------------------------------------------------
 Index Scan using mail_messages_tsv_idx on mail_messages
 (actual time=0.998..416.335 rows=898 loops=1)
   Index Cond: (tsv @@ to_tsquery('magic & value'::text))
   Rows Removed by Index Recheck: 7859
 Planning time: 0.203 ms
 Execution time: 416.492 ms
(5 rows)

Here you can see that together with 898 rows matching the condition, the access method returned another 7859 rows that were eliminated by double-checking the table. This clearly shows the negative impact of accuracy loss on efficiency.

Inside

To analyze the contents of the index, we again use the gevel extension: Values ​​of a special type gtsvector stored in index records are the signature itself, plus, possibly, the original tsvector. If there is a vector, then the number of tokens in it (unique words) is displayed, and if not, the number of set (true) and reset (false) bits in the signature is displayed. It can be seen that in the root node the signature degenerated to “all units” - that is, one index level became completely useless (and one more - almost completely useless with only four bits reset).

fts=# select level, a from gist_print('mail_messages_tsv_idx') as t(level int, valid bool, a gtsvector) where a is not null;
 level |               a              
-------+-------------------------------
     1 | 992 true bits, 0 false bits
     2 | 988 true bits, 4 false bits
     3 | 573 true bits, 419 false bits
     4 | 65 unique words
     4 | 107 unique words
     4 | 64 unique words
     4 | 42 unique words
...


The properties

Let's take a look at the properties of the gist access method (requests were given earlier ): There is no support for sorting values ​​and uniqueness. An index, as we have seen, can be built on several columns and used in exclusion constraints. Index Properties: And, most interesting, column level properties. Some properties will be permanent: (There is no support for sorting; the index cannot be used to search in an array; undefined values ​​are supported.) But the two remaining properties, distance_orderable and returnable, will depend on the class of operators used. For example, for points we will see:

 amname |     name      | pg_indexam_has_property
--------+---------------+-------------------------
 gist   | can_order     | f
 gist   | can_unique    | f
 gist   | can_multi_col | t
 gist   | can_exclude   | t





     name      | pg_index_has_property
---------------+-----------------------
 clusterable   | t
 index_scan    | t
 bitmap_scan   | t
 backward_scan | f



        name        | pg_index_column_has_property
--------------------+------------------------------
 asc                | f
 desc               | f
 nulls_first        | f
 nulls_last         | f
 orderable          | f
 search_array       | f
 search_nulls       | t





        name        | pg_index_column_has_property
--------------------+------------------------------
 distance_orderable | t
 returnable         | t

The first property indicates that a distance operator is available to search for nearest neighbors. And the second is that the index can be used exclusively in index scanning. Despite the fact that not index points, but rectangles are stored in sheet index records, the access method can return what is needed.

And here are the intervals: The distance function is not defined for them, therefore, the search for the nearest neighbors is impossible. And full-text search:

        name        | pg_index_column_has_property
--------------------+------------------------------
 distance_orderable | f
 returnable         | t





        name        | pg_index_column_has_property
--------------------+------------------------------
 distance_orderable | f
 returnable         | f

Here, the ability to perform an exclusively index scan was lost, since only a signature without data itself can appear in leaf records. However, this is a small loss, since a value of type tsvector still does not interest anyone: it is used to select rows, and you need to show the source text, which is still not in the index.

Other data types

In conclusion, we denote a few more types that the GiST access method currently supports, in addition to the geometric types that we have already examined (using points as examples), ranges, and full-text search types.

Of the standard types, these are inet IP addresses , and the rest is added by extensions:

• cube provides the cube data type for multidimensional cubes. For him, as well as for geometric types on the plane, a class of GiST operators is defined: an R-tree with the ability to search for nearest neighbors.
  
• seg provides the seg data type for intervals with boundaries specified with a certain accuracy, and support for the GiST index for it (R-tree).
  
• intarray extends the functionality of integer arrays and adds GiST support for them. Two classes of operators are implemented: gist__int_ops (RD-tree with full representation of keys in index entries) and gist__bigint_ops (signature RD-tree). The first class can be used for small arrays, the second - for more serious volumes.
  
• ltree adds the ltree data type for tree structures and GiST support for it (RD tree).
  
• pg_trgm adds a special class of gist_trgm_ops operators for using trigrams in full-text search. But more about that - another time along with the GIN index.
  

To be continued .