Keras Auto Encoders, Part 2: Manifold learning and latent variables
- Tutorial
Content
- Part 1: Introduction
- Part 2: Manifold learning and latent variables
- Part 3: Variable Variable Encoders ( VAE )
- Part 4: Conditional VAE
- Part 5: GAN (Generative Adversarial Networks) and tensorflow
- Part 6: VAE + GAN
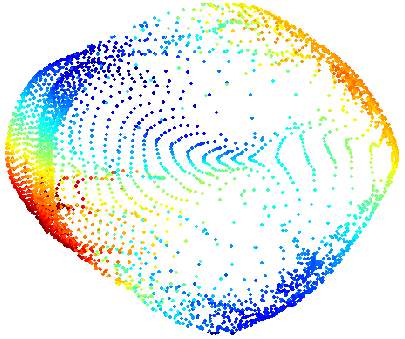
In order to better understand how auto-encoders work, as well as to subsequently generate something new from codes, it’s worth understanding what codes are and how they can be interpreted.
Manifold learning
The images of the mnist numbers (in which the examples in the last part) are elements of
However, among all the images, the images of the numbers occupy only a negligible part, the absolute majority of the images are just noise.
On the other hand, if we take an arbitrary image of a figure, then all the images from a certain neighborhood can also be considered a figure.
And if we take two arbitrary images of a digit, then in the original 784-dimensional space, most likely, you can find a continuous curve, all the points along which can also be considered digits (at least for images of the digits of one label), and together with the previous remark, that's all points of some region along this curve.
Thus, in the space of all images there is some subspace of smaller dimension in the area around which the images of numbers are concentrated. That is, if our general population is all the images of numbers that can be drawn in principle, then the probability density to meet such a figure within the region is much higher than outside.
Auto encoders with a dimension of code k are looking for a k-dimensional manifold in the space of objects that most fully conveys all the variations in the sample. And the code itself sets the parameterization of this variety. In this case, the encoder maps the object to its parameter on the manifold, and the decoder maps the parameter to a point in the space of objects.
The larger the dimension of the codes, the more variations in the data the encoder can transmit. If the dimension of the codes is too small, the auto-encoder will remember something averaged over the missing variations in the given metric (this is one of the reasons why mnist digits are more blurry with decreasing code dimension in auto-encoders).
In order to better understand what manifold learning is , create a simple two-dimensional dataset in the form of a curve plus noise and train the auto-encoder on it.
Code and visualization
# Импорт необходимых библиотек
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
# Создание датасета
x1 = np.linspace(-2.2, 2.2, 1000)
fx = np.sin(x1)
dots = np.vstack([x1, fx]).T
noise = 0.06 * np.random.randn(*dots.shape)
dots += noise
# Цветные точки для отдельной визуализации позже
from itertools import cycle
size = 25
colors = ["r", "g", "c", "y", "m"]
idxs = range(0, x1.shape[0], x1.shape[0]//size)
vx1 = x1[idxs]
vdots = dots[idxs]
# Визуализация
plt.figure(figsize=(12, 10))
plt.xlim([-2.5, 2.5])
plt.scatter(dots[:, 0], dots[:, 1])
plt.plot(x1, fx, color="red", linewidth=4)
plt.grid(False)

In the picture above: the blue dots are the data, and the red curve is the variety that defines our data.
Linear Compression Auto Encoder
The simplest auto-encoder is a two-layer compressive auto-encoder with linear activation functions (more layers do not make sense with linear activation).
Such an auto-encoder searches for an affine (linear with a shift) subspace in the space of objects that describes the greatest variation in objects, the PCA (principal component method) does the same thing, and both of them find the same subspace
from keras.layers import Input, Dense
from keras.models import Model
from keras.optimizers import Adam
def linear_ae():
input_dots = Input((2,))
code = Dense(1, activation='linear')(input_dots)
out = Dense(2, activation='linear')(code)
ae = Model(input_dots, out)
return ae
ae = linear_ae()
ae.compile(Adam(0.01), 'mse')
ae.fit(dots, dots, epochs=15, batch_size=30, verbose=0)
# Применение линейного автоэнкодера
pdots = ae.predict(dots, batch_size=30)
vpdots = pdots[idxs]
# Применение PCA
from sklearn.decomposition import PCA
pca = PCA(1)
pdots_pca = pca.inverse_transform(pca.fit_transform(dots))
Visualization
# Визуализация
plt.figure(figsize=(12, 10))
plt.xlim([-2.5, 2.5])
plt.scatter(dots[:, 0], dots[:, 1], zorder=1)
plt.plot(x1, fx, color="red", linewidth=4, zorder=10)
plt.plot(pdots[:,0], pdots[:,1], color='white', linewidth=12, zorder=3)
plt.plot(pdots_pca[:,0], pdots_pca[:,1], color='orange', linewidth=4, zorder=4)
plt.scatter(vpdots[:,0], vpdots[:,1], color=colors*5, marker='*', s=150, zorder=5)
plt.scatter(vdots[:,0], vdots[:,1], color=colors*5, s=150, zorder=6)
plt.grid(False)
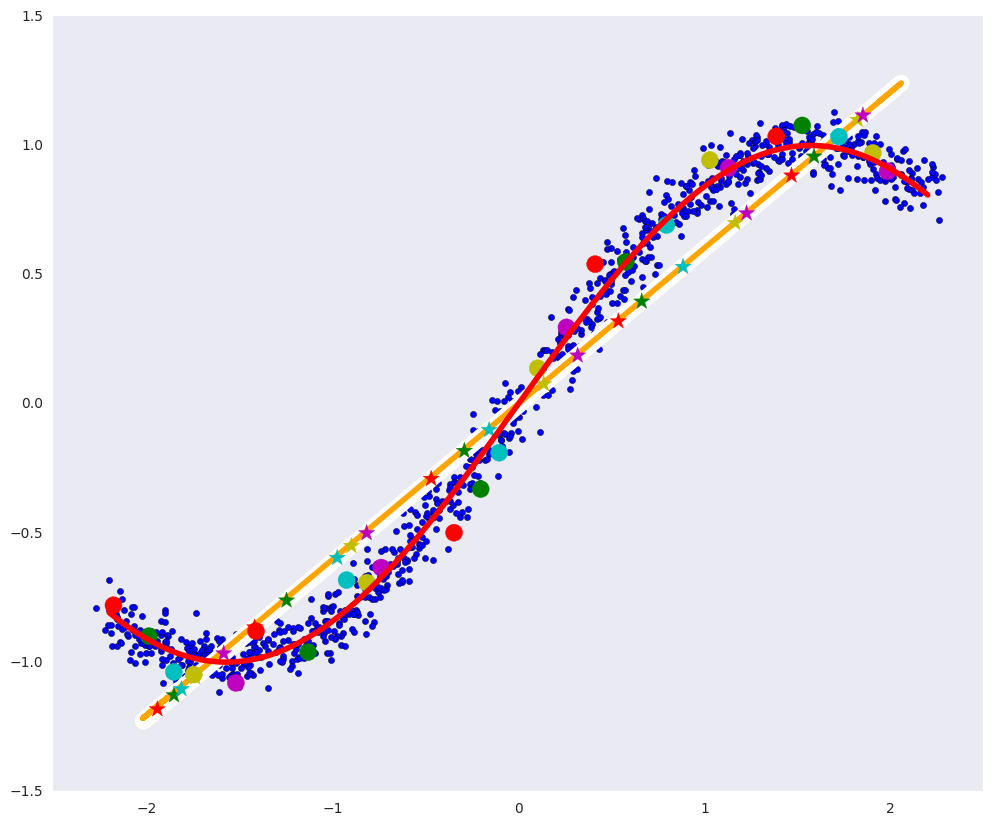
In the picture above:
- the white line is the variety into which the blue data points go after the auto-encoder, that is, an attempt by the auto-encoder to build a manifold that defines the most variations in the data,
- the orange line is the variety into which the blue data points go after the PCA,
- multi-colored circles - dots that turn into stars of the corresponding color after the auto encoder,
- multi-colored stars - respectively, the images of the circles after the auto-encoder.
An auto encoder looking for linear dependencies may not be as useful as an auto encoder that can find arbitrary dependencies in data. It would be useful if both the encoder and the decoder could approximate arbitrary functions. If you add at least one layer of sufficient size and a non-linear activation function between them in the encoder and the decoder, they can find arbitrary dependencies.
Deep Auto Encoder
A deep auto-encoder has more layers and, most importantly, a nonlinear activation function between them (in our case, ELU - Exponential Linear Unit).
def deep_ae():
input_dots = Input((2,))
x = Dense(64, activation='elu')(input_dots)
x = Dense(64, activation='elu')(x)
code = Dense(1, activation='linear')(x)
x = Dense(64, activation='elu')(code)
x = Dense(64, activation='elu')(x)
out = Dense(2, activation='linear')(x)
ae = Model(input_dots, out)
return ae
dae = deep_ae()
dae.compile(Adam(0.003), 'mse')
dae.fit(dots, dots, epochs=200, batch_size=30, verbose=0)
pdots_d = dae.predict(dots, batch_size=30)
vpdots_d = pdots_d[idxs]
Visualization
# Визуализация
plt.figure(figsize=(12, 10))
plt.xlim([-2.5, 2.5])
plt.scatter(dots[:, 0], dots[:, 1], zorder=1)
plt.plot(x1, fx, color="red", linewidth=4, zorder=10)
plt.plot(pdots_d[:,0], pdots_d[:,1], color='white', linewidth=12, zorder=3)
plt.plot(pdots_pca[:,0], pdots_pca[:,1], color='orange', linewidth=4, zorder=4)
plt.scatter(vpdots_d[:,0], vpdots_d[:,1], color=colors*5, marker='*', s=150, zorder=5)
plt.scatter(vdots[:,0], vdots[:,1], color=colors*5, s=150, zorder=6)
plt.grid(False)
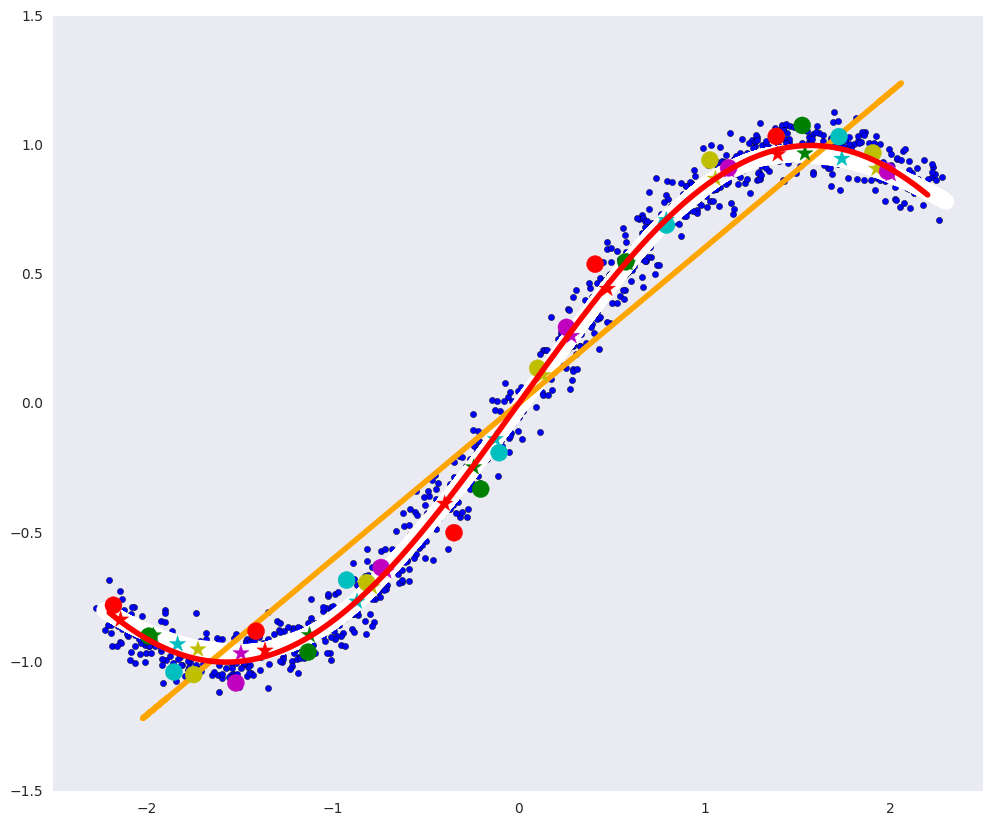
At such an auto encoder, it was almost perfectly possible to build a defining diversity: the white curve almost coincides with the red one.
A deep auto-encoder can theoretically find a manifold of arbitrary complexity, for example, one near which there are numbers in 784-dimensional space.
If we take two objects and look at the objects lying on an arbitrary curve between them, then most likely the intermediate objects will not belong to the general population, since the variety on which the general population lies can be very curved and small.
Let's go back to the dataset of handwritten numbers from the previous part.
First, we move in a straight line in the space of numbers from one 8 to another:
The code
from keras.layers import Conv2D, MaxPooling2D, UpSampling2D
from keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test .astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1))
x_test = np.reshape(x_test, (len(x_test), 28, 28, 1))
# Сверточный автоэнкодер
def create_deep_conv_ae():
input_img = Input(shape=(28, 28, 1))
x = Conv2D(128, (7, 7), activation='relu', padding='same')(input_img)
x = MaxPooling2D((2, 2), padding='same')(x)
x = Conv2D(32, (2, 2), activation='relu', padding='same')(x)
x = MaxPooling2D((2, 2), padding='same')(x)
encoded = Conv2D(1, (7, 7), activation='relu', padding='same')(x)
# На этом моменте представление (7, 7, 1) т.е. 49-размерное
input_encoded = Input(shape=(7, 7, 1))
x = Conv2D(32, (7, 7), activation='relu', padding='same')(input_encoded)
x = UpSampling2D((2, 2))(x)
x = Conv2D(128, (2, 2), activation='relu', padding='same')(x)
x = UpSampling2D((2, 2))(x)
decoded = Conv2D(1, (7, 7), activation='sigmoid', padding='same')(x)
# Модели
encoder = Model(input_img, encoded, name="encoder")
decoder = Model(input_encoded, decoded, name="decoder")
autoencoder = Model(input_img, decoder(encoder(input_img)), name="autoencoder")
return encoder, decoder, autoencoder
c_encoder, c_decoder, c_autoencoder = create_deep_conv_ae()
c_autoencoder.compile(optimizer='adam', loss='binary_crossentropy')
c_autoencoder.fit(x_train, x_train,
epochs=50,
batch_size=256,
shuffle=True,
validation_data=(x_test, x_test))
def plot_digits(*args):
args = [x.squeeze() for x in args]
n = min([x.shape[0] for x in args])
plt.figure(figsize=(2*n, 2*len(args)))
for j in range(n):
for i in range(len(args)):
ax = plt.subplot(len(args), n, i*n + j + 1)
plt.imshow(args[i][j])
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
# Гомотопия по прямой между объектами или между кодами
def plot_homotopy(frm, to, n=10, decoder=None):
z = np.zeros(([n] + list(frm.shape)))
for i, t in enumerate(np.linspace(0., 1., n)):
z[i] = frm * (1-t) + to * t
if decoder:
plot_digits(decoder.predict(z, batch_size=n))
else:
plot_digits(z)
# Гомотопия между первыми двумя восьмерками
frm, to = x_test[y_test == 8][1:3]
plot_homotopy(frm, to)

If we move along the curve between the codes (and if the variety of codes is well parameterized), then the decoder will translate this curve from the code space into a curve that does not leave the defining variety in the space of objects. That is, intermediate objects on the curve will belong to the population.
codes = c_encoder.predict(x_test[y_test == 8][1:3])
plot_homotopy(codes[0], codes[1], n=10, decoder=c_decoder)

Intermediate numbers are quite good eights.
Thus, we can say that the auto-encoder, at least locally, has learned the form of the defining manifold.
Retraining Auto Encoder
In order for the autoencoder to learn how to isolate some complex patterns, the generalizing abilities of the encoder and decoder must be limited, otherwise even an autoencoder with a one-dimensional code can simply draw a one-dimensional curve through each point in the training set, i.e. just remember every object. But this complex variety, which the auto-encoder will build, will not have much in common with the variety determining the general population.
Take the same problem with artificial data, train the same deep auto-encoder on a very small subset of points and look at the resulting manifold:
The code
dae = deep_ae()
dae.compile(Adam(0.0003), 'mse')
x_train_oft = np.vstack([dots[idxs]]*4000)
dae.fit(x_train_oft, x_train_oft, epochs=200, batch_size=15, verbose=1)
pdots_d = dae.predict(dots, batch_size=30)
vpdots_d = pdots_d[idxs]
plt.figure(figsize=(12, 10))
plt.xlim([-2.5, 2.5])
plt.scatter(dots[:, 0], dots[:, 1], zorder=1)
plt.plot(x1, fx, color="red", linewidth=4, zorder=10)
plt.plot(pdots_d[:,0], pdots_d[:,1], color='white', linewidth=6, zorder=3)
plt.plot(pdots_pca[:,0], pdots_pca[:,1], color='orange', linewidth=4, zorder=4)
plt.scatter(vpdots_d[:,0], vpdots_d[:,1], color=colors*5, marker='*', s=150, zorder=5)
plt.scatter(vdots[:,0], vdots[:,1], color=colors*5, s=150, zorder=6)
plt.grid(False)

It can be seen that the white curve passed through each data point and is weakly similar to the red curve defining the data: typical retraining on the face.
Hidden variables
We can consider the general population as some process of data generation
- desired number
- stroke thickness
- tilt numbers
- neatness
- etc.
Each of these factors has its own a priori distribution, for example, the probability that a figure eight will be drawn is the Bernoulli distribution with a probability of 1/10, the stroke thickness also has some distribution of its own and can depend on both accuracy and its hidden variables, such like the thickness of a pen or the temperament of a person (again with its distributions).
In the learning process, the auto-encoder itself must come to hidden factors, for example, such as those listed above, some complex combinations of them, or even completely different ones. However, the joint distribution that he will learn does not have to be simple at all, it may be some kind of complex curve area. (It is possible to pass values to the decoder from outside this area, only the results will no longer be from the defining manifold, but from its random continuous extension).
That is why we cannot simply generate new ones
For definiteness, we introduce some notation using the example of numbers:
- random size of the picture 28x28,
- a random value of the hidden factors that determine the figure in the picture,
- the probabilistic distribution of the images of numbers in the pictures, i.e. the probability of a particular image of a figure, in principle, be drawn (if the picture does not look like a number, then this probability is extremely small),
- the probability distribution of hidden factors, for example, the distribution of the stroke thickness,
- probability distribution of hidden factors for a given picture (a different combination of hidden variables and noise can lead to the same picture),
- the probability distribution of pictures for given hidden factors, the same factors can lead to different pictures (the same person in the same conditions does not draw exactly the same numbers),
- joint distribution
and
, the most complete understanding of the data necessary for the generation of new objects.
Let's see how the hidden variables are distributed in a regular auto-encoder:
The code
from keras.layers import Flatten, Reshape
from keras.regularizers import L1L2
def create_deep_sparse_ae(lambda_l1):
# Размерность кодированного представления
encoding_dim = 16
# Энкодер
input_img = Input(shape=(28, 28, 1))
flat_img = Flatten()(input_img)
x = Dense(encoding_dim*4, activation='relu')(flat_img)
x = Dense(encoding_dim*3, activation='relu')(x)
x = Dense(encoding_dim*2, activation='relu')(x)
encoded = Dense(encoding_dim, activation='linear', activity_regularizer=L1L2(lambda_l1, 0))(x)
# Декодер
input_encoded = Input(shape=(encoding_dim,))
x = Dense(encoding_dim*2, activation='relu')(input_encoded)
x = Dense(encoding_dim*3, activation='relu')(x)
x = Dense(encoding_dim*4, activation='relu')(x)
flat_decoded = Dense(28*28, activation='sigmoid')(x)
decoded = Reshape((28, 28, 1))(flat_decoded)
# Модели
encoder = Model(input_img, encoded, name="encoder")
decoder = Model(input_encoded, decoded, name="decoder")
autoencoder = Model(input_img, decoder(encoder(input_img)), name="autoencoder")
return encoder, decoder, autoencoder
encoder, decoder, autoencoder = create_deep_sparse_ae(0.)
autoencoder.compile(optimizer=Adam(0.0003), loss='binary_crossentropy')
autoencoder.fit(x_train, x_train,
epochs=100,
batch_size=64,
shuffle=True,
validation_data=(x_test, x_test))
n = 10
imgs = x_test[:n]
decoded_imgs = autoencoder.predict(imgs, batch_size=n)
plot_digits(imgs, decoded_imgs)
This is how the images restored by this encoder look like:
Images

Joint distribution of hidden variables
codes = encoder.predict(x_test)
sns.jointplot(codes[:,1], codes[:,3])

It can be seen that the joint distribution
Is there any way to control the distribution of hidden variables
The easiest way is to add a regularizer
The regularizer forces the auto-encoder to look for hidden variables that are distributed according to the necessary laws, whether he succeeds is another question. However, this does not force them to be independent, i.e.
Let's look at the joint distribution of hidden parameters in a sparse auto-encoder.
Code and visualization
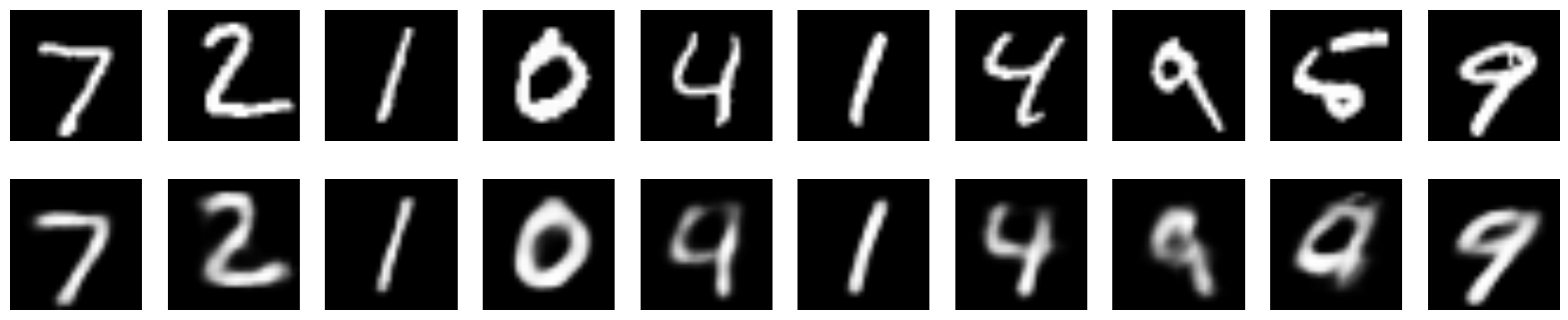
s_encoder, s_decoder, s_autoencoder = create_deep_sparse_ae(0.00001)
s_autoencoder.compile(optimizer=Adam(0.0003), loss='binary_crossentropy')
s_autoencoder.fit(x_train, x_train, epochs=200, batch_size=256, shuffle=True,
validation_data=(x_test, x_test))
imgs = x_test[:n]
decoded_imgs = s_autoencoder.predict(imgs, batch_size=n)
plot_digits(imgs, decoded_imgs)
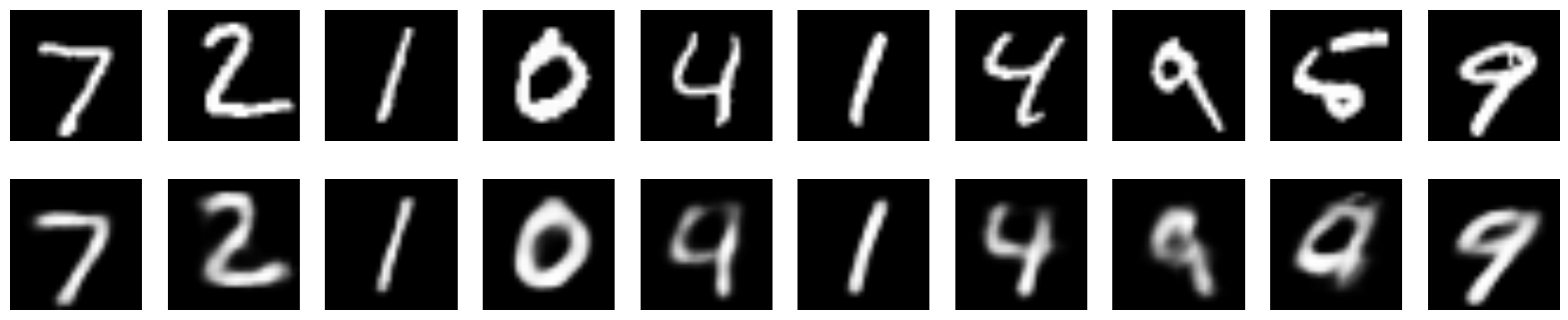
codes = s_encoder.predict(x_test)
snt.jointplot(codes[:,1], codes[:,3])

About how to control the hidden space so that it is already possible to intelligently generate images from it - in the next part about variational autoencoders (VAE).
Useful links and literature
This post is based on the chapter on Auto Encoders (specifically the Learning maifolds with autoencoders subheading ) in the Deep Learning Book .
