The math in Gamedev is simple. Matrices and Affine Transformations
Hello! My name is Grisha, and I am the founder of CGDevs. Today I want to continue the topic of mathematics in game dev. The previous article showed basic examples of the use of vectors and integrals in Unity projects, and now let's talk about matrices and affine transformations. If you are well versed in matrix arithmetic; you know what TRS is and how to work with it; What is a Householder Transformation - you may not find anything new for yourself. We will speak in the context of 3D graphics. If you are interested in this topic - welcome under cat.

Let's start with one of the most important concepts in the context of the article - affine transformations . Affine transformations are, in fact, a transformation of a coordinate system (or space) by multiplying a vector by a special matrix. For example, such transformations as displacement, rotation, scaling, reflection, etc. The main properties of affine transformations are that you remain in the same space (it is impossible to make a two-dimensional vector two-dimensional) and that if the lines intersect / were parallel / were crossed before the transformation, then this property after the transformation is preserved. In addition, they have a lot of mathematical properties that require knowledge of the theory of groups, sets and linear algebra, which makes it easier to work with them.
The second important concept in computer graphics is the TRS matrix . With it you can describe the most frequent operations used when working with computer graphics. The TRS matrix is a composition of three transformation matrices. Matrix of translation (Translation), rotation on each axis (Rotation) and scaling (Scale).
It looks like this.
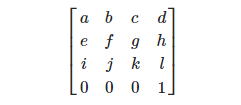
Where:
Move is t = new Vector3 (d, h, l).
Scaling - s = new Vector3 (new Vector3 (a, e, i) .magnitude, new Vector3 (b, f, j) .magnitude, new Vector3 (c, g, k) .magnitude);
Rotation is a matrix of the form:
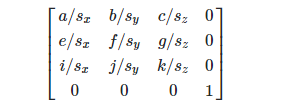
Now let's move a little deeper into the Unity context. Let's start with the fact that the TRS matrix is a very convenient thing, but it should not be used everywhere. Since a simple indication of the position or the addition of vectors in a unit will work faster, but in many mathematical algorithms the matrix is many times more convenient than vectors. The functionality of TRS in Unity is largely implemented in the class Matrix4x4 , but it is not convenient from the point of view of application. Since in addition to applying a matrix through multiplication, it can generally store information about the orientation of an object, as well as for some transformations you want to be able to calculate not only the position, but also change the orientation of the object as a whole (for example, a reflection that is not implemented in Unity)
All the examples below are for the local coordinate system (the origin of the GameObject is the origin of the object. If the object is the root of the hierarchy in the unit, then the origin is the world (0,0,0)).
Since using the TRS matrix it is possible in principle to describe the position of an object in space, we need decomposition from the TRS into specific values of position, rotation and scale for Unity. To do this, you can write extension methods for the Matrix4x4 class.
In addition, for convenient operation, you can implement a couple of extensions of the Transform class in order to work in it with TRS.
The advantages of the unit end here, since the matrices in Unity are very poor in operation. For many algorithms, matrix arithmetic is needed, which in a unit is not implemented even in completely basic operations, such as matrix addition and matrix multiplication by a scalar. In addition, due to the feature of implementing vectors in Unity3d, there is also a number of inconveniences due to the fact that you can make a 4x1 vector, but you cannot make 1x4 out of the box. Since we’ll talk about Householder transformation for reflections, we first implement the necessary operations for this.
On addition / subtraction and multiplication by a scalar - everything is simple. It looks quite cumbersome, but there is nothing difficult here, since arithmetic is simple.
But to reflect, we need the operation of multiplying matrices in a particular case. Multiplying a vector of dimension 4x1 by 1x4 (transposed) If you are familiar with matrix mathematics, then you know that with this multiplication, you need to look at the extreme figures of the dimension, and you get the dimension of the matrix at the output, that is, in this case 4x4. Information on how matrices are multiplied is sufficient, so we will not paint it. For example, here is a specific case implemented, which will be useful to us in the future.
In search of how to reflect an object with respect to any axis, I often meet the advice to put a negative scale in the necessary direction. This is very bad advice in the context of Unity, since it breaks down a lot of systems in the engine (batching, collisions, etc.) In some algorithms, this turns into quite nontrivial calculations, if you need to reflect in a trite way about Vector3.up or Vector3.forward, but in any direction. The method of reflection in a unit out of the box is not implemented, so I implemented the Householder method .
Household Transformation, is used not only in computer graphics, but in this context it is a linear transformation that reflects an object relative to a plane that passes through the "origin" and is determined by the normal to the plane. In many sources, it is described quite difficult, and incomprehensible, although its formula is elementary.
H = I-2 * n * (n ^ T)
Where H is the transformation matrix, I in this case is Matrix4x4.identity, and n = new Vector4 (planeNormal.x, planeNormal.y, planeNormal.z, 0). The symbol T means transposition, that is, after multiplying n * (n ^ T), we get a 4x4 matrix.
Here the implemented methods come in handy and the recording will turn out to be very compact.
Important: planeNormal should be normalized (which is logical), and the last coordinate n is 0, so that there is no effect of stretching in the direction, since it depends on the length of the vector n.
Now for the convenience of working in Unity, we implement the extension method for the
That's all for today, if this cycle of articles continues to be interesting further, I will reveal other applications of mathematics in game development. This time the project will not be, as all the code is placed in the article, but the project with a specific application will be in the next article. From the picture you can guess what the next article will be.

Thanks for attention!

Let's start with one of the most important concepts in the context of the article - affine transformations . Affine transformations are, in fact, a transformation of a coordinate system (or space) by multiplying a vector by a special matrix. For example, such transformations as displacement, rotation, scaling, reflection, etc. The main properties of affine transformations are that you remain in the same space (it is impossible to make a two-dimensional vector two-dimensional) and that if the lines intersect / were parallel / were crossed before the transformation, then this property after the transformation is preserved. In addition, they have a lot of mathematical properties that require knowledge of the theory of groups, sets and linear algebra, which makes it easier to work with them.
TRS matrix
The second important concept in computer graphics is the TRS matrix . With it you can describe the most frequent operations used when working with computer graphics. The TRS matrix is a composition of three transformation matrices. Matrix of translation (Translation), rotation on each axis (Rotation) and scaling (Scale).
It looks like this.
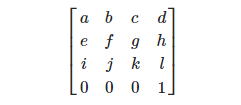
Where:
Move is t = new Vector3 (d, h, l).
Scaling - s = new Vector3 (new Vector3 (a, e, i) .magnitude, new Vector3 (b, f, j) .magnitude, new Vector3 (c, g, k) .magnitude);
Rotation is a matrix of the form:
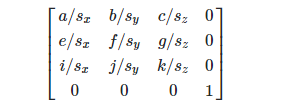
Now let's move a little deeper into the Unity context. Let's start with the fact that the TRS matrix is a very convenient thing, but it should not be used everywhere. Since a simple indication of the position or the addition of vectors in a unit will work faster, but in many mathematical algorithms the matrix is many times more convenient than vectors. The functionality of TRS in Unity is largely implemented in the class Matrix4x4 , but it is not convenient from the point of view of application. Since in addition to applying a matrix through multiplication, it can generally store information about the orientation of an object, as well as for some transformations you want to be able to calculate not only the position, but also change the orientation of the object as a whole (for example, a reflection that is not implemented in Unity)
All the examples below are for the local coordinate system (the origin of the GameObject is the origin of the object. If the object is the root of the hierarchy in the unit, then the origin is the world (0,0,0)).
Since using the TRS matrix it is possible in principle to describe the position of an object in space, we need decomposition from the TRS into specific values of position, rotation and scale for Unity. To do this, you can write extension methods for the Matrix4x4 class.
Getting the position, turn and scale
publicstatic Vector3 ExtractPosition(this Matrix4x4 matrix)
{
Vector3 position;
position.x = matrix.m03;
position.y = matrix.m13;
position.z = matrix.m23;
return position;
}
publicstatic Quaternion ExtractRotation(this Matrix4x4 matrix)
{
Vector3 forward;
forward.x = matrix.m02;
forward.y = matrix.m12;
forward.z = matrix.m22;
Vector3 upwards;
upwards.x = matrix.m01;
upwards.y = matrix.m11;
upwards.z = matrix.m21;
return Quaternion.LookRotation(forward, upwards);
}
publicstatic Vector3 ExtractScale(this Matrix4x4 matrix)
{
Vector3 scale;
scale.x = new Vector4(matrix.m00, matrix.m10, matrix.m20, matrix.m30).magnitude;
scale.y = new Vector4(matrix.m01, matrix.m11, matrix.m21, matrix.m31).magnitude;
scale.z = new Vector4(matrix.m02, matrix.m12, matrix.m22, matrix.m32).magnitude;
return scale;
}In addition, for convenient operation, you can implement a couple of extensions of the Transform class in order to work in it with TRS.
Extension transform
publicstaticvoidApplyLocalTRS(this Transform tr, Matrix4x4 trs)
{
tr.localPosition = trs.ExtractPosition();
tr.localRotation = trs.ExtractRotation();
tr.localScale = trs.ExtractScale();
}
publicstatic Matrix4x4 ExtractLocalTRS(this Transform tr)
{
return Matrix4x4.TRS(tr.localPosition, tr.localRotation, tr.localScale);
}The advantages of the unit end here, since the matrices in Unity are very poor in operation. For many algorithms, matrix arithmetic is needed, which in a unit is not implemented even in completely basic operations, such as matrix addition and matrix multiplication by a scalar. In addition, due to the feature of implementing vectors in Unity3d, there is also a number of inconveniences due to the fact that you can make a 4x1 vector, but you cannot make 1x4 out of the box. Since we’ll talk about Householder transformation for reflections, we first implement the necessary operations for this.
On addition / subtraction and multiplication by a scalar - everything is simple. It looks quite cumbersome, but there is nothing difficult here, since arithmetic is simple.
Basic Matrix Operations
publicstatic Matrix4x4 MutiplyByNumber(this Matrix4x4 matrix, float number)
{
returnnew Matrix4x4(
new Vector4(matrix.m00 * number, matrix.m10 * number, matrix.m20 * number, matrix.m30 * number),
new Vector4(matrix.m01 * number, matrix.m11 * number, matrix.m21 * number, matrix.m31 * number),
new Vector4(matrix.m02 * number, matrix.m12 * number, matrix.m22 * number, matrix.m32 * number),
new Vector4(matrix.m03 * number, matrix.m13 * number, matrix.m23 * number, matrix.m33 * number)
);
}
publicstatic Matrix4x4 DivideByNumber(this Matrix4x4 matrix, float number)
{
returnnew Matrix4x4(
new Vector4(matrix.m00 / number, matrix.m10 / number, matrix.m20 / number, matrix.m30 / number),
new Vector4(matrix.m01 / number, matrix.m11 / number, matrix.m21 / number, matrix.m31 / number),
new Vector4(matrix.m02 / number, matrix.m12 / number, matrix.m22 / number, matrix.m32 / number),
new Vector4(matrix.m03 / number, matrix.m13 / number, matrix.m23 / number, matrix.m33 / number)
);
}
publicstatic Matrix4x4 Plus(this Matrix4x4 matrix, Matrix4x4 matrixToAdding)
{
returnnew Matrix4x4(
new Vector4(matrix.m00 + matrixToAdding.m00, matrix.m10 + matrixToAdding.m10,
matrix.m20 + matrixToAdding.m20, matrix.m30 + matrixToAdding.m30),
new Vector4(matrix.m01 + matrixToAdding.m01, matrix.m11 + matrixToAdding.m11,
matrix.m21 + matrixToAdding.m21, matrix.m31 + matrixToAdding.m31),
new Vector4(matrix.m02 + matrixToAdding.m02, matrix.m12 + matrixToAdding.m12,
matrix.m22 + matrixToAdding.m22, matrix.m32 + matrixToAdding.m32),
new Vector4(matrix.m03 + matrixToAdding.m03, matrix.m13 + matrixToAdding.m13,
matrix.m23 + matrixToAdding.m23, matrix.m33 + matrixToAdding.m33)
);
}
publicstatic Matrix4x4 Minus(this Matrix4x4 matrix, Matrix4x4 matrixToMinus)
{
returnnew Matrix4x4(
new Vector4(matrix.m00 - matrixToMinus.m00, matrix.m10 - matrixToMinus.m10,
matrix.m20 - matrixToMinus.m20, matrix.m30 - matrixToMinus.m30),
new Vector4(matrix.m01 - matrixToMinus.m01, matrix.m11 - matrixToMinus.m11,
matrix.m21 - matrixToMinus.m21, matrix.m31 - matrixToMinus.m31),
new Vector4(matrix.m02 - matrixToMinus.m02, matrix.m12 - matrixToMinus.m12,
matrix.m22 - matrixToMinus.m22, matrix.m32 - matrixToMinus.m32),
new Vector4(matrix.m03 - matrixToMinus.m03, matrix.m13 - matrixToMinus.m13,
matrix.m23 - matrixToMinus.m23, matrix.m33 - matrixToMinus.m33)
);
}But to reflect, we need the operation of multiplying matrices in a particular case. Multiplying a vector of dimension 4x1 by 1x4 (transposed) If you are familiar with matrix mathematics, then you know that with this multiplication, you need to look at the extreme figures of the dimension, and you get the dimension of the matrix at the output, that is, in this case 4x4. Information on how matrices are multiplied is sufficient, so we will not paint it. For example, here is a specific case implemented, which will be useful to us in the future.
Multiplication of vector by transposed
publicstatic Matrix4x4 MultiplyVectorsTransposed(Vector4 vector, Vector4 transposeVector)
{
float[] vectorPoints = new[] {vector.x, vector.y, vector.z, vector.w},
transposedVectorPoints = new[]
{transposeVector.x, transposeVector.y, transposeVector.z, transposeVector.w};
int matrixDimension = vectorPoints.Length;
float[] values = newfloat[matrixDimension * matrixDimension];
for (int i = 0; i < matrixDimension; i++)
{
for (int j = 0; j < matrixDimension; j++)
{
values[i + j * matrixDimension] = vectorPoints[i] * transposedVectorPoints[j];
}
}
returnnew Matrix4x4(
new Vector4(values[0], values[1], values[2], values[3]),
new Vector4(values[4], values[5], values[6], values[7]),
new Vector4(values[8], values[9], values[10], values[11]),
new Vector4(values[12], values[13], values[14], values[15])
);
}Household Transformation
In search of how to reflect an object with respect to any axis, I often meet the advice to put a negative scale in the necessary direction. This is very bad advice in the context of Unity, since it breaks down a lot of systems in the engine (batching, collisions, etc.) In some algorithms, this turns into quite nontrivial calculations, if you need to reflect in a trite way about Vector3.up or Vector3.forward, but in any direction. The method of reflection in a unit out of the box is not implemented, so I implemented the Householder method .
Household Transformation, is used not only in computer graphics, but in this context it is a linear transformation that reflects an object relative to a plane that passes through the "origin" and is determined by the normal to the plane. In many sources, it is described quite difficult, and incomprehensible, although its formula is elementary.
H = I-2 * n * (n ^ T)
Where H is the transformation matrix, I in this case is Matrix4x4.identity, and n = new Vector4 (planeNormal.x, planeNormal.y, planeNormal.z, 0). The symbol T means transposition, that is, after multiplying n * (n ^ T), we get a 4x4 matrix.
Here the implemented methods come in handy and the recording will turn out to be very compact.
Household Transformation
publicstatic Matrix4x4 HouseholderReflection(this Matrix4x4 matrix4X4, Vector3 planeNormal)
{
planeNormal.Normalize();
Vector4 planeNormal4 = new Vector4(planeNormal.x, planeNormal.y, planeNormal.z, 0);
Matrix4x4 householderMatrix = Matrix4x4.identity.Minus(
MultiplyVectorsTransposed(planeNormal4, planeNormal4).MutiplyByNumber(2));
return householderMatrix * matrix4X4;
}Important: planeNormal should be normalized (which is logical), and the last coordinate n is 0, so that there is no effect of stretching in the direction, since it depends on the length of the vector n.
Now for the convenience of working in Unity, we implement the extension method for the
The reflection of the transformation in the local coordinate system
publicstaticvoidLocalReflect(this Transform tr, Vector3 planeNormal)
{
var trs = tr.ExtractLocalTRS();
var reflected = trs.HouseholderReflection(planeNormal);
tr.ApplyLocalTRS(reflected);
}That's all for today, if this cycle of articles continues to be interesting further, I will reveal other applications of mathematics in game development. This time the project will not be, as all the code is placed in the article, but the project with a specific application will be in the next article. From the picture you can guess what the next article will be.

Thanks for attention!
