Analysis of the report of Andrey Akinshin about arithmetic
Hello everyone, one more analysis is ready. Today we will not watch the report with JPoint, but with DotNext! The author of the report is Andrey DreamWalker Akinshin, and his presentation is devoted to the details of the implementation of floating-point arithmetic in .NET:
Slides can be found here .
Disclaimer: about the implementation of arithmetic, only the parsed report itself, and not the actual article.
At this point, I must say that I do not really like puzzle pieces. They require knowledge of the gloomy corners of the specification, which in real life is usually useless. Just imagine that you accompany the code written by a lover of riddles.
Note that getting a person to think about something important before telling him “how to” is generally good, he will remember the result much better. But to begin with the essence, that is, to choose the knowledge that needs to be transmitted to people, and to illustrate it with a paradoxical task with simple conditions, is difficult. It is often easier for puzzlers to take those things that are not very critical to remember, but no one knows them, and make them pure entertainment.
In general, an attentive reader can easily trace my dislike of the genre in this article.
Is there any contradiction here: assistants come to the scene to create the illusion of competition, but it is clear that the answers and transitional remarks between tasks are known in advance. For example, at 12: 00-12: 20 Julia argues that casting to the whole is not the right operation, and you need to use rounding, and then the next task appears, just for rounding. In such situations, I would change the order of tasks so that the topic that supposedly “came to the head” of the assistant would not arise immediately, but a little later. For greater credibility, assistants might sometimes agree with each other.
Also it seems to me an unfortunate cameo of Andrei Dmitriev (39:00). It is clear why this sketch is needed: to advertise the next DotNext and the next report. But since we are saying that time has run out, although there are still problems, then let everything look as if it is true. Firstly, to speak “barely” and not say that we have a few more minutes to answer questions. Secondly, to highlight two or three additional tasks with answers and scroll through slides with them at the time of interruption. Then the people, you see, will be interested, suddenly the Zeigarnik effect will work, the presentation will be downloaded, everyone is fine.
And so I remained perplexed: what was it all about? Integral more ...
In some places, I didn’t have an understanding of what exactly the specification developers smoked. Why did they do just that? This would help not only to remember better, but also to separate important tasks from random nonsense. Let's look, for example, at the previously mentioned rounding (starts at 12:20):

Where did rounding to the nearest even come from? Why is it turned on by default? When is the “away from zero” mode needed? Perhaps I just missed everything, and normal people have known for a long time, but for the first time in my life I understood this question in the preparation of this analysis. It turns out that the regime is called "banking rounding" and was invented mainly for cases when you need to add money with cents / kopecks in a fractional part. Since there are only 100 different cents, a tail of exactly 50 cents will occur quite often in a random set of monetary amounts. If all of them are rounded off from zero, we will accumulate a systematic error, and if to the nearest even, then the rounding errors will average about zero. Moreover, each specific number is rounded deterministically, and not in a random direction (and that is, such an approach).
Since it is not necessary to count money using float and double for many reasons, the default settings look illogical. But at least it’s clear what is behind them. And if someone knows another realistic scenario for using bank rounding, please share.
It seems to me that raising the logic behind the specification and telling it to the audience is good and good. Remembering not only the facts, but also their causes is much more convenient.
So who will now remember the truth table for the operations from exercise 8 (beginning 17:23), although it was in the presentation?
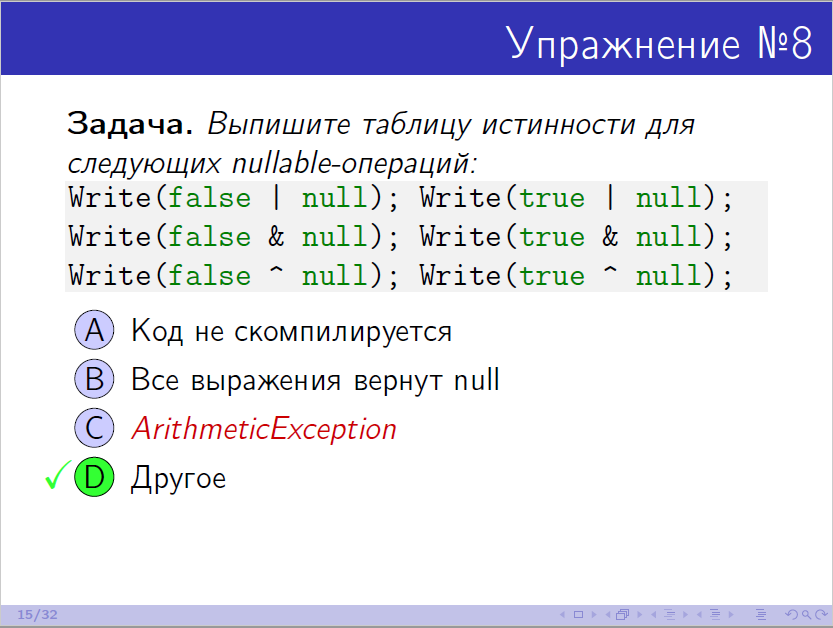
Is it generally important to know? If we understood the usage scenarios that the developers had in mind, it would be easier to restore it.
On the contrary, the relevance of exercise 10 cannot be called into question (beginning at 21:18):
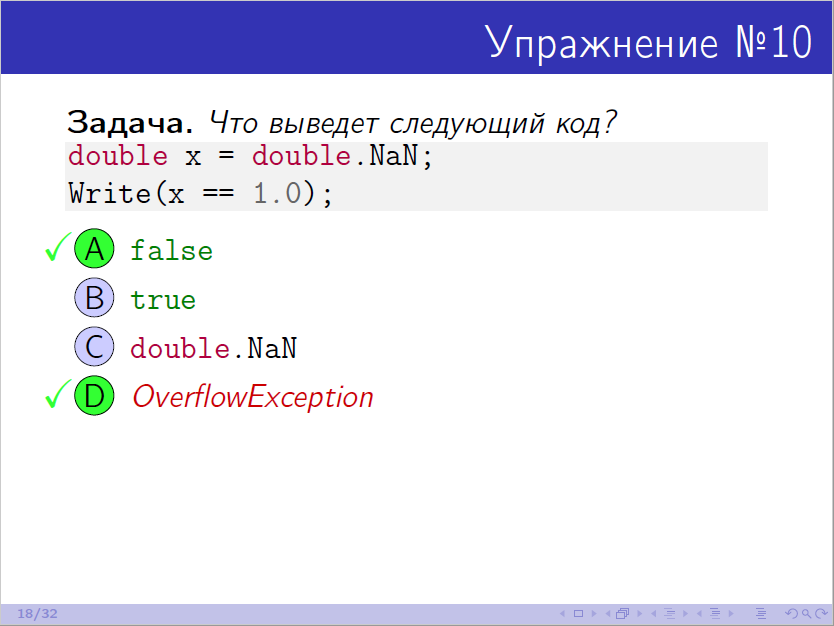
Andrey talks about the situations in which you can step on a problem with OverflowException and ends the story with an optimistic desire to be more careful. Did everyone understand right away how to be more careful? Details would not be in the way.
Of course, in the university we had fragments of courses, and even entire courses on data presentation. And of course, we were told about floating point numbers there, but without practice a lot is forgotten. In some tasks, Andrei touches on fundamental properties such as float and double and the problems arising from them, but does not quite focus the attention of the audience on this. The most striking example is the problem of associativity (exercise 14, beginning at 31:30):

Given that not everyone in the room answered correctly, the material of the first or second course should be refreshed. In this case, it is important that the numbers are distributed unevenly: the farther from zero, the greater the intervals between them. Let's look at two neighboring floats of maximum order (doubles are the same in meaning, just draw more):


From the point of view of the format in question, there is nothing between them. Moreover, in the real world, the first number is 1.7014122 * 10 38 , the second is 1.701412 * 10 38 , and the difference between them is 0.0000002 * 10 38 . This, let's say carefully, is drop dead. It is impossible to add one, a thousand or even a billion to the number of maximum order.
Knowing this mechanics, it is easy to understand how the rule of associativity is still violated: the sum of several small numbers may turn out to be greater than the distance between two adjacent large numbers, while each small number individually will simply be destroyed if you start addition with a large number.
In general, each puzzler is a fascinating story that gives the speaker credit for the attention of the audience, and you can use this credit to get some morality out of at least some of the riddles (it really is there!). I am sure that the report would benefit from this.
The slides are well done, so I won’t begin to find fault with the little things, but I’ll note decisions worthy of imitation.
The report has a lot of slides with lots of information. It’s hard to make out and understand everything on the screen right away, but Andrei’s elements appear in turn. Thus, the viewer at any moment does not lose the place that you need to look at and about which the speaker speaks. This greatly facilitates the perception of large schemes, pieces of code, lists. Do as Andrew.
Let the presentation have almost no funny pictures, except for Homer Simpson (which, in principle, could be looked for in a better resolution) and the integral, it does not become less fun from this. Math in itself is fun.
At the same time, each exercise is designed in the same way, the solution is highlighted the same, the explanation is marked in the title of the slide - the viewer quickly gets used to it and nothing distracts him from solving the puzzles. If you have a lot of small presentations, it makes sense to stick to a similar design, as in this case.
If you want to receive feedback on your presentation, then I will gladly provide it to you.
Slides can be found here .
Disclaimer: about the implementation of arithmetic, only the parsed report itself, and not the actual article.
Plot
At this point, I must say that I do not really like puzzle pieces. They require knowledge of the gloomy corners of the specification, which in real life is usually useless. Just imagine that you accompany the code written by a lover of riddles.
Note that getting a person to think about something important before telling him “how to” is generally good, he will remember the result much better. But to begin with the essence, that is, to choose the knowledge that needs to be transmitted to people, and to illustrate it with a paradoxical task with simple conditions, is difficult. It is often easier for puzzlers to take those things that are not very critical to remember, but no one knows them, and make them pure entertainment.
In general, an attentive reader can easily trace my dislike of the genre in this article.
Story moves and acting
Is there any contradiction here: assistants come to the scene to create the illusion of competition, but it is clear that the answers and transitional remarks between tasks are known in advance. For example, at 12: 00-12: 20 Julia argues that casting to the whole is not the right operation, and you need to use rounding, and then the next task appears, just for rounding. In such situations, I would change the order of tasks so that the topic that supposedly “came to the head” of the assistant would not arise immediately, but a little later. For greater credibility, assistants might sometimes agree with each other.
Also it seems to me an unfortunate cameo of Andrei Dmitriev (39:00). It is clear why this sketch is needed: to advertise the next DotNext and the next report. But since we are saying that time has run out, although there are still problems, then let everything look as if it is true. Firstly, to speak “barely” and not say that we have a few more minutes to answer questions. Secondly, to highlight two or three additional tasks with answers and scroll through slides with them at the time of interruption. Then the people, you see, will be interested, suddenly the Zeigarnik effect will work, the presentation will be downloaded, everyone is fine.
And so I remained perplexed: what was it all about? Integral more ...
Not only how, but why
In some places, I didn’t have an understanding of what exactly the specification developers smoked. Why did they do just that? This would help not only to remember better, but also to separate important tasks from random nonsense. Let's look, for example, at the previously mentioned rounding (starts at 12:20):

Where did rounding to the nearest even come from? Why is it turned on by default? When is the “away from zero” mode needed? Perhaps I just missed everything, and normal people have known for a long time, but for the first time in my life I understood this question in the preparation of this analysis. It turns out that the regime is called "banking rounding" and was invented mainly for cases when you need to add money with cents / kopecks in a fractional part. Since there are only 100 different cents, a tail of exactly 50 cents will occur quite often in a random set of monetary amounts. If all of them are rounded off from zero, we will accumulate a systematic error, and if to the nearest even, then the rounding errors will average about zero. Moreover, each specific number is rounded deterministically, and not in a random direction (and that is, such an approach).
Since it is not necessary to count money using float and double for many reasons, the default settings look illogical. But at least it’s clear what is behind them. And if someone knows another realistic scenario for using bank rounding, please share.
It seems to me that raising the logic behind the specification and telling it to the audience is good and good. Remembering not only the facts, but also their causes is much more convenient.
So who will now remember the truth table for the operations from exercise 8 (beginning 17:23), although it was in the presentation?

Is it generally important to know? If we understood the usage scenarios that the developers had in mind, it would be easier to restore it.
On the contrary, the relevance of exercise 10 cannot be called into question (beginning at 21:18):

Andrey talks about the situations in which you can step on a problem with OverflowException and ends the story with an optimistic desire to be more careful. Did everyone understand right away how to be more careful? Details would not be in the way.
How float works
Of course, in the university we had fragments of courses, and even entire courses on data presentation. And of course, we were told about floating point numbers there, but without practice a lot is forgotten. In some tasks, Andrei touches on fundamental properties such as float and double and the problems arising from them, but does not quite focus the attention of the audience on this. The most striking example is the problem of associativity (exercise 14, beginning at 31:30):

Given that not everyone in the room answered correctly, the material of the first or second course should be refreshed. In this case, it is important that the numbers are distributed unevenly: the farther from zero, the greater the intervals between them. Let's look at two neighboring floats of maximum order (doubles are the same in meaning, just draw more):


From the point of view of the format in question, there is nothing between them. Moreover, in the real world, the first number is 1.7014122 * 10 38 , the second is 1.701412 * 10 38 , and the difference between them is 0.0000002 * 10 38 . This, let's say carefully, is drop dead. It is impossible to add one, a thousand or even a billion to the number of maximum order.
Knowing this mechanics, it is easy to understand how the rule of associativity is still violated: the sum of several small numbers may turn out to be greater than the distance between two adjacent large numbers, while each small number individually will simply be destroyed if you start addition with a large number.
conclusions
In general, each puzzler is a fascinating story that gives the speaker credit for the attention of the audience, and you can use this credit to get some morality out of at least some of the riddles (it really is there!). I am sure that the report would benefit from this.
Slides
The slides are well done, so I won’t begin to find fault with the little things, but I’ll note decisions worthy of imitation.
Sequential appearance of slide elements
The report has a lot of slides with lots of information. It’s hard to make out and understand everything on the screen right away, but Andrei’s elements appear in turn. Thus, the viewer at any moment does not lose the place that you need to look at and about which the speaker speaks. This greatly facilitates the perception of large schemes, pieces of code, lists. Do as Andrew.
Uniformity
Let the presentation have almost no funny pictures, except for Homer Simpson (which, in principle, could be looked for in a better resolution) and the integral, it does not become less fun from this. Math in itself is fun.
At the same time, each exercise is designed in the same way, the solution is highlighted the same, the explanation is marked in the title of the slide - the viewer quickly gets used to it and nothing distracts him from solving the puzzles. If you have a lot of small presentations, it makes sense to stick to a similar design, as in this case.
Regular reviews
If you want to receive feedback on your presentation, then I will gladly provide it to you.
What is needed for this?
All this needs to be sent to the p0b0rchy habrayuzer , that is, to me. I promise that the review will be constructive and polite, and will also highlight positive aspects, and not just what needs to be improved.
- Link to the video of the speech.
- Link to slides.
- Application from the author. Without the consent of the speaker himself, we will not analyze anything.
All this needs to be sent to the p0b0rchy habrayuzer , that is, to me. I promise that the review will be constructive and polite, and will also highlight positive aspects, and not just what needs to be improved.
