Divide & Conquer over the Strassen algorithm

Hello friends! As students of one notorious educational project, bo_0m and I , after an introductory lecture on the course Advanced Java Programming , got our first homework. It was necessary to implement a program that would multiply matrices. And it would have been all right, but it so coincided that the Joker conference was to be held next week, and our teacher decided to cancel the lesson on this occasion, giving us a few hours of free Friday evening. Do not waste time in vain! Since no one is in a hurry, you can get creative.

Welcome, under the hood ↓

First thing that comes to mind

Probably every student at a technical university had to multiply matrices. The algorithm was always one, namely, a simple cubic method of multiplication. And no matter how it sounds, but this method is not so bad (for matrix dimensions less than 100).

We all started from this:

for (int i = 0; i < A.rows(); i++) {
    for (int j = 0; j < B.columns(); j++) {
	for (int k = 0; k < A.columns(); k++) {
	    C[i][j] += A[i][k] * B[k][j];
	}
    }
}

Looking ahead, I’ll say that we will use a modified version using transposition. This modification is well written here , and not only about it.

Ok, let's go further!

Strassen Algorithm

Perhaps not everyone knows, but the author of the algorithm, Volker Strassen, is not only alive, but also actively teaches, being also an honorary professor at the Department of Mathematics and Statistics of the University of Constance. Be sure to read about this person at least on a wiki .
A bit of theory from Wikipedia:

Let A and B be two (n * n) -matrices, and n be the power of 2. Then we can divide each matrix A and B into four ((n / 2) * (n / 2)) -matrices and express through them product of matrices A and B:

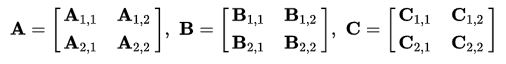
Define new elements:

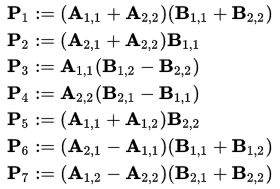
Thus, we need only 7 multiplications at each stage of the recursion. Elements of the matrix C are expressed from Pk by the formulas:

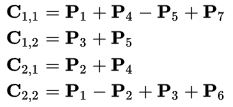
The recursive process continues n times, until the size of the matrices Ci, j becomes small enough, then the usual method of matrix multiplication is used. This is due to the fact that the Strassen algorithm loses efficiency compared to the usual one on small matrices due to a larger number of additions.

let's go to practice!

To implement the Strassen algorithm, we need additional functions. As mentioned above, the algorithm works only with square matrices whose dimension is equal to degree 2; therefore, we bring the original matrices to this form.

For this, a function was implemented that defines a new dimension:

private static int log2(int x) {
    int result = 1;
    while ((x >>= 1) != 0) result++;
    return result;
}
//******************************************************************************************
private static int getNewDimension(int[][] a, int[][] b) {
    return 1 << log2(Collections.max(Arrays.asList(a.length, a[0].length, b[0].length)));
    // Л - Лаконично
}

And a function that expands the matrix to the desired size:

private static int[][] addition2SquareMatrix(int[][] a, int n) {
    int[][] result = new int[n][n];
    for (int i = 0; i < a.length; i++) {
        for (int j = 0; j < a[i].length; j++) {
            result[i][j] = a[i][j];
        }
    }
    return result;
}

Now the source matrices satisfy the requirements for implementing the Strassen algorithm. We also need a function that allows us to split the matrix of size n * n into four matrices (n / 2) * (n / 2) and the inverse to restore the matrix:

private static void splitMatrix(int[][] a, int[][] a11, int[][] a12, int[][] a21, int[][] a22) {
    int n = a.length >> 1;
    for (int i = 0; i < n; i++) {
        System.arraycopy(a[i], 0, a11[i], 0, n);
        System.arraycopy(a[i], n, a12[i], 0, n);
        System.arraycopy(a[i + n], 0, a21[i], 0, n);
        System.arraycopy(a[i + n], n, a22[i], 0, n);
    }
}
 //******************************************************************************************
private static int[][] collectMatrix(int[][] a11, int[][] a12, int[][] a21, int[][] a22) {
    int n = a11.length;
    int[][] a = new int[n << 1][n << 1];
    for (int i = 0; i < n; i++) {
        System.arraycopy(a11[i], 0, a[i], 0, n);
        System.arraycopy(a12[i], 0, a[i], n, n);
        System.arraycopy(a22[i], 0, a[i + n], n, n);
    }
    return a;
}

So we got to the most interesting, the main function of matrix multiplication by the Strassen algorithm is as follows:


This could be the end. The implemented algorithm works as homework is done , but inquisitive minds crave adult perfomance. May Java 7 be with us.

It's time to parallelize

Java 7 provides an excellent API for parallelizing recursive tasks. With its release, one of the additions to the java.util.concurrent packages appeared - the implementation of the Divide and Conquer paradigm - Fork-Join. The idea is this: recursively break the task into subtasks, solve, and then combine the results. More details on this technology can be found in the documentation .

Let's see how easily and effectively this paradigm can be applied to our Strassen algorithm.

Climax

You probably are already eager to look at comparing the performance of algorithms on real hardware. Immediately stipulate that we will conduct testing on square matrices. So we have:

1. The traditional (Cubic) matrix multiplication method
2. Traditional using transpose
3. Strassen Algorithm
4. Parallel Strassen Algorithm

The dimension of the matrices will be set in the interval [100..4000] and in increments of 100.



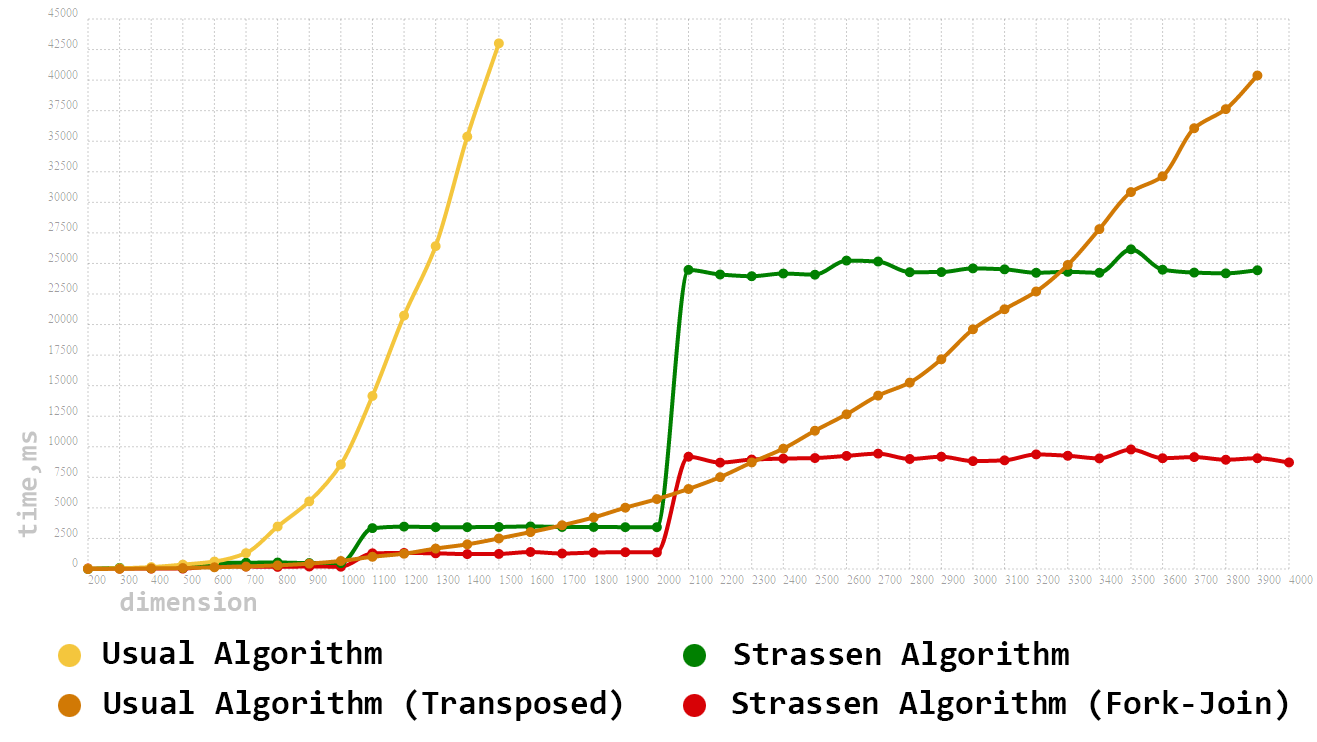
As expected, our first algorithm immediately fell out of the top three. But with his modernized brother (the transpose option), things are not so simple. Even at fairly large dimensions, this algorithm is not only inferior, but often superior to the single-threaded Strassen algorithm. And yet, having a trump card in the form of a Fork-Join Framework, we managed to get a significant performance boost. Parallelization of the Strassen algorithm allowed us to reduce the multiplication time by almost 3 times, as well as to lead our final total.

»Source code posted here .

We welcome feedback and comments on our work. Thanks for attention!