ClusterR ClusterR Part 1
- Transfer
- Tutorial
This article is about clustering, or rather, my recently added ClusterR package in CRAN . Details and examples below are mostly based on the Vignette package.
Cluster analysis or clustering is the task of grouping a set of objects in such a way that the objects within one group (called a cluster) are more similar (in one sense or another) to each other than to objects in other groups (clusters). This is one of the main tasks of research data analysis and the standard statistical analysis technique used in various fields, including machine learning, pattern recognition, image analysis, information retrieval, bioinformatics, data compression, computer graphics.
The most famous examples of clustering algorithms areconnectivity-based clustering (hierarchical clustering), center-based clustering (k-means method, k-medoid method), distribution-based clustering (GMM - Gaussian mixture models) and density-based clustering (DBSCAN - Density- based spatial clustering of applications with noise - spatial clustering of applications with noise based on density, OPTICS - Ordering points to identify the clustering structure - ordering points to determine the clustering structure, etc.).
The ClusterR package consists of center-based clustering algorithms (k-means method, k-means in mini-groups, k-medoids) and distributions (GMM). The package also offers functions for:
Gaussian mixture of distributions - a statistical model for representing normally distributed subpopulations within a general population. A Gaussian mixture of distributions is parameterized by two types of values - a mixture of component weights and average components or covariances (for the multidimensional case). If the number of components is known, the technique most often used to evaluate the parameters of the distribution mixture is the EM algorithm.
The GMM function in the ClusterR package is an implementation on the R class for modeling data as a Gaussian mixture of distributions (GMM) from the Armadillo library with the assumption of diagonalcovariance matrices. You can configure the parameters of the function, including gaussian_comps , dist_mode (eucl_dist, maha_dist), seed_mode (static_subset, random_subset, static_spread, random_spread), km_iter and em_iter (more information about the parameters in the package documentation). I will illustrate the GMM function on synthetic data dietary_survey_IBS .
Initially, the GMM function returns centroids , the covariance matrix (where each row represents a diagonal covariance matrix), weights and logarithmic likelihood functions for each Gaussian component. The predict_GMM function then takes the GMM model output and returns the probable clusters.
In addition to the functions already mentioned, Optimal_Clusters_GMM can be used to estimate the number of data clusters using either the Akaike information criterion (AIC) or the Bayesian information criterion (BIC).
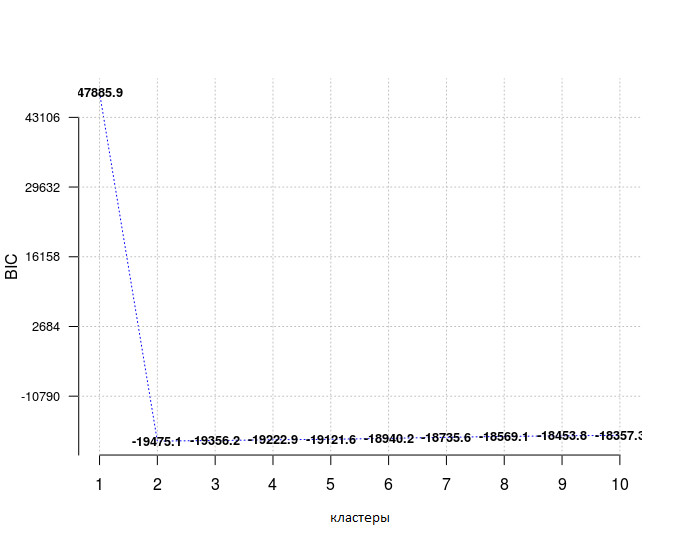
When choosing a model from a predefined set, it is preferable to choose the one with the lowest BIC , here it is true for the number of clusters equal to 2.
Assuming that truth labels are available, you can use the external_validation methods ( rand_index, adjusted_rand_index, jaccard_index, fowlkes_Mallows_index, mirkin_metric, purity, entropy, nmi (normalized mutual information) and var_info (variation of information).
And if the summary_stats parameter is set to TRUE, then metrics of specificity, sensitivity, accuracy, completeness, and F-measure are also returned ( specificity, sensitivity, precision, recall, F-measure, respectively).
K-Means Clustering , a vector quantization method originally used in signal processing, is often used for cluster data analysis. The purpose of clustering by the k-means method is to divide n values into k clusters in which each value belongs to a cluster with the closest average acting as a prototype of the cluster. This leads to the division of the data region into Voronoi cells . The most commonly used algorithm uses an iterative refinement technique. Due to its widespread use, it is called the k-means algorithm; in particular, among specialists in the field of computer science, it is also known as the Lloyd algorithm .
The ClusterR package provides two different k-means functions,KMeans_arma , a R implementation of the k-means method from the armadillo library, and KMeans_rcpp , which uses the RcppArmadillo package. Both functions produce the same results, however, return different symptoms (the code below illustrates this).
KMeans_arma is faster than the KMeans_rcpp function, however, initially it only displays the centroids of some clusters. Moreover, the number of columns in the data must exceed the number of clusters, otherwise the function will return an error. Clustering will work faster on multi-core machines with OpenMP enabled (e.g. -fopenmp in GCC). The algorithm is initialized once, and usually 10 iterations are enough for convergence. The original centroids are distributed using one of the algorithms - keep_existing, static_subset, random_subset, static_spread or random_spread . If seed_mode is keep_existing, the user must pass a centroid matrix to the input.
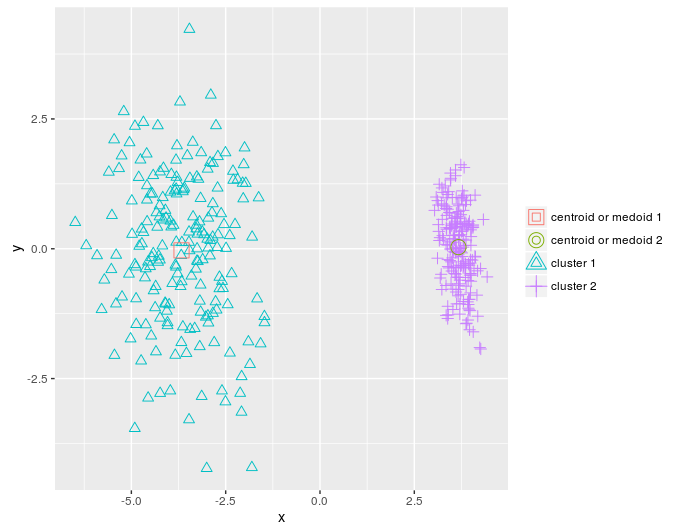
I will reduce the number of measurements in the dietary_survey_IBS data using principal component analysis (PCA), namely the princomp function from the stats package , so that a two-dimensional graph of the clusters constructed as a result can be derived.
As stated above, the KMeans_rcpp function offers some additional features compared to the KMeans_arma function :
More details about KMeans_rcpp are in the package documentation. I will illustrate the different parameters of KMeans_rcpp using the example of vector quantization and the OpenImageR package.

The between.SS_DIV_total.SS attribute is (total_SSE - sum (WCSS_per_cluster)) / total_SSE . If there is no pattern in clustering, the intermediate sum of squares will be a very small part of the total sum of squares, and if the between.SS_DIV_total.SS attribute is close to 1.0, the values are clustered quite well.

In addition, you can use the Optimal_Clusters_KMeans function (which implicitly uses KMeans_rcpp) to determine the optimal number of clusters. The criteria available are variance_explained, WCSSE (within-cluster-sum-of-squared-error), dissimilarity, silhouette, distortion_fK, AIC, BIC and Adjusted_Rsquared . The package documentation has more information for each criterion.
The following code example uses the distortion_fK criterion , which is fully described in the article “Selection of K in K-means clustering, Pham., Dimov., Nguyen., (2004)” (“Choosing K in K-means clustering”).
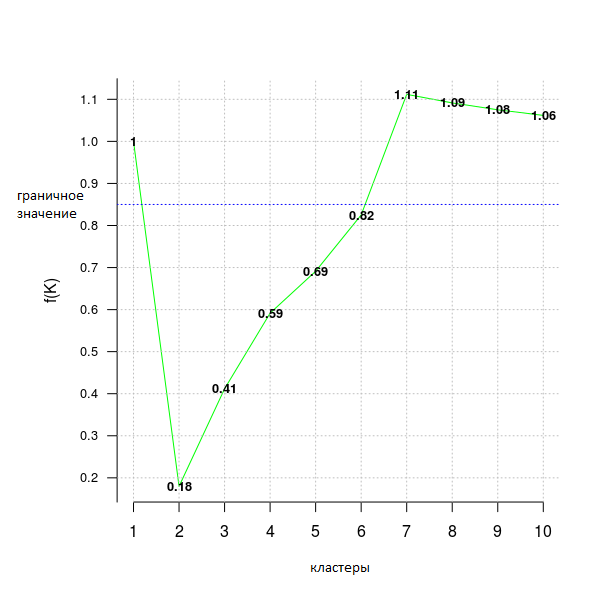
Values less than the fixed border (here fK_threshold = 0.85) can be recommended for clustering. However, there is more than one optimal partitioning into clusters, therefore f (K) should be used only for the assumption of their number, but the final decision whether to accept this value or not is up to the user.
The k-means method in mini-groups is a variation of the classical k-means algorithm. It is especially useful for large data sets, because instead of using the entire set (as in k-means), mini-groups of random data values are taken to optimize the objective function.
The parameters of the MiniBatchKmeans algorithm are almost the same as the KMeans_rcpp functions from the ClusterR package. The most important difference is the batch_size parameter (the size of mini-groups) and init_fraction (the percentage of data for determining the initial centroids, which is used if the initializer is equal to 'kmeans ++' or 'quantile_init').
I will use an example of vector quantizationto show the difference in calculation time and output quality of the KMeans_rcpp and MiniBatchKmeans functions.

First we perform k-means clustering .

Now clustering k-means in mini-groups .

Despite the small difference in the quality of output, k-means in mini-groups returns an average of two times faster than the classical k-means method for this data set.
To implement the k-means method in mini-groups, I used the following resources:
Cluster analysis or clustering is the task of grouping a set of objects in such a way that the objects within one group (called a cluster) are more similar (in one sense or another) to each other than to objects in other groups (clusters). This is one of the main tasks of research data analysis and the standard statistical analysis technique used in various fields, including machine learning, pattern recognition, image analysis, information retrieval, bioinformatics, data compression, computer graphics.
The most famous examples of clustering algorithms areconnectivity-based clustering (hierarchical clustering), center-based clustering (k-means method, k-medoid method), distribution-based clustering (GMM - Gaussian mixture models) and density-based clustering (DBSCAN - Density- based spatial clustering of applications with noise - spatial clustering of applications with noise based on density, OPTICS - Ordering points to identify the clustering structure - ordering points to determine the clustering structure, etc.).
The ClusterR package consists of center-based clustering algorithms (k-means method, k-means in mini-groups, k-medoids) and distributions (GMM). The package also offers functions for:
- validation of output using truth labels;
- outputting results on a contour or two-dimensional graph;
- predictions of new observational results;
- Estimates of the optimal number of clusters for each individual algorithm.
Gaussian mixture of distributions (GMM - Gaussian mixture models)
Gaussian mixture of distributions - a statistical model for representing normally distributed subpopulations within a general population. A Gaussian mixture of distributions is parameterized by two types of values - a mixture of component weights and average components or covariances (for the multidimensional case). If the number of components is known, the technique most often used to evaluate the parameters of the distribution mixture is the EM algorithm.
The GMM function in the ClusterR package is an implementation on the R class for modeling data as a Gaussian mixture of distributions (GMM) from the Armadillo library with the assumption of diagonalcovariance matrices. You can configure the parameters of the function, including gaussian_comps , dist_mode (eucl_dist, maha_dist), seed_mode (static_subset, random_subset, static_spread, random_spread), km_iter and em_iter (more information about the parameters in the package documentation). I will illustrate the GMM function on synthetic data dietary_survey_IBS .
library(ClusterR)
data(dietary_survey_IBS)
dim(dietary_survey_IBS)
## [1] 400 43
X = dietary_survey_IBS[, -ncol(dietary_survey_IBS)] # данные (без зависимой переменной)
y = dietary_survey_IBS[, ncol(dietary_survey_IBS)] # зависимая переменная
dat = center_scale(X, mean_center = T, sd_scale = T) # центрирование и масштабирование данных
gmm = GMM(dat, 2, dist_mode = "maha_dist", seed_mode = "random_subset", km_iter = 10,
em_iter = 10, verbose = F)
# предсказание центроидов, ковариационной матрицы и весов
pr = predict_GMM(dat, gmm$centroids, gmm$covariance_matrices, gmm$weights)
Initially, the GMM function returns centroids , the covariance matrix (where each row represents a diagonal covariance matrix), weights and logarithmic likelihood functions for each Gaussian component. The predict_GMM function then takes the GMM model output and returns the probable clusters.
In addition to the functions already mentioned, Optimal_Clusters_GMM can be used to estimate the number of data clusters using either the Akaike information criterion (AIC) or the Bayesian information criterion (BIC).
opt_gmm = Optimal_Clusters_GMM(dat, max_clusters = 10, criterion = "BIC",
dist_mode = "maha_dist", seed_mode = "random_subset",
km_iter = 10, em_iter = 10, var_floor = 1e-10,
plot_data = T)
When choosing a model from a predefined set, it is preferable to choose the one with the lowest BIC , here it is true for the number of clusters equal to 2.
Assuming that truth labels are available, you can use the external_validation methods ( rand_index, adjusted_rand_index, jaccard_index, fowlkes_Mallows_index, mirkin_metric, purity, entropy, nmi (normalized mutual information) and var_info (variation of information).
res = external_validation(dietary_survey_IBS$class, pr$cluster_labels,
method = "adjusted_rand_index", summary_stats = T)
res##
## ----------------------------------------
## purity : 1
## entropy : 0
## normalized mutual information : 1
## variation of information : 0
## ----------------------------------------
## specificity : 1
## sensitivity : 1
## precision : 1
## recall : 1
## F-measure : 1
## ----------------------------------------
## accuracy OR rand-index : 1
## adjusted-rand-index : 1
## jaccard-index : 1
## fowlkes-mallows-index : 1
## mirkin-metric : 0
## ----------------------------------------
And if the summary_stats parameter is set to TRUE, then metrics of specificity, sensitivity, accuracy, completeness, and F-measure are also returned ( specificity, sensitivity, precision, recall, F-measure, respectively).
K-means method
K-Means Clustering , a vector quantization method originally used in signal processing, is often used for cluster data analysis. The purpose of clustering by the k-means method is to divide n values into k clusters in which each value belongs to a cluster with the closest average acting as a prototype of the cluster. This leads to the division of the data region into Voronoi cells . The most commonly used algorithm uses an iterative refinement technique. Due to its widespread use, it is called the k-means algorithm; in particular, among specialists in the field of computer science, it is also known as the Lloyd algorithm .
The ClusterR package provides two different k-means functions,KMeans_arma , a R implementation of the k-means method from the armadillo library, and KMeans_rcpp , which uses the RcppArmadillo package. Both functions produce the same results, however, return different symptoms (the code below illustrates this).
KMeans_arma
KMeans_arma is faster than the KMeans_rcpp function, however, initially it only displays the centroids of some clusters. Moreover, the number of columns in the data must exceed the number of clusters, otherwise the function will return an error. Clustering will work faster on multi-core machines with OpenMP enabled (e.g. -fopenmp in GCC). The algorithm is initialized once, and usually 10 iterations are enough for convergence. The original centroids are distributed using one of the algorithms - keep_existing, static_subset, random_subset, static_spread or random_spread . If seed_mode is keep_existing, the user must pass a centroid matrix to the input.
I will reduce the number of measurements in the dietary_survey_IBS data using principal component analysis (PCA), namely the princomp function from the stats package , so that a two-dimensional graph of the clusters constructed as a result can be derived.
pca_dat = stats::princomp(dat)$scores[, 1:2]
km = KMeans_arma(pca_dat, clusters = 2, n_iter = 10, seed_mode = "random_subset",
verbose = T, CENTROIDS = NULL)
pr = predict_KMeans(pca_dat, km)
table(dietary_survey_IBS$class, pr)
class(km) = 'matrix'
plot_2d(data = pca_dat, clusters = as.vector(pr), centroids_medoids = as.matrix(km))
KMeans_rcpp
As stated above, the KMeans_rcpp function offers some additional features compared to the KMeans_arma function :
- it allows more than one initialization (can be parallelized with OpenMP)
- in addition to initializations with optimal_init, quantile_init, random or kmeans ++ , you can specify centroids in the CENTROIDS parameter
- algorithm running time and its convergence can be configured with num_init, max_iters and tol parameters
- if num_init> 1, KMeans_rcpp returns the best initialization attributes using the criteria within-cluster-sum-of-squared-error (sum-squared-error-within-cluster)
- the algorithm returns the following attributes: clusters, fuzzy_clusters (if fuzzy = TRUE), centroids, total_SSE, best_initialization, WCSS_per_cluster, obs_per_cluster, between.SS_DIV_total.SS
More details about KMeans_rcpp are in the package documentation. I will illustrate the different parameters of KMeans_rcpp using the example of vector quantization and the OpenImageR package.
library(OpenImageR)
path = 'elephant.jpg'
im = readImage(path)
# сначала изменим размер картинки, чтобы уменьшить количество измерений
im = resizeImage(im, 75, 75, method = 'bilinear')
imageShow(im) # вывод исходного изображения
im2 = apply(im, 3, as.vector) # векторизированный RGB 
# кластеризация с KMeans_rcpp
km_rc = KMeans_rcpp(im2, clusters = 5, num_init = 5, max_iters = 100,
initializer = 'optimal_init', threads = 1, verbose = F)
km_rc$between.SS_DIV_total.SS
## [1] 0.9873009
The between.SS_DIV_total.SS attribute is (total_SSE - sum (WCSS_per_cluster)) / total_SSE . If there is no pattern in clustering, the intermediate sum of squares will be a very small part of the total sum of squares, and if the between.SS_DIV_total.SS attribute is close to 1.0, the values are clustered quite well.
getcent = km_rc$centroids
getclust = km_rc$clusters
new_im = getcent[getclust, ] # каждое значение ассоциируется с ближайшим центроидом
dim(new_im) = c(nrow(im), ncol(im), 3) # обратное преобразование к трехмерной картинке
imageShow(new_im)

In addition, you can use the Optimal_Clusters_KMeans function (which implicitly uses KMeans_rcpp) to determine the optimal number of clusters. The criteria available are variance_explained, WCSSE (within-cluster-sum-of-squared-error), dissimilarity, silhouette, distortion_fK, AIC, BIC and Adjusted_Rsquared . The package documentation has more information for each criterion.
The following code example uses the distortion_fK criterion , which is fully described in the article “Selection of K in K-means clustering, Pham., Dimov., Nguyen., (2004)” (“Choosing K in K-means clustering”).
opt = Optimal_Clusters_KMeans(im2, max_clusters = 10, plot_clusters = T,
verbose = F, criterion = 'distortion_fK', fK_threshold = 0.85)
Values less than the fixed border (here fK_threshold = 0.85) can be recommended for clustering. However, there is more than one optimal partitioning into clusters, therefore f (K) should be used only for the assumption of their number, but the final decision whether to accept this value or not is up to the user.
The k-means method in mini-groups
The k-means method in mini-groups is a variation of the classical k-means algorithm. It is especially useful for large data sets, because instead of using the entire set (as in k-means), mini-groups of random data values are taken to optimize the objective function.
The parameters of the MiniBatchKmeans algorithm are almost the same as the KMeans_rcpp functions from the ClusterR package. The most important difference is the batch_size parameter (the size of mini-groups) and init_fraction (the percentage of data for determining the initial centroids, which is used if the initializer is equal to 'kmeans ++' or 'quantile_init').
I will use an example of vector quantizationto show the difference in calculation time and output quality of the KMeans_rcpp and MiniBatchKmeans functions.
path_d = 'dog.jpg'
im_d = readImage(path_d)
# сначала изменим размер картинки, чтобы уменьшить количество измерений
im_d = resizeImage(im_d, 350, 350, method = 'bilinear')
imageShow(im_d) # вывод исходного изображения
im3 = apply(im_d, 3, as.vector) # векторизированный RGB
dim(im3) # исходные измерения данных# 122500 3
First we perform k-means clustering .
start = Sys.time()
km_init = KMeans_rcpp(im3, clusters = 5, num_init = 5, max_iters = 100,
initializer = 'kmeans++', threads = 1, verbose = F)
end = Sys.time()
t = end - start
cat('time to complete :', t, attributes(t)$units, '\n')
# время выполнения : 2.44029 secs
getcent_init = km_init$centroids
getclust_init = km_init$clusters
new_im_init = getcent_init[getclust_init, ] # каждое значение ассоциируется с ближайшим центроидом
dim(new_im_init) = c(nrow(im_d), ncol(im_d), 3) # обратное преобразование к трехмерной картинке
imageShow(new_im_init)

Now clustering k-means in mini-groups .
start = Sys.time()
km_mb = MiniBatchKmeans(im3, clusters = 5, batch_size = 20, num_init = 5, max_iters = 100,
init_fraction = 0.2, initializer = 'kmeans++', early_stop_iter = 10,
verbose = F)
pr_mb = predict_MBatchKMeans(im3, km_mb$centroids)
end = Sys.time()
t = end - start
cat('time to complete :', t, attributes(t)$units, '\n')
# время выполнения : 0.8346727 secs
getcent_mb = km_mb$centroids
new_im_mb = getcent_mb[pr_mb, ] # каждое значение ассоциируется с ближайшим центроидом
dim(new_im_mb) = c(nrow(im_d), ncol(im_d), 3) # обратное преобразование к трехмерной картинке
imageShow(new_im_mb)

Despite the small difference in the quality of output, k-means in mini-groups returns an average of two times faster than the classical k-means method for this data set.
To implement the k-means method in mini-groups, I used the following resources:
