Why do not blame your problems for inaccuracy of O-ratings

The recent publication of this and this this inspired me to write this post.translations in which authors in an intelligent form express their dissatisfaction with how O-estimates of the computational complexity of seemingly classical algorithms came into dissonance with their practical development experience. The main subject of criticism was the memory model, in the framework of which these estimates were obtained - it, de, does not take into account the peculiarities of the hierarchical organization by the principle of speed, which takes place in modern computing systems. From which all subsequent troubles grow. And judging by the observed reaction of grateful readers, the authors are far from alone in their indignation and desire to "run into" the classics with their O-big ones. So maybe it’s really worth sending to the landfill the stories of the uncles in white coats laid out by them for lamp-wise and thought-provoking cars,


Let's understand.

In the course of the text, I will refer to the second publication and some comments on it. Touched for the living. But for starters, let's just agree on what is understood in the course of this text.

We introduce the definition. Let and be two real functions defined on the set . Then the record means that there is such a positive number that it is true for everyone . Such a designation is called -notation, and O is called the Bachmann symbol, or simply " O- large."

From this definition it immediately has several consequences:

1. If all holds , then"it follows that . In particular, we have that multiplying by a constant does not change the O -valuation.

Simply put, when you multiply the O- expression by a constant, the Bachmann symbol" eats up this constant. "This means that the equal sign in the expression, which includes O -estimate, can not be interpreted as a classic "equality" and the values of such expressions should not be used mathematical operations without any further detail . otherwise, we would get strange things with the following type: . This is a consequence of arbitrary constants, which "hides" behind the symbol Ahman.

2. If limited to , that is, there exists a number such that for allperformed then .

Translating from mathematical into Russian and taking for simplicity the finite interval of the number line, we have the following: if a function on a given interval does not go to infinity, then the most meaningless thing that can be said about it is that it corresponds to O (1) . This does not say anything new about her behavior .


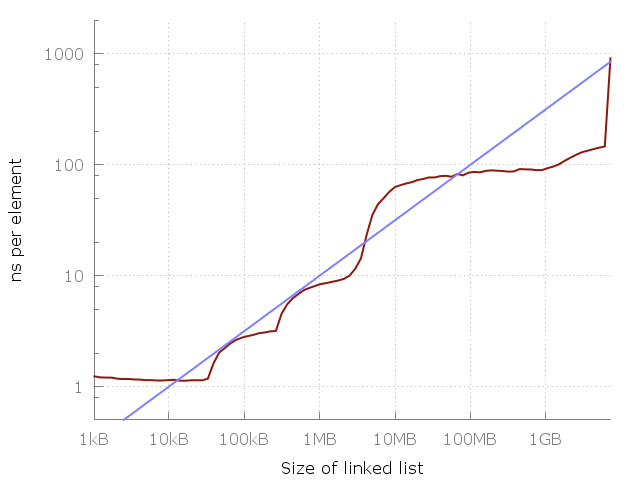
The blue line is O (√N).

Let us return to the case of estimating the complexity of the algorithm and look at the picture provided by the author of the cited publication. Observing an increase in the runtime, a conclusion is made that the estimate O (1) is insolvent. But the interval at which the behavior of the program is analyzed is finite. So in fact it is claimed that the estimate O (1) on it is bad.

Well ... thanks, Cap.

Moreover, further an attempt is made to guess ! the majorizing function is simply in the form of a curve, they say, "looking like it looks." Without conducting any analysis of the algorithm itself, taking into account those features that they are trying to focus on and not introducing any memory model! And why, in fact, is there a square root, and not a cubic one? Or is it not some kind of logarithm? Well, right word, they would offer at least a couple of options, why then immediately "attention, the correct answer"?

It’s worth a reservation here. Naturally, I do not lead to incorrect conclusions that when I switch to a drive “farther” from the processor, the access time drops. But the time of receiving a portion of data for arbitraryaccess to memory, even at the slowest level of the hierarchy, is a constant value, or at least limited. From this the estimate O (1) follows. And if it is not limited and depends on the dimension of the data, then access to the memory is not arbitrary. Well, stupid by definition . Let's not forget that we are dealing with idealized algorithmic constructs. Therefore, when it is said that “data centers will go beyond the HDD” ... Gentlemen, what kind of random access is this, what arrays and hash tables? This is called a swindle under the table: you quietly change the conditions of the task, bring the answer to the previous one and shout: “Ahtung! Wrong how! ” It causes an attack of severe perplexity for me. After all, if the word array , vector or <some type> *your compiler hides, say, a piece of memory distributed over the nodes of a cluster - it can be anything in structure, but not an array in terms of Wirth and Knuth books, and apply the results of formal analysis written in these books to a highly stupid idea. And no less schizophrenia - in all seriousness, talk about the commonality of the assessment, invented by looking at a graph with the results of an arbitrary test.

The fallacy of the given judgment lies in the fact that the O- assessment of complexity is done on the basis of the experiment. To emphasize this, we introduce one more “property” of O -notation, applicable to estimates of algorithmic complexity:

3. O-assessment can be obtained only from the analysis of the structure of the algorithm, but not from the results of the experiment. According to the results of the experiment, it is possible to obtain statistical estimates, expert estimates, approximate estimates and, finally, engineering and aesthetic pleasure - but not asymptotic estimates.

The latter is a consequence of the fact that the very meaning of such estimates is to get an idea of ​​the behavior of the algorithm for sufficiently largedata dimensions, and how large is usually not specified. This is not the only and far from always the main, but interesting characteristic of the algorithm. In the days of Dijkstra and Hoar, orders of dimension 3-6 could be considered large enough, nowadays 10-100 (according to my estimates, which do not pretend to the depth of analysis). In other words, raising the question of obtaining asymptotic estimates of the complexity function of the algorithm, it is convenient to modify the definition of O -notation in this way:

Let . Then it means that there are mutually independent positive numbers A and n , such that for all it holds .

That is, in the analysis of algorithmic complexity, we actually consider majorants of the complexity function on all intervals bounded on the left and not bounded on the right. This means that such O- estimates can be indicated arbitrarily much and all such estimates can be practically useful. Some of them will be accurate for small N , but quickly go to infinity. Others will grow slowly, but they will be fair starting with such N , to which we on our wretched computers like walking to the Moon. So if we assume that the estimate of access time to memoryif any structural analysis is hidden, then this estimate could well be used in a certain range of dimensions, but even then it would not have abolished the fidelity of the estimate O (1).

A classic example of incorrect comparison of asymptotic estimates is square matrix multiplication algorithms. If we make a choice between the algorithms only on the basis of a comparison of the estimates, then we take the Williams algorithm and do not worry. You can only wish creative success to the person who decided to apply it to the matrices of dimensions characteristic of engineering problems. But on the other hand, we know that starting from a certain dimension of the problem, the Strassen algorithm and its various modifications will work faster than the trivial one, and this gives us room for maneuver when choosing approaches to solving the problem.

How stupidity comes from intelligence

Sinning the inaccuracy of O- ratings means completely not understanding the meaning of these estimates, and if so, then no one forces them to use. It is quite possible and often justified to prefer statistical estimates obtained as a result of tests on data sets specific to your area. The illiterate use of such a delicate instrument as asymptotic analysis leads to excesses and generally surprising things. For example, using O -notation, you can "" "prove" "" the inconsistency of the idea of ​​parallel programming.

Suppose that our algorithm, which is fed a chunk of data of dimension N and which is complex when sequentially executed , is easily and unconstrained into the same Nindependent and for simplicity, parts of the same computational and temporal complexity. We get that the complexity of each such part is . Suppose we have M independent calculators. Then the overall complexity of executing a parallel algorithm is nothing but. It turned out that the asymptotic estimate of the complexity of the algorithm does not change as a result of even perfect parallelization to a finite number of processes. But the attentive reader noticed that the “hidden” constant, which the Bachmann symbol had been hamming up, had changed. That is, to draw any general conclusions from such an analysis regarding the very idea of ​​parallelization is at least silly. But another extreme is also possible - to forget that the number of processors, of course, and on the basis of an infinite resource of parallelism, state that the evaluation of the "parallel version of the algorithm" is O (1).

To summarize

As a conclusion, you can provide the following attractive novelty statements:

• It cannot be argued that one algorithm is more efficient than another based on a simple comparison of their O- estimates. Such a statement always requires explanation.
  
  
• It is impossible to conclude from the results of performance measurements about the correctness or incorrectness of such estimates - the hidden constant is usually unknown and can be quite large.
  
  
• You can (and sometimes need) talk about algorithms and data structures without using such estimates at all. To do this, just say what specific properties you are interested in.
  
  
• But it’s better to make specific engineering decisions, taking into account, among other things, such characteristics of the algorithms used.

The assertion that the asymptotic estimates are inaccurate, incorrect, or impractical is often hidden by a reluctance to conduct a normal preliminary analysis of the problem posed and an attempt to rely on the name, but not the essence of the abstractions that are dealt with. Speaking about the asymptotic complexity of the algorithm, a competent specialist understands that this is about idealized constructions, keeps in mind the degree of correctness of projecting them onto real "hardware" and never , from the word "generally", takes engineering decisions relying solely on it. O-evaluations are more useful when developing new algorithms and finding fundamental solutions to complex problems and are much less useful when writing and debugging specific programs for a specific hardware. But if you misinterpreted them and didn’t receive at all what your understanding of what you read in smart books promised you, you must admit that this is not a problem for those who have received evidence of these ratings.