Hello wanderers. We, as travelers by our thoughts, and analyzers of our condition, must understand where it’s good, and where else, where exactly we are, I want to attract the attention of readers to this.

How do we add chains of thoughts, sequentially ?, assuming the output of each step, controlling the flow of control and the state of the cells in memory? Or simply describing the problem statement, indicate to the program which particular task is required to be solved, and this is sufficient for drawing up all the programs. Do not turn coding into a stream of commands that will change the internal state of the system, but express the principle as a concept of sorting, it’s not necessary to imagine what the algorithm is hiding there, you just need to get sorted data. No wonder the president of America may mention the bubble, he expresses the idea that he understood something in programming. He just found out that there is a sorting algorithm, and the data in the table, on his desktop, cannot themselves line up in some magical way, in alphabetical order.

This idea, that I am a good attitude to the declarative way of expressing thoughts, and expressing everything by a sequence of commands and transitions between them, seems archaic and outdated to me, because our grandfathers, grandfathers connected wires on the switching panel and received flashing lights, and we have a monitor and voice recognition, as being at this level of evolution, you can still think about following commands ... It seems to me that if you express a program in a logical language, it will look clearer, and it can be done in technology, this was staked back in the 80s.

Well, the introduction was delayed ....

I will try, for a start, to retell the quick sorting mechanism. To sort the list you need to break it into two sub-lists and connect the sorted one sub-list with the other sorted sub-list .

The split operation should be able to turn the list into two sublists, one of which contains all the elements less than the reference, and the second list contains only large elements. Expressing this on Erlang, they write only two lines:

qsort([])->[];
qsort([H|T])->qsort([X||X<-T,X<H])++[H|qsort([X||X<-T,X>=H])].

These are the expressions of the result of the thinking process that interests me.

It is more difficult to present the description of the principle of sorting in the imperative form. How could such an programming method have an advantage, and then how can you not call it, even though there is a B-Place-Plus, even a Fortran. Is it because javascript, and all the trends of lambda functions in the new standards of all languages ​​- this is a confirmation of the inconvenience of algorithmicity.

I will try to conduct an experiment to verify the advantages of one approach and the other, to test them. I will try to show that the declarative record of the definition of sorting and its algorithmic record can be compared in terms of performance and a conclusion can be drawn on how to correctly formulate programs. Maybe this will push programming on the shelf through algorithms and command streams, as simply outdated approaches, which are not at all relevant to use, because it is no less fashionable to express on Haskel or on a campaign. And can not only fe-sharp can give programs a clear and compact look?

I will use Python to demonstrate, since it has several paradigms, and this is not C ++ at all and no longer lisp. You can write a clear program in a different paradigm:

Sort 1

defqsort(S):if S==[]:return []
    H,T=S[0],S[1:]
    return qsort([X for X in T if X<T])+[H]+qsort([X for X in T if X>=T]) 

Words can be pronounced like this: sorting takes the first element as the base element, and then all the smaller ones are sorted and combined with all the larger elements sorted before .
Or maybe such an expression works faster than sorting written in a clumsy form of rearrangement of some kind, adjacent elements or not. Is it possible to express it more concisely, and require not so many words for this? Try to formulate out loud the principle of bubble sorting and present it to the President of the United States , because that is how he got these sacred data, he learned about the algorithms and put it, for example, like this:In order to sort the list, you need to take a couple of elements, compare them with each other and if the first is more than the second, then you need to swap them, rearrange them, and then you need to repeat the search for pairs of such elements from the very beginning of the list until the permutations end .

Yes, the bubble sorting principle even sounds longer than the quick sort version, but the second advantage is not only in the brevity of the record, but also in its speed, the expression of the same quick sort, formulated by the algorithm, will it be faster than the version that is declaratively expressed? It may be necessary to change the views on learning programming, it is necessary as the Japanese tried to introduce in schools the teaching of Prolog and related thinking. You can systematically move to the removal of algorithmic languages ​​of expression.

Sort 2

To reproduce this, I had to turn to the literature , this is a formulation from Hoare , I try to turn it into a Python:

defquicksort(A, lo, hi):if lo < hi:
        p = partition(A, lo, hi)
        quicksort(A, lo, p - 1)
        quicksort(A, p + 1, hi)
    return A
defpartition(A, lo, hi):
    pivot = A[lo]
    i = lo - 1
    j = hi + 1whileTrue
        do: i= i + 1while A[i] < pivot
        do : j= j - 1while A[j] > pivot
        if i >= j: return j
        A[i],A[j]=A[j],A[i]

I admire the thought, I need an endless cycle, he would have put in a go-that)), there were jokers.

Analysis

Now we will make a long list and make it sort by both methods, and we will understand how faster and more efficiently to express our thoughts. Which approach is easier to perceive?
Creating a list of random numbers as a separate problem , so it can be expressed:

defqsort(S):if S==[]:return []
    H,T=S[0],S[1:]
    return qsort([X for X in T if X<H])+[H]+qsort([X for X in T if X>=H]) 
import random
deftest(len): 
    list=[random.randint(-100, 100) for r in range(0,len)]
    from time import monotonic
    start = monotonic()
    slist=qsort(list)
    print('qsort='+str(monotonic() - start))
    ##print(slist)

Here are the measurements obtained:

>>> test(10000)
qsort=0.046999999998661224
>>> test(10000)
qsort=0.0629999999946449
>>> test(10000)
qsort=0.046999999998661224
>>> test(100000)
qsort=4.0789999999979045
>>> test(100000)
qsort=3.6560000000026776
>>> test(100000)
qsort=3.7340000000040163
>>> 

Now I repeat this in the formulation of the algorithm:

defquicksort(A, lo, hi):if lo < hi:
        p = partition(A, lo, hi)
        quicksort(A, lo, p )
        quicksort(A, p + 1, hi)
    return A
defpartition(A, lo, hi):
    pivot = A[lo]
    i = lo-1 
    j = hi+1whileTrue:
        whileTrue:
            i=i+1if(A[i]>=pivot) or (i>=hi): breakwhileTrue:
            j=j-1if(A[j]<=pivot) or (j<=lo): breakif i >= j: return max(j,lo)
        A[i],A[j]=A[j],A[i]
import random
deftest(len): 
    list=[random.randint(-100, 100) for r in range(0,len)]
    from time import monotonic
    start = monotonic()
    slist=quicksort(list,0,len-1)
    print('quicksort='+str(monotonic() - start))

It was necessary to work on the transformation of the original example of the algorithm from ancient sources in Wikipedia. It means this: you need to take the supporting element and position the elements in the sub-array so that the left is less and the right is more and more. To do this, swap the left with the right element. We repeat this for each sub-list of the supporting element divided by the index, if we have nothing to change to finish .

Total

Let's see what the time difference will be for the same list, which is sorted by two methods in turn. Let's carry out 100 experiments, and let us build a schedule:

import random
deftest(len):
    t1,t2=[],[]
    for n in range(1,100):
        list=[random.randint(-100, 100) for r in range(0,len)]
        list2=list[:]
        from time import monotonic
        start = monotonic()
        slist=qsort(list)
        t1+=[monotonic() - start]
        #print('qsort='+str(monotonic() - start))
        start = monotonic()
        slist=quicksort(list2,0,len-1)
        t2+=[monotonic() - start]
        #print('quicksort='+str(monotonic() - start))import matplotlib.pyplot as plt
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.plot(range(1,100),t1,label='qsort')
    ax.plot(range(1,100),t2,label='quicksort')
    ax.legend()
    ax.grid(True)
    plt.show()
test(10000)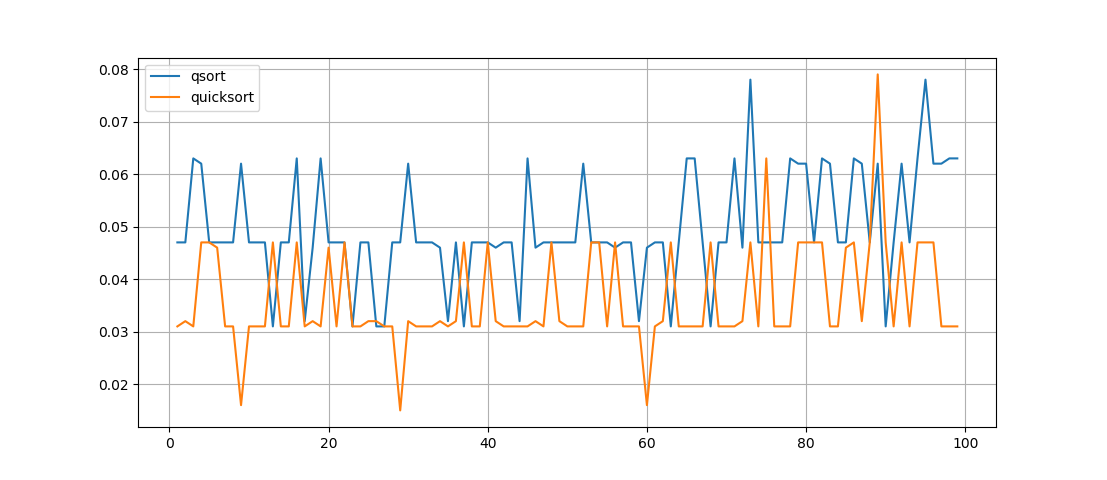

What is seen here is that the quicksort () function works faster , but its recording is not so visual, although the function is recursive, but it’s not at all easy to understand the work of the permutations made in it.

Well, what sort of expression of thought is more aware?

With a small difference in performance, we get such a difference in the volume and complexity of the code.

Maybe the truth is enough to learn imperative languages, and what is more attractive for you?

Ps. And here is the Prologue:

qsort([],[]).
qsort([H|T],Res):-
   findall(X,(member(X,T),X<H),L1), findall(X,(member(X,T),X>=H),L2),
   qsort(L1,S1), qsort(L2,S2),
   append(S1,[H|S2],Res).