What is space-time really?

Translation of Stephen Wolfram's post " What Is Spacetime, Really? "
I express my deep gratitude to Kirill Guzenko KirillGuzenko for help in translating and preparing the publication.

Note: this post by Stephen Wolfram is inextricably linked with the theory of cellular automata and other related concepts, as well as with his book A New Kind of Science , to which a large number of references go from this article. The post illustrates well the application of programming in the scientific field, in particular, Stephen shows (the code is given in the book) many examples of programming in the Wolfram Language in the fields of physics, mathematics, computability theory, discrete systems, etc.

---

Content

A simple theory of everything?
Data structure of the universe.
Space as a graph.
Maybe there is nothing but space.
What is time?
Network formation
Conclusion of SRT
Conclusion of GR (General Relativity)
Particles, quantum mechanics, etc.
In search of the universe
OK, show me the Universe
Engage in physics or not - that is the question
What is required?
But is it time?

---

One hundred years ago, Albert Einstein published the general theory of relativity - a brilliant, elegant theory that survived a century and opened the only successful way to describe space-time ( space-time continuum ).

There are many different points in theory that indicate that the general theory of relativity is not the last point in the history of space-time. And in fact, let me like GR as an abstract theory, but I came to the conclusion that it may have taken us a whole century away from the path of knowing the true nature of space and time.

I thought about the structure of space and time for a little over forty years. In the beginning, as a young theoretical physicist,I just accepted the Einstein mathematical formulation of the problem of the special and general theory of relativity, and also did some work in quantum field theory, cosmology and other fields, based on it.

But about 35 years ago, partly inspired by my experience in technical fields, I began to study in more detail the fundamental issues of theoretical science, which began my long way of going beyond the framework of traditional mathematical equations and using instead of them calculations and programs as the main models in science. Shortly afterwards, I was able to find out that even very simple programs can exhibit very complex behavior, and then, years later, I discovered that systems of any kindmay be presented in terms of these programs.

Inspired by this success, I began to reflect on whether this could be related to the most important of scientific issues - the physical theory of everything.

Firstly, this approach did not seem very promising, if only because the models I studied (cellular automata) seemed to work in such a way that it completely contradicted everything that I knew from physics. But somewhere in the 88th year - at the time when the first version of Mathematica was released , I began to realize that if I changed my ideas about space and time, perhaps this would lead me to something.

A simple theory of everything?

From the article it does not seem at all obvious that the theory of everything for our universe should be simple. And in fact, the history of physics introduces additional doubts, because the more we learn, the more complicated things will be, in any case, in terms of the mathematical apparatus introduced by them. But, as noted, for example, by theologians many centuries ago, there is an obvious feature of our universe - it has order. Particles of our universe not only obey some of their laws, but also obey a certain set of general laws.

But how simple can the theory of everything be for our universe? Say we can present it as a program, say, in Wolfram Language. How big will this program be? Will it be comparable with the length of the human genome, or is it more like the volume of the operating system? Or will it be much smaller?

If I answered this question before I started exploring the computational universe of simple programs, I would most likely answer that such a program must be something very complicated. However, I managed to find that in the computing universe even extremely simple programs can exhibit arbitrarily complex behavior (this fact is reflected in the general principle of computational equivalence ).

Universe Data Structure

But what should be such a program? One thing is clear : if the program can really be extremely simple, then it will be too small to explicitly encode some obvious features of our Universe, such as masses of particles, various kinds of symmetry, or even spatial dimension. All of these things must appear in some way from something lower level and fundamental.

But if the behavior of the universe is determined by a simple program, then what is the data structure with which this program works? At first, I suggested that it should be something simple to describe, such as, for example, the structure of cells that appears in a cellular automaton. But even if such a structure works well for describing models of various thingsIt seems that it should be very implausible for fundamental physical models. Yes, you can find rules that will exhibit behavior that on a large scale will not show the obvious properties of the structure. However, if physics can really be described by some simple model, then it seems that such a rigid structure for space cannot be included in it, and that the properties of space must stem from something.

So what is the alternative? We will needa lower level concept than the space from which it will be born. We also need a basic data structure that will be as flexible as possible. I thought about this for many years, studying the most diverse computational and mathematical formal systems. But in the end, I realized that in fact everything that I came across could be represented in one way - through networks.

A network — a graph — consists of a number of nodes that are connected by links. And all the properties of the graph follow from the structure of these connections.

Space as a graph

So can space consist of something like that ? In classical physics and general relativity, space is not represented as consisting of anything. It is presented in the form of some mathematical construction, which serves as something like a scene on which there is a continuous range of possible positions occupied by different objects.

However, can we say for sure that space is continuous? When quantum mechanics arose, it was popularthe idea that space, like everything else, is quantized. But it was not clear how this idea could be combined with SRT, in fact, there was no clear evidence of the discreteness of space. When I started to study physics in the seventies, the discussion of the discreteness of space came to naught, plus it was experimentally proved that discreteness was not observed on scales up to 10 ^-18 m (1/1000 proton radius, or attometer ). After 40 years and tens of billions of dollars spent on particle accelerators on a scale of 10 ^-22 m (or 100 yo-meters ), the discreteness of space was not found.

However, there is an opinion that it should manifest itself on a scale near the Planck length - 10 ^-34meter. But when people think about it , say, in the context of spin networks, loop gravity, or whatever you are, they tend to assume that everything that happens there is closely related to formalisms and concepts of quantum mechanics.

But what if space - probably on a Planck scale - is only a good old graph devoid of quantum properties? It doesn’t sound very impressive, but much less information is required to set up such a graph - just tell which nodes are connected to which.

But how can this create space? First of all, where does the apparent continuity of space come from on a large scale? In fact, everything is very simple: this may be the result of a large number of nodes and connections. A bit likewhat happens in liquids - say, in water. On a small scale, we can observe molecules rushing about in thermal motion. However, the large-scale effect causes all these molecules to generate what we perceive as a continuous liquid.

It so happened that in the mid-80s I spent a lot of time studying this phenomenon - this was part of my work, in which I understood the nature of the seeming randomness of turbulent fluid flows . In particular, I was able to show that if we imagine molecules as cells of a cellular automaton, then their large-scale behavior will be accurately described by differential equations for fluid flows.



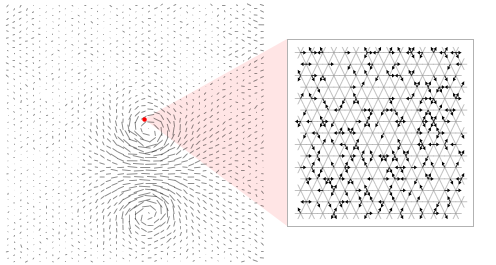
And therefore, when I began to think about the possibility of the existence of a substructure of space that can be represented in the form of a network, I thought that the same methods could be used here and that this could reduce Einstein's equations of general relativity to other, much lower-level ones.

Maybe there is nothing but space

Good. Let's say space is a network. But what about all the things located in space? What about electrons, quarks, protons and more? Standard physical concepts indicate that space is the scene on which particles, strings, or whatever. However, such a representation becomes very complex. But there is a simpler option: perhaps everything in our universe consists of space.

In the last years of his life, Einstein was very passionate about this idea . He believed that, perhaps, particles such as electrons can be considered as something like black holes that consist of only one space. However, relying only on the formalism of general relativity, Einstein could not develop this idea, as a result of which it was abandoned.

And, it so happened that a hundred years before that, similar ideas lived in the minds of some people. These were the days before the SRT, when people thought that space was filled with a medium similar to liquid - ether (ironically, at the present time we have returned to the model of filled space - the Higgs field , quantum fluctuations in a vacuum, etc.). Meanwhile, it was clear that there are different types of atoms corresponding to different chemical elements. And it was suggested (in particular, by Kelvin ) that different nodes of the ether can be associated with different atoms . This is an interesting idea, albeit a wrong one. But, representing space as a network, we can consider a similar idea: it is possible that particles correspond to certain network structures



. Perhaps everything in the universe is a network, and some structures of this network correspond to matter. Such things can easily be found on the field of a cellular automaton. Even if each cell obeys some simple rules, certain structures appear in the system with their own properties - just like particles with the physics of interaction with each other. How all this can be implemented on networks is a separate and very big topic. However, first we should discuss one very important thing - time.

What time is it?

In the 19th century there were concepts of space and time. Both were described by coordinates, and using some mathematical formalisms they appeared in a similar way. However, the idea that space and time are in some way the same thing was not in use. But then Einstein appeared with general relativity, and people began to talk about space-time , in which space and time are the facets of a single concept.

It makes a lot of sense in STR, in which, for example, moving with variable speed is the essence of rotation in four-dimensional space-time. And throughout this century, physicists have considered space-time as a kind of entity in which space and time have no fundamental differences.

But how will it all bework in the context of a network model of space? Of course, you can introduce a four-dimensional network in which time will work in the same way as space. And then just say that our universe corresponds to some space-time network (or family of networks). Each network should be determined by some restrictions: our universe has such and such properties, and, it turns out, satisfies such and such equations. However, this seems to be a non-constructive approach - it does not talk about how the universe behaves, but only that if something has such-and-such behavior, then this can be something in the universe.

And, for example, in the context of programs, space and time manifest themselves in very different ways. In cellular automata, for example, cells are located in space, however, the behavior of the system occurs in incremental changes in time. But here is the point: from the fact that low-level rules strongly distinguish between the behavior of space and time, it does not follow that on a large scale they will not behave in a similar way - as it should be in modern physics.

Network formation

So, let's assume that the network is a subspace structure. How is this network formed ? You can introduce a simple hypothesis, which is that there is some local rule that says that if you see some fragment of the network that looks in some way, then you should replace it with a fragment that looks like this. But now it’s getting a little more complicated. After all, there can be many places on the network where you can apply a similar rule. So what determines the processing order of each fragment? In fact, every possible ordering corresponds to its time stream. And one could imagine a theory in which all flows have a place to be, and our universe has a multiple history .







But we can do without this hypothesis. Instead, it is quite possible that there is only one thread of time - and this correlates well with what we know about the world, with our experience. And in order to understand this, we should do something like what Einstein did in formulating STO: we should introduce a more realistic model of what an observer can be.

Needless to say, some real observer must be able to exist in our universe. Thus, if the universe is a network, then the observer should be some part of this network. Recall now about the constant small changes that occur in the network. In order to know that such a change (update) has occurred, the observer himself must be changed (updated).

If youif you go through all this mental chain that I spent in A New Kind of Science (NKS), you will understand that the only thing that observers can perceive in the history of the universe - the causal network - is when one event triggers another.

And then it turns out that there is a certain class of basic rules for which different orders of basic updates do not affect the causal network. I call them “causally invariant” rules.

Causal invariance is an interesting property that has analoguesin various computational and mathematical systems, for example, in that transformations in algebra can be applied in any order and will give the same final result. But in the context of the universe, its consequence is that it guarantees that there is only one stream of time in the universe.

Conclusion STO

So what about spacetime and SRT? Here, as I understood it in the mid-90s, something exciting happens : if there is causal invariance, then it follows that on a large scale, SRT will appear by itself. In other words, even if at the lowest level of space and time, everything happens in a completely different way, then on a larger scale, all this gives rise to what STO prescribes.

Roughly speaking, reference frames in the special theory of relativity - associated, for example, with movements at different speeds - correspond to different sequences of low-level network changes. But due to causal invariance, the general behavior associated with different sequences is obtained in exactly the same way - thus, the system satisfies the principles of STR.

In the beginning, this situation might seem hopeless: how can a network that considers space and time in different ways converge with SRT? But it does work. And in fact, I do not know of any other model that can successfully deduce the principles of SRT from something lower level; in modern physics, this has always been presented as a given.

Conclusion of General Relativity (General Relativity)

Ok, STO can be obtained from simple network-based models. But what about GR? There is very good news: based on various assumptions, in the late 90s I was able to derive Einstein's equations from the dynamics of networks.

This whole story is actually somewhat more complicated, but here is an approximate retelling. First, we should imagine how a network forms a space. It should be remembered that a network is only a set of nodes and links. Moreover, the nodes can be located in one-dimensional, two-dimensional, or any n-dimensional space.

It is easy to see that there are networks that on a large scale appear to be two-dimensional or three-dimensional. In fact, there is a simple test to determine the effective network dimension. Take a node and then look at all the nodes that are r links away from it. If the network manifests itself as d- dimensional, then the number of nodes in this “sphere” will be about r ^d . And here things get an interesting turn. If the network behaves as a d- dimensional space undistorted in a space of a larger dimension , then the number of nodes will always be about r ^d . But if the behavior is like a curved space (as in GR), then there will be a correction term proportional to such a mathematical object as



Ricci tensor . And this is very interesting, because the Ricci tensor just arises in the Einstein equations. There are many mathematical difficulties. The shortest paths should be considered - the geodesic lines of the network. You should understand how to do anything, not only in space, but also on the network over time. It should also be understood to what extent the properties of the network are manifested. When deriving mathematical results, it is important to be able to get all sorts of average values. In fact, this is similar to deriving equations for a liquid from the dynamics of molecules: you need to be able to take the average from a certain range of random values ​​in low-level interactions.







But the good news is that there is an immense number of systems built even on extremely simple rules that are similar to digits of pi , that is, for any applied purposes they are quite random . It turns out that even if the features of the causal network are fully defined for someone who knows the initial state of the network, then most of these features will, in fact, be random.

Here is what we have in the end. If we introduce the assumption of effective microscopic randomness and assume that the behavior of the system as a whole does not lead to a change in all limiting dimensions, then it follows that the scale behavior of the system satisfies Einstein's equations !

I think this is very interesting. Einstein's equations can be obtained from practically nothing. This means that these simple networks reproduce the features of gravity that we know from modern physics.

There are a number of details that do not fit the format of this article. I voiced many of them for quite some time at the NKS , especially in the notes at the end.

Some of the things may be worth mentioning. Firstly, it is worth noting that these basis networks are not only represented in the usual continuously defined space, but also do not define such topological concepts as inside and out. All these concepts are a consequence and deduced.

When it comes to deriving Einstein's equations, Ricci tensors are born from geodesic lines on a network along with the growth of spheres that originate from every point on the geodesic line.

The resulting Einstein equations are Einstein's equations for vacuum. But as in the case of gravitational waves, it is possible to effectively separate the features of space associated with matter, and then obtain the full Einstein equations in terms of matter-energy-momentum.

When I write this, I understand how easily I slip into the "language of physicists" (probably this is due to the fact that I was engaged in physics in my youth ...). But it’s simple enough to say that an exciting thing appears at a high level, which consists in the fact that from the simple idea of ​​networks and cause-effect invariant replacement rules, equations of GR can be derived. Having done surprisingly little, we get a bright star of 20th-century physics: the general theory of relativity.

Particles, quantum mechanics and more

It is great to be able to derive GR. But physics does not end there. Another very important part of it is quantum mechanics . I'm afraid I will not be able to expand this topic in detail within the framework of this article, but, apparently, particles such as electrons, quarks, or Higgs bosons should be represented as some special areas of the network. In a qualitative sense, they may not differ much from the "ether nodes" of Kelvin.

But then their behavior must follow the rules that we know from quantum mechanics - or, more specifically, from quantum field theory. A key feature of quantum mechanics is that it can be formulated in terms of multiple behaviors, each of which is associated with a specific quantum amplitude. I didn’t fully understand all this, but there is a hint that something similar happens if you look at the evolution of the network with various possible sequences of low-level replacements.

My network model, strictly speaking, has no quantum amplitudes. It is more similar (but not exactly) to the classical, in fact, probabilistic model. And for half a century, people believed that practically unsolvable problems were associated with such models. After all, there is Bell’s theorem which says that if there are no instantaneous nonlocal disseminations of information, then there will be no such model of “hidden variables” that can reproduce the quantum-mechanical results observed experimentally.

But there are some fundamental points. It is quite clear to oneself what nonlocality means in ordinary space of a certain dimension. But what can be said in the context of networks? Everything is different here. Because everything is determined by only connections. And although the network may appear to be three-dimensional on a large scale, the possibility remains that there are some “threads” that connect some areas that would be separated from each other without them. And one thought haunts me - there is reason to believe that these threads can be generated by particle-like structures propagating in networks.

In search of the universe

Well, it turns out that some network-based models can reproduce models of modern physics. But where is it worth starting the search for a model that accurately reproduces our universe?

The first thought is to start with existing physics and try to adapt engineering and applied rules so as to reproduce it. But is this the only way? But what if you just start listing all the possible rules, looking among them for those that will describe our universe?

Without starting the study of the computational universe of the simplest programs, I would think that this is a crazy undertaking: the rules of our universe cannot be simple enough to be found by a simple enumeration. But seeing what is happening in the computing universe and seeing some other examples in which amazing thingswere found by brute force alone, I realized that I was wrong.

But what happens if someone really begins to carry out such a search ? Here is a selection of networks obtained after a fairly small number of steps, using all the possible rules of a certain, very simple type: Some of these networks clearly do not correspond to our universe. They simply froze after several iterations, that is, time in them, in fact, stopped. Or the structure of their space was too simple. Or they had an infinite number of dimensions. Or some other problems.





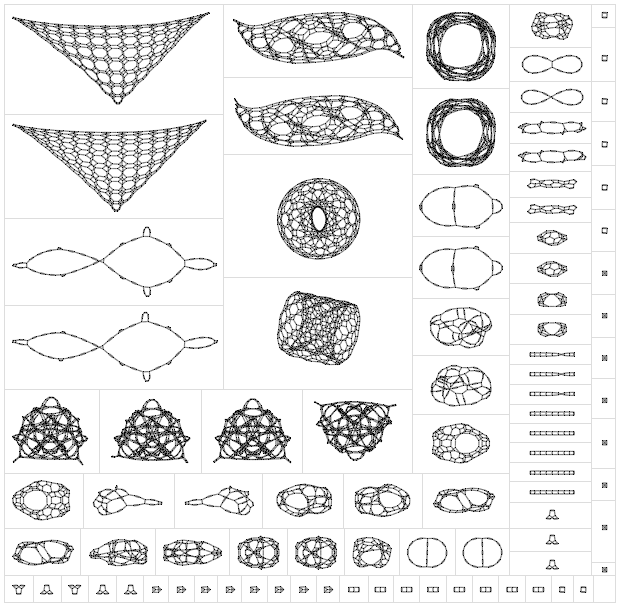
It's great that with such amazing speed we can find those rules that clearly do not correspond to our universe. And to say that it is this object - our universe, is a much more difficult task. Because even if you simulate a large number of steps, it will be incredibly difficult to show that the behavior of this system demonstrates the same thing that physical laws tell us about the early moments of the life of the universe.

Although there are a number of encouraging things. For example, these universes can be born with a virtually infinite number of dimensions, and then gradually shrink to a finite number of dimensions, potentially eliminating the need for explicit inflation in the early Universe.

And if you argue at a higher level, you should remember that if you use very simple models, then there will be a large distance between the “neighboring models”, so most likely, these models will either accurately reproduce the known physical constructions, or will be far from the truth.

In the end, it is necessary to reproduce not only the rules, but also the initial state of the universe. And as soon as we recognize it, we will in principle be able to find out the exact evolution of the universe. So does this mean that you could immediately find out everything about the universe? Definitely not. Because of the phenomenon that I call "computational irreducibility", and which implies that if you know the rules and the initial state for the system, it may still require an irreducible amount of computational work to track each step of the system to find out what it is doing.

However, there is a possibility that someone can find a simple rule and an initial state by saying, “ Look, this is our universe! ” We would find our universe in the space of all possible universes.

Of course, this would be a momentous day for science.

But there would be many other questions. Why exactly this rule, and not another? And why should our universe have a rule that appears early enough in our list of all possible universes, and which we can find by simple enumeration?

One would think that it is precisely the features of our universe and the fact that we are in it that will force us to formulate listing rules so that the universe appears early enough. But at present, I believe that everything should be much more extravagant, as, for example, in the case of an observer in the universe - all of the large class of non-trivial possible rules for universes are actually equivalent, so you can choose any of them and get exactly the same the results are just different.

Ok show me the universe

But all this is just speculation. And until we really find a candidate for the rule of our universe, it’s probably not worth spending a lot of time discussing these things.

So good. What is our current position in all of this? Most of what was being discussed now, I realized somewhere in the 99th - a few years before the end of A New Kind of Science . And although I wrote in a simple language, and not in the format of an article on physics, I managed to cover the main points of this topic in the ninth chapter of the book, adding some technical details in the notes at the end. But after the book was finished in 2002, I started working on physical problems again



. It will be funny to say that there was a computer in my basement that was looking for a fundamental physical theory. But here is what he actually did: he enumerated possible rules of various types and tried to find out if their behavior corresponded to certain criteria that could make them plausible as models of physics.

I did this job very scrupulously, drawing ideas from simple cases, consistently moving towards more realistic ones. There were a lot of technical issues. How to represent large, effectual graph sequences. Or how to quickly recognize subtle patterns that show that a rule does not match our universe.

The work has grown into thousands of pages, if it is presented in print form, gradually bringing it closer to understanding the fundamentals of what networks-based systems can do.



In a way, it was a bit of a hobby that I worked on in parallel with the company management and its technological development . And there was another distraction. For many years I dealt with the problem of computational knowledge and the construction of an engine that could fully implement them. And according to the results of my work on A New Kind of Science, I became convinced that this is possible, and that now is the right time to implement this.

By 2005, it became clear that it was really possible to implement, and therefore I decided to devote myself to this area. The result isWolfram | Alpha . And as soon as Wolfram | Alpha was launched, it became clear that much more could be done - and I devoted my, perhaps, the most productive decade to creating a huge system of ideas and technologies that made it possible to implement Wolfram Language in its current form, and so many other things.

Doing physics or not is the question.

But during this decade I did not study physics. And when I look at the file system on my computer now, I see a large number of laptops with physics materials, grouped with the results I received, and all this has remained abandoned and untouched since the beginning of 2005.

Should I get back to physics? I definitely want this. Although there are other things that I would like to implement.

I spent most of my life working on very large projects. And I worked hard, planning what I was going to do, trying to plan them for the next decade. Sometimes I put off projects because the technologies or infrastructure existing at that time were not ready for them yet. But as soon as I started working on the project, I promised myself to find a way to successfully complete it, even if it would take many years of hard work to implement it.

However, the search for a fundamental physical theory is perhaps somewhat different from the projects that I had to work on earlier. In a sense, the criteria for his success are much tougher: he either solves the problem and finds a theory or not. Yes, one could find many interesting abstract concepts from an emerging theory (as in string theory). And it is likely that such a study will give interesting side results.

But unlike the creation of technology or the study of scientific fields, the formulation of the content of this project is beyond our control. Its content is determined by our universe. And, quite possibly, I'm just mistaken in the assumptions about how our universe works. Or, maybe I’m right, but there is an almost insurmountable barrier due to computational irreducibility, which deprives us of the opportunity to recognize this area.

Someone may say that it is likely that we will find some universe that will resemble ours, but we will never know whether it is ours in reality. I really don't really care about that. I think that there are a sufficient number of anomalies in existing physics attributed to such things as dark matter, the explanation of which will give us complete confidence that we have found the correct theory. It will be great if you can make an assumption and quickly check it. But by the time we deduce all seemingly arbitrary masses of particles, and other known features of physics, we can be sure that we are dealing with the correct theory.

It has been entertaining for many years to ask my friends if I should deal with fundamental questions of physics. And I got three completely different types of answers.

The first one is simple: “ You have to do this! ” They said that the project is the most fascinating and important of those that you can imagine, and they can’t understand why they should wait at least one extra day before embarking on it.

The second type of answer: " Why do you do this?"Then they say something like," Why not solve the problem of artificial intelligence, or molecular engineering, biological immortality, or at least not build a huge multi-billion dollar company? Why do something so abstract and theoretical when you can do something the essential and thereby changing the world? ”

And there is a third type of answer - very expected, given the history of science. It mainly comes from my friends, physicists, and this is a combination of“ Do not waste your time on this! "and" Please do not do this . "

The fact is that the current approach to fundamental physics, based on quantum field theory, has been around for almost 90 years. He had a number of successes, but did not lead us to a fundamental physical theory. But for most modern physicists, the current approach is the essence of physics itself. And when they hear about what I'm working on, it seems to them something so unfamiliar, as if it really is not physics.

And some of my friends just say so: " I hope that you will not succeed, because then everything that I worked on will go down the drain"Well, yes, a lot of what has been done will turn out to be meaningless. But you always face this risk when you are engaged in a project in which nature decides what is right and what is not. But I have to say that even if you can find a truly fundamental physical theory, there will still be a very large field for the work of quantum field theory, for example, an explanation of the various effects on the scales with which we are currently working on particle accelerators.

What is needed?

So, well, if I run a project to find a fundamental physical theory, then what should I do? This is a complex project that will require not only me, but also a diverse group of talented people.

Whether it will ultimately work, I don’t know, but I think it will be quite interesting to watch it, and I plan to present it in a transparent format, making it as accessible and informative as possible (of course, this will be an encouraging contrast with the hermit’s regime in which I have been working on A New Kind of Science for ten years).

Of course, I can’t know how complicated this project is, and whether it will bring any results at all. Ultimately, it depends on what our universe really is. But, based on what I did ten years ago, I have a clear plan for where to start and what kind of people to bring together in one team.

It will require both good scientists and applicants / engineers. It will take a lot of work in the development of algorithms for the evolution of networks and their analysis. I am sure that graph theory, modern geometry, group theory, and, possibly, some other sections of abstract algebra will be required here. And I would not be surprised if as a result a large number of other areas of mathematics and theoretical computer science will be involved.

It will require complex and serious physics, with an understanding of the fundamentals of quantum field theory, string theory and, possibly, such sections as spin networks. It is also likely that methods of statistical physics and its modern theoretical foundations will be required. An understanding of the general theory of relativity and cosmology will be required. And, if things are going well, it will take work on a wide variety of physical experiments, as well as their interpretation.

There will be technical problems - to understand, for example, how to conduct a huge computational work on networks and visualize the results. But I suspect that the biggest problems will be in building a new theory building and understanding what is needed to study the different types of network systems that I want to explore. Support from existing areas will not be superfluous. But in the end, I suspect, it will require the construction of a fundamentally new intellectual structure, which will not be like any of what is available now.

But is it time?

Is the time right now for the implementation of such a project? Maybe you should wait until computers get more computing power. Or when some areas of mathematics go further. Or until answers to a few more questions from physics are received.

I'm not sure. But I do not see any insurmountable obstacles, but only the fact that this project will require efforts and resources. And who knows: maybe this will turn out to be easier than we think, and, looking back, we will wonder why no one has done this before.

One of the key points that led to the general theory of relativity 100 years ago was that the fifth postulate of Euclid(“Parallel lines never intersect”) may not be fulfilled in the real universe, making it possible for curved space to exist. But if my suspicions about the cosmos and the universe are true, then this means that in fact there is a more fundamental problem in the foundations of Euclid - in his very first definitions. Indeed, if there is a discrete subspace network, then Euclid’s assumptions about points and lines that can occupy any spatial position are simply not true.

GR is a great theory, but we already know that it cannot be final. And now we have to wonder how much time will pass before we come to the final theory. Hopefully not too much. And I hope that GTR will not celebrate too many anniversaries before we know what space-time really is.