Generate passwords for Road Rash 1 and 2 games
Recently I saw a post about Road Rash on Habrahabr and I was wondering: "And how is the password system in the other two parts?" I would like to share my observations and results with you in this article.

The password consists of 20 positions, each position consists of 5 bits, total 20 * 5 = 100 bits. These bits store these game parameters:
Now let's see what the raw password consists of:
(U, SN, SN, SN, SN) (U, PC, PC, PC, PC) (U, RF, RF, RF, RF) (U, PD, PD, PD, PD) (U, GV, GV, GV, GV) (H, H, H, H, H) (H, H, H, H, H) (H, H, H, H, H) (H, H , H, H, H) (N, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1 ) (M, M, M, M, C1) (M, M, M, M, C1) (U, U, L, L, L) (U, U, B, B, B) (C2, C2, C2, C2, C2) (C3, C3, C3, C3, C3) (C4, C4, C4, C4, C4)
U - unused bits.
SN - number of the occupied place in Sierra Nevada (0-15) in the binary number system.
PC - number of the occupied place in the Pacific Coast (0-15) in binary system.
RF - number of the occupied place in Redwood Forest (0-15) in binary system.
PD - the number of occupied places in the Palm Desert (0-15) in the binary system.
GV - number of the occupied place in Grass Valey (0-15) in the binary number system.
H - the number of points (0-10485750) in increments = 10. The number of points is divided by 10 and the resulting number is converted to binary.
N is the bit of negative values.
M is the amount of money ((-83886070) -83886070) in steps of = 10.
In order to create a positive amount of money, you need to divide the amount of money by 10 and convert the resulting number into a binary number system.
In order to create a negative amount of money, you need:
L is the level number (1-5) in the binary number system.
B - motorcycle number (0-7) in binary system.
C1 = (sum of positions 1 to 17) mod64 (The resulting number is converted to a binary number system and is mirrored).
C2 = (sum of positions 6 to 10) mod32.
C3 = (sum of positions 11 to 15) mod32.
C4 = C2 XOR C3.
Characters in positions can take the values 0-9 and AV. The bits in the positions are encoded in accordance with the fact that 0 = 00000, 1 = 00001, 2 = 00010 ... U = 11110, V = 11111. That is, it is a simple 5 bit encoding.
The password consists of 8 positions, each position consists of 5 bits, total 8 * 5 = 40 bits. These bits store these game parameters:
Now let's see what the raw password consists of:
(?, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1) (U, U, L, L, L) (B, B, B, B, C1) (T, T, T, T, T) (C2, C2, C2, C2, C2)
? - always equal to zero.
U - unused bits.
M is the amount of money (0-327670) in increments = 10. The amount of money is divided by 10 and the resulting number is converted into a binary system.
L is the level number (1-5) in the binary number system.
B - motorcycle number (0-15) in binary system.
T - traversed tracks (0-5).
The order of bits from high to low:
4 - is responsible for the passage of the fifth trace.
3 - is responsible for the passage of the fourth route.
2 - is responsible for the passage of the third route.
1 - is responsible for the passage of the second route.
0 - is responsible for the passage of the first track.
C1 = (the sum of positions 1 to 6, not counting the 5th position) mod32 (The resulting number is converted to a binary number system and is mirrored).
C2 = ((sum of positions 1 to 6) mod32) XOR 7 position.
The encoding of the values is the same as in the first part.
But that is not all!
I have prepared something else ...
Let's digress a bit from the Sega console and move on to Nes (Dandy). This game very badly ruined my nerves. Who played, he remembers the long questions in Japanese, because of which the passage of the game turns into hell. The passwords in it are simple, but with a subtle emphasis. To complete the game 100% it was necessary to collect 4 armor. But there is one problem, in order to get them, it was necessary to answer a ton of questions. No matter how I delved into the Internet and in my code book, I never found the passwords that save the collected armor. And without them, the final boss will send you far away a ton of Japanese characters. But delving into the assignments of the bits, I found that the game saves:
The password consists of 8 positions, each position consists of 2 bits, total 8 * 2 = 16 bits.
Now let's see what the raw password consists of:
(C, C) (A, L) (L, L) (L, L) (C, C) (G, G) (A, A) (G, G)
C = (the sum of all positions except 1 and 5) in the binary system. The two most significant bits of the checksum are written to the 5th position, and the two least significant bits to the 1 position.
A is the number of armor (0-4) in the binary number system.
L is the level number (0-20) in the binary number system.
G - weapon number (0-15) in the binary system.
For coding, 4 degrees of eating a banana are used, which we denote by numbers:
 = 0
= 0 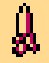 = 1
= 1  = 2
= 2  = 3
= 3
So we went to the finish line.

What would I like to say? Well, I hope this article is useful to someone. Good luck, thanks for reading.

First Road Rash
Theory
The password consists of 20 positions, each position consists of 5 bits, total 20 * 5 = 100 bits. These bits store these game parameters:
- number of the occupied place (0-15) on five different tracks (0 means that you have not traveled on this route yet).
- number of points (0-10485750)
- amount of money ((-83886070) -83886070)
- current level (1-5)
- motorcycle (1-8)
Now let's see what the raw password consists of:
(U, SN, SN, SN, SN) (U, PC, PC, PC, PC) (U, RF, RF, RF, RF) (U, PD, PD, PD, PD) (U, GV, GV, GV, GV) (H, H, H, H, H) (H, H, H, H, H) (H, H, H, H, H) (H, H , H, H, H) (N, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1 ) (M, M, M, M, C1) (M, M, M, M, C1) (U, U, L, L, L) (U, U, B, B, B) (C2, C2, C2, C2, C2) (C3, C3, C3, C3, C3) (C4, C4, C4, C4, C4)
Designations
U - unused bits.
SN - number of the occupied place in Sierra Nevada (0-15) in the binary number system.
PC - number of the occupied place in the Pacific Coast (0-15) in binary system.
RF - number of the occupied place in Redwood Forest (0-15) in binary system.
PD - the number of occupied places in the Palm Desert (0-15) in the binary system.
GV - number of the occupied place in Grass Valey (0-15) in the binary number system.
H - the number of points (0-10485750) in increments = 10. The number of points is divided by 10 and the resulting number is converted to binary.
N is the bit of negative values.
M is the amount of money ((-83886070) -83886070) in steps of = 10.
In order to create a positive amount of money, you need to divide the amount of money by 10 and convert the resulting number into a binary number system.
In order to create a negative amount of money, you need:
- Activate a bit of negative values.
- Subtract the amount of money from the number 83886080 (modulo), divide the resulting balance by 10 and translate the number into binary.
L is the level number (1-5) in the binary number system.
B - motorcycle number (0-7) in binary system.
| Motorcycles | room |
| SHURIKEN 400 | 0 |
| PANDA 600 | 1 |
| BANZAI 750 | 2 |
| KAMIKAZE 750 | 3 |
| SHURIKEN 1000 | 4 |
| FERRUCI 850 | 5 |
| PANDA 750 | 6 |
| DIABLO 1000 | 7 |
C1 = (sum of positions 1 to 17) mod64 (The resulting number is converted to a binary number system and is mirrored).
C2 = (sum of positions 6 to 10) mod32.
C3 = (sum of positions 11 to 15) mod32.
C4 = C2 XOR C3.
Coding
Characters in positions can take the values 0-9 and AV. The bits in the positions are encoded in accordance with the fact that 0 = 00000, 1 = 00001, 2 = 00010 ... U = 11110, V = 11111. That is, it is a simple 5 bit encoding.
Example of generating a password with a positive amount of money
Create a password that saves these parameters:
5 = 0101
3 = 0011
7 = 0111
9 = 1001
1 = 0001
10341950 points / 10 = 1034195 = 11111100011111010011
23915840 money / 10 = 2391584 = 1001000111111000100000
level 5 = 101
motorcycle number 6 = 110
(00101) (00011) (00111) (01001) (00001) (11111) (10001) (11110) (10011) (0010 *) (0100 *) (0111 *) (1110 *) (0010 *) (0000 * ) (00101) (00110) (*****) (*****) (*****)
Now we translate the values into the binary number system (* = 0):
(5) (3) (7) (9) (1) (31) (17) (30) (19) (4) (8) (14) (28) (4) (0) (5) (6) (0) (0) (0 )
Now we calculate the first checksum:
C1 = (5 + 3 + 7 + 9 + 1 + 31 + 17 + 30 + 19 + 4 + 8 + 14 + 28 + 4 + 0 + 5 + 6) mod64 = 191mod64 = 63 = 111111 (now we mirror the checksum) = 111111 (write the resulting number instead of *).
(00101) (00011) (00111) (01001) (00001) (11111) (10001) (11110) (10011) (00101) (01001) (01111) (11101) (00101) (00001) (00101) (00110 ) (*****) (*****) (*****)
Now we calculate the second, third and fourth checksums (we must not forget that due to C1, the values of some positions have changed):
C2 = (31 + 17 + 30 + 19 + 5) mod32 = 102mod32 = 6 = 00110.
C3 = ( 9 + 15 + 29 + 5 + 1) mod32 = 59mod32 = 27 = 11011.
C4 =
00110
XOR
11011
=
11101 = 29 We
write the resulting password in decimal notation:
(5) (3) (7) (9) (1) (31) (17) (30) (19) (5) (9) (15) (29) (5) (1) (5) (6) (6) (27) (29)
Now we encode the resulting values:
5,3,7,9,1 V, H, U, J, 5
9, F, T, 5,1 5,6,6, R, T
- SN = 5th place, PC = 3rd place, RF = 7th place, PD = 9th place, GV = 1st place
- number of points (10341950)
- amount of money (23915840)
- current level (5)
- motorcycle (6)
- all unused bits are zero
We translate the values into a binary number system:
5 = 0101
3 = 0011
7 = 0111
9 = 1001
1 = 0001
10341950 points / 10 = 1034195 = 11111100011111010011
23915840 money / 10 = 2391584 = 1001000111111000100000
level 5 = 101
motorcycle number 6 = 110
We write the raw password and calculate 4 checksums:
(00101) (00011) (00111) (01001) (00001) (11111) (10001) (11110) (10011) (0010 *) (0100 *) (0111 *) (1110 *) (0010 *) (0000 * ) (00101) (00110) (*****) (*****) (*****)
Now we translate the values into the binary number system (* = 0):
(5) (3) (7) (9) (1) (31) (17) (30) (19) (4) (8) (14) (28) (4) (0) (5) (6) (0) (0) (0 )
Now we calculate the first checksum:
C1 = (5 + 3 + 7 + 9 + 1 + 31 + 17 + 30 + 19 + 4 + 8 + 14 + 28 + 4 + 0 + 5 + 6) mod64 = 191mod64 = 63 = 111111 (now we mirror the checksum) = 111111 (write the resulting number instead of *).
(00101) (00011) (00111) (01001) (00001) (11111) (10001) (11110) (10011) (00101) (01001) (01111) (11101) (00101) (00001) (00101) (00110 ) (*****) (*****) (*****)
Now we calculate the second, third and fourth checksums (we must not forget that due to C1, the values of some positions have changed):
C2 = (31 + 17 + 30 + 19 + 5) mod32 = 102mod32 = 6 = 00110.
C3 = ( 9 + 15 + 29 + 5 + 1) mod32 = 59mod32 = 27 = 11011.
C4 =
00110
XOR
11011
=
11101 = 29 We
write the resulting password in decimal notation:
(5) (3) (7) (9) (1) (31) (17) (30) (19) (5) (9) (15) (29) (5) (1) (5) (6) (6) (27) (29)
Now we encode the resulting values:
5,3,7,9,1 V, H, U, J, 5
9, F, T, 5,1 5,6,6, R, T
An example of generating a password with a negative amount of money
Create a password that saves these parameters:
2 = 0010
5 = 0101
8 = 1000
11 = 1011
13 = 1101
5931870 points / 10 = 593187 = 10010000110100100011
83886080 - [- 53724780] = 30161300. 30161300/10 = 3016130 = 1011100000010111000010
level 2 = 010
motorcycle number 3 = 011
(10010) (10101) (11000) (11011) (11101) (10010) (00011) (01001) (00011) (1010 *) (1110 *) (0000 *) (0101 *) (1100 *) (0010 * ) (11010) (11011) (*****) (*****) (*****)
Now we translate the values into the binary number system (* = 0):
(18) (21) (24) (27) (29) (18) (3) (9) (3) (20) (28) (0) (10) (24) (4) (26) (27) (0) (0) (0 )
Now we calculate the first checksum:
C1 = (18 + 21 + 24 + 27 + 29 + 18 + 3 + 9 + 3 + 20 + 28 + 0 + 10 + 24 + 4 + 26 + 7) mod64 = 291mod64 = 35 = 100011 (now we mirror the checksum) = 110001 (write the resulting number instead of *).
(10010) (10101) (11000) (11011) (11101) (10010) (00011) (01001) (00011) (10101) (11101) (00000) (01010) (11000) (00101) (11010) (11011 ) (*****) (*****) (*****)
Now we calculate the second, third and fourth checksums (we must not forget that due to C1, the values of some positions have changed):
C2 = (18 + 3 + 9 + 3 + 21) mod32 = 54mod32 = 22 = 10110
C3 = (29 + 0 + 10 + 24 + 5) mod32 = 68mod32 = 4 = 00100
C4 =
10110
XOR
00100
=
10010 = 18
Write down the resulting password in decimal notation:
(18) (21) (24) (27) (29) (18 ) (3) (9) (3) (21) (29) (0) (10) (24) (5) (26) (27) (22) (4) (18)
Now we encode the resulting values:
I, L, O, R, TI, 3.9.3, L
T, 0, A, O, 5 Q, R, M, 4, I
- SN = 2nd place, PC = 5th place, RF = 8th place, PD = 11th place, GV = 13th place
- number of points (5931870)
- amount of money (-53724780)
- current level (2)
- motorcycle (3)
- all unused bits are equal to one
We translate the values into a binary number system:
2 = 0010
5 = 0101
8 = 1000
11 = 1011
13 = 1101
5931870 points / 10 = 593187 = 10010000110100100011
83886080 - [- 53724780] = 30161300. 30161300/10 = 3016130 = 1011100000010111000010
level 2 = 010
motorcycle number 3 = 011
We write the raw password and calculate 4 checksums:
(10010) (10101) (11000) (11011) (11101) (10010) (00011) (01001) (00011) (1010 *) (1110 *) (0000 *) (0101 *) (1100 *) (0010 * ) (11010) (11011) (*****) (*****) (*****)
Now we translate the values into the binary number system (* = 0):
(18) (21) (24) (27) (29) (18) (3) (9) (3) (20) (28) (0) (10) (24) (4) (26) (27) (0) (0) (0 )
Now we calculate the first checksum:
C1 = (18 + 21 + 24 + 27 + 29 + 18 + 3 + 9 + 3 + 20 + 28 + 0 + 10 + 24 + 4 + 26 + 7) mod64 = 291mod64 = 35 = 100011 (now we mirror the checksum) = 110001 (write the resulting number instead of *).
(10010) (10101) (11000) (11011) (11101) (10010) (00011) (01001) (00011) (10101) (11101) (00000) (01010) (11000) (00101) (11010) (11011 ) (*****) (*****) (*****)
Now we calculate the second, third and fourth checksums (we must not forget that due to C1, the values of some positions have changed):
C2 = (18 + 3 + 9 + 3 + 21) mod32 = 54mod32 = 22 = 10110
C3 = (29 + 0 + 10 + 24 + 5) mod32 = 68mod32 = 4 = 00100
C4 =
10110
XOR
00100
=
10010 = 18
Write down the resulting password in decimal notation:
(18) (21) (24) (27) (29) (18 ) (3) (9) (3) (21) (29) (0) (10) (24) (5) (26) (27) (22) (4) (18)
Now we encode the resulting values:
I, L, O, R, TI, 3.9.3, L
T, 0, A, O, 5 Q, R, M, 4, I

Second Road Rash
Theory
The password consists of 8 positions, each position consists of 5 bits, total 8 * 5 = 40 bits. These bits store these game parameters:
- trails at this level (0-5)
- amount of money (0-327670)
- current level (1-5)
- motorcycle (1-16)
Now let's see what the raw password consists of:
(?, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1) (M, M, M, M, C1) (U, U, L, L, L) (B, B, B, B, C1) (T, T, T, T, T) (C2, C2, C2, C2, C2)
Designations
? - always equal to zero.
U - unused bits.
M is the amount of money (0-327670) in increments = 10. The amount of money is divided by 10 and the resulting number is converted into a binary system.
L is the level number (1-5) in the binary number system.
B - motorcycle number (0-15) in binary system.
| Motorcycles | room |
| SHURIKEN 400 | 0 |
| PANDA 500 | 1 |
| SHURIKEN TT250 | 2 |
| PANDA 900 | 3 |
| BANZAI 7.11 | 4 |
| BANZAI 600 N | 5 |
| BANZAI 750 N | 6 |
| SHURIKEN 1000 N | 7 |
| BANZAI 7.11 N | 8 |
| DIABLO 1000 N | 9 |
| PANDA 600 | 10 |
| BANZAI 600 | eleven |
| BANZAI 750 | 12 |
| SHURIKEN 1000 | thirteen |
| DIABLO 1000 | 14 |
| WILD THING | fifteen |
T - traversed tracks (0-5).
The order of bits from high to low:
4 - is responsible for the passage of the fifth trace.
3 - is responsible for the passage of the fourth route.
2 - is responsible for the passage of the third route.
1 - is responsible for the passage of the second route.
0 - is responsible for the passage of the first track.
C1 = (the sum of positions 1 to 6, not counting the 5th position) mod32 (The resulting number is converted to a binary number system and is mirrored).
C2 = ((sum of positions 1 to 6) mod32) XOR 7 position.
Coding
The encoding of the values is the same as in the first part.
Password Generation Example
Create a password that saves these parameters:
trails completed = 10101
level number 3 = 011
motorcycle number 9 = 1001
193750 money / 10 = 19375 = 100101110101111
(0100 *) (1011 *) (1010 *) (1111 *) (00011) (1001 *) (10101) (*****)
Now we convert the values to the binary number system (* = 0):
(8) ( 22) (20) (30) (3) (18) (21) (0)
Now we calculate the first checksum:
C1 = (8 + 22 + 20 + 30 + 18) mod32 = 98mod32 = 2 = 00010 (now we mirror checksum) = 01000 (write the resulting number instead of *).
(01000) (10111) (10100) (11110) (00011) (10010) (10101) (*****).
Now, we calculate a second checksum (must not forget that for C1, some values have changed positions):
C2 = (8 + 23 + 20 + 30 + 3 + 18) mod32 = 102mod32 = 6mod32 = 00110.
00110
XOR
10101
=
10011 = 19 We
write the resulting password in decimal notation:
(8) (23) (20) (30) (3) (18) (21) (19)
Now we encode the resulting values:
8, N, K, U 3, I, L, J
- passed the fifth, third and first tracks
- amount of money (193,750)
- current level (3)
- motorcycle (9)
- all unused bits are zero
We translate the values into a binary number system:
trails completed = 10101
level number 3 = 011
motorcycle number 9 = 1001
193750 money / 10 = 19375 = 100101110101111
We write the raw password and calculate 2 checksums:
(0100 *) (1011 *) (1010 *) (1111 *) (00011) (1001 *) (10101) (*****)
Now we convert the values to the binary number system (* = 0):
(8) ( 22) (20) (30) (3) (18) (21) (0)
Now we calculate the first checksum:
C1 = (8 + 22 + 20 + 30 + 18) mod32 = 98mod32 = 2 = 00010 (now we mirror checksum) = 01000 (write the resulting number instead of *).
(01000) (10111) (10100) (11110) (00011) (10010) (10101) (*****).
Now, we calculate a second checksum (must not forget that for C1, some values have changed positions):
C2 = (8 + 23 + 20 + 30 + 3 + 18) mod32 = 102mod32 = 6mod32 = 00110.
00110
XOR
10101
=
10011 = 19 We
write the resulting password in decimal notation:
(8) (23) (20) (30) (3) (18) (21) (19)
Now we encode the resulting values:
8, N, K, U 3, I, L, J
But that is not all!
I have prepared something else ...
For dessert - Banana Prince
Let's digress a bit from the Sega console and move on to Nes (Dandy). This game very badly ruined my nerves. Who played, he remembers the long questions in Japanese, because of which the passage of the game turns into hell. The passwords in it are simple, but with a subtle emphasis. To complete the game 100% it was necessary to collect 4 armor. But there is one problem, in order to get them, it was necessary to answer a ton of questions. No matter how I delved into the Internet and in my code book, I never found the passwords that save the collected armor. And without them, the final boss will send you far away a ton of Japanese characters. But delving into the assignments of the bits, I found that the game saves:
- current level number (0-20) in decimal system
- weapon number (0-15)
- armor (0-4)
The password consists of 8 positions, each position consists of 2 bits, total 8 * 2 = 16 bits.
Now let's see what the raw password consists of:
(C, C) (A, L) (L, L) (L, L) (C, C) (G, G) (A, A) (G, G)
Designations
C = (the sum of all positions except 1 and 5) in the binary system. The two most significant bits of the checksum are written to the 5th position, and the two least significant bits to the 1 position.
A is the number of armor (0-4) in the binary number system.
L is the level number (0-20) in the binary number system.
| Levels | room |
| 1-1 | 0 |
| 1-2 | 1 |
| 1-3 | 2 |
| 2-1 | 3 |
| 2-2 | 4 |
| 2-3 | 5 |
| 3-1 | 6 |
| 3-2 | 7 |
| 3-3 | 8 |
| 4-1 | 9 |
| 4-2 | 10 |
| 4-3 | eleven |
| 5-1 | 12 |
| 5-2 | thirteen |
| 5-3 | 14 |
| 6-1 | fifteen |
| 6-2 | 16 |
| 6-3 | 17 |
| 7-1 | 18 |
| 7-2 | 19 |
| 7-3 | 20 |
G - weapon number (0-15) in the binary system.
Coding
For coding, 4 degrees of eating a banana are used, which we denote by numbers:
 = 0
= 0 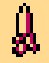 = 1
= 1  = 2
= 2  = 3
= 3Пример генерации пароля
Создадим пароль, который сохраняет данные параметры:
4 = 100
20 = 10100
15 = 1111
(**) (11) (01) (00) (**) (11) (00) (11)
Теперь переводим значения в двоичную систему счисления (* =0):
(0) (3) (1) (0) (0) (3) (0) (3)
Вычисляем контрольную сумму:
C= (3+1+0+3+0+3)= 10= 1010. 10(два старших бита)10(два младших бита).
Записываем получившийся пароль в десятичной системе счисления:
(2) (3) (1) (0) (2) (3) (0) (3)
Осталось перевести цифры в банановый эквивалент.
- персонаж имеет 4 доспеха
- номер уровня (20)
- номер оружия (15)
Переводим значения в двоичную систему счисления:
4 = 100
20 = 10100
15 = 1111
Записываем сырой пароль:
(**) (11) (01) (00) (**) (11) (00) (11)
Теперь переводим значения в двоичную систему счисления (* =0):
(0) (3) (1) (0) (0) (3) (0) (3)
Вычисляем контрольную сумму:
C= (3+1+0+3+0+3)= 10= 1010. 10(два старших бита)10(два младших бита).
Записываем получившийся пароль в десятичной системе счисления:
(2) (3) (1) (0) (2) (3) (0) (3)
Осталось перевести цифры в банановый эквивалент.
Заключение
So we went to the finish line.

What would I like to say? Well, I hope this article is useful to someone. Good luck, thanks for reading.
