Growth of hockey players: we analyze the data of all world championships in the current century
The other day ended the next world hockey championship.
Watching the matches, an idea was born. When during the breaks the television camera shows the players leaving for the locker room, it’s hard not to notice how huge they are. Against the background of coaches, team functionaries, employees of the ice arena, journalists or just fans, they usually look very impressive.
And I wondered. Are hockey players above ordinary people? How does the growth of hockey players change over time compared to ordinary people? Are there persistent cross-country differences?
Data
IIHF, the organization hosting the world hockey championships, annually publishes the lineups of participating teams with information on the height and weight of each player. An archive of this data is here .
I gathered together the data of all the world championships from 2001 to 2016. From year to year, the format for providing data is slightly changing, which requires some effort to clean it. Not imagining how to correctly automate the process, I copied all the data manually, which took a little more than 3 hours. The combined dataset has been posted publicly .
# load required packages
require(dplyr) # data manipulation
require(lubridate) # easy manipulations with dates
require(ggplot2) # visualization
require(ggthemes) # themes for ggplot2
require(cowplot) # nice alignment of the ggplots
require(RColorBrewer) # generate color palettes
require(texreg) # easy export of regression tables
require(xtable) # export a data frame into an html table# download the IIHF data set; if there are some problems, you can download manually# using the stable URL (https://dx.doi.org/10.6084/m9.figshare.3394735.v2)
df <- read.csv('https://ndownloader.figshare.com/files/5303173')
# color palette
brbg11 <- brewer.pal(11,'BrBG')Are hockey players growing up? Rough (periodic) comparison
To begin with, we compare the average growth of players in all 16 world championships.

# mean height by championship
df_per <- df %>% group_by(year) %>%
summarise(height=mean(height))
gg_period_mean <- ggplot(df_per, aes(x=year,y=height))+
geom_point(size=3,color=brbg11[9])+
stat_smooth(method='lm',size=1,color=brbg11[11])+
ylab('height, cm')+
xlab('year of competition')+
scale_x_continuous(breaks=seq(2005,2015,5),labels=seq(2005,2015,5))+
theme_few(base_size = 15)+
theme(panel.grid=element_line(colour = 'grey75',size=.25))
gg_period_jitter <- ggplot(df, aes(x=year,y=height))+
geom_jitter(size=2,color=brbg11[9],alpha=.25,width = .75)+
stat_smooth(method='lm',size=1,se=F,color=brbg11[11])+
ylab('height, cm')+
xlab('year of competition')+
scale_x_continuous(breaks=seq(2005,2015,5),labels=seq(2005,2015,5))+
theme_few(base_size = 15)+
theme(panel.grid=element_line(colour = 'grey75',size=.25))
gg_period <- plot_grid(gg_period_mean,gg_period_jitter)The positive trend is obvious. Over a decade and a half, the average growth of a hockey player at the World Cup increased by almost 2 centimeters (left panel). As if a slight increase against the backdrop of a fairly large variation (right panel). Is it a lot or a little? To answer the question, it is necessary to correctly compare with the population (but more on this at the end of the article).
Cohort analysis
A more correct way to study changes in growth involves a comparison of birth cohorts. Here we are faced with a curious nuance - some hockey players participated in more than one world championship. Question: Do I clean out duplicate recordings for the same people? If we are interested in the average growth of a hockey player in the championship (as in the picture above), it probably does not make sense to clear out. But if we want to track the change in growth of hockey players as such, in my opinion, it would be wrong to assign more weight to those players who regularly got to the world championships. Therefore, for further analysis, I cleared the data from repeated entries of the same players.
# remove double counts
dfu_h <- df %>% select(year,name,country,position,birth,cohort,height) %>%
spread(year,height)
dfu_h$av.height <- apply(dfu_h[,6:21],1,mean,na.rm=T)
dfu_h$times_participated <- apply(!is.na(dfu_h[,6:21]),1,sum)
dfu_w <- df %>% select(year,name,country,position,birth,cohort,weight) %>%
spread(year,weight)
dfu_w$av.weight <- apply(dfu_w[,6:21],1,mean,na.rm=T)
dfu <- left_join(dfu_h %>% select(name,country,position,birth,cohort,av.height,times_participated),
dfu_w %>% select(name,country,position,birth,cohort,av.weight),
by = c('name','country','position','birth','cohort')) %>%
mutate(bmi = av.weight/(av.height/100)^2)The total number of observations decreased from 6292 to 3333. If the hockey player participated in more than one World Championship, I averaged the height and weight data, since the height and (in particular) the weight of an individual hockey player could change over time. How many times do hockey players earn the honor of playing for national teams at world championships? On average a little less than 2 times.
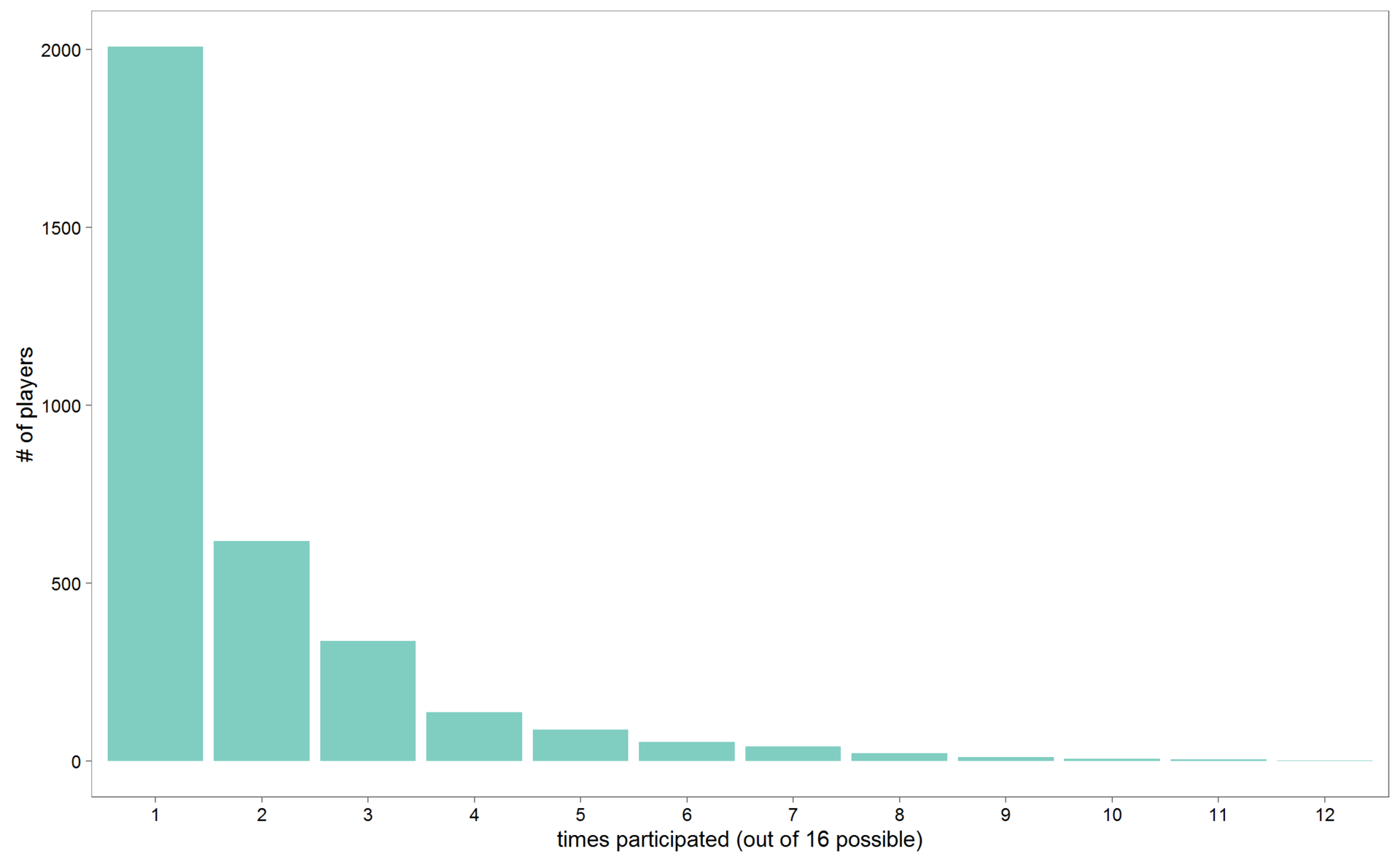
# frequencies of participation in world championships
mean(dfu$times_participated)
df_part <- as.data.frame(table(dfu$times_participated))
gg_times_part <- ggplot(df_part,aes(y=Freq,x=Var1))+
geom_bar(stat='identity',fill=brbg11[9])+
ylab('# of players')+
xlab('times participated (out of 16 possible)')+
theme_few(base_size = 15)But there are unique ones. Let's see which of the players participated in at least 10 world championships. There were 14 such players.
# the leaders of participation in world championships# save the table to html
leaders <- dfu %>% filter(times_participated > 9)
View(leaders)
print(xtable(leaders), type="html", file="table_leaders.html")| name | country | position | birth | cohort | av.height | times_participated | av.weight | bmi | |
|---|---|---|---|---|---|---|---|---|---|
| one | ovechkin alexander | RUS | F | 1985-09-17 | 1985 | 188.45 | eleven | 98.36 | 27.70 |
| 2 | nielsen daniel | Den | D | 1980-10-31 | 1980 | 182.27 | eleven | 79.73 | 24.00 |
| 3 | staal kim | Den | F | 1978-03-10 | 1978 | 182.00 | ten | 87.80 | 26.51 |
| four | green morten | Den | F | 1981-03-19 | 1981 | 183.00 | 12 | 85.83 | 25.63 |
| five | masalskis edgars | Lat | G | 1980-03-31 | 1980 | 176.00 | 12 | 79.17 | 25.56 |
| 6 | ambuhl andres | SUI | F | 1983-09-14 | 1983 | 176.80 | ten | 83.70 | 26.78 |
| 7 | granak dominik | SVK | D | 1983-06-11 | 1983 | 182.00 | ten | 79.50 | 24.00 |
| eight | madsen morten | Den | F | 1987-01-16 | 1987 | 189.82 | eleven | 86.00 | 23.87 |
| 9 | redlihs mikelis | Lat | F | 1984-07-01 | 1984 | 180.00 | ten | 80.40 | 24.81 |
| ten | cipulis martins | Lat | F | 1980-11-29 | 1980 | 180.70 | ten | 82.10 | 25.14 |
| eleven | holos jonas | Nor | D | 1987-08-27 | 1987 | 180.18 | eleven | 91.36 | 28.14 |
| 12 | bastiansen anders | Nor | F | 1980-10-31 | 1980 | 190.00 | eleven | 93.64 | 25.94 |
| 13 | ask morten | Nor | F | 1980-05-14 | 1980 | 185.00 | ten | 88.30 | 25.80 |
| 14 | forsberg kristian | Nor | F | 1986-05-05 | 1986 | 184.50 | ten | 87.50 | 25.70 |
Alexander Ovechkin, 11 times! But here it should be noted that, in principle, it was not possible for all hockey players to participate in all 16 championships: the birth cohort (how much the playing career intersected with this particular observation period) depends on whether the player’s team participated in all world championships (see figure 3) and whether the player got into the national team stably; finally there is the NHL stably distracting the best of the best from participating in world championships.

# countries times participated
df_cnt_part <- df %>% select(year,country,no) %>%
mutate(country=factor(paste(country))) %>%
group_by(country,year) %>%
summarise(value=sum(as.numeric(no))) %>%
mutate(value=1) %>%
ungroup() %>%
mutate(country=factor(country, levels = rev(levels(country))),
year=factor(year))
d_cnt_n <- df_cnt_part %>% group_by(country) %>%
summarise(n=sum(value))
gg_cnt_part <- ggplot(data = df_cnt_part, aes(x=year,y=country))+
geom_point(color=brbg11[11],size=7)+
geom_text(data=d_cnt_n,aes(y=country,x=17.5,label=n,color=n),size=7,fontface=2)+
geom_text(data=d_cnt_n,aes(y=country,x=18.5,label=' '),size=7)+
scale_color_gradientn(colours = brbg11[7:11])+
xlab(NULL)+
ylab(NULL)+
theme_bw(base_size = 25)+
theme(legend.position='none',
axis.text.x = element_text(angle = 90, hjust = 1,vjust=0.5))Are hockey players growing up? Regression analysis
Regression analysis allows you to more correctly answer the question about changing players' growth. In this case, using a multinomial linear regression, the growth of a hockey player is predicted depending on the birth cohort. Including various additional (control) variables in the specification of the regression model, we obtain the value of the coefficient “ceteris paribus” that is most interesting to us. For example, adding to the explanatory variables, in addition to the birth cohort, the player’s position on the field, we get the relationship of growth and cohort, cleared of the effect of differences depending on position; adding to the control variables of the country, we get the result, cleared of cross-country differences. Of course, if the control variables themselves are significant, this is also worth paying attention to.
Regression models (especially linear regressions) are very sensitive to outliers (see, for example, this article ). Without going deep into this broad topic, I just removed from the analysis the cohorts for which we have too few representatives.
# remove small cohorts
table(dfu$cohort)
dfuc <- dfu %>% filter(cohort<1997,cohort>1963)Not wanting to cut the data much, I removed only the cohorts of 1963, 1997 and 1998, for which we have less than 10 players.
So, the results of regression analysis. In each next model, I add one variable.
Dependent variable : hockey player growth.
Explanatory variables : 1) birth cohort; 2) + position on the field (comparison with defenders); 3) + country (comparison with Russia).
# relevel counrty variable to compare with Russia
dfuc$country <- relevel(dfuc$country,ref = 'RUS')
# regression models
m1 <- lm(data = dfuc,av.height~cohort)
m2 <- lm(data = dfuc,av.height~cohort+position)
m3 <- lm(data = dfuc,av.height~cohort+position+country)
# export the models to html
htmlreg(list(m1,m2,m3),file = 'models_height.html',single.row = T)| Model 1 | Model 2 | Model 3 | ||
|---|---|---|---|---|
| (Intercept) | -10.17 (27.67) | -18.64 (27.01) | 32.59 (27.00) | |
| cohort | 0.10 (0.01) *** | 0.10 (0.01) *** | 0.08 (0.01) *** | |
| positionF | -2.59 (0.20) *** | -2.59 (0.20) *** | ||
| positionG | -1.96 (0.31) *** | -1.93 (0.30) *** | ||
| countryAUT | -0.94 (0.55) | |||
| countryBLR | -0.95 (0.53) | |||
| countryCAN | 1.13 (0.46) * | |||
| countryCZE | 0.56 (0.49) | |||
| countryDEN | -0.10 (0.56) | |||
| countryFIN | 0.20 (0.50) | |||
| countryFRA | -2.19 (0.69) ** | |||
| countryGER | -0.61 (0.51) | |||
| countryHUN | -0.61 (0.86) | |||
| countryITA | -3.58 (0.61) *** | |||
| countryJPN | -5.24 (0.71) *** | |||
| countryKAZ | -1.16 (0.57) * | |||
| countryLAT | -1.38 (0.55) * | |||
| countryNOR | -1.61 (0.62) ** | |||
| countryPOL | 0.06 (1.12) | |||
| countrySLO | -1.55 (0.58) ** | |||
| countrySUI | -1.80 (0.53) *** | |||
| countrySVK | 1.44 (0.50) ** | |||
| countrySWE | 1.18 (0.48) * | |||
| countryUKR | -1.82 (0.59) ** | |||
| countryUSA | 0.54 (0.45) | |||
| R 2 | 0.01 | 0.06 | 0.13 | |
| Adj. R 2 | 0.01 | 0.06 | 0.12 | |
| Num. obs. | 3319 | 3319 | 3319 | |
| Rmse | 5.40 | 5.27 | 5.10 | |
| *** p <0.001, ** p <0.01, * p <0.05 | ||||
Model Interpretation
Model 1 . A one-year increase in the cohort corresponds to an increase in the growth of hockey players by 0.1 cm. The coefficient is statistically significant, but the model explains only 1% of the variation of the dependent variable. In principle, this is not a problem, since the simulation is explanatory in nature, the task of prediction is not posed. However, a low coefficient of determination indicates that there should be other variables that better explain the differences between hockey players in height.
Model 2 . Defenders are the highest players in hockey. Goalkeepers are 2 cm lower and attackers are 2.6 cm lower. All odds are statistically significant. The explained variation of the dependent variable increases to 6%. In this case, the coefficient of a variable birth cohort does not change.
Model 3 . Adding control variables for countries is curious for two reasons. First, some differences are statistically significant and interesting in themselves. For example, Swedes, Slovaks and Canadians are statistically significantly higher than our players. Most of the nations are much lower than us, the Japanese are as much as 5.2 cm, Italians by 3.6 cm, the French by 2.2 cm (see also Figure 4). Secondly, the introduction of control variables for countries significantly reduces the coefficient for the variable cohort of birth - to 0.08. This means that cross-country differences explain part of the differences in birth cohorts. The coefficient of determination of the model increases to 13%.

# players' height by country
gg_av.h_country <- ggplot(dfuc ,aes(x=factor(cohort),y=av.height))+
geom_point(color='grey50',alpha=.25)+
stat_summary(aes(group=country),geom='line',fun.y = mean,size=.5,color='grey50')+
stat_smooth(aes(group=country,color=country),geom='line',size=1)+
#geom_hline(yintercept = mean(height),color='red',size=.5)+
facet_wrap(~country,ncol=4)+
coord_cartesian(ylim = c(170,195))+
scale_x_discrete(labels=paste(seq(1965,1995,10)),breaks=paste(seq(1965,1995,10)))+
theme_few(base_size = 15)+
theme(legend.position='none',
panel.grid=element_line(colour = 'grey75',size=.25))The most complete model shows that an increase in hockey players' growth occurs at a rate of 0.08 cm per year. This means an increase of 0.8 cm per decade or 2.56 cm in 32 years from 1964 to 1996. Note that when controlling variables are taken into account, the growth rate of hockey players is about one and a half times lower than with a more rough analysis of average values (Figure 1): 0.8 cm per decade versus about 1.2 cm.
Before we finally try to understand how significant the increase in growth is, I want to pay attention to one more curious point. The introduction of control variables implies fixing the differences between the categories with a single slope of the regression line (a single coefficient for the main explanatory variable). This is not always good and can mask significant differences in the tightness of the relationship between the studied variables in the subsamples. For example, a separate simulation of the dependence of player growth on the role (Figure 5) shows that the relationship is most pronounced for goalkeepers and least noticeable for defenders.

dfuc_pos <- dfuc
levels(dfuc_pos$position) <- c('Defenders','Forwards','Goalkeeprs')
gg_pos <- ggplot(dfuc_pos ,aes(x=cohort,y=av.height))+
geom_jitter(aes(color=position),alpha=.5)+
stat_smooth(method = 'lm', se = T,color=brbg11[11],size=1)+
scale_x_continuous(labels=seq(1965,1995,5),breaks=seq(1965,1995,5))+
scale_color_manual(values = brbg11[c(8,4,10)])+
facet_wrap(~position,ncol=3)+
xlab('birth cohort')+
ylab('height, cm')+
theme_few(base_size = 20)+
theme(legend.position='none',
panel.grid=element_line(colour = 'grey75',size=.25))# separate models for positions
m3d <- lm(data = dfuc %>% filter(position=='D'),av.height~cohort+country)
m3f <- lm(data = dfuc %>% filter(position=='F'),av.height~cohort+country)
m3g <- lm(data = dfuc %>% filter(position=='G'),av.height~cohort+country)
htmlreg(list(m3d,m3f,m3g),file = '2016/160500 Hockey players/models_height_pos.html',single.row = T,
custom.model.names = c('Model 3 D','Model 3 F','Model 3 G'))| Model 3 D | Model 3 F | Model 3 G | ||
|---|---|---|---|---|
| (Intercept) | 108.45 (46.46) * | 49.32 (36.73) | -295.76 (74.61) *** | |
| cohort | 0.04 (0.02) | 0.07 (0.02) *** | 0.24 (0.04) *** | |
| countryAUT | 0.14 (0.96) | -2.01 (0.75) ** | 0.47 (1.47) | |
| countryBLR | 0.30 (0.87) | -1.53 (0.73) * | -2.73 (1.55) | |
| countryCAN | 1.55 (0.78) * | 0.39 (0.62) | 3.45 (1.26) ** | |
| countryCZE | 0.87 (0.84) | 0.30 (0.67) | 0.63 (1.36) | |
| countryDEN | -0.60 (0.95) | 0.10 (0.75) | -0.19 (1.62) | |
| countryFIN | -0.55 (0.89) | -0.04 (0.67) | 2.40 (1.32) | |
| countryFRA | -3.34 (1.15) ** | -2.06 (0.93) * | 1.39 (2.07) | |
| countryGER | 0.48 (0.85) | -1.40 (0.72) | -0.65 (1.33) | |
| countryHUN | -1.32 (1.47) | -0.70 (1.16) | 0.65 (2.39) | |
| countryITA | -2.08 (1.08) | -4.78 (0.82) *** | -2.02 (1.62) | |
| countryJPN | -4.13 (1.26) ** | -6.52 (0.94) *** | -2.27 (1.98) | |
| countryKAZ | -1.23 (0.95) | -1.82 (0.79) * | 1.79 (1.58) | |
| countryLAT | -0.73 (0.95) | -1.39 (0.75) | -3.42 (1.49) * | |
| countryNOR | -3.25 (1.07) ** | -1.06 (0.85) | -0.10 (1.66) | |
| countryPOL | 0.82 (1.89) | -0.58 (1.55) | 0.37 (2.97) | |
| countrySLO | -1.57 (0.99) | -1.54 (0.79) | -2.25 (1.66) | |
| countrySUI | -1.98 (0.91) * | -2.36 (0.71) *** | 1.12 (1.47) | |
| countrySVK | 2.94 (0.87) *** | 0.81 (0.67) | -0.70 (1.50) | |
| countrySWE | 0.75 (0.81) | 1.24 (0.65) | 1.37 (1.33) | |
| countryUKR | -1.37 (1.01) | -1.77 (0.80) * | -3.71 (1.66) * | |
| countryUSA | 0.76 (0.78) | -0.08 (0.62) | 2.58 (1.26) * | |
| R 2 | 0.09 | 0.10 | 0.24 | |
| Adj. R 2 | 0.07 | 0.09 | 0.20 | |
| Num. obs. | 1094 | 1824 | 401 | |
| Rmse | 5.08 | 5.08 | 4.87 | |
| *** p <0.001, ** p <0.01, * p <0.05 | ||||
Separate modeling shows that in the cohorts of 1964-1996 years of birth, the average growth of hockey players participating in the world championships in 2001-2016 increased at a speed of 0.4 cm per decimal for defenders, 0.7 cm for attackers and (!) 2.4 cm for goalkeepers. Over three decades, the average growth of goalkeepers increased by 7 cm!
The time has come to compare these changes with population averages.
Comparison with the population
The results of the regression analysis record significant cross-country differences. Therefore, it makes sense to compare by country: hockey players of a certain country with the male population of the same country.
To compare the growth of hockey players with the average male population, I used data from a relevant scientific article ( PDF ). I copied the data from the article (using the wonderful tabula program ) and also posted it in the public domain .
# download the data from Hatton, T. J., & Bray, B. E. (2010). # Long run trends in the heights of European men, 19th–20th centuries. # Economics & Human Biology, 8(3), 405–413. # http://doi.org/10.1016/j.ehb.2010.03.001# stable URL, copied data (https://dx.doi.org/10.6084/m9.figshare.3394795.v1)
df_hb <- read.csv('https://ndownloader.figshare.com/files/5303878')
df_hb <- df_hb %>%
gather('country','h_pop',2:16) %>%
mutate(period=paste(period)) %>%
separate(period,c('t1','t2'),sep = '/')%>%
transmute(cohort=(as.numeric(t1)+as.numeric(t2))/2,country,h_pop)
# calculate hockey players' cohort height averages for each country
df_hoc <- dfu %>% group_by(country,cohort) %>%
summarise(h_hp=mean(av.height)) %>%
ungroup()Unfortunately, data on population growth dynamics intersect only with 8 countries from my hockey dataset: Austria, Denmark, Finland, France, Germany, Italy, Norway, Sweden.
# countries in both data sets
both_cnt <- levels(factor(df_hb$country))[which(levels(factor(df_hb$country)) %in% levels(df_hoc$country))]
both_cnt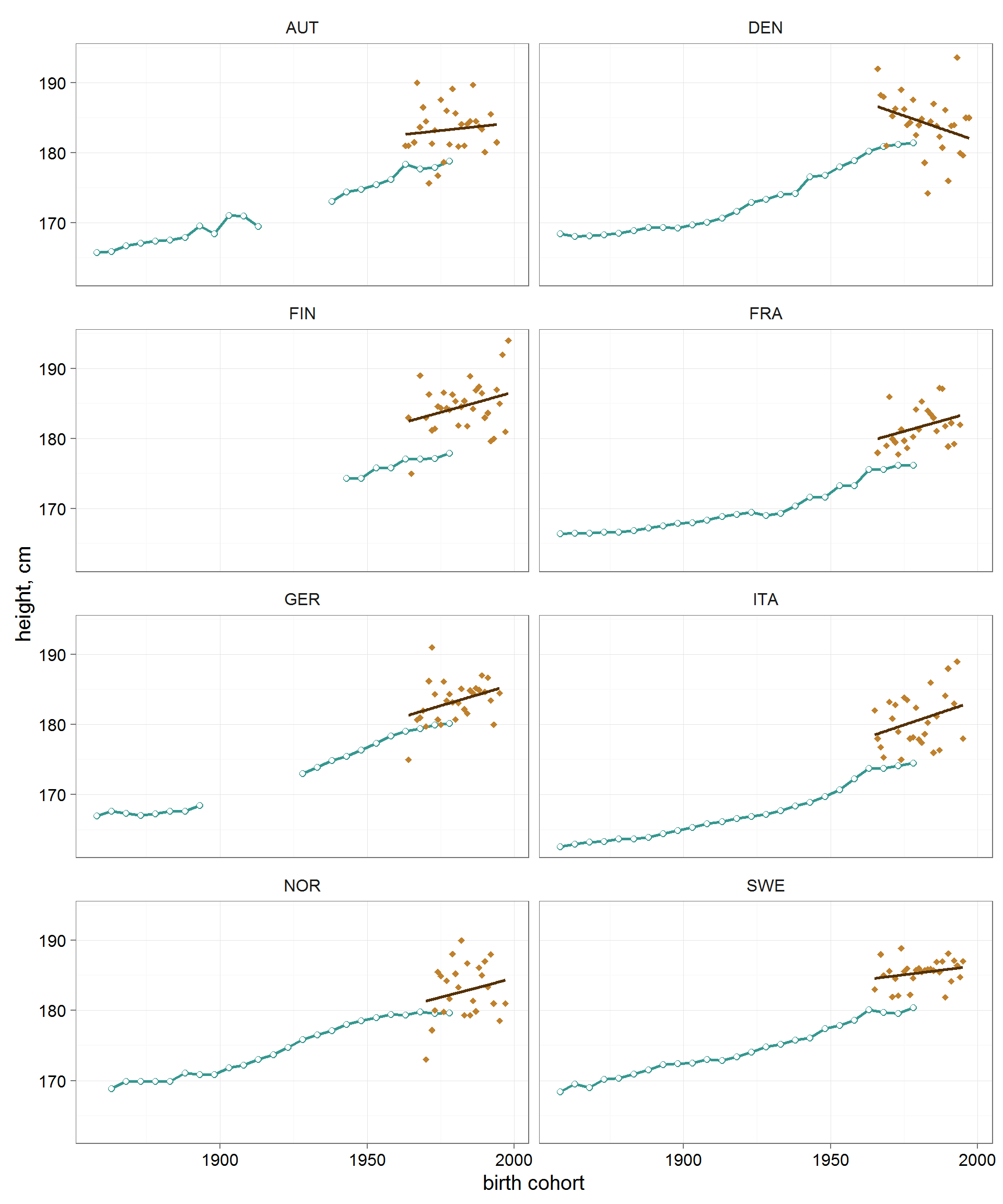
gg_hoc_vs_pop <- ggplot()+
geom_path(data = df_hb %>% filter(country %in% both_cnt), aes(x=cohort,y=h_pop),
color=brbg11[9],size=1)+
geom_point(data = df_hb %>% filter(country %in% both_cnt), aes(x=cohort,y=h_pop),
color=brbg11[9],size=2)+
geom_point(data = df_hb %>% filter(country %in% both_cnt), aes(x=cohort,y=h_pop),
color='white',size=1.5)+
geom_point(data = df_hoc %>% filter(country %in% both_cnt), aes(x=cohort,y=h_hp),
color=brbg11[3],size=2,pch=18)+
stat_smooth(data = df_hoc %>% filter(country %in% both_cnt), aes(x=cohort,y=h_hp),
method='lm',se=F,color=brbg11[1],size=1)+
facet_wrap(~country,ncol=2)+
ylab('height, cm')+
xlab('birth cohort')+
theme_few(base_size = 15)+
theme(panel.grid=element_line(colour = 'grey75',size=.25))In all the countries analyzed, hockey players are 2-5 cm higher than standard statistical men. But this is not surprising - there is significant selection in sports.
Another thing is noteworthy. In developed countries, a particularly rapid increase in male population growth occurred in the first mid-20th century. In cohorts around the 1960s, male growth approached a plateau and ceased to increase rapidly. The average growth trend of hockey players in all countries (except for some reason Denmark) seemed to continue the long-standing trend of the entire male population.
For cohorts of Europeans born in the first half of the 20th century, the growth rate of average growth ranged from 1.18 to 1.74 cm per decade, depending on the country (Figure 7). Since the 1960s, this indicator has dropped to the level of 0.15-0.80 over 10 years.

# growth in population
df_hb_w <- df_hb %>% spread(cohort,h_pop)
names(df_hb_w)[2:26] <- paste('y',names(df_hb_w)[2:26])
diffs <- df_hb_w[,3:26]-df_hb_w[,2:25]
df_hb_gr<- df_hb_w %>%
transmute(country,
gr_1961_1980 = unname(apply(diffs[,22:24],1,mean,na.rm=T))*2,
gr_1901_1960 = unname(apply(diffs[,9:21],1,mean,na.rm=T))*2,
gr_1856_1900 = unname(apply(diffs[,1:8],1,mean,na.rm=T))*2) %>%
gather('period','average_growth',2:4) %>%
filter(country %in% both_cnt) %>%
mutate(country=factor(country,levels = rev(levels(factor(country)))),
period=factor(period,labels = c('1856-1900','1901-1960','1961-1980')))
gg_hb_growth <- ggplot(df_hb_gr, aes(x=average_growth,y=country))+
geom_point(aes(color=period),size=3)+
scale_color_manual(values = brbg11[c(8,3,10)])+
scale_x_continuous(limits=c(0,2))+
facet_wrap(~period)+
theme_few()+
xlab("average growth in men's height over 10 years, cm")+
ylab(NULL)+
theme_few(base_size = 20)+
theme(legend.position='none',
panel.grid=element_line(colour = 'grey75',size=.25))Against the backdrop of a stagnant trend in the population, an increase in the growth of hockey players looks very impressive. And the acceleration among goalkeepers is generally unprecedented.
Do not forget about selection. The divergence of trends in the population and among hockey players probably indicates an increasing selection - hockey requires ever greater growth for a successful career.
Sport selection
Looking through the scientific literature on the topic, I came across a remarkable result . It turns out that in professional sports people born in the first half of the year predominate. This is explained by the fact that sports sections, as a rule, form children's teams for birth cohorts. Thus, those born at the beginning of the year always have a little more time spent behind them, which is often directly expressed in physical superiority over peers born at the end of the year. It is easy to verify this result on our dataset.

# check if there are more players born in earlier months
df_month <- df %>% mutate(month=month(birth)) %>%
mutate(month=factor(month,levels = rev(levels(factor(month)))))
gg_month <- ggplot(df_month,aes(x=factor(month)))+
geom_bar(stat='count',fill=brbg11[8])+
scale_x_discrete(breaks=1:12,labels=month.name)+
xlab('month of birth')+
coord_flip()+
theme_few(base_size = 20)+
theme(legend.position='none',
panel.grid=element_line(colour = 'grey75',size=.25))Indeed, the distribution is rather strongly biased towards the early months. If we disaggregate the data by decades of birth, then with the naked eye it can be seen that the effect intensifies with time (Figure 9). Indirectly, this indicates that selection in hockey is becoming tougher.

# facet by decades
df_month_dec <- df_month %>%
mutate(dec=factor(substr(paste(cohort),3,3),labels = paste('born in',c('1960s','1970s','1980s','1990s'))))
gg_month_dec <- ggplot(df_month_dec,aes(x=factor(month)))+
geom_bar(stat='count',fill=brbg11[8])+
scale_x_discrete(breaks=1:12,labels=month.abb)+
xlab('month of birth')+
facet_wrap(~dec,ncol=2,scales = 'free')+
theme_few(base_size = 20)+
theme(legend.position='none',
panel.grid=element_line(colour = 'grey75',size=.25))For the future
It will be interesting to see if physical data affects the game statistics of hockey players. I came across an entertaining article published in a very decent scientific journal in which the authors found a correlation between the ratio of the proportions of a hockey player's face and the average number of penalty minutes per game.
Reproducibility
The full R script reproducing the results of my article is here .
Used version R-3.2.4
All packages as of 2016-03-14. In the case of package incompatibilities, this code will be guaranteed to be reproduced when using the checkpoint package with the corresponding date.



