How PageRank works: implementation in the R language through linear algebra and power-method
- Tutorial
Hi, habrovchane!
My name is Aleksey. This time I broadcast from a workplace in ITAR-TASS.
In this short text, I'll introduce you to a method for calculating PageRank © (hereinafter will call it PR) on simple, clear examples, in the language of R. The algorithm is an intellectual property of Google, but, in view of its usefulness for data analysis tasks, apply a lot of public tasks , which can be reduced to the search for large nodes on the graph and ranking them by significance.
Mention of a large company in a post is not an advertisement.
Since I am not a professional mathematician, I use this article and this tutorial as a guide, and I recommend you .
Understanding how this works is not difficult. There is a set of elements that are interconnected. This is how they are related - this is a broad question: maybe through links (like Google’s), perhaps through references to each other (almost the same links), the probabilities of transitions between elements (the Markov process matrix) can be given a priori sense of communication. I would like to assign to these elements a certain criterion of importance, which would carry information about the probability that a given element will be visited by some abstract particle traveling along the graph in the diffusion process.
Um, that doesn't sound very clear. It's easier to imagine a guy forpoppya laptop that surfs the pages from the search results, smoking a hookah, follows links from one page to another and more and more often end up on the same page (or pages).
This is due to the fact that some of the pages that he visits contain such interesting information in the original source, that other pages have to reprint it with an indication of the link.
This guy on Google was called Random surfer. It is a particle in the process of diffusion: a discrete change of position on a graph over time. And the probability with which he will visit the page with diffusion time tending to infinity is the PR.
We agree - we work with 10 elements, in such a small, cozy graphchik.
Each of the 10 elements (nodes) contains from 10 to 14 references to other nodes in random order, excluding itself. At the moment, we just decide that these references are web links.
It is clear that it may happen that some of the elements are mentioned more often than others. Check it out.
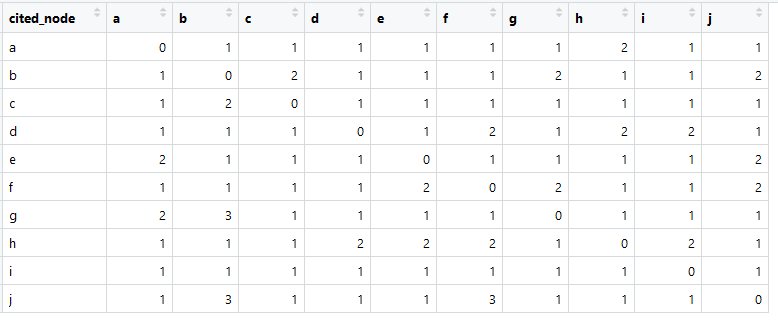
This is our link matrix (usually called adjacency matrix in English).
The amount in each column is greater than zero, which means there is a connection from each element to any other element (this is important for further analysis).
We can create on the basis of this table the so-called Affinity matrix, or, in our opinion, the proximity matrix (and also call it the transition matrix), which mathematicians call the stochastic matrix (column-stochastic matrix): main source
Let's assign it to a variable with the name A.
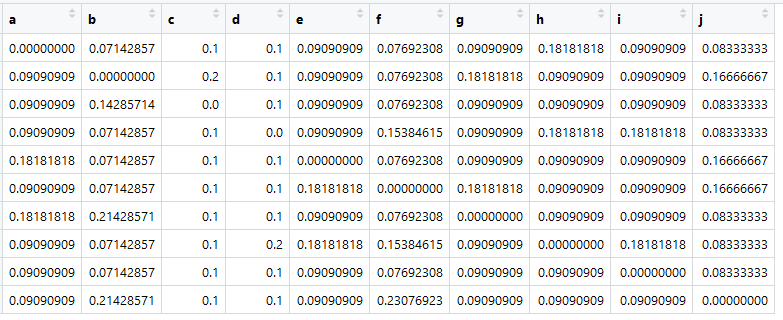
Most the main thing now is that the sum in all columns is one.
Here it is - the transition matrix, it is Markov, it is similar. Tsifir is the probability of transitions from an element in a column to an element in a line.
This, of course, is not real "similarity." These would be, for example, if you count the cosine of the angle between the presentation of documents. But it is important that the transition matrix is reduced to (pseudo-) probabilities, so that the sum for each column is equal to one.
Let's look at the Markov transition graph (our A):
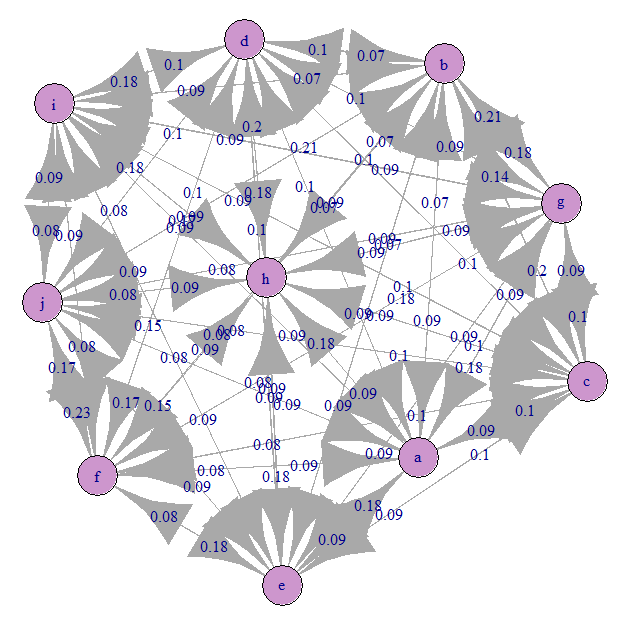
Everything is approximately evenly confused). This is because we have given equiprobable transitions.
And now is the time of magic!
For a stochastic matrix A, the first eigenvalue must be equal to one, and the corresponding eigenvector is the PageRank vector.
This is the vector of PR values - this is the normalized eigenvector of the transition matrix A, corresponding to the eigenvalue of this matrix, equal to one, the dominant eigenvector.
Now you can rank the elements. But due to the nature of the experiment, they have a very similar weight.
The transition matrix A may not satisfy the conditions of stochasticity.
Firstly, there may be elements that do not refer to anywhere, that is, with the lack of feedback (they themselves can be referenced). For large real-life graphs, this is a very likely problem. This means that one of the columns of the matrix will have only zeros. In this case, the solution through eigenvectors will not work.
Google solved this problem by filling the column with a uniform probability distribution p = 1 / N. Where N is the number of all elements.
Secondly, in the graph there may be elements with feedback on each other, but not other elements of the graph. This is also an insurmountable problem for linear algebra due to the violation of assumptions.
It is solved by introducing a constant called the Damping factor, which denotes the a priori probability of transition from any element to any other, even if there are no physical references. In other words, diffusion is possible when it hits any state.
If we apply these transformations to our matrix, then it can again be solved through eigenvectors!
Thirdly, the matrix can be trivial, not square, and this is critical! I will not dwell on this moment, because I believe that you yourself will figure out how to fix it.
But there is a faster and more accurate method, which is also more economical in memory (which may be relevant for large graphs): Power method.
Voila!
On this I will finish the tutorial. Hope you find it useful.
I forgot to say that to build a transition matrix (probabilities) you can use the similarity of texts, the number of mentions, the fact that there is a link, and other metrics that are reduced to pseudo-probabilities or are probabilities. A rather interesting example is the ranking of sentences in the text on the matrix of similarity of the bags of the words tf-idf to highlight the sentence of the sum of all the text. There may be other creative uses of PR.
I recommend trying to play independently with the transition matrix and make sure that cool PR values are obtained, which are also quite easily interpreted.
If you see any inaccuracies or errors with me - please indicate in the comments or the message, and I will correct everything.
All code is compiled here:
PS: this whole idea is also easily implemented in other languages, at least in Python I did everything without difficulty.
My name is Aleksey. This time I broadcast from a workplace in ITAR-TASS.
In this short text, I'll introduce you to a method for calculating PageRank © (hereinafter will call it PR) on simple, clear examples, in the language of R. The algorithm is an intellectual property of Google, but, in view of its usefulness for data analysis tasks, apply a lot of public tasks , which can be reduced to the search for large nodes on the graph and ranking them by significance.
Mention of a large company in a post is not an advertisement.
Since I am not a professional mathematician, I use this article and this tutorial as a guide, and I recommend you .
Intuitive understanding of PR
Understanding how this works is not difficult. There is a set of elements that are interconnected. This is how they are related - this is a broad question: maybe through links (like Google’s), perhaps through references to each other (almost the same links), the probabilities of transitions between elements (the Markov process matrix) can be given a priori sense of communication. I would like to assign to these elements a certain criterion of importance, which would carry information about the probability that a given element will be visited by some abstract particle traveling along the graph in the diffusion process.
Um, that doesn't sound very clear. It's easier to imagine a guy for
This is due to the fact that some of the pages that he visits contain such interesting information in the original source, that other pages have to reprint it with an indication of the link.
This guy on Google was called Random surfer. It is a particle in the process of diffusion: a discrete change of position on a graph over time. And the probability with which he will visit the page with diffusion time tending to infinity is the PR.
Simple implementation of the calculation of PR
We agree - we work with 10 elements, in such a small, cozy graphchik.
# clear environment
rm(list = ls()); gc()
## load libs
library(data.table)
library(magrittr)
library(markovchain)
## dummy data
number_nodes <- 10
node_names <- letters[seq_len(number_nodes)]
set.seed(1)
nodes <- sapply(
seq_len(number_nodes), function(x)
{
paste(
c(
node_names[-x]
, sample(node_names[-x], sample(1:5, 1), replace = T)
)
, collapse = ' '
)
}
)
names(nodes) <- node_names
print(
paste(nodes, collapse = '; ')
)
## make long dt
dt <-
data.table(
citing_node = node_names
, cited_node = nodes
) %>%
.[, .(cited_node = unlist(strsplit(cited_node, ' '))), by = citing_node] %>%
dcast(
.
, cited_node ~ citing_node
, fun.aggregate = length
)
dt
apply(dt[,-1,with=F], 2, sum)
## affinity matrix
A <- as.matrix(dt[, 2:dim(dt)[2]])
A <- sweep(A, 2, colSums(A), `/`)
A[is.nan(A)] <- 0
rowSums(A)
colSums(A)
mark <- new("markovchain", transitionMatrix = t(A), states = node_names, name = "mark")
plot(mark)
Each of the 10 elements (nodes) contains from 10 to 14 references to other nodes in random order, excluding itself. At the moment, we just decide that these references are web links.
It is clear that it may happen that some of the elements are mentioned more often than others. Check it out.
By the way, I recommend using the data.table package for experiments. In conjunction with the principles of tidyverse, everything turns out efficiently and quickly.

This is our link matrix (usually called adjacency matrix in English).
The amount in each column is greater than zero, which means there is a connection from each element to any other element (this is important for further analysis).
> apply (dt [, - 1, with = F], 2, sum)
abcdefghij
11 14 10 10 11 11 11 11 11 12
We can create on the basis of this table the so-called Affinity matrix, or, in our opinion, the proximity matrix (and also call it the transition matrix), which mathematicians call the stochastic matrix (column-stochastic matrix): main source
Let's assign it to a variable with the name A.

Most the main thing now is that the sum in all columns is one.
> colSums (A)
abcdefghij
1 1 1 1 1 1 1 1 1 1 1
Here it is - the transition matrix, it is Markov, it is similar. Tsifir is the probability of transitions from an element in a column to an element in a line.
This, of course, is not real "similarity." These would be, for example, if you count the cosine of the angle between the presentation of documents. But it is important that the transition matrix is reduced to (pseudo-) probabilities, so that the sum for each column is equal to one.
Let's look at the Markov transition graph (our A):

Everything is approximately evenly confused). This is because we have given equiprobable transitions.
And now is the time of magic!
## calculate pagerank
ei <- eigen(A)
as.numeric(ei$values[1])
pr <- as.numeric(ei$vectors[,1] / sum(ei$vectors[,1]))
sum(pr)
names(pr) <- node_names
print(round(pr, 2))
For a stochastic matrix A, the first eigenvalue must be equal to one, and the corresponding eigenvector is the PageRank vector.
> print (round (pr, 2))
abcdefghij
0.09 0.11 0.09 0.10 0.10 0.11 0.10 0.11 0.08 0.11
This is the vector of PR values - this is the normalized eigenvector of the transition matrix A, corresponding to the eigenvalue of this matrix, equal to one, the dominant eigenvector.
Now you can rank the elements. But due to the nature of the experiment, they have a very similar weight.
Problems and their solutions using the power-method
The transition matrix A may not satisfy the conditions of stochasticity.
Firstly, there may be elements that do not refer to anywhere, that is, with the lack of feedback (they themselves can be referenced). For large real-life graphs, this is a very likely problem. This means that one of the columns of the matrix will have only zeros. In this case, the solution through eigenvectors will not work.
Google solved this problem by filling the column with a uniform probability distribution p = 1 / N. Where N is the number of all elements.
dim.1 <- dim(A)[1]
A <- as.data.table(A)
nul_cols <- apply(A, 2, function(x) sum(x) == 0)
if(
sum(nul_cols) > 0
)
{
A[
, (colnames(A)[nul_cols]) :=
lapply(.SD, function(x) 1 / dim.1)
, .SDcols = colnames(A)[nul_cols]
]
}
A <- as.matrix(A)
Secondly, in the graph there may be elements with feedback on each other, but not other elements of the graph. This is also an insurmountable problem for linear algebra due to the violation of assumptions.
It is solved by introducing a constant called the Damping factor, which denotes the a priori probability of transition from any element to any other, even if there are no physical references. In other words, diffusion is possible when it hits any state.
d = 0.15#damping factor (to ensure algorithm convergence)
M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrixIf we apply these transformations to our matrix, then it can again be solved through eigenvectors!
Thirdly, the matrix can be trivial, not square, and this is critical! I will not dwell on this moment, because I believe that you yourself will figure out how to fix it.
But there is a faster and more accurate method, which is also more economical in memory (which may be relevant for large graphs): Power method.
## pagerank function (tested on example from tutorial)
rm(pagerank_func)
pagerank_func <- function(
A #transition matrix
, eps = 0.00001#sufficiently small error
, d = 0.15#damping factor (to ensure algorithm convergence)
)
{
dim.1 <- dim(A)[1]
A <- as.data.table(A)
nul_cols <- apply(A, 2, function(x) sum(x) == 0)
if(
sum(nul_cols) > 0
)
{
A[
, (colnames(A)[nul_cols]) :=
lapply(.SD, function(x) 1 / dim.1)
, .SDcols = colnames(A)[nul_cols]
]
}
A <- as.matrix(A)
M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix
rank = as.numeric(rep(1 / dim.1, dim.1))
## iterate until convergencewhile(
sum(
(rank - M %*% rank) ^ 2
) > eps
)
{
rank <- M %*% rank
}
return(rank)
}
pr2 <- pagerank_func(A)
pr2=as.vector(pr2)
names(pr2)=node_names
Voila!
> print (round (pr, 2))
abcdefghij
0.09 0.11 0.09 0.10 0.10 0.11 0.10 0.11 0.08 0.11
> print (round (pr2, 2))
abcdefghij
0.09 0.11 0.09 0.10 0.10 0.11 0.10 0.11 0.08 0.11 0.11
On this I will finish the tutorial. Hope you find it useful.
I forgot to say that to build a transition matrix (probabilities) you can use the similarity of texts, the number of mentions, the fact that there is a link, and other metrics that are reduced to pseudo-probabilities or are probabilities. A rather interesting example is the ranking of sentences in the text on the matrix of similarity of the bags of the words tf-idf to highlight the sentence of the sum of all the text. There may be other creative uses of PR.
I recommend trying to play independently with the transition matrix and make sure that cool PR values are obtained, which are also quite easily interpreted.
If you see any inaccuracies or errors with me - please indicate in the comments or the message, and I will correct everything.
All code is compiled here:
Code
# clear environment
rm(list = ls()); gc()
## load libs
library(data.table)
library(magrittr)
library(markovchain)
## dummy data
number_nodes <- 10
node_names <- letters[seq_len(number_nodes)]
set.seed(1)
nodes <- sapply(
seq_len(number_nodes), function(x)
{
paste(
c(
node_names[-x]
, sample(node_names[-x], sample(1:5, 1), replace = T)
)
, collapse = ' '
)
}
)
names(nodes) <- node_names
print(
paste(nodes, collapse = '; ')
)
## make long dt
dt <-
data.table(
citing_node = node_names
, cited_node = nodes
) %>%
.[, .(cited_node = unlist(strsplit(cited_node, ' '))), by = citing_node] %>%
dcast(
.
, cited_node ~ citing_node
, fun.aggregate = length
)
dt
apply(dt[,-1,with=F], 2, sum)
## affinity matrix
A <- as.matrix(dt[, 2:dim(dt)[2]])
A <- sweep(A, 2, colSums(A), `/`)
A[is.nan(A)] <- 0
rowSums(A)
colSums(A)
mark <- new("markovchain", transitionMatrix = t(A), states = node_names, name = "mark")
plot(mark)
## calculate pagerank
ei <- eigen(A)
as.numeric(ei$values[1])
pr <- as.numeric(ei$vectors[,1] / sum(ei$vectors[,1]))
sum(pr)
names(pr) <- node_names
print(round(pr, 2))
## pagerank function (tested on example from tutorial)
rm(pagerank_func)
pagerank_func <- function(
A #transition matrix
, eps = 0.00001#sufficiently small error
, d = 0.15#damping factor (to ensure algorithm convergence)
)
{
dim.1 <- dim(A)[1]
A <- as.data.table(A)
nul_cols <- apply(A, 2, function(x) sum(x) == 0)
if(
sum(nul_cols) > 0
)
{
A[
, (colnames(A)[nul_cols]) :=
lapply(.SD, function(x) 1 / dim.1)
, .SDcols = colnames(A)[nul_cols]
]
}
A <- as.matrix(A)
M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix
rank = as.numeric(rep(1 / dim.1, dim.1))
## iterate until convergencewhile(
sum(
(rank - M %*% rank) ^ 2
) > eps
)
{
rank <- M %*% rank
}
return(rank)
}
pr2 <- pagerank_func(A)
pr2=as.vector(pr2)
names(pr2)=node_names
print(round(pr, 2))
print(round(pr2, 2))
PS: this whole idea is also easily implemented in other languages, at least in Python I did everything without difficulty.
