Delphi What is TDictionary

Good day.
But did you know that not all hash tables are equally useful? Now I’ll tell you a story, how one bad hash table ate all the performance, and did not frown. And how correcting this hash of the table accelerated the code by almost 10 times.
Of course, according to the topic - in the article we will talk about Delphi, but even if you are not a Delphi developer, I still advise you to look under the cut, and after reading the article in the source code, the hash of the tables that you use. And I advise Delphi developers to completely abandon the standard TDictionary.

1. How is the hash table.

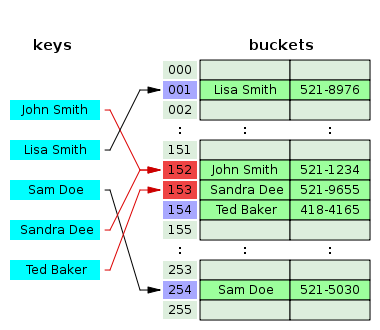
If you know very well how the hash of the table is arranged, and what linear probing is, you can safely proceed to the second part.

Any hash table inside is essentially an array. Elements of such an array are commonly called bucket s. And one of the central places in the hash table is the hash function. In general, a hash function is a function that maps one set to another of a fixed size set. And the task of any function hash is to give a uniformly distributed result on a fixed set. You can read more about hash functions on Wikipedia, I will not stop there.
So we prepared an array of say 10 bucket. Now we are ready to add the values ​​to our array. We take a hash from our key. For example, the hash turned out to be a 32 bit integer M. To determine in which bucket we will write our value - we take the remainder of the division: Index: = M mod 10 . And put in the bucket [Index]: = NewKeyValuePair .
Sooner or later, we will face the fact that some value will already lie in the bucket [Index]. And we will need to do something about it. This is called a Collision resolution . There are several collision resolution techniques. Here are the main ones:

Separate chaining or closed addressing

In the simplest case, this method represents this. Each bucket is a link to the head of a linked list . When a collision occurs, we simply add another element to the linked list. To prevent our list from degenerating into several linear linked lists, we introduce such a thing as a load factor . That is, when the number of elements by one bucket exceeds a certain number ( load factor ) - a new array of bucket-s is created, and all elements from the old are pushed to the new ones. The procedure is called rehash.
The disadvantages of this approach are that for each pair of <key, value> we create an object that must be added to the linked list.
This approach can be improved. For example, if instead of bucket-s you store a pair <key, value> + a link to the head of a linked list. By setting the load factor to 1 or even 0.75, you can practically avoid creating linked list items. And the bucket, which is an array, are very friendly placed on the processor cache. ps At the moment, I think this is the best way to resolve conflicts.

Open addressing

For this method, we have all the bucket-s - this is an array <key, value>, and absolutely all elements of the hash table are stored in bucket-s. One item per bucket. An attempt to insert an element into such a hash table is called probe . The most well-known sample methods are: Linear probing, Quadratic probing, Double hashing .
Let's see how Linear probing works.
Here we are in a situation where the bucket is already occupied by another element:

Then we simply add one to the bucket, and put the element in the next one:

Are you in the same bucket again? Now you have to step over as many as 3 elements:

But it turned out quite unsuccessfully:

According to the last example, it is clearly seen that in order for this method to be effective, it is necessary that there are a lot of free bucket-s, and it is also very important that the inserted elements do not stack in certain areas, which imposes high requirements on the hash function.
An attempt to bypass the failed hash function is Quadratic probing and Double hashing. The essence of Quadratic probing is that the next probe will be through 1, 2, 4, 8, etc. elements. The essence of Double hashing is that the hop size for the next probe is selected using a hash function. Either different from the first, or the same, but the hash is taken from the bucket index into which you just tried to put.
But the most important thing in Open addressing is that even if we fill in 10000 elements without a single collision, adding 10001 can lead to the fact that we will sort through all 10,000 elements already there. And the worst thing is that when we put this 10001th in order to turn to it later, we will again have to sort out 10,000 previous ones.
There is another unpleasant thing that follows from the foregoing. For Open addressing, the filling order is important. No matter how great the hash function is, everything can ruin the filling order. Let's look at the last case, we are out of luck. All elements were filled without a single collision, but the last element with a collision, which led to enumeration of a bunch of bucket-s:

What if we first put this single element:

we have a conflict, we went through only 1 bucket.
And then they would lay a neighbor:

they would again sort out 1 bucket.
And the next neighbor:

In total, the addition would lead to only one collision for each element. And although the total number of sorted bucket during addition would remain the same - it would generally become more balanced. And now, when accessing any element, we would do 2 checks in the bucket.

2. So what's wrong with Delphi with Linear probing in TDictionary?

After all, such a “failed” order with good hash function is difficult to obtain, you say? And make a big mistake.
In order to get all the elements of the TDictionary - we need to go through the array of buckets, and collect the elements in the occupied cells. The main catch here is that the sequence is preserved! Just create another TDictionary, and throw the data into it ... and get a bunch of collisions on the last elements before the next grow.
The simplest code to reproduce the situation:

    Hash1 := TDictionary<Integer, Integer>.Create();
    Hash2 := TDictionary<Integer, Integer>.Create();
    for i := 0to1280000do// этот TDictionary заполнится очень быстро
        Hash1.Add(i, i);
    for i in Hash1.Keys do// а этот - неожиданно медленнее, в десятки раз!
        Hash2.Add(i, i);

In TDictionary, rehash occurs only when there are less than 25% of free cells in the bucket array (Grow threshold = 75%). The increase in capacity always occurs 2 times. Here are the filled bucket in a large dictionary:

an attempt to add these elements to a smaller table can be considered as follows. Divide the large table into 2 parts. The first part will lie completely identical.

Now we need to add elements from the second half (green).

See how the number of collisions grows when you add the second half? And if rehash is still far away, and the table is large enough - we can get a huge overhead.
Let's count the number of collisions when adding a new element. To do this, I copied the source code for TDictionary, and added a couple of callback methods that return collisions. The results were plotted:

I filled the hash table with values, and as I filled it, I measured the number of collisions, every new N values ​​it displays a new pixel along the X axis. That is, the horizontal axis shows the filling of the table, and the vertical axis shows the number of collisions. To the right of each graph are the values:

• Max collision - the maximum number of collisions within one pixel along the X axis.
• Items per pixel - the number of elements per pixel of the graph along the X axis.
• Items count - total number of items in the hash table
• Filling percentage - the ratio of the number of elements to the number of bucket-s in the table.

The black line is the maximum number of collisions in a pixel. Red is the arithmetic mean of collisions in a pixel.
On the first chart, when filling 48%, everything is fine. The maximum of collisions is 169. As soon as we step over 50%, the worst thing begins. So at 61% comes the most joy. The number of collisions per element can reach 130 thousand! And so on up to 75%. After 75%, grow occurs and the percent filling decreases.
Each saw with a bunch of collisions - nothing like what I showed in the picture above. The “saw” ends with rehash and a sharp drop in collisions.
By chance, you may be at the top of such a saw, and an attempt to work with the last added elements will be accompanied by strong brakes.
How to fix this? Well, the most obvious option is to set the grow threshold to 50%. Those. free cells in the hash table must be at least 50%. Changing this threshold gives the following graphs:

on the same amounts of data. At the cost of additional memory, we “won” processor time. The problem here is that the GrowThreshold field is not accessible from the outside. You can also try to avoid unsuccessful sequences. Either manually shuffle / sort the data before placing it in the table, which is quite expensive, or create different tables with different hash functions. Many hash functions (such as Murmur2, BobJenkins hash) make it possible to set Seed / InitialValue. But choosing these values ​​at random is also not recommended. In most cases, a prime is suitable as seed, but still it is better to read the manual for a specific hash function.
And finally, my advice - do not use Open addressing as a universal method for any hash table. I think it's better to pay attention to Separate chaining with buckets <key, conception> + pointer to the head of a linked list with a load factor of about 0.75.

ps I spent several days searching for this pitfall. The situation was complicated by the fact that large amounts of data were difficult to profile + the dependence on% TD populate led to the fact that the brakes mysteriously disappeared periodically. So thank you for your attention, and I hope you do not stumble over it. ;)

upd 11.24.2016 In Rust, they stepped on the same rake: accidentallyquadratic.tumblr.com/post/153545455987/rust-hash-iteration-reinsertion

upd2 01/31/2017 And also in Swift:lemire.me/blog/2017/01/30/maps-and-sets-can-have-quadratic-time-performance