How to write a bloom filter in C ++
A Bloom filter is a data structure that can effectively determine if an element is a possible element of a set or definitely not related to it. This article will demonstrate a simple implementation of the Bloom filter in C ++.
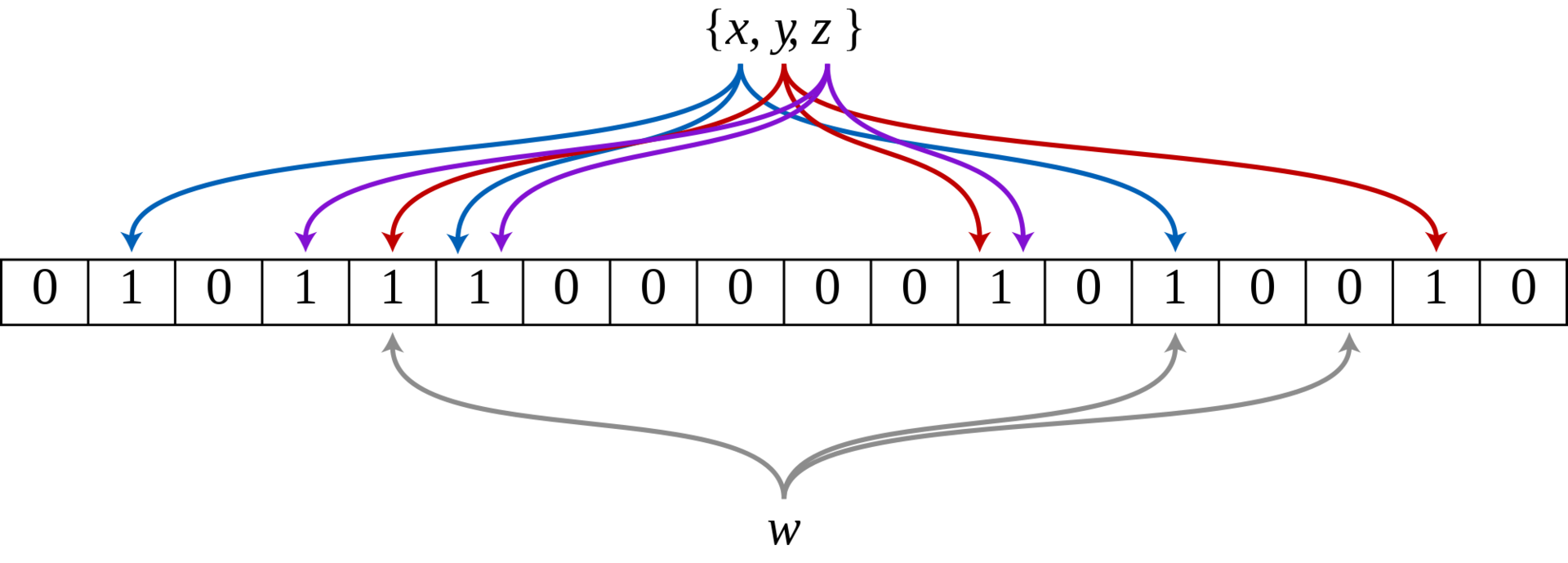
Let's first define the interface for this filter. Three main functions can be distinguished:
Several variables involved, including a small number of vectors, also contain the state of the filter.
It is worth noting that a much more efficient specialization requires only one bit per element (as opposed to one byte in typical implementations). You can process this structure according to the template, as an extension. Instead of hard coding key types and hash functions, we can process the class according to the template with something similar:
This allows the Bloom filter to be generalized to more complex data types.
There are two options for building a Bloom filter:
We can calculate the false positive error rate - n, based on the filter size - m, the number of hash functions - K and the number of nested elements -N, using the formula:

This formula is not very useful in this form. But we need to know how big the filter should be and how many hash functions it will take to use, given the estimated number of elements in the set and the error rate. There are two equations that we can use to calculate these parameters:

You may wonder how to implement kk hash functions; double hashing can be used to generate kk values of a hash function without affecting the probability of a false positive result! Such a result can be obtained using the formula, where i is the ordinal, m is the size of the Bloom filter, and x is the value to be hashed:

First you need to write a constructor. It just records the scaling parameters and the bitmap.
Next, let's write a function to calculate the 128-bit hash of this element. This implementation uses MurmurHash3 , a 128-bit hash function that has good trade-offs between performance, distribution, streaming behavior, and resistance to contradictions. Since this function generates a 128 bit hash and we need 2x64 bit hashes, we can split the returned hash in half to get the hash a (x) hash b (x).
Now that we have the hash values, we need to write a function to return the output signal n of the hash function.
All that remains to be done is to write functions for the set of control bits for the given elements.
Using a 4.3MB Bloom filter and 13 hash functions, inserting 1.8MB elements took approximately 189 nanoseconds for each element on an average laptop performance.
The original of this post can be found here .

Interface
Let's first define the interface for this filter. Three main functions can be distinguished:
- Constructor
- Function to add an element to a bloom filter
- Function to query whether an element is part of a bloom filter
Several variables involved, including a small number of vectors, also contain the state of the filter.
#include
struct BloomFilter {
BloomFilter(uint64_t size, uint8_t numHashes);
void add(const uint8_t *data, std::size_t len);
bool possiblyContains(const uint8_t *data, std::size_t len) const;
private:
uint64_t m_size;
uint8_t m_numHashes;
std::vector m_bits;
};
It is worth noting that a much more efficient specialization requires only one bit per element (as opposed to one byte in typical implementations). You can process this structure according to the template, as an extension. Instead of hard coding key types and hash functions, we can process the class according to the template with something similar:
std::vectorstd::vector,template< class Key, class Hash = std::hash >
struct BloomFilter {
...
};
This allows the Bloom filter to be generalized to more complex data types.
Bloom filter options
There are two options for building a Bloom filter:
- Filter Size in Bits
- The number of hash functions to use
We can calculate the false positive error rate - n, based on the filter size - m, the number of hash functions - K and the number of nested elements -N, using the formula:

This formula is not very useful in this form. But we need to know how big the filter should be and how many hash functions it will take to use, given the estimated number of elements in the set and the error rate. There are two equations that we can use to calculate these parameters:

Implementation
You may wonder how to implement kk hash functions; double hashing can be used to generate kk values of a hash function without affecting the probability of a false positive result! Such a result can be obtained using the formula, where i is the ordinal, m is the size of the Bloom filter, and x is the value to be hashed:

First you need to write a constructor. It just records the scaling parameters and the bitmap.
#include "BloomFilter.h"
#include "MurmurHash3.h"
BloomFilter::BloomFilter(uint64_t size, uint8_t numHashes)
: m_size(size),
m_numHashes(numHashes) {
m_bits.resize(size);
}
Next, let's write a function to calculate the 128-bit hash of this element. This implementation uses MurmurHash3 , a 128-bit hash function that has good trade-offs between performance, distribution, streaming behavior, and resistance to contradictions. Since this function generates a 128 bit hash and we need 2x64 bit hashes, we can split the returned hash in half to get the hash a (x) hash b (x).
std::array hash(const uint8_t *data,
std::size_t len) {
std::array hashValue;
MurmurHash3_x64_128(data, len, 0, hashValue.data());
return hashValue;
}
Now that we have the hash values, we need to write a function to return the output signal n of the hash function.
inline uint64_t nthHash(uint8_t n,
uint64_t hashA,
uint64_t hashB,
uint64_t filterSize) {
return (hashA + n * hashB) % filterSize;
}
All that remains to be done is to write functions for the set of control bits for the given elements.
void BloomFilter::add(const uint8_t *data, std::size_t len) {
auto hashValues = hash(data, len);
for (int n = 0; n < m_numHashes; n++) {
m_bits[nthHash(n, hashValues[0], hashValues[1], m_size)] = true;
}
}
bool BloomFilter::possiblyContains(const uint8_t *data, std::size_t len) const {
auto hashValues = hash(data, len);
for (int n = 0; n < m_numHashes; n++) {
if (!m_bits[nthHash(n, hashValues[0], hashValues[1], m_size)]) {
return false;
}
}
return true;
}
results
Using a 4.3MB Bloom filter and 13 hash functions, inserting 1.8MB elements took approximately 189 nanoseconds for each element on an average laptop performance.
The original of this post can be found here .
