What should we build a Zhegalkin polynomial ...
- Tutorial
I think everyone who has studied or is studying discrete mathematics at the university is familiar with the concept of the Zhegalkin polynomial .
The main feature of these polynomials is that any Boolean function can be represented by the Zhegalkin polynomial, and in a unique way.
Most often, to construct Zhegalkin polynomials, students are offered two methods for constructing such polynomials: the method of indefinite coefficients and the method of equivalent transformations.
Calculations using these methods are often cumbersome. Inattention to make a mistake is not difficult.
Under the cut is one convenient algorithm for constructing Zhegalkin polynomials, which students perceive with a bang, because It requires only the performance of "mechanical actions" without the use of any mental effort. A brief description of the method can be found on Wikipedia, but in my opinion it is not entirely clear on it how to quickly perform calculations. The method is known to me as the "Pascal Triangle Method".
The order of calculations is easier to show with an example. Next, I will show in steps what the calculation on paper should look like (or how convenient it is to carry out).
It is required to construct the Zhegalkin polynomial for the function f. As an example, we take the voting function as a function f%3Dx_1x_2%5Cvee%20x_2x_3%5Cvee%20x_1x_3%20%3D%20(00010111)) .
.
Step 1. We build a table of function values (the rows in the table are in ascending order of binary codes). It is better to place the table on the left side of the sheet.

Step 2. Building a triangle.
To do this, take the vector of the value of the function and write it opposite the first row of the table:

Next, fill the triangle, adding pairwise adjacent values modulo 2, write the result of the addition below.

We continue calculations until only one digit remains in the line.
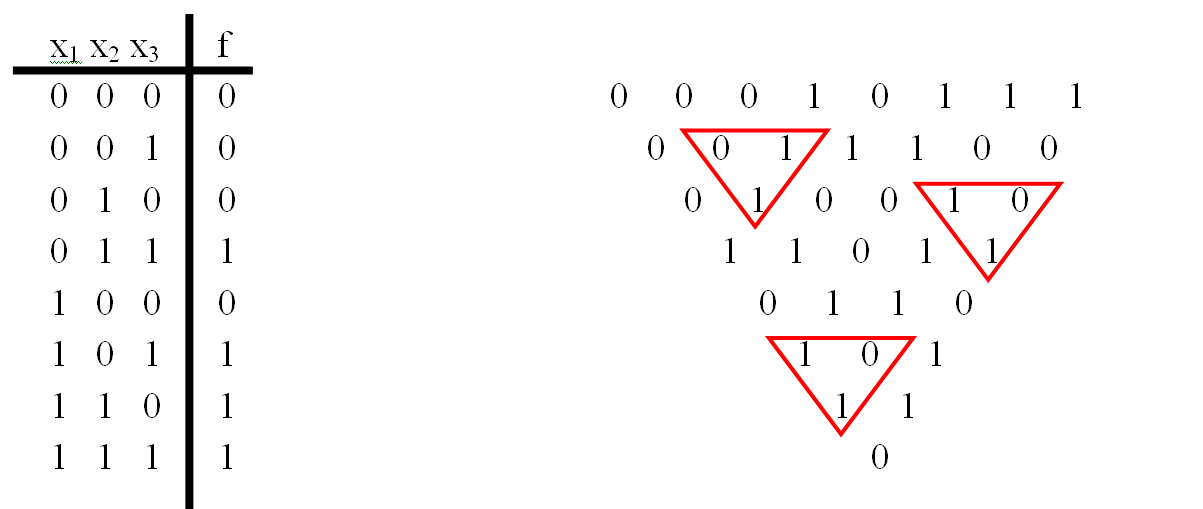
Step 3. Construction of the Zhegalkin polynomial.
We are interested in the left side of the triangle (the values are highlighted in bold):

The numbers on the left side (in bold) of the triangle are the coefficients of the polynomial for monotone conjunctions corresponding to sets of variable values.
Now let us write out these conjunctions for clarity. We write out the conjunctions using binary sets on the left side of the table according to the following principle: if the opposite of the variable xi is 1, then the variable is included in the conjunction; otherwise, the variable is not in the conjunction. The set (0,0,0) corresponds to constant 1.

If the principle of obtaining conjunctions is clear, then a column with them can be (even better) not written out, but immediately proceed to the construction of the polynomial.
To construct a polynomial, only conjunctions of rows with ones on the left side of the triangle are needed.
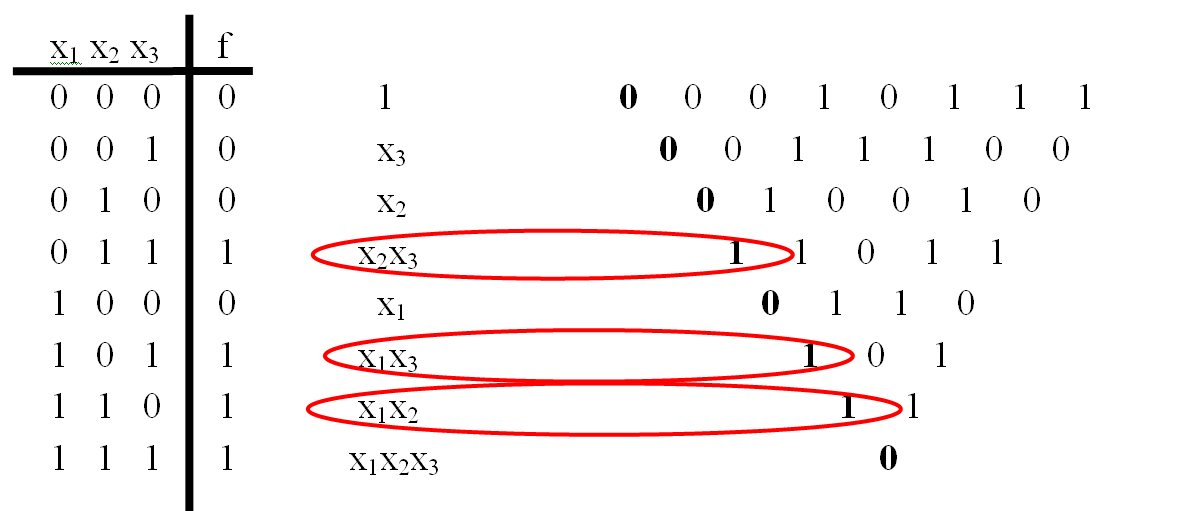
These are the conjunctions that make up the Zhegalkin polynomial. It remains only to write out the polynomial itself:
%3D%7B%7Bx%7D_%7B1%7D%7D%7B%7Bx%7D_%7B2%7D%7D%5Coplus%20%7B%7Bx%7D_%7B2%7D%7D%7B%7Bx%7D_%7B3%7D%7D%5Coplus%20%7B%7Bx%7D_%7B1%7D%7D%7B%7Bx%7D_%7B3%7D%7D.)
If the variables in the function are not 3, but 4 or more, then the method works without changes, only the size of the tables will increase. Nevertheless, unlike the method of uncertain coefficients, calculations can be performed without much effort on a sheet of paper.
Unfortunately, I could not find and see the source indicated on Wikipedia:
V.P. Suprun Tabular method of polynomial decomposition of Boolean functions // Cybernetics. - 1987. - No. 1. - S. 116-117.
The main feature of these polynomials is that any Boolean function can be represented by the Zhegalkin polynomial, and in a unique way.
Most often, to construct Zhegalkin polynomials, students are offered two methods for constructing such polynomials: the method of indefinite coefficients and the method of equivalent transformations.
Calculations using these methods are often cumbersome. Inattention to make a mistake is not difficult.
Under the cut is one convenient algorithm for constructing Zhegalkin polynomials, which students perceive with a bang, because It requires only the performance of "mechanical actions" without the use of any mental effort. A brief description of the method can be found on Wikipedia, but in my opinion it is not entirely clear on it how to quickly perform calculations. The method is known to me as the "Pascal Triangle Method".
The order of calculations is easier to show with an example. Next, I will show in steps what the calculation on paper should look like (or how convenient it is to carry out).
Pascal Triangle Method
It is required to construct the Zhegalkin polynomial for the function f. As an example, we take the voting function as a function f
Step 1. We build a table of function values (the rows in the table are in ascending order of binary codes). It is better to place the table on the left side of the sheet.

Step 2. Building a triangle.
To do this, take the vector of the value of the function and write it opposite the first row of the table:

Next, fill the triangle, adding pairwise adjacent values modulo 2, write the result of the addition below.

We continue calculations until only one digit remains in the line.

Step 3. Construction of the Zhegalkin polynomial.
We are interested in the left side of the triangle (the values are highlighted in bold):

The numbers on the left side (in bold) of the triangle are the coefficients of the polynomial for monotone conjunctions corresponding to sets of variable values.
Now let us write out these conjunctions for clarity. We write out the conjunctions using binary sets on the left side of the table according to the following principle: if the opposite of the variable xi is 1, then the variable is included in the conjunction; otherwise, the variable is not in the conjunction. The set (0,0,0) corresponds to constant 1.

If the principle of obtaining conjunctions is clear, then a column with them can be (even better) not written out, but immediately proceed to the construction of the polynomial.
To construct a polynomial, only conjunctions of rows with ones on the left side of the triangle are needed.

These are the conjunctions that make up the Zhegalkin polynomial. It remains only to write out the polynomial itself:
If the variables in the function are not 3, but 4 or more, then the method works without changes, only the size of the tables will increase. Nevertheless, unlike the method of uncertain coefficients, calculations can be performed without much effort on a sheet of paper.
Literature
Unfortunately, I could not find and see the source indicated on Wikipedia:
V.P. Suprun Tabular method of polynomial decomposition of Boolean functions // Cybernetics. - 1987. - No. 1. - S. 116-117.
