Entertaining mathematics. The most economical number system
We all know from the school course what the number system (SS) is. But not everyone thinks about how costly SS. Those. what set of numbers we need to represent the number in this CC. When we have a limited set of unique elements (multi-colored stones of different sizes) with which we can represent a number, what is the maximum number we can imagine using these elements? (all red pebbles are zero, green - one, blue - two, etc., small - zero discharge, medium - first, large - second, etc.). Where is the line at which the base of the SS plays a greater role than the digit capacity of the number?
Take for example n - the number of elements equal to 60. Breaking down the elements into 2 groups (binary number system) we get 30 digits. 30 units - at most 30-digit number with a base of 2. If we add 1 to it, we get a unit with 30 zeros, i.e. 2 in the 30th, since every zero is a power of two, and the digits start from 0, and we will not forget to subtract the one that was added.
For other SS similarly , where y is the maximum number, x is the base of the degree.
, where y is the maximum number, x is the base of the degree.
Construction points:
 .
.
 .
.





Graph of the function:
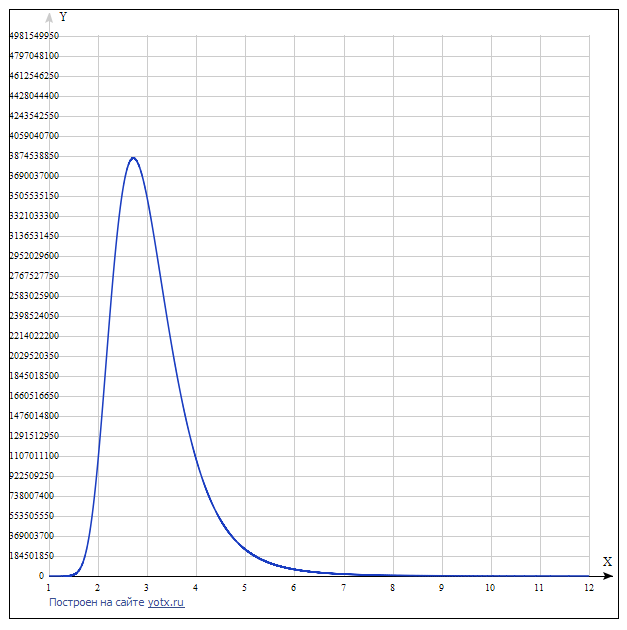
From the graph it is clear that with the increase in the base of the SS, starting from three, its cost increases and the function has an upper extremum. By bringing it to general appearance, you can get![$ y = (\ sqrt [x] x) ^ {n} -1 $](https://habrastorage.org/getpro/habr/formulas/759/8ad/ef6/7598adef600bb077d5798877d3f644cc.svg) , and the maximum function
, and the maximum function ![$ \ sqrt [x] x $](https://habrastorage.org/getpro/habr/formulas/fc9/4eb/725/fc94eb72542b934f8fdde50bd59e1e31.svg) achieved when
achieved when  .
.
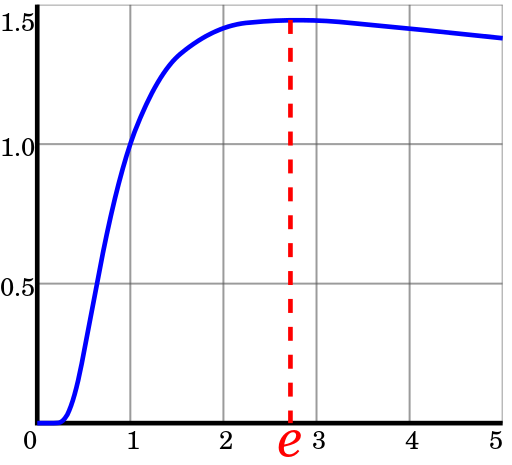
Function graph![$ y = \ sqrt [x] x $](https://habrastorage.org/getpro/habr/formulas/1d8/10b/bc3/1d810bbc3c1459b77d2888393e7739c3.svg)
Those. the most economical SS is the system as close as possible to or 3.
or 3.
PS: In addition to that, the SS with base 3 is odd, which means it has no rounding problem (lead 0.5 to 0 or 1), and if the numbers are written symmetrically (-1.0.1 instead of 0.1.2) then there is the simplicity of the representation of negative numbers (10-1 is 8, -101 is -8, where the minus is not a sign, but part of a number that can be replaced with Z), but this is a completely different arithmetic)))
Take for example n - the number of elements equal to 60. Breaking down the elements into 2 groups (binary number system) we get 30 digits. 30 units - at most 30-digit number with a base of 2. If we add 1 to it, we get a unit with 30 zeros, i.e. 2 in the 30th, since every zero is a power of two, and the digits start from 0, and we will not forget to subtract the one that was added.
For other SS similarly
Construction points:
Graph of the function:

From the graph it is clear that with the increase in the base of the SS, starting from three, its cost increases and the function has an upper extremum. By bringing it to general appearance, you can get

Function graph
Those. the most economical SS is the system as close as possible to
PS: In addition to that, the SS with base 3 is odd, which means it has no rounding problem (lead 0.5 to 0 or 1), and if the numbers are written symmetrically (-1.0.1 instead of 0.1.2) then there is the simplicity of the representation of negative numbers (10-1 is 8, -101 is -8, where the minus is not a sign, but part of a number that can be replaced with Z), but this is a completely different arithmetic)))
