Parallelizing the Strassen Algorithm on Intel® Xeon Phi (TM)
Intel Xeon Phi (TM) coprocessors are a PCI Express device and have an x86 architecture, providing high peak performance - up to 1.2 teraflops (trillion floating point operations per second) of double precision per coprocessor. Xeon Phi (TM) can handle up to 244 threads simultaneously, and this must be considered when programming for maximum efficiency.
Recently, together with Intel, we conducted a small study of the implementation efficiency of the Strassen algorithm for the Intel Xeon Phi (TM) coprocessor. Anyone interested in the intricacies of working with this device and just loving parallel programming, please, under cat.
The total number of operations of the standard algorithm for multiplying square matrices of size n (additions and multiplications):
The Strassen algorithm (1969), which relates to fast matrix multiplication algorithms, requires:
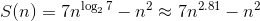
Thus, the Strassen algorithm has less asymptotic complexity and is potentially faster on large matrix sizes. But the recursive nature of this algorithm presents a certain complexity for efficient parallelization on modern computing systems and the use of data from memory.
In this paper, we consider a combined approach in which, upon reaching a threshold value, the standard matrix multiplication algorithm is called from the Strassen algorithm (we used Intel MKL DGEMM as the standard algorithm). This is due to the fact that with small matrix sizes (tens or hundreds, depending on the processor architecture), the Strassen algorithm starts to lose to the standard algorithm both in the number of operations and due to the larger number of cache misses. Theoretical estimates for the threshold matrix size for switching to the standard algorithm (excluding caching and pipelining) give different estimates - 8 for Hiheim and 12 for Hass-Lederman; in practice, the threshold value depends on the architecture of the computing system and should be estimated experimentally.
The results of computational experiments were compared with the DGEMM function from the Intel MKL library. We considered the multiplication of square size matrices
, where 
and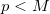 
. Here, M is understood as the threshold value of the size of the matrices, after which the standard algorithm is called. Multiplication of two matrices is written as 
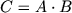where A, B and C are size matrices . The Strassen method for matrix multiplication is based on the recursive division of each matrix being multiplied by 4 submatrices and performing operations on them. The requirement to the size of the matrix ( and 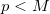) it is necessary to be able to divide each matrix 4 submatrices to the required depth of recursion.
The Strassen method is described by the following formula:
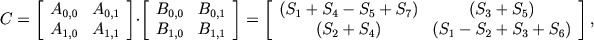
Where
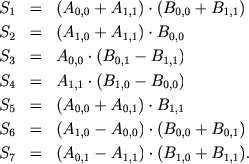
The following shows how you can distinguish 4 groups of operations, in each of them all operations can be performed in parallel.
There is nothing complicated in the implementation of parallelization. OpenMP and the task mechanism ( omp task ) were used, load balancing between tasks is shown in the figure. The first groups of operations were combined into one, so there are fewer synchronization points, since this is a very expensive operation.
To measure time, we used the standard approach with a “warming up” start and averaging the time of several starts. The Intel MKL dsecnd function is used as a timer.
After the implementation of parallelization, we conducted a series of tests. Tests were conducted in native mode on Intel Xeon Phi (TM) 7120D, 16 GB.
In order not to complicate the article, all tests will be carried out on a matrix size of 8192 × 8192 (this size is almost the maximum memory consumption for the parallel Strassen algorithm - about 10GB - and is large enough to experience the effect of less asymptotic complexity of the algorithm).
On a small number of threads, the Strassen algorithm was faster than Intel MKL DGEMM. It was also noted that on a large number of threads there is a drop in performance (the task almost does not scale more than 60 threads). For efficient use of Intel Xeon Phi (TM) resources in a multi-threaded application, it is recommended to use the number of threads that is a multiple of NP-1 , where NP is the number of processors in the device (in our case, 61). Read more here .
There was an idea that the use of parallelism inside the DGEMM called from Strassen could help further scaling. There are several functions for controlling the number of threads in MKL: mkl_set_num_threads , mkl_set_num_threads_local, mkl_domain_set_num_threads . When trying to use mkl_set_num_threads, we found that this function does not affect the number of threads in MKL DGEMM called from the Strassen algorithm (this function affected the number of threads in MKL outside of Strassen). Nested concurrency was enabled ( OMP_NESTED = true ).
As it turned out, MKL actively resists nested concurrency. MKL uses the MKL_DYNAMIC environment variable , which is true by default. This variable allows MKL to reduce the number of threads that the user sets, in particular when calling MKL functions from a parallel area, the number of threads will be forcibly set to 1. To enable parallelism in MKL DGEMM, we used the mkl_set_dynamic (0) function .
The results of the Strassen algorithm for 120 threads using multi-threaded MKL DGEMM were a little better, but we did not get a serious gain.
Our next step was to study the binding of OpenMP software threads to physical and logical kernels (binding). On Xeon Phi, the KMP_AFFINITY and KMP_PLACE_THREADS environment variables control the binding of threads to the kernels . Good description found here .
The most important among the KMP_AFFINITY parameters is type , which controls the order in which threads are assigned to the kernels (see the figure below).
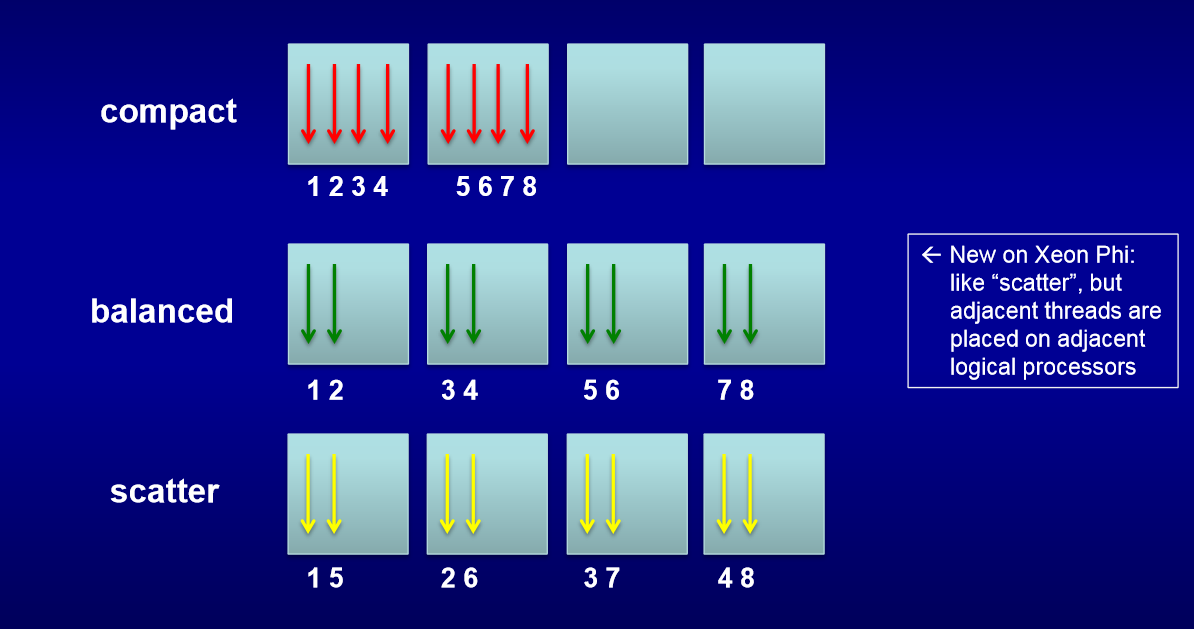
The following KMP_AFFINITY values were used :
KMP_AFFINITY = granularity = fine, balanced
KMP_AFFINITY = granularity = fine, compact
By default, the variable KMP_AFFINITY = granularity = core, balanced . During testing, it turned out that the best parameters for matrix multiplication are KMP_AFFINITY = granularity = fine, balanced , and this parameter affects the results of MKL DGEMM not so much as the Strassen algorithm, where, compared with KMP_AFFINITY = granularity = fine, compact, there is a two-fold reduction in time work. Also note that changing the KMP_AFFINITY environment variable from its default value ( KMP_AFFINITY = granularity = core, balanced ) reduced the MKL DGEMM runtime from a minimum of 1.90 s to 1.15 s (about 1.5 times). Results MKL DGEMM withcompact and balanced differ in a predictable way, for example, with 120 threads, the compact version uses 30 cores of 4 threads each , and balanced - 60 of 2 cores, due to the larger number of cores, and almost double acceleration in the balanced version is obtained .
We also tried to profile the program on Xeon Phi, how to do this can be read here . To profile only the multiplication algorithm, we used the capabilities of the VTune API .
As a result, we were unable to catch up with MKL DGEMM on the maximum number of threads, but learned a little more about programming such a powerful computer as Intel Xeon Phi (TM).
Recently, together with Intel, we conducted a small study of the implementation efficiency of the Strassen algorithm for the Intel Xeon Phi (TM) coprocessor. Anyone interested in the intricacies of working with this device and just loving parallel programming, please, under cat.
The total number of operations of the standard algorithm for multiplying square matrices of size n (additions and multiplications):
The Strassen algorithm (1969), which relates to fast matrix multiplication algorithms, requires:
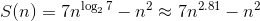
Thus, the Strassen algorithm has less asymptotic complexity and is potentially faster on large matrix sizes. But the recursive nature of this algorithm presents a certain complexity for efficient parallelization on modern computing systems and the use of data from memory.
In this paper, we consider a combined approach in which, upon reaching a threshold value, the standard matrix multiplication algorithm is called from the Strassen algorithm (we used Intel MKL DGEMM as the standard algorithm). This is due to the fact that with small matrix sizes (tens or hundreds, depending on the processor architecture), the Strassen algorithm starts to lose to the standard algorithm both in the number of operations and due to the larger number of cache misses. Theoretical estimates for the threshold matrix size for switching to the standard algorithm (excluding caching and pipelining) give different estimates - 8 for Hiheim and 12 for Hass-Lederman; in practice, the threshold value depends on the architecture of the computing system and should be estimated experimentally.
The results of computational experiments were compared with the DGEMM function from the Intel MKL library. We considered the multiplication of square size matrices
, where and 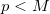. Here, M is understood as the threshold value of the size of the matrices, after which the standard algorithm is called. Multiplication of two matrices is written as 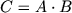where A, B and C are size matrices . The Strassen method for matrix multiplication is based on the recursive division of each matrix being multiplied by 4 submatrices and performing operations on them. The requirement to the size of the matrix ( and 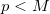) it is necessary to be able to divide each matrix 4 submatrices to the required depth of recursion. The Strassen method is described by the following formula:
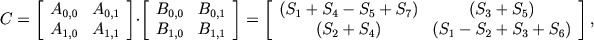
Where
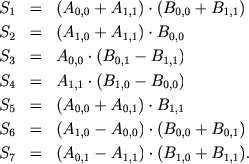
The following shows how you can distinguish 4 groups of operations, in each of them all operations can be performed in parallel.
There is nothing complicated in the implementation of parallelization. OpenMP and the task mechanism ( omp task ) were used, load balancing between tasks is shown in the figure. The first groups of operations were combined into one, so there are fewer synchronization points, since this is a very expensive operation.
To measure time, we used the standard approach with a “warming up” start and averaging the time of several starts. The Intel MKL dsecnd function is used as a timer.
function for measuring the operating time of multiplication algorithms
double run_method(MatrixMultiplicationMethod mm_method, int n, double *A, double *B, double *C)
{
int runs = 5;
mm_method(n, A, B, C);
double start_time = dsecnd();
for (int i = 0; i < runs; ++i)
mm_method(n, A, B, C);
double end_time = dsecnd();
double elapsed_time = (end_time - start_time) / runs;
return elapsed_time;
}
After the implementation of parallelization, we conducted a series of tests. Tests were conducted in native mode on Intel Xeon Phi (TM) 7120D, 16 GB.
what Xeon Phi (TM) and usage modes are still there
| Name | TDP (WATTS) | Number of cores | Frequency (GHz) | Peak Performance (GFLOP) | Peak Throughput (GB / s) | Memory capacity (GB) |
| 3120A | 300 | 57 | 1.1 | 1003 | 240 | 6 |
| 3120P | 300 | 57 | 1.1 | 1003 | 240 | 6 |
| 5110P | 225 | 60 | 1.053 | 1011 | 320 | 8 |
| 5120D | 245 | 60 | 1.053 | 1011 | 352 | 8 |
| 7120P | 300 | 61 | 1.238 | 1208 | 352 | 16 |
| 7120X | 300 | 61 | 1.238 | 1208 | 352 | 16 |
| 7120A | 300 | 61 | 1.238 | 1208 | 352 | 16 |
| 7120D | 270 | 61 | 1.238 | 1208 | 352 | 16 |
 |  |  |
| Suitable for highly parallel and vectorized code; serial code runs slowly | Suitable for serial code with large parallel regions, a potential problem is PCIe data transfer | Suitable for highly parallel code that runs efficiently on both platforms, a potential problem is load imbalance |
In order not to complicate the article, all tests will be carried out on a matrix size of 8192 × 8192 (this size is almost the maximum memory consumption for the parallel Strassen algorithm - about 10GB - and is large enough to experience the effect of less asymptotic complexity of the algorithm).
| Number of threads | 1 | 4 | 8 | 16 | 60 | 120 | 180 | 240 |
| Strassen, with | 114.89 | 29.9 | 15.75 | 8.85 | 3.68 | 3.58 | 4.22 | 8.17 |
| MKL DGEMM, c | 131.79 | 34.38 | 17.27 | 9 | 2.61 | 1.90 | 2.45 | 2.54 |
On a small number of threads, the Strassen algorithm was faster than Intel MKL DGEMM. It was also noted that on a large number of threads there is a drop in performance (the task almost does not scale more than 60 threads). For efficient use of Intel Xeon Phi (TM) resources in a multi-threaded application, it is recommended to use the number of threads that is a multiple of NP-1 , where NP is the number of processors in the device (in our case, 61). Read more here .
There was an idea that the use of parallelism inside the DGEMM called from Strassen could help further scaling. There are several functions for controlling the number of threads in MKL: mkl_set_num_threads , mkl_set_num_threads_local, mkl_domain_set_num_threads . When trying to use mkl_set_num_threads, we found that this function does not affect the number of threads in MKL DGEMM called from the Strassen algorithm (this function affected the number of threads in MKL outside of Strassen). Nested concurrency was enabled ( OMP_NESTED = true ).
As it turned out, MKL actively resists nested concurrency. MKL uses the MKL_DYNAMIC environment variable , which is true by default. This variable allows MKL to reduce the number of threads that the user sets, in particular when calling MKL functions from a parallel area, the number of threads will be forcibly set to 1. To enable parallelism in MKL DGEMM, we used the mkl_set_dynamic (0) function .
code of what we got
mkl_set_dynamic(0);
omp_set_nested(1);
set_num_threads(num_threads);
mkl_set_num_threads(mkl_num_threads);
strassen( … );
…
mkl_set_num_threads(num_threads * mkl_num_threads);
dgemm( … );
| Total number of threads | Strassen, with | MKL DGEMM, s | ||
| Number of threads in MKL DGEMM | ||||
| 1 | 2 | 4 | ||
| 60 | 3.68 | 3.89 | 5.19 | 2.61 |
| 120 | 3.58 | 3.50 | 3.82 | 1.90 |
| 240 | 8.17 | 4.23 | 3.59 | 2.54 |
The results of the Strassen algorithm for 120 threads using multi-threaded MKL DGEMM were a little better, but we did not get a serious gain.
Our next step was to study the binding of OpenMP software threads to physical and logical kernels (binding). On Xeon Phi, the KMP_AFFINITY and KMP_PLACE_THREADS environment variables control the binding of threads to the kernels . Good description found here .
The most important among the KMP_AFFINITY parameters is type , which controls the order in which threads are assigned to the kernels (see the figure below).
The following KMP_AFFINITY values were used :
KMP_AFFINITY = granularity = fine, balanced
| Total number of threads | Strassen, with | MKL DGEMM, s | ||
| Number of threads in MKL DGEMM | ||||
| 1 | 2 | 4 | ||
| 60 | 3.67 | 4.07 | 5.53 | 2.64 |
| 120 | 3.54 | 3.51 | 3.95 | 1.51 |
| 240 | 7.11 | 4.33 | 3.41 | 1.15 |
KMP_AFFINITY = granularity = fine, compact
| Total number of threads | Strassen, with | MKL DGEMM, s | ||
| Number of threads in MKL DGEMM | ||||
| 1 | 2 | 4 | ||
| 60 | 9.29 | 9.96 | 10.27 | 4.58 |
| 120 | 6.23 | 6.79 | 6.04 | 2.31 |
| 240 | 9.32 | 5.21 | 4.21 | 1.15 |
By default, the variable KMP_AFFINITY = granularity = core, balanced . During testing, it turned out that the best parameters for matrix multiplication are KMP_AFFINITY = granularity = fine, balanced , and this parameter affects the results of MKL DGEMM not so much as the Strassen algorithm, where, compared with KMP_AFFINITY = granularity = fine, compact, there is a two-fold reduction in time work. Also note that changing the KMP_AFFINITY environment variable from its default value ( KMP_AFFINITY = granularity = core, balanced ) reduced the MKL DGEMM runtime from a minimum of 1.90 s to 1.15 s (about 1.5 times). Results MKL DGEMM withcompact and balanced differ in a predictable way, for example, with 120 threads, the compact version uses 30 cores of 4 threads each , and balanced - 60 of 2 cores, due to the larger number of cores, and almost double acceleration in the balanced version is obtained .
We also tried to profile the program on Xeon Phi, how to do this can be read here . To profile only the multiplication algorithm, we used the capabilities of the VTune API .
As a result, we were unable to catch up with MKL DGEMM on the maximum number of threads, but learned a little more about programming such a powerful computer as Intel Xeon Phi (TM).