Modeling a dipole antenna in openEMS

In the previous part, we described how to model the propagation of
electromagnetic waves using the openEMS simulator . Now consider how to calculate something useful. We model a dipole half-wave antenna at a frequency of 500 MHz. Modeling in the frequency domain and antenna pattern modeling will be considered. A diagram of this antenna is shown in the figure.



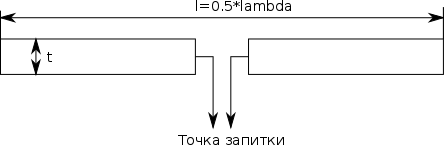
A dipole antenna consists of two beams, each of which has a length equal to 1/4 wave for the resonant frequency. The antenna is fed from the center. The antenna has a resistance at a resonance frequency equal to approximately 75 Ohms and a directivity diagram in the shape of a torus. More information on the theory of operation of a dipole antenna can be found, for example, in the textbook of Eisenberg or Belotserkovsky. We should get these results after modeling.

Below the cat is a script with a model of a dipole antenna with line-by-line parsing. It is assumed that the reader is familiar with the basics of Matlab / Octave, electrical engineering and antenna theory (knows what the complex resistance, S-parameters and SWR are).

For those who are not aware of what is happening here, links to my previous articles:

• openEMS - open source electromagnetic simulator
• OpenEMS modeling basics

The simulation script must first be saved to a text file with the * .m extension using your favorite test editor (for example, KWrite). Then you need to run Octave from the command line, passing it the script name as a parameter. Suppose, if our script is called dipole.m, then the simulation starts like this:

octave dipole.m

If you want to use the graph view from Octave in interactive mode, you must first run Octave from the command line, and then use the source command. It will load the dipole.m script from the current directory.

source dipole.m

As a result of modeling, we want to get:

• Dependence of the input impedance of the antenna to the power points on the frequency.
• The dependence of the SWR antenna at the power point on the frequency for a 50 ohm source
• DN in polar coordinates
• 3D MD in spherical coordinates

Let's proceed to line-by-line parsing of the script. The openEMS documentation suffers from spaces, so I had to think up something myself.

So at the beginning of the script we clear all the variables:

close all;
clear;
clc;

Now you need to declare the name of the XML file that contains the simulation task and the temporary directory in which the simulation results will be stored. Files with the calculation results reach 100 MB, so you need to take care of the disk space.

physical_constants
SimPath = 'tmp';
SimCSX = 'tmp.xml';

Now we begin the description of the parametric antenna model. This means that when changing parameters (for example, the calculated resonant frequency), Matlab / Octave will automatically recalculate all antenna sizes. The grid step is chosen equal to 1/50 of the wavelength.

f_max = 0.5e9; # расчётная частота резонанса
lambda = c0/f_max; # длина волны
step=lambda/50; # шаг сетки

As you remember from physics, the wavelength and frequency are connected through the speed of light
c0

We declare the simulation space (SimBox) - a cube with an edge equal to
twice the wavelength (2 * lambda). Fill the space with
mesh.

CSX = InitCSX();
mesh.x = -lambda:step:lambda;
mesh.y = -lambda:step:lambda;
mesh.z = -lambda:step:lambda;
SimBox = [2*lambda 2*lambda 2*lambda];
CSX = DefineRectGrid(CSX,1,mesh);

Now we set the source of excitation. In the last part, we used a fixed frequency sinusoidal source. openEMS first performs the calculation in the time domain, and then recounts the result in the frequency domain. Therefore, in order to simulate the frequency properties of a system, a source with an extended spectrum is needed. A Gaussian impulse is available as such a source in openEMS.

So first, we declare the variables in which we will store the parameters of the Gaussian pulse. It is necessary to set the center frequency of the spectrum of the Gaussian pulse and half the width of the spectrum. We will simulate our antenna in the frequency range from 200 MHz to 600 MHz. Therefore, the center frequency will be 400 MHz, and the spectrum width + -200 MHz from the center frequency.

f0 = 400e6;
fc = 0.5*f0;
FDTD = InitFDTD('NrTS',30000);
FDTD = SetGaussExcite(FDTD,f0,fc);

The FDTD space is initialized using the InitFDTD () function. The second parameter is to pass the number of samples in the time domain. It must be selected in such a way that it exceeds the pulse duration in the sampling steps. Usually 30,000 is enough. Otherwise, we get an error message that says that the calculation interval is less than the duration of the Gaussian pulse.

Now we need to set the boundary conditions. We simulate the antenna in free space, so it will be surrounded on all sides by a completely absorbing MUR dielectric:

BC = {'MUR','MUR','MUR','MUR','MUR','MUR'};
FDTD = SetBoundaryCond(FDTD,BC);

Now declare the geometry. The process of describing the geometry for those who are familiar with HFSS, for example, looks unusual and unusual.

The dipole will consist of two conductive parallelepipeds, between which an excitation source is connected. The thickness of the rays of the dipole may be less than the grid pitch. According to the theory, the greater the thickness of the dipole antenna, the wider its bandwidth. All our geometry is parametrized and will be automatically recounted when the parameters change. This is the advantage of the simulator built into Matlab / Octave.

t = step/4; # толщина луча диполя (1/200 длины волны)
CSX = AddMetal(CSX,'right_beam'); # правая половинка диполя
start = [t -t -t]; # начальная точка
stop = [lambda/4 t t]; # конечная точка
CSX = AddBox(CSX,'right_beam',1,start,stop); # строим параллелепипед из металла

The coordinates of points in space are set in openEMS as a matrix-row of three components that follow in the order [xyz].

The AddMetal () function adds some metal object. The created object must be associated with some geometric object. The AddBox () function adds a box. The penultimate and last parameters are the coordinates of its extreme vertices. The third parameter is priority. His appointment remains unclear to me. You can always set it to 1. The second parameter is the name of the parallelepiped material object. We must use the object 'right_beam' that we created earlier.

Similar actions for the left ray:

CSX = AddMetal(CSX,'left_beam');
start = [0 -t -t];
stop = [-lambda/4 t t];
CSX = AddBox(CSX,'left_beam',1,start,stop);

Now you need to power the antenna. To power the antenna, a special object called the Lumped Port is used.

There is still a distributed port, which is a region of space from which EMW propagates. The distributed port was used in the second part.

We need to use a regular port. It corresponds to the case of powering the antenna from a voltage source. The Gaussian impulse announced earlier is the voltage source. The port represents two points in space between which the terminals of the virtual voltage source are connected. First we declare these two points. They should lie on the surface of the dipole rays:

start = [0 0 0 ]; # сюда подключаем порт
stop = [step 0 0];

Now declare the output impedance of the source:

R = 50;

And you can add the port itself:

[CSX  port] = AddLumpedPort(CSX,1,1,R,start,stop,[1 0 0],true);

The AddLumpedPort () function has 8 parameters. Let's consider them in more detail:

• The second parameter is priority. Can be put in 1
• The third parameter is the serial number of the port. There may be several
  ports.
• The fourth parameter is the output impedance of the source
• Fifth and sixth parameters - port connection points
• The seventh parameter is the direction of the signal. A vector of three components
  that shows the direction of the signal in the format [xyz]. Our
  signal is directed along the X axis.

Now you need to specify the area in which the field emitted by the antenna will be calculated. openEMS calculates the field in the near field, and then, using the NF2FF post processor, recalculates it into the field in the far zone. The antenna bottom is calculated from the field in the far zone. The area in which the field is calculated must be taken equal to the modeling area, be sure to step back a few steps of the grid from the boundary.

SimBox = SimBox-step*4.0; # отступаем от границы
[CSX nf2ff] = CreateNF2FFBox(CSX,'nf2ff',-SimBox/2,SimBox/2);

All! The geometry is set. You can record the job file for openEMS and see the result in the interactive viewer AppCSXCAD.

mkdir('tmp');
SimPath = 'tmp/tmp.xml'
WriteOpenEMS(SimPath,FDTD,CSX);
CSXGeomPlot(SimPath);

If everything was done correctly, then we will see the following picture (the port is visible in the dipole gap):



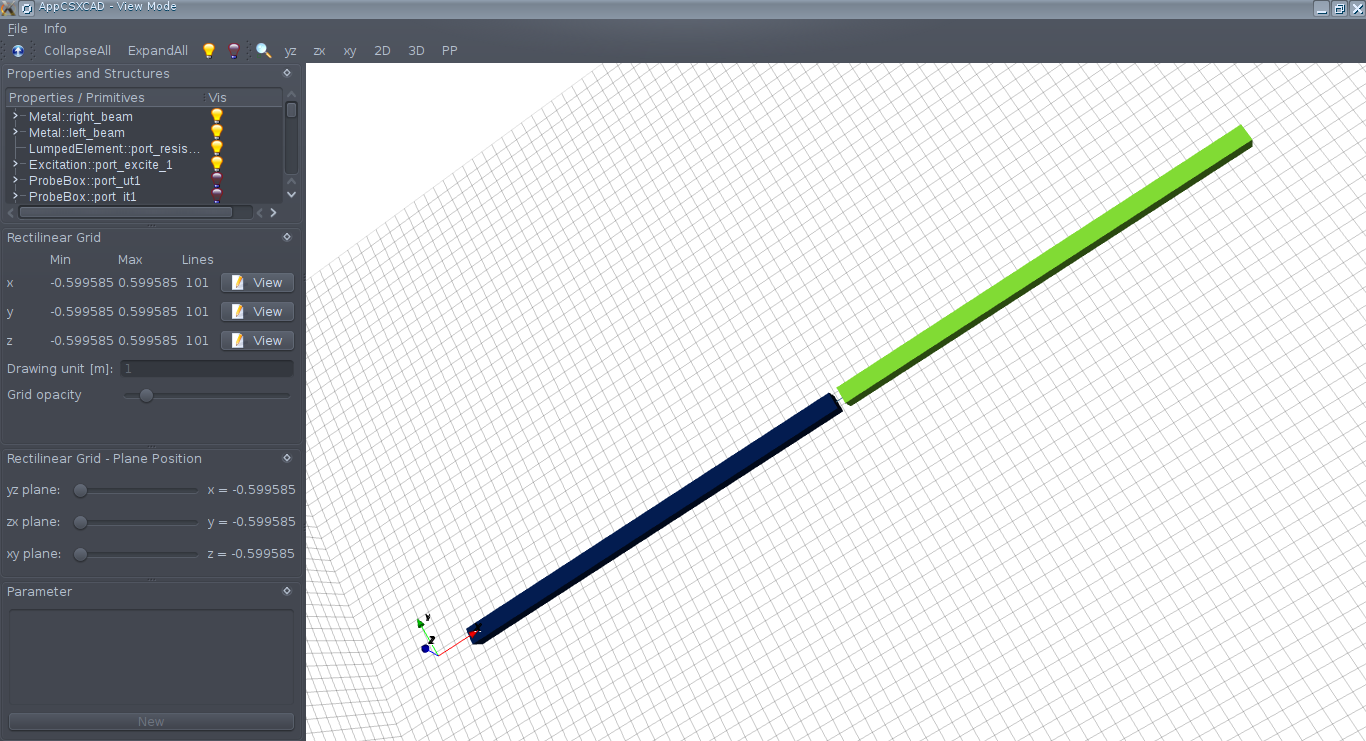
Now we run openEMS.

RunOpenEMS('tmp','tmp.xml');

The calculation has been going on for quite some time. After calculation, they are created for the structure:

• port - contains information about the characteristics of the antenna in the
  frequency domain
• nf2ff - contains information about the antenna pattern

We need to extract information about the antenna input impedance and reflection coefficient S11 from the port structure. To do this, you need the following fields in the
port structure :

• port.uf.tot - Total voltage at the port terminals
• port.if.tot - Total current flowing through the port
• port.uf.inc - The amplitude of the incident wave voltage
• port.uf.ref - The amplitude of the reflected wave voltage

Now with the help of formulas known from the course of radio engineering, we calculate the input resistance Zin and the reflection coefficient at the input S11 (it can be converted into
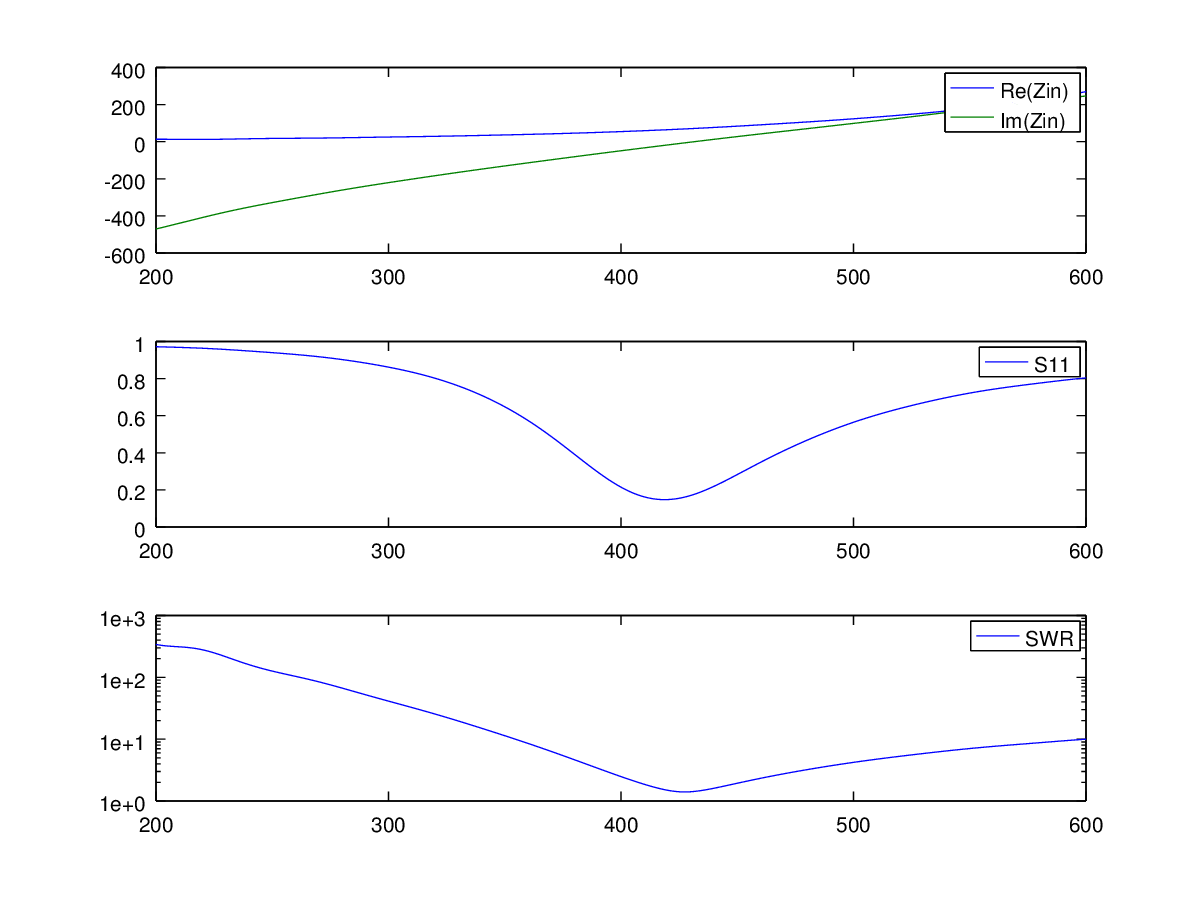
a standing wave coefficient - SWR). Now you can cut the graphs of Zin (active and reactive parts), SWR and S11 using standard Matlab / Octave tools. This piece of code requires no explanation.

freq = linspace(f0-fc,f0+fc,501); # ось частот
port = calcPort(port,'tmp',freq); # извлекаем параметры
Zin = port.uf.tot ./ port.if.tot;
S11 = port.uf.ref ./ port.uf.inc;
subplot(3,1,1);
plot(freq/1e6,real(Zin),freq/1e6,imag(Zin)); # строим графики Rвх и Xвх
legend('Re(Zin)','Im(Zin)');
subplot(3,1,2);
plot(freq/1e6,S11); # строим график S11
swr = (1+abs(S11))./(1-abs(S11)); # найдём точку минимального КСВ
[swr_min idx] = min(swr);
[Xmin idx1] = min(abs(imag(Zin))); # и точку резонанса
fr = freq(idx);
fr1 = freq(idx1);
Zr = Zin(idx);
Zr1 = Zin(idx1);
disp("Minimum SWR frequency:"); # выведем параметры антенны
disp(fr);
disp("Resonant frequency (jX=0)");
disp(fr1);
disp("Impedance at minimum SWR");
disp(Zr);
disp("Impedance at resonant frequency");
disp(Zr1);
disp("Minimum SWR:");
disp(swr_min);
subplot(3,1,3);
semilogy(freq/1e6,swr);

We get the following antenna parameters. It can be seen that the resonance frequency went down from the calculated one. The antenna resistance at a resonance of 71.2 Ohms is almost like in textbooks, the deviation is caused by the thickness of the dipole.

Minimum SWR frequency:
 427200000
Resonant frequency (jX=0)
 431200000
Impedance at minimum SWR
 68.7692 -  6.5511i
Impedance at resonant frequency
 71.18555 -  0.45064i
Minimum SWR:
 1.4013
 

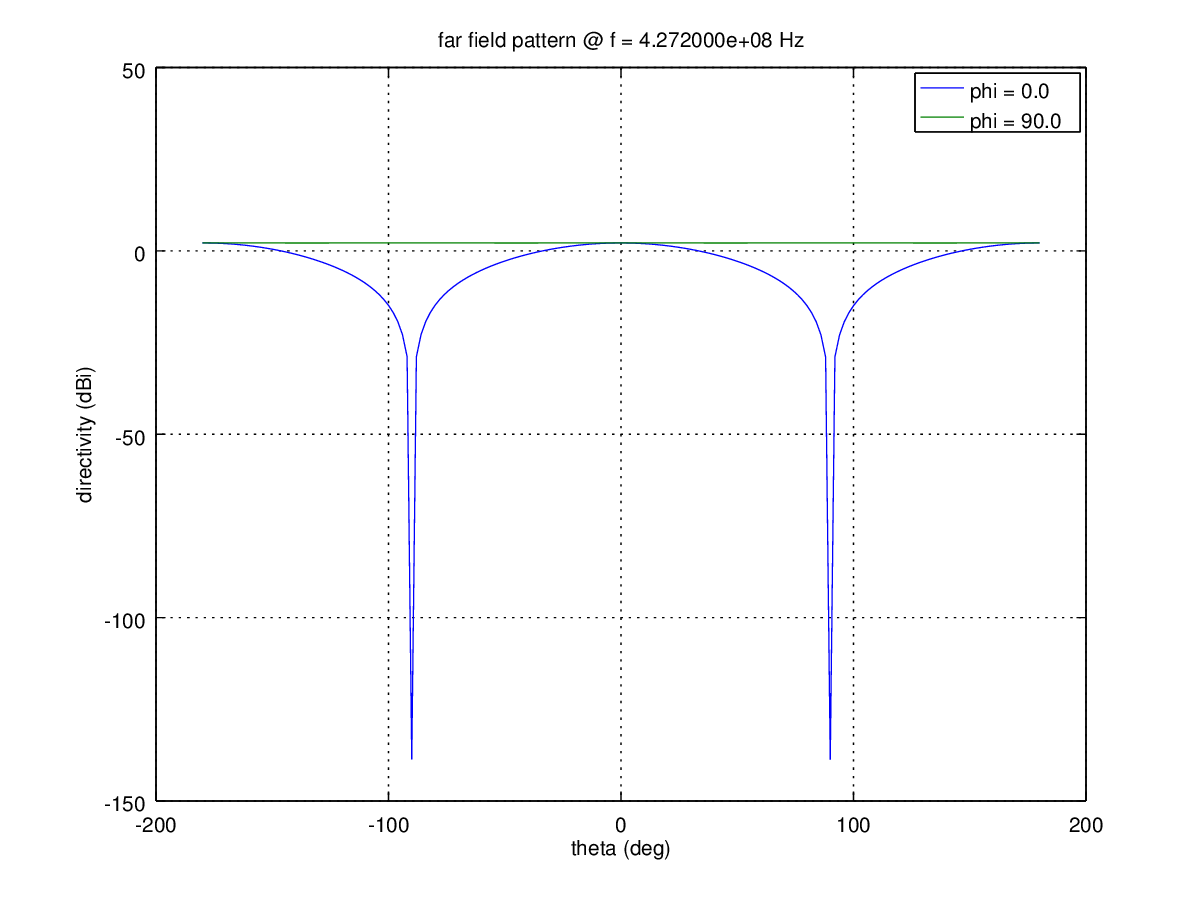
Now we calculate the DN in polar coordinates. The last two parameters of the CalcNF2FF () function are the range of angles within which the DN is considered. The third parameter, she needs to pass the frequency at which the DN is calculated.
We get the following graphs:

nf2ff = CalcNF2FF(nf2ff,'tmp',fr,[-180:2:180]*pi/180,[0 90]*pi/180);
figure
polarFF(nf2ff,'xaxis','theta','param',[1 2],'normalize',1);

MD in Cartesian coordinates:

figure
plotFFdB(nf2ff,'xaxis','theta','param',[1 2]);

thetaRange = (0:2:180);
phiRange=(0:2:360)-180;
nf2ff = 
CalcNF2FF(nf2ff,'tmp',fr,thetaRange*pi/180,phiRange*pi/180,'Verbose',1,'Outfile'
,'3D_Pattern.h5');
figure
plotFF3D(nf2ff,'logscale',-20);

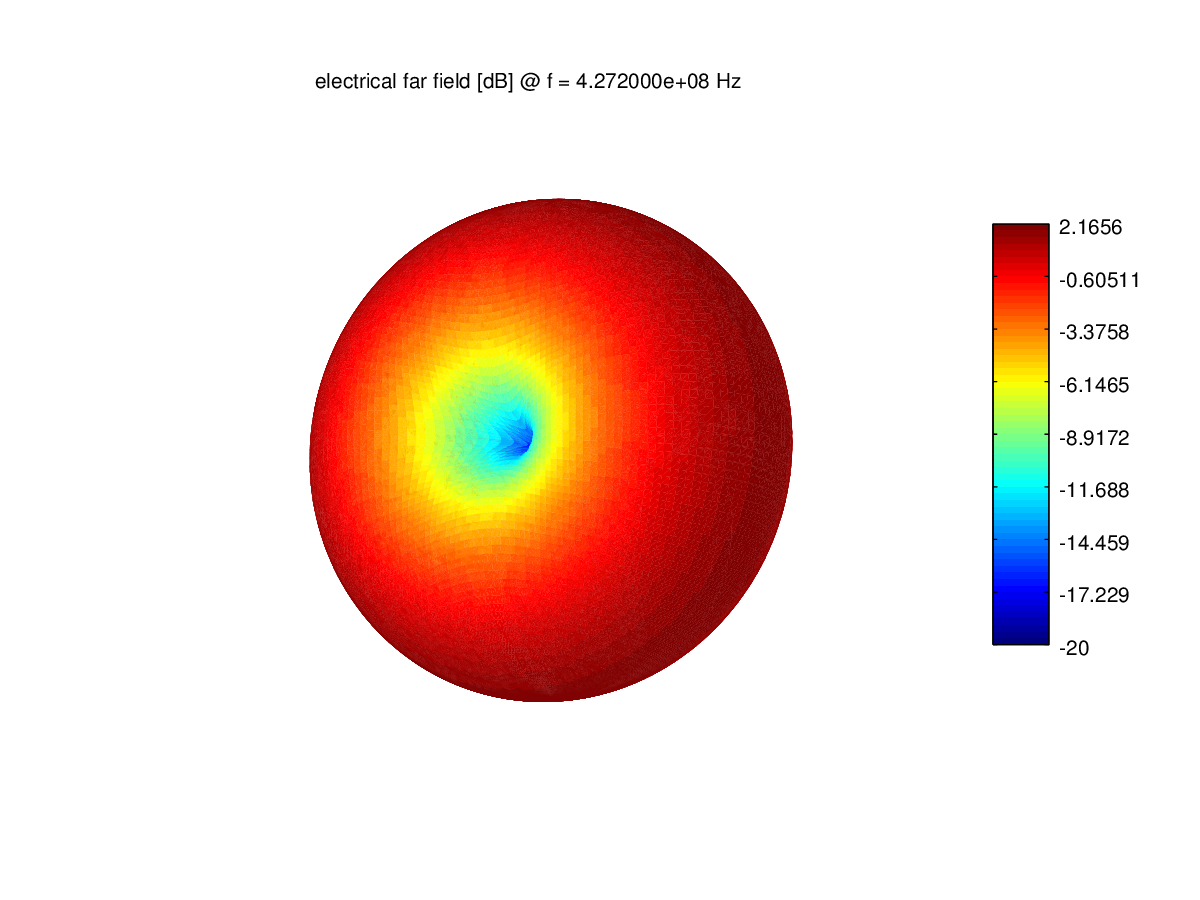
Spatial DN has the form of a torus, as in textbooks on antennas. The
gain of the antenna is 2.1 dB.

You can also create a * .vtk file so that you can later view it with Paraview:

E_far_normalized = nf2ff.E_norm{1} / max(nf2ff.E_norm{1}(:)) * nf2ff.Dmax;
DumpFF2VTK(['tmp/3D_Pattern.vtk'],E_far_normalized,thetaRange,phiRange,'scale',
1e-3);

This is how the NAM looks in Paraview (you need to open the 3D_Pattern.vtk file):



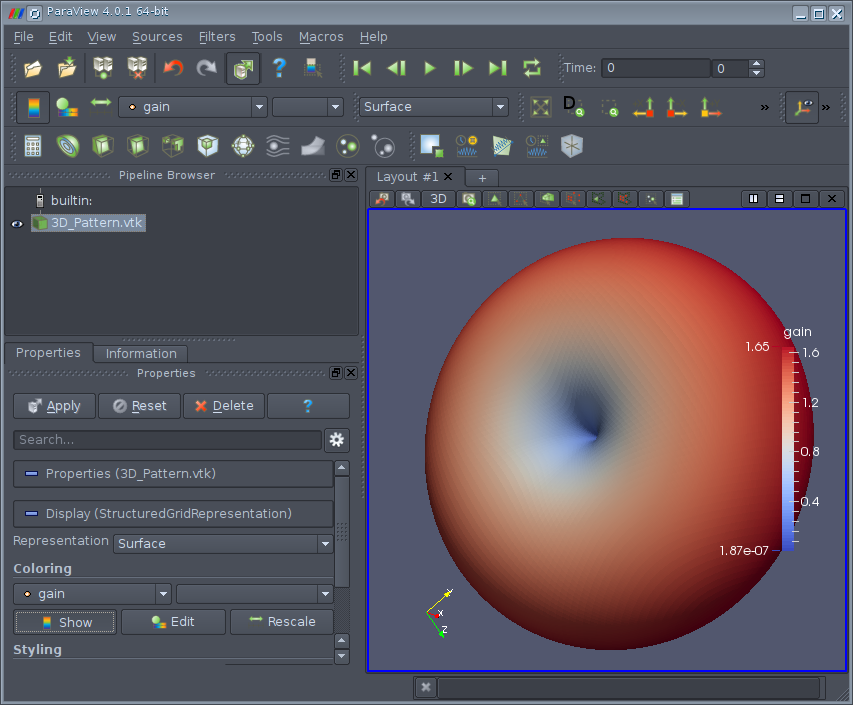
We modeled a dipole antenna in the frequency range from 200 to 600 MHz. As you can see, the simulation gives results close to theory and allows you to take into account the influence of the deviation of the dipole parameters from ideal. Those with HFSS on hand can check the result.

In conclusion, we present our entire script:



Perhaps to be continued ...